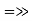Unit - 1
Differentiation
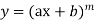
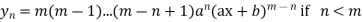
2. If  then
then
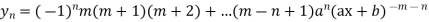

3. If 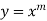 then
then

4. If  then
then 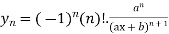
5. If y=log (ax + b) then

6. If  then
then

7. If 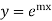 then
then
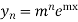
8. If 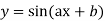 then
then
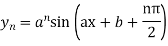
9. If 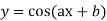 then
then

10. If 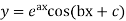 then
then

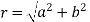

11. If 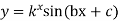 then
then
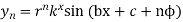
12. If 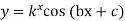 then
then
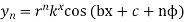
Ques 1 If 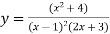 find
find 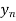 .
.
Let 
Solve by using Partial fraction
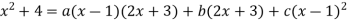
Put x=1 5=5b b=1
Put 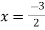
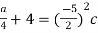
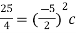 c=1
c=1
Compare the coefficient of  on both sides
on both sides
1=2a+c 1=2a+1 a=0
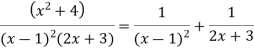
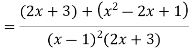
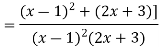

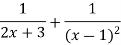
By formula 4 and 2
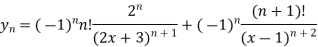
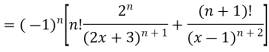
Ques 2 If 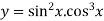 Find
Find 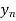
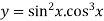
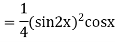
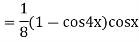
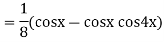
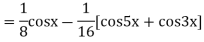
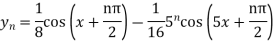
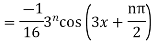
Ques 3 If 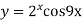 find
find 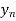
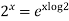
=
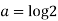
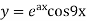
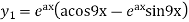
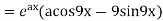

If we put 
Do this calculation by Pythagoras theorem

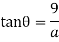
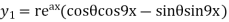

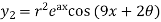
.
.
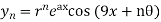
Where 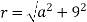
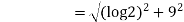 a=log2
a=log2

If y=u.v where u and v are functions of x possessing derivatives of nth order then
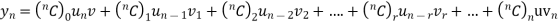
Ques 1 If 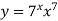 find
find 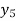
Let u= Formula 6
Formula 6
Now y=uv
By Leibnitz Theorem
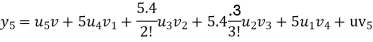
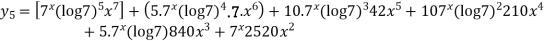
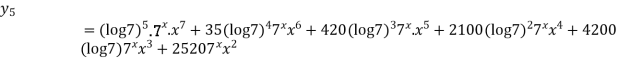
Ques 2 If 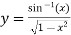 prove that
prove that 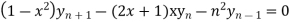
We have 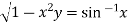
Differentiating w.r.t .x
Applying u.v formula of derivatives

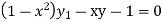
Applying Leibnitz Theorem
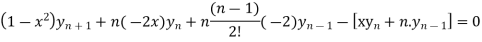
Example 8© If 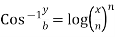 or
or 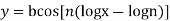 prove that
prove that
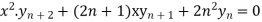
We have 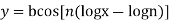


Differentiating again
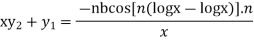
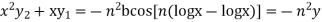

Applying Leibnitz’s Theorem
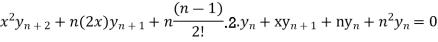
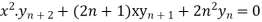
Let f be a real function on a subset of the real numbers and let c be a point in the domain of f. Then/is continuous at c if
lim f(x)= f(c)
More elaborately, if the left hand limit, right hand limit and the value of the function at x — c exist and are equal to each other, i.e.,
lim f(x)= f(c) —— lim f(x)
then f is said to be continuous at x = c.
Continuity in an interval
(i) Its said to be continuous in an open interval (a, b) if it is continuous at every point in this interval.
(ii) Its said to be continuous in the closed interval [a, b] if
f is continuous in (a, b)
 lim /(x) -(a)
lim /(x) -(a)

Geometrical meaning of’ continuity
(iii) Function/ will be continuous at x = c if there is no break in the graph of the function at the point (c, f(c)) .
(iv) In an interval, function is said to be continuous if there is no break in the graph of the function in the entire interval.
(v) The function y —f(x) is said to be differentiable in an open interval (a, b) if it is differentiable at every point of(a, b)
(vi) The function y —f(x) is said to be differentiable in the closed interval [a, b]
if R (a) and L (b) exist and f’ (x) exists for every point of(a, b).
Every differentiable function is continuous, but the converse is not true
Exponential and logarithm functions
(iii) The properties of logarithmic function to any base b > 1 are listed below:

 log, x —— log,. x
log, x —— log,. x
log, b
1
5. log, X ' log, b
1.5 Rolle’s Theorem
Let f: [a, b] —+ R be continuous on [a, b] and differentiable on (a, b), such that f(a)
—f(b), where a and b are some real numbers. Then there exists at least one-point c in (a, b) such that f' (c) = 0.
Example 1 Find the value of the constant k so that the function f defined below is
Continuous at x = 0, where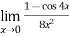 x
x
Solution It is given that the function f is continuous at x = 0. Therefore,


 = k
= k
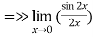 2 =k
2 =k
K=1
Thus f is continuous at x=0 if k=1
Example2: Discuss the continuity of the function x) = sin x . cos x.
Solution: Since sinx and cos x are continuous functions and product of two continuous function is a continuous function, therefore f(x) = sinx . cos x is a continuous function
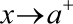 Example 3 Show that the function f defined by
Example 3 Show that the function f defined by
is continuous at x = 0.
Solution Left hand limit at x = 0 is given by
 =
= = 0 { as -1<sin1/x<1}
= 0 { as -1<sin1/x<1}
Similarly  =
=  =0 Moreover f(0)=0
=0 Moreover f(0)=0
Thus 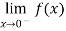 =
= =
= f(0). Hence f is continuous at x=0.
f(0). Hence f is continuous at x=0.
Example 3 Verify Rolle’s theorem for the function, f(x) = sin 2x in (0, )
)
Solution : Consider f(x) = sin 2x in (0, )
)
1) The function f is continuous from (0, ) as f is a sine function, which is always continuous.
) as f is a sine function, which is always continuous.
2) f’(x) =2 cos 2x exist in (0, ), hence f is derivable in (0,
), hence f is derivable in (0, )
)
3) f(0)= sin0 = 0 and f( ) = sin
) = sin 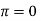 thus f(0)= f(
thus f(0)= f( )
)
Condition of Rolles theorem are satisfied. Hence there is exist at least once c which belongs to (0, ) such that f’(X) =0
) such that f’(X) =0
2cos 2c =0 => 2c= =>c=4
=>c=4
Example 4 Verify mean value theorem for the function f(x) = (x-3) (x-6) (x-9) in [3, 5].
Solution (i) Function/ is continuous in [3, 5] as product of polynomial functions is a polynomial, which is continuous.
(ii) f'(x) = 3x2 36x + 99 exists in (3, 5) and hence derivable in (3, 5).
Thus conditions of mean value theorem are satisfied. Hence, there exists at least one c z (3, 5) such that
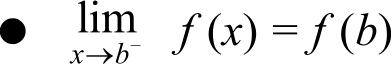
=3c2-36c-99 =8-0/2 =4
C=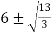
Hence 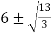 (since other value is not permissible).
(since other value is not permissible).