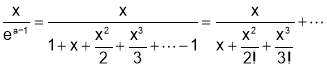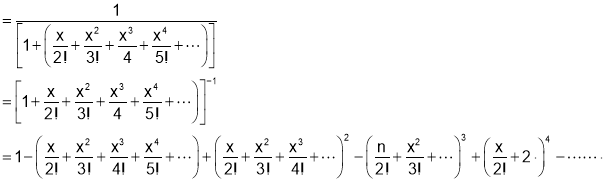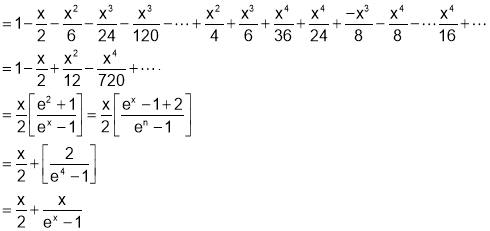Module 2
Limits, homogenous, Maxima Minima
Let f be a function of two variables that is defined in some circular region around (x_0,y_0). The limit of f as x approaches (x_0,y_0) equals L if and only if for every epsilon>0 there exists a delta>0 such that f satisfies

whenever the distance between (x,y) and (x_0,y_0) satisfies

Using limit

when the limit exists. The usual properties of limits hold for functions of two variables: If the following hypotheses hold:
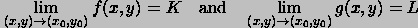
and if c is any real number, then we have the results:
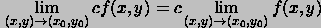

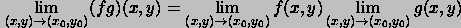

A function f of two variables is continuous at a point (x_0,y_0) if
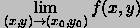

This definition is a direct generalization of the concept of continuity of functions of one variable.
Continuous functions of two variables satisfy all of the usual properties familiar from single variable calculus:
Definition:
Suppose f is a (real valued) function defined on an open interval I and x0 ∈ I. Then f is said to be differentiable at x0 if limx→x0 f(x) − f(x0) x − x0 exists, and in that case the value of the limit is called the derivative of f at x0. The derivative of f at x0, if exists, is denoted by f 0 (x0) or df dx(x0).
Homogenous function:- A function 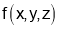 is called a homogenous function of degree n if by putting
is called a homogenous function of degree n if by putting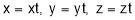 the function
the function 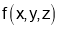 becomes
becomes  i.e.
i.e. 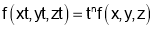
For eg:  is a homogenous function of degree 2 for putting
is a homogenous function of degree 2 for putting 
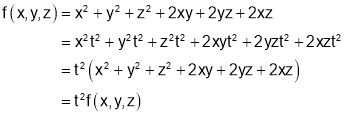
2.4.1 Euler’s Theorem:-
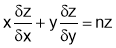
i) Variables x & y of degree n then

ii) If u is a degree n then we can P.T.
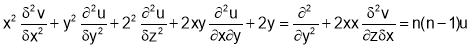
3. If z is homogenous function of degree n is x and y and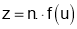 then
then

4. If z is homogenous function of degree n is x and y and z=f(u) then
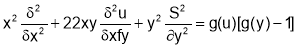
Where 
Q1. If then verify Euler’s theorem for u.
then verify Euler’s theorem for u.
Sol 1. 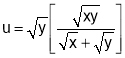

By symmetry,
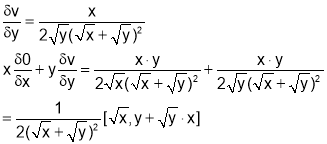
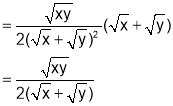
b) Put x=xt, y=yt we get


Thus u is homogenous function of 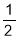
Hence, by Euler’s Theorem
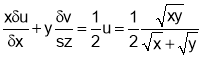
Q2. If  prove that
prove that
Sol 2. Putting x=xt, y=yt we get
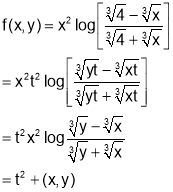
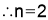
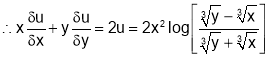
Q3. If 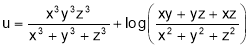 find value of
find value of 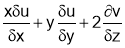
Sol 3. Let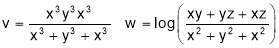
Let u=v+w
Putting x=xt, y=yt, z=zt
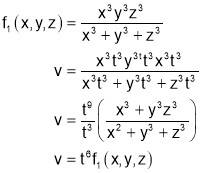
Thus v is homogenous function of degree 6.


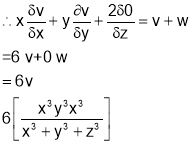
Q4. If 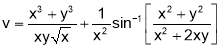 find value
find value  at
at 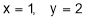
Sol 4. Let 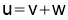
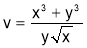
Put 

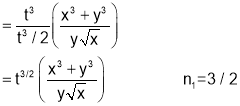
Similarly 
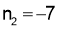
 By Euler’s theorem
By Euler’s theorem
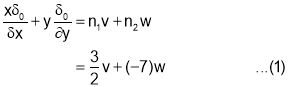
By Euler’s theorem


Adding two result
L.H.S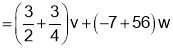
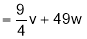
At n=1, y=2


L.H.S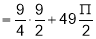
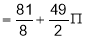
If 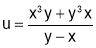 , prove that
, prove that
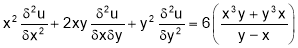
Sol 5. Putting x=xt, y=yt we get
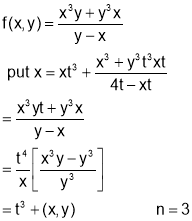
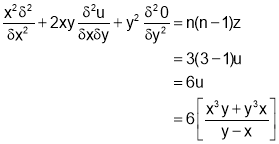
Q5. If  P.T.
P.T. 
Sol 6. 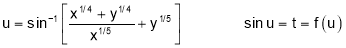
Put x=xt, y=yt

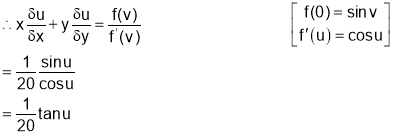
Q6. If  Prove that
Prove that
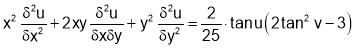
Sol 6. Let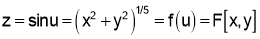
Putting x=xt, y=yt, we get
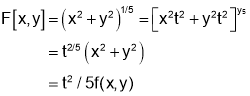
Z=f(u)=sin u is a homogenous function of x,y of degree 2/5

Hence, proved.
Q7. If  Prove that
Prove that

Sol 7. Let 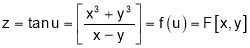
Putting x=xt, y=yt, we get

Thus  is a homogenous function of x, y of degree 2.
is a homogenous function of x, y of degree 2.

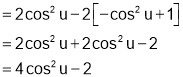
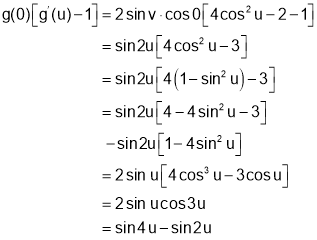
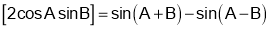
Hence, the required result.

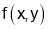

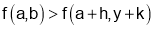
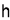
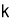
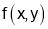
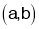
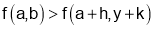
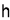
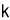
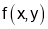
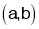

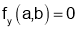
For Maxima or Minima we should have at 
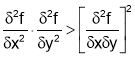
If 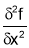 or
or than
than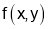 is max at
is max at 
If  or
or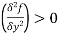 than
than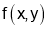 is max at
is max at 
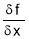
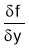
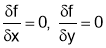

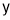
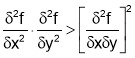
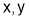
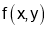
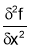
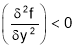
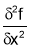
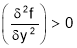
At 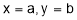 obtained in (ii)
obtained in (ii)
Let us above denote
 ,
,  ,
,
For maxima or minima we must have 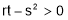
 is maximum if
is maximum if 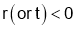
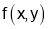 is maximum if
is maximum if 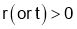
Step 1: Find 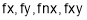 and
and
Step 2: Solve the equation 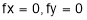
Step 3: Find the value of  at the roots obtained in Step II.
at the roots obtained in Step II.
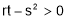
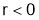
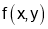
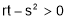
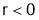

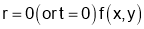
2.5.1 Type 1 Two independent variables: -
Q1. Discuss the maxima and minima of 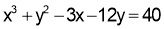 .
.
Sol 1. We have 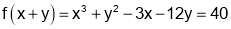
Step 1: 
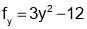
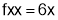

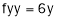
Step 2: 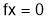
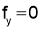
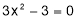

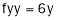
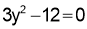
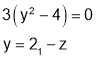
 Stationary Values
Stationary Values 
Step 3:For


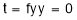
 And
And 
 is a maxima.
is a maxima.
Minimum value
i) For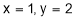

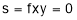


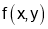 is neither max nor min. It is a saddle point.
is neither max nor min. It is a saddle point.
ii) For
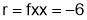

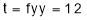

It is neither max nor min. It is a saddle point.
iii) For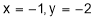
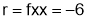

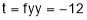
 Add
Add 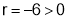
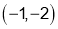 is a maxima.
is a maxima.
Max. value
Example: Find all stationary values of 
Sol: We have 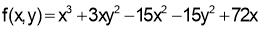
Step I: 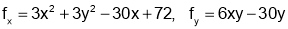
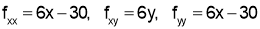
Step II: We now solve 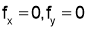
 i.e.
i.e. 
And 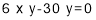

 or
or 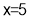
(i) When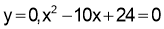
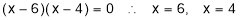
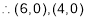 are stationary points.
are stationary points.
(ii) When 
 or
or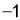 .
.
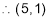 and
and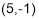 are stationary points.
are stationary points.
Step III: (i) When 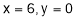
 and
and
 and
and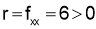
 is minimum at
is minimum at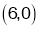 .
.
The minimum value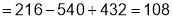 .
.
(ii) When 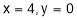

 and
and
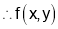 is maximum at
is maximum at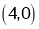 .
.
The maximum value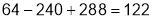
(iii) When

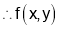 is neither maximum nor minimum.
is neither maximum nor minimum.
(iv) When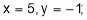
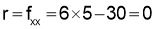
 is neither maximum nor minimum.
is neither maximum nor minimum.
2.5.2 Type II : Three Independent Variable :
Example 1: If  where
where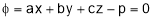 , find the stationary value of u.
, find the stationary value of u.
Sol. : Step I : We have to find the stationary value of
 ………………………(1)
………………………(1)
with the condition that 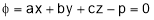 ………………………(2)
………………………(2)
Consider the Lagrange’s function
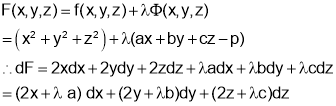
 gives,
gives, 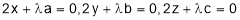 ………………………(3)
………………………(3)
Step II : We have to eliminate x, y, z and 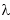 from(1), (2) and (3).
from(1), (2) and (3).
From (3), 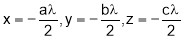 ………………………(4)
………………………(4)
Putting these values in (2),
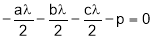

Hence, from(4),

Hence, the stationary value of  is
is
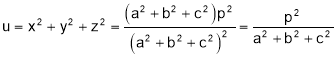
Example 2 : Find the minimum distance from the point  to the cone
to the cone 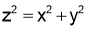
Sol : If 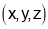 is any point on the cone, its distance from the point
is any point on the cone, its distance from the point 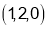 is
is

When the distance is minimum, its square is also minimum.
Step I : We have to find the stationary value of
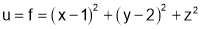 ………………(1)
………………(1)
With the condition that 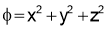 ………………….(2)
………………….(2)
Consider the Lagrange’s function
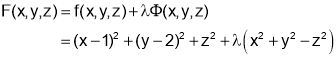
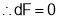 gives
gives
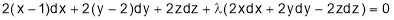
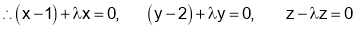 ………………….(3)
………………….(3)
Step II : We have to eliminate x, y, z from (1), (2) and (3).
From (3),
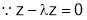
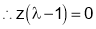

Hence, 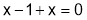
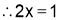
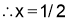

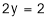

Hence, the required point is  .
.
The distance between 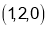 and
and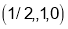 is
is
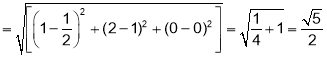
Example 3 : If 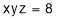 , find the values of x, y, z for which
, find the values of x, y, z for which  is maximum.
is maximum.
Sol. : We have to maximize 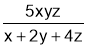 with the condition that
with the condition that 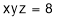 .
.
This means we have to maximize 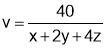
i.e. we have to minimize i.e.
i.e. 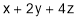
Step I : We have to minimize 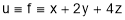 ………………(1)
………………(1)
With the condition that 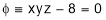 ……………….(2)
……………….(2)
Consider the Lagrange’s function,

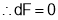 gives
gives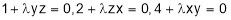
But 
and
In Calculus II you learned Taylor’s Theorem for functions of 1 variable.
Here is one way to state it.
1 of 2: (Taylor’s Theorem, 1 variable) If g is defined on (a, b) and derivatives of order up to m and 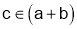 then
then

Where the remainder R satisfies
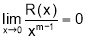
Here is the several variable generalizations of the theorem. I use the following bits of notation in the statement, its specialization to 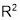 and the sketch of the proof:
and the sketch of the proof:
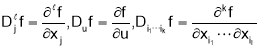
Theorem 2 (Taylor’s Theorem) Suppose U is a convex open set in  and
and  has continuous partial derivatives of all orders up to and including. Fix
has continuous partial derivatives of all orders up to and including. Fix 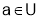 . Then
. Then
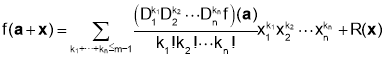
Taking m=4 gives
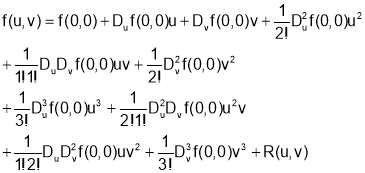
Where
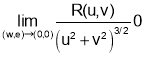
Sketch of proof : Let
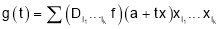
Use the Chain Rule repeatedly to get
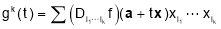
Where the sum is over all ordered k tuples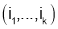 and
and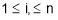 for
for . Now use the one variable Taylor’s Theorem to write
. Now use the one variable Taylor’s Theorem to write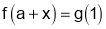 as a polynomial of degree m – 1 in
as a polynomial of degree m – 1 in 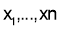 plus a remainder, obtaining
plus a remainder, obtaining



Formulas
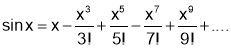

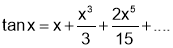
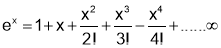
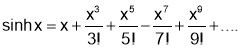
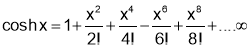
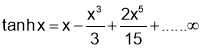
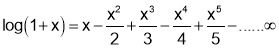
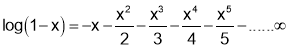

Q1. Prove that 
Sol 1. 

Diff wrt 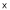
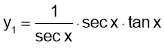


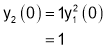
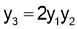


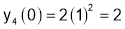
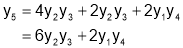
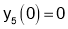
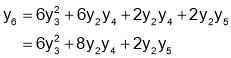
Hence by Maclaurin’s Series
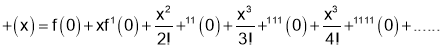 we get
we get
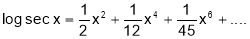
Q2. Show that 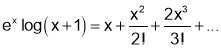
Sol 2. Let 
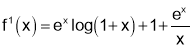 [U.V Value of derivative]
[U.V Value of derivative]
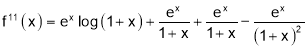
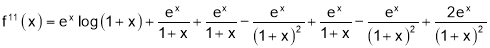
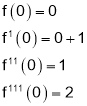
By Maclaurin Series
Q1. Expand  upto
upto 
Sol 1. We have 


Q2. Show that
Sol 2. We have
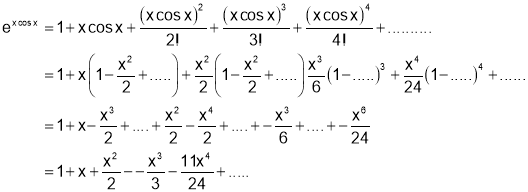
Q3. Prove that 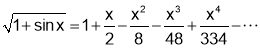
Sol 3. We have

Q4. Expand in Power of 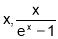
Hence Prove that 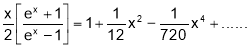
Sol 4.