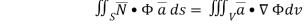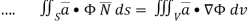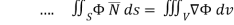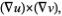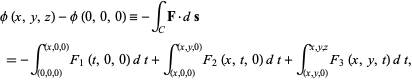Module 3
Vector
If t is a scalar quantity and if to each value of t is an interval there corresponds a vector 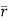 then we say that
then we say that  is a vector function of a scalar variable t and we denote it as
is a vector function of a scalar variable t and we denote it as
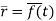
We define a new operator ∇ by
∇=i 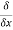 + j
+ j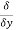 + k
+ k
For a real-valued function f(x,y,z)f(x,y,z) on R3R3, the gradient ∇f(x,y,z)∇f(x,y,z) is a vector-valued function on R3R3 , that is, its value at a point (x,y,z)(x,y,z) is the vector
∇f(x,y,z)=(∂f/∂x,∂f/∂y,∂f/∂z)=∂f/∂xi+∂f/∂yj+∂f/∂zk
For example, it is often convenient to write the divergence div f as ∇⋅f∇⋅f, since for a vector field f(x,y,z)=f1(x,y,z)i+f2(x,y,z)j+f3(x,y,z)kf(x,y,z)=f1(x,y,z)i+f2(x,y,z)j+f3(x,y,z)k, the dot product of f with ∇∇ (thought of as a vector) makes sense:
∇⋅f=(∂/∂xi+∂/∂yj+∂/∂zk)⋅(f1(x,y,z)i+f2(x,y,z)j+f3(x,y,z)k)
=(∂/∂x)(f1)+(∂/∂y)(f2)+(∂/∂z)(f3)
=∂f1/∂x+∂f2/∂y+∂f3/ ∂z
=div f
Let ϕ be a scalar point function and let ϕ(P) and ϕ(Q) be the values of ϕ at two neighbouring points P and Q in the field. Then,
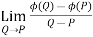

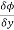 ,
,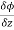 are the directional derivative of ϕ in the direction of the coordinate axes at P.
are the directional derivative of ϕ in the direction of the coordinate axes at P.
The directional derivative of ϕ in the direction l, m, n = l  + m
+ m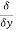 +
+ 
The directional derivative of ϕ in the direction of 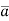 =
= 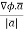
A solenoidal vector field satisfies
∇.B=0 |
|
for every vector  , where
, where 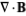 is the divergence. If this condition is satisfied, there exists a vector
is the divergence. If this condition is satisfied, there exists a vector 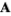 , known as the vector potential, such that
, known as the vector potential, such that
B=∇ X A |
|
where ∇ X A is the curl. This follows from the vector identity
∇. B=∇.(∇ X A) =0 |
|
If A is an irrotational field, then
A x r |
|
is solenoidal. If 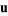 and
and  are irrotational, then
are irrotational, then
U x v |
|
is solenoidal. The quantity
|
|
Where  is the gradient, is always solenoidal. For a function
is the gradient, is always solenoidal. For a function 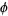 satisfying Laplace's equation
satisfying Laplace's equation
∇2ϕ=0 |
|
it follows that ∇ϕ is solenoidal (and also irrotational).
A vector field 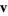 for which the curl vanishes
for which the curl vanishes
A conservative vector field (for which the curl 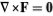 ) may be assigned a scalar potential
) may be assigned a scalar potential
|
where 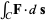 is a line integral.
is a line integral.
Q1. Calculate the curl for the following vector field.
F⃗ =x3y2 i⃗ +x2y3z4 j⃗ +x2z2 k⃗
Solution: In order to calculate the curl, we need to recall the formula.

where P, Q, and R correspond to the components of a given vector field: F⃗ =Pi⃗ +Qj⃗ +Rk⃗
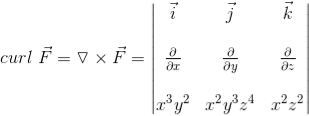
=( (x2z2)−
(x2z2)− (x2y3z4) )i⃗ +(
(x2y3z4) )i⃗ +( (x3y2)−
(x3y2)− (xz2) )j⃗ +(
(xz2) )j⃗ +( (x2y3z4)−
(x2y3z4)− (x3y2) )k⃗
(x3y2) )k⃗
=(0−4x2y3z3)i⃗ +(0−2xz2)j⃗ +(2xy3z4−2x3y)k⃗
Thus the curl is
=(−4x2y3z3)i⃗ +(−2xz2)j⃗ +(2xy3z4−2x3y) k⃗
Q2. Find the directional derivative of Θ=x2y cos z at (1,2,π/2) in the direction of a = 2i+3j+2k.
Solution : ∇ϕ = i 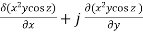 + k
+ k 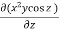
= 2xy cos zi+ x2 cos zj -x2y sin zk
At (1,2,π/2) ∇ϕ = 0i +0j-2k
Directional directive in the direction of 2i+3j+2k.
=(0i+0j-2k). =-
=- 
Q3. In what direction from the point (2,1,-1) is the directional derivative of ϕ=x2yz3 maximum? What is its magnitude?
Solution : ∇ϕ = i 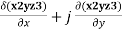 + k
+ k 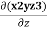
= -4i-4j+12k
Directional derivative is maximum in the direction of ∇Θ. Hence, directional derivative is maximum in the direction of -4i-4j+12k
Its magnitude =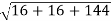 =4
=4
Example 4: Prove that ͞͞͞F = [y2 cos x +z3] i +(2y sin x – 4) j +(3xz2 + 2) k is a conservative field. Find (i) scalar potential for ͞͞͞F (ii) the work done in moving an object in this field from (0, 1, -1) to (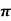 / 2,-1, 2)
/ 2,-1, 2)
 Sol. : (a) The field is conservative if cur ͞͞͞ ͞͞͞F = 0.
Sol. : (a) The field is conservative if cur ͞͞͞ ͞͞͞F = 0.
 Now, cur ͞͞͞F =
Now, cur ͞͞͞F =  ̷̷
̷̷ 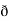 X
X 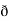 /
/ 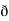 y
y 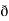 /
/  z
z
i j k
Y2COS X +Z3 2y sin x-4 3xz2 +2
; Cur 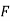 = (0-0) – (3z2 – 3z2) j + (2y cos x- 2y cos x) k = 0
= (0-0) – (3z2 – 3z2) j + (2y cos x- 2y cos x) k = 0
; F is conservative.
(b) Since F is conservative there exists a scalar potential ȸ such that
F = ȸ
 (y2 cos x +z3) i + (2y sin x-4) j + (3xz2 + 2) k
(y2 cos x +z3) i + (2y sin x-4) j + (3xz2 + 2) k
=  i +
i + 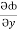 j +
j + 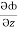 k
k

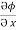 = y2 cos x + z3,
= y2 cos x + z3, 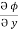 = 2y sin x – 4,
= 2y sin x – 4,  = 3xz2 + 2
= 3xz2 + 2
Now,  =
=  dx +
dx + 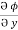 dy +
dy +  dz
dz
= (y2 cos x + z3) dx +(2y sin x – 4)dy + (3xz2 + 2)dz
= (y2 cos x dx + 2y sin x dy) +(z3dx +3xz2 dz) +(- 4 dy) + (2 dz)
=d(y2 sin x + z3x – 4y -2z)
 ȸ = y2 sin x +z3x – 4y -2z
ȸ = y2 sin x +z3x – 4y -2z
(c) now, work done =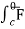 .d ͞r
.d ͞r
= 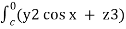 dx + (2y sin x – 4) dy + ( 3xz2 + 2) dz
dx + (2y sin x – 4) dy + ( 3xz2 + 2) dz
=  (y2 sin x + z3x – 4y + 2z) (as shown above)
(y2 sin x + z3x – 4y + 2z) (as shown above)
= [ y2 sin x + z3x – 4y + 2z ]( 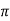 /2, -1, 2)
/2, -1, 2)
= [ 1 +8  + 4 + 4 ] – { - 4 – 2} =4
+ 4 + 4 ] – { - 4 – 2} =4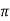 + 15
+ 15
Q5. If 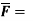 x2zi – 2y3z3j + xy2z2k find dvi
x2zi – 2y3z3j + xy2z2k find dvi 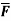 and curl
and curl 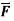 at (1,-1, 1)
at (1,-1, 1)
Solution : div 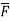 = ∇.
= ∇. =
= 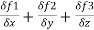 =
=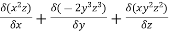
= 2xz – 6y2z3 + 2xy2z =(2-6+2) = -2

 Curl
Curl  =
= 
=i(2xyz2 + 6y3z2) – j(y2z2- x2) + k(0-0)
=-8 at (1,-1,1)
Q6. Find the angle between the normal to the surface xy = z2 at the points (1,4,2) and (-3,-3,3)
Solution: let ϕ = xy-z2
∇ϕ= i 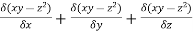 =yi + xj -2zk =4i + j -4k
=yi + xj -2zk =4i + j -4k
∇ϕ = 3i – 3j-6k
But these are the normal to the surface at given points. Angle between two vectors is given by (4i + j -4k).( 4i + j -4k)= |4i + j- 4k|.|-3i-3j -6K|cos θ.
If θ is the angle between then cos θ=  =
= 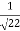 .
.
Let- F be vector function defined throughout some region of space and let C be any curve in that region. ṝ is the position vector of a point p (x,y,z) on C then the integral ƪ F .dṝ is called the line integral of F taken over
Now, since ṝ =xi+yi+zk 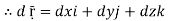
And if F͞ =F1 i + F2 j + F3 K
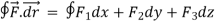
Q1. Evaluate 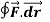 where F= cos y.i-x siny j and C is the curve y=
where F= cos y.i-x siny j and C is the curve y=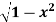 in the xy plae from (1,0) to (0,1)
in the xy plae from (1,0) to (0,1)
Solution : The curve y= i.e x2+y2 =1. Is a circle with centre at the origin and radius unity.
i.e x2+y2 =1. Is a circle with centre at the origin and radius unity.
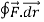 =
= 
= 
=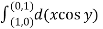 =-1
=-1
Q2. Evaluate 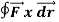 where
where 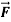 = (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
= (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
Solution : F x dr = 
Put x=t, y=t2, z= t3
Dx=dt , dy=2tdt, dz=3t2dt.
F x dr = 
=(3t4-6t8) dt i – ( 6t5+3t8 -3t7) dt j +( 4t4+2t7-t2)dt k
= t4-6t3)dt i –(6t5+3t8-3t7)dt j+(4t4 + 2t7 – t2)dt k
t4-6t3)dt i –(6t5+3t8-3t7)dt j+(4t4 + 2t7 – t2)dt k
=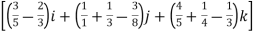
= +
+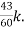
Q3. Prove that ͞͞͞F = [y2 cos x +z3] i +(2y sin x – 4) j +(3xz2 + 2) k is a conservative field. Find (i) scalar potential for ͞͞͞F (ii) the work done in moving an object in this field from (0, 1, -1) to ( / 2,-1, 2)
/ 2,-1, 2)
 Sol. : (a) The field is conservative if cur ͞͞͞ ͞͞͞F = 0.
Sol. : (a) The field is conservative if cur ͞͞͞ ͞͞͞F = 0.
 Now, curl ͞͞͞F =
Now, curl ͞͞͞F =  ̷̷
̷̷  X
X 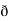 /
/ 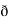 y
y  /
/ 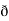 z
z
Y2COS X +Z3 2y sin x-4 3xz2 + 2
; Cur  = (0-0) – (3z2 – 3z2) j + (2y cos x- 2y cos x) k = 0
= (0-0) – (3z2 – 3z2) j + (2y cos x- 2y cos x) k = 0
; F is conservative.
(b) Since F is conservative there exists a scalar potential ȸ such that
F = ȸ
 (y2 cos x=z3) i + (2y sin x-4) j + (3xz2 + 2) k =
(y2 cos x=z3) i + (2y sin x-4) j + (3xz2 + 2) k =  i +
i + 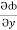 j +
j +  k
k

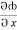 = y2 cos x + z3,
= y2 cos x + z3, 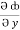 = 2y sin x – 4,
= 2y sin x – 4, 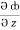 = 3xz2 + 2
= 3xz2 + 2
Now, 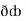 =
= 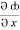 dx +
dx +  dy +
dy + 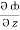 dz
dz
= (y2 cos x + z3) dx +(2y sin x – 4)dy + (3xz2 + 2)dz
= (y2 cos x dx + 2y sin x dy) +(z3dx +3xz2 dz) +(- 4 dy) + (2 dz)
=d(y2 sin x + z3x – 4y -2z)
 ȸ = y2 sin x +z3x – 4y -2z
ȸ = y2 sin x +z3x – 4y -2z
(c) now, work done =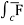 .d ͞r
.d ͞r
= 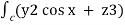 dx + (2y sin x – 4) dy + ( 3xz2 + 2) dz
dx + (2y sin x – 4) dy + ( 3xz2 + 2) dz
=  (y2 sin x + z3x – 4y + 2z) (as shown above)
(y2 sin x + z3x – 4y + 2z) (as shown above)
= [ y2 sin x + z3x – 4y + 2z ](  /2, -1, 2)
/2, -1, 2)
= [ 1 +8  + 4 + 4 ] – { - 4 – 2} =4
+ 4 + 4 ] – { - 4 – 2} =4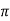 + 15
+ 15
Q1. Find the work done in moving a particle once round the complete circle x2+y2=a2 , z=0 in the force filed given by 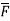 = sin yi +(x + x cos y )j.
= sin yi +(x + x cos y )j.
Solution: work done= 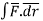 =
= 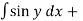 (x+x cos y )dy
(x+x cos y )dy
Using parametric equation x=a cos θ, y=a sinθ
Work done = 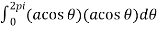
=  .
.
If P and Q are two functions of x, y and their partial derivatives  ,
,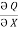 are continuous single valued functions over the closed region bounded by a curve C then
are continuous single valued functions over the closed region bounded by a curve C then
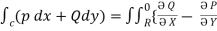 } dx dy.
} dx dy.
EXAMPLE – 1 Verify green’s theorem for 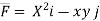 and C is the triangle having verticles A (0,2 ) , B (2,0 ) , C (4,2 ).
and C is the triangle having verticles A (0,2 ) , B (2,0 ) , C (4,2 ).
SOLUTION: By green theorem.

Here , 
(a) Along AB , since the equation of AB is

Putting 

Along BC , since the equation of BC ,  .
.
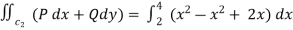
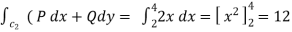
Along CA , since the equation of CA, is y = 2 , dy = 0.

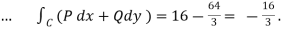
(b) 

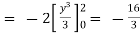 .
.
From (1) and (2) , the theorem is verified .
Example 2: Evaluate by Green ‘s theorem  = - xy (xi –yj) and c is r= a (1+ cos
= - xy (xi –yj) and c is r= a (1+ cos 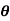 )
)
Sol : By Green’s Theorem , 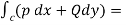
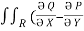 ) dx dy
) dx dy
Now, 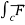 . d ṝ =
. d ṝ =  2 y i + xy2 j ) . (d xi + dy j) =
2 y i + xy2 j ) . (d xi + dy j) =  2y dx + xy2 dy )
2y dx + xy2 dy )
By comparison p= - x2y, Q = xy2

 2,
2, 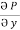 = - x2
= - x2  2 + x2) dx dy
2 + x2) dx dy
To evaluate the integral , we put x = r cos 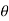 , y = r sin
, y = r sin 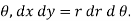 for the cardioid r = a ( 1 + cos
for the cardioid r = a ( 1 + cos 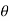 ), we take the integral from
), we take the integral from 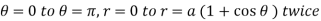
 2 . r dr d
2 . r dr d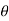 = 2
= 2 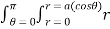 3 dr d
3 dr d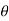
= 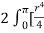 ]a ( 1 + cos
]a ( 1 + cos 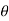 ) dθ =
) dθ = 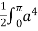 (1+ cos θ)4dθ
(1+ cos θ)4dθ
=8a4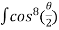 =
= 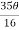 a4
a4
The integral of the normal component of the curl of a vector F͞ over a surface S is equal to the line integral of the tangential component of F͞ around the curve bounding S i.e
 F͞ )ds =
F͞ )ds =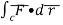
Q1. Use stoke’s theorem to evaluate 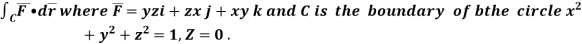
SOLUTION : We have by stoke’s theorem 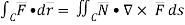
Now , 

The divergence theorem states that the surface integral of the normal component of a vector point function “F” over a closed surface “S” is equal to the volume integral of the divergence of F⃗ taken over the volume “V” enclosed by the surface S. Thus, the divergence theorem is symbolically denoted as:
∬v∫▽F⃗ .dV=∬sF⃗ .n⃗ .dS
Sums on surface and volume
EXAMPLE – 1 Use divergence theorem to show that  where S is any closed surface enclosing a volume V.
where S is any closed surface enclosing a volume V.
SOLUTION: By divergence theorem 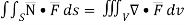
Here , 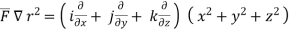
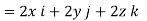

 = 6V
= 6V
EXAMPLE – 2 Show that 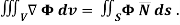
SOLUTION: By divergence theorem, 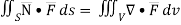 ..…(1)
..…(1)
Comparing this with the given problem let 
Hence, by (1)
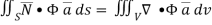 …………. (2)
…………. (2)
Now , 
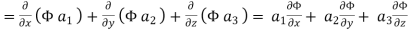

Hence, from (2), We get,