Module 4
First Order Ordinary Differential Equations
A differential equation which is obtained from its primitive by differentiation only and without any operation of elimination and reduction is called an exact differential equation.
Condition: Mdx + Ndy=0 to be exact 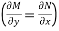
Rule 1: Integrate Mdx w.r.t x treating y constant.
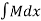 (treating y constant) +
(treating y constant) +  = c
= c
Rule 2 : Integrate N dy wrt y treating constant .
 (treating x constant) +
(treating x constant) +  = c
= c
Example 1:
Solve (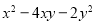 )
)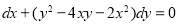
Solution
We have  and
and 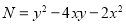
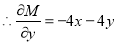 and
and 

Hence, the given equation is exact.
Now, 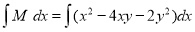

And 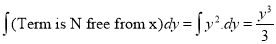
 The Solution is
The Solution is 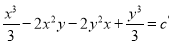
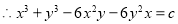
Sometimes a given equation is not exact but is rendered exact if it is multiplied by a suitable factor. If it is called as IF (Integrating Factor).
Equation reducible to exact by IF
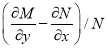
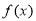

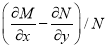
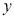
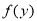
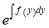
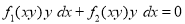
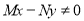
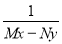
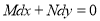
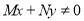
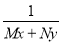
Example 1:
Solve 
Solution:
We have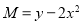 and
and 
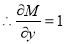 and
and 

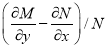 =
=
 I.F.
I.F. 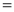
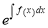
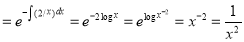
Multiplying by 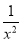 we get
we get 
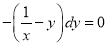 , which is exact.
, which is exact.
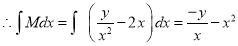
And 

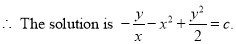
Example 2:
Solve 
Solution:
We have  and
and 

 I.F
I.F 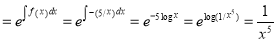
Multiplying the given equation by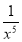 , we get
, we get 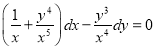
which is exact

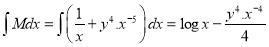
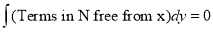
 The solution is
The solution is 
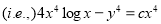
Example 3:
Solve 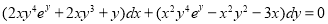
Solution:
We have, 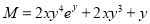
and 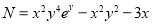
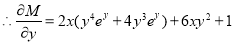
And 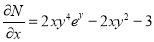
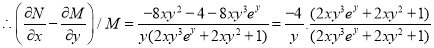
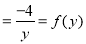
 I.F
I.F 
Multiplying the given equation by I.F, we get
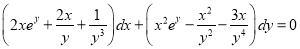 which is exact
which is exact
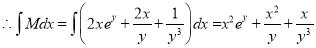

 The solution is
The solution is 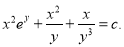
Example 4:
Solve 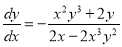
Solution:
The equation can be written as
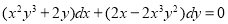

The equation is of the above form and
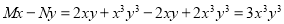
Dividing the equation by 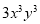 , we get
, we get
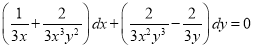
Now, 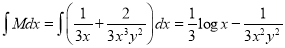
And 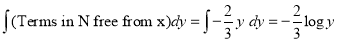
 The solution is
The solution is 

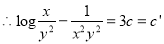
Example 5:
Solve 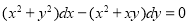
Solution:
The equation is homogeneous and
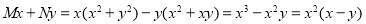
Hence, 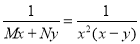 is an integrating factor.
is an integrating factor.
Dividing by 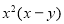 , we get
, we get 
Now this is an exact differential equation.


(By partial fraction treating y constant. Let  )
)
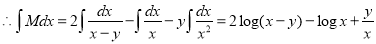
 (Terms in N free from x)
(Terms in N free from x) 

 The solution is
The solution is 
Example 6:
Solve 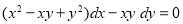
Solution:
The equation is homogeneous and
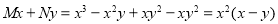
Hence, 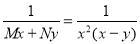 is an integrating factor.
is an integrating factor.
Dividing by 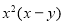 we get
we get 
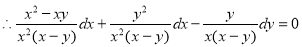
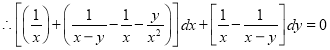
By partial fraction as in (A) of Ex.3 above)
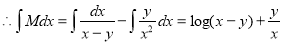
 (Terms in N free from x)
(Terms in N free from x) 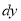

 The solution is
The solution is 
A differential equation is said to be linear if the dependent variable and its derivative appear only in the 1st degree. The form of linear equation of 1st order is

Steps to solve linear equation



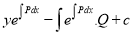
Problem :
Solve 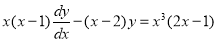
Solution:
Step -1:
Get the equation to the format
Divide the given equation by 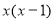 , We get
, We get
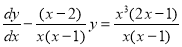

Now,  and
and 
Step – 2:
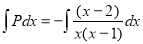
To solve the integrating partial fraction is followed,

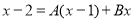
 Put
Put 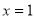 Put
Put 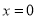
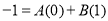

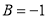

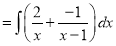
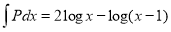

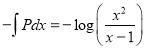
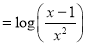
Step – 3:
I.F 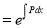


 The solution is
The solution is 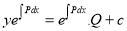
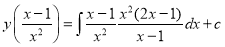
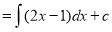

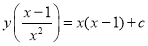
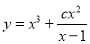
(i) Equation reducible to linear form:
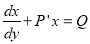
 The solution is
The solution is 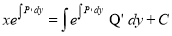
Problem:
Solve 
Solution:
Equation can be written as


 and
and 
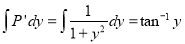
Solution is
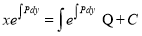
To solve put 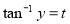
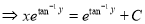
(ii) Equation solvable for y (By substitution)

Step 1: Put 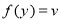
Then 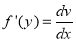
Step 2:
Equation reduces to 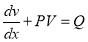 which is linear.
which is linear.
Solution is 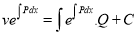
(iii) Equation solvable for x (By substitution)
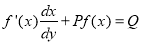
Solution is 
Example :
Solve 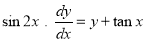
Solution:
The equation can be written as  , which is linear.
, which is linear.
Now, 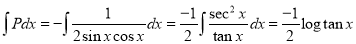

 The solution is
The solution is 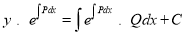

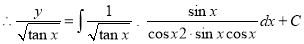

 The solution is
The solution is 
Example :
Solve 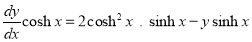
Solution:
We have 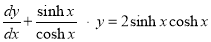
This is linear of the form 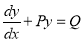
I.F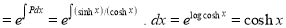
 The solution is
The solution is 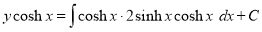
Put 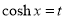
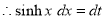

 The solution is
The solution is 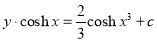
Example :
Solve 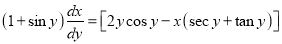
Solution:
The equation can be written as
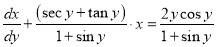
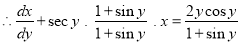
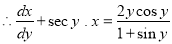
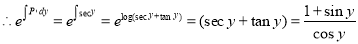
 The solution is
The solution is
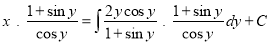

 The solution is
The solution is 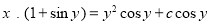
Example :
Solve 
Solution:
This equation can be written as
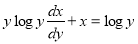
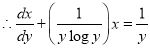
It is of the form 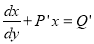
Now,  [Put
[Put 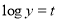 ]
]
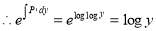
 The solution is
The solution is 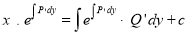
 [Put
[Put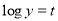 ]
]
Example :
Solve 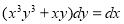
Solution:
The equation can be written as

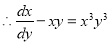
Dividing by  , we get
, we get 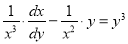
Now put 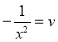
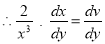
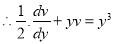
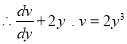
This is linear of the form 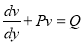
 I.F.
I.F. 
 The solution is
The solution is

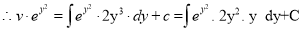
Put  ,
, 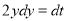 .
.

 The solution is
The solution is 

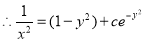
Example:
Solve 
Solution:
The equation can be written as 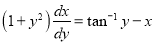
Put 
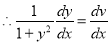
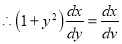

This is a linear differential equation
 I.F
I.F
 The solution is
The solution is 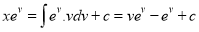 [By parts]
[By parts]
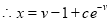
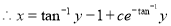 .
.

Step 1: Divide the above equation by ,
,
Step 2:
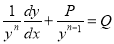
Step 3:
Put 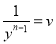
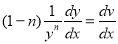

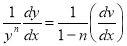
Step 4:
Step 2 becomes
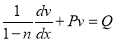

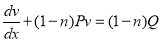
Example:
Solve 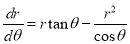 or
or 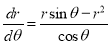
Solution:
The equation can be written as 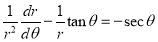
Putting 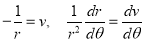

This is a linear equation

 The solution is
The solution is
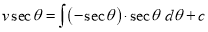



Example:
Solve 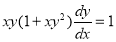
Solution:
We have 
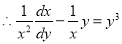
Putting  and
and 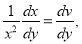 we get
we get 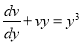
This is a linear differential equation
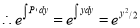
 The solution is
The solution is 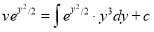
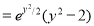

 The solution is
The solution is 
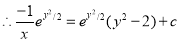
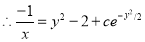

Example:
Solve 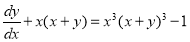
Solution:
Putting 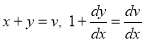 ,
,
The equation then becomes
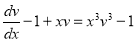
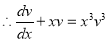
This is a Bernoulli’s equation. Dividing by  throughout, we get
throughout, we get
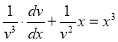
Putting, 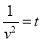 ,
, 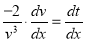 , we get
, we get
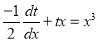
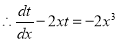
This is a linear equation.
 I.F.
I.F. 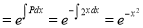
 The solution is
The solution is 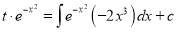
For integration, we put 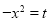 , then
, then 
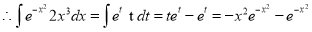
Hence the solution is 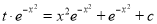
Putting , we get the solution as
, we get the solution as 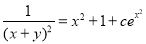
In mathematics, a differential equation of the form y = x (dy/dx) + f(dy/dx) where f(dy/dx) is a function of dy/dx only.
The Clairaut equation has the form:
y=xy′+ψ(y′),
where ψ(y′) is a nonlinear differentiable function. The Clairaut equation is a particular case of the Lagrange equation when φ(y′)=y′. It is solved in the same way by introducing a parameter. The general solution is given by
y=Cx + ψ(C),
where C is an arbitrary constant.
Similarly to the Lagrange equation, the Clairaut equation may have a singular solution that is expressed parametrically in the form:
{x=−ψ′(p)y=xp + ψ(p),
where p is a parameter.
Example 1.
Find the general and singular solutions of the differential equation y=xy′+(y′)2.
Solution.
This is a Clairaut equation. By setting y′=p, we write it in the form
y=xp+p2.
Differentiating in x,, we have
dy=xdp+pdx+2pdp.
Replace dy with pdx to obtain:
pdx=xdp+pdx+2pdp,⇒dp(x+2p)=0.
By equating the first factor to zero, we have
dp=0,⇒p=C.
Now we substitute this into the differential equation:
y=Cx+C2.
Thus, we obtain the general solution of the Clairaut equation, which is an one-parameter family of straight lines.
By equating the second term to zero we find that
x+2p=0,⇒x=−2p.
This gives us the singular solution of the differential equation in parametric form:
{x=−2py=xp+p2.
By eliminating p from this system, we get the equation of the integral curve:
p=−x2,⇒y=x(−x2)+(−x2)2=−x22+x24=−x24.