Module 5
Ordinary Differential Equations of Higher Orders
Let D be symbol which denotes differential with respect to  say of function which immediately follows i.e., D stands for
say of function which immediately follows i.e., D stands for 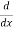


Problem
Solve 
Solution:
Auxiliary equation 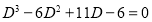

Solution is 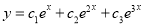
5.1.1 Types of auxiliary equation
If roots are a, a, b

Roots 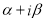
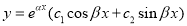
Roots = 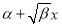
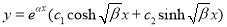
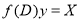
a) Definition: 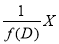 is defined as that function of X which when operated upon by
is defined as that function of X which when operated upon by given X.
given X.
Particular Integral of equation 
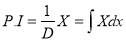
5.1.2 Types of P.I
(i) 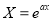

(ii) 

(iii) 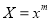
P.I=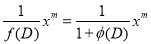
(iv) 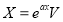

(v) 

(vi) When any of the above method fails to given P.I
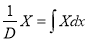

Problem:
Solve 
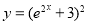
Solution:
Auxiliary equation 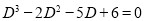
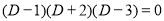
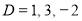
Complementary function 
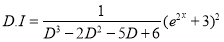
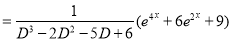
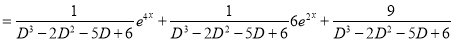
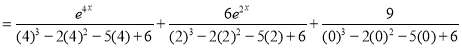

Complete Solution is 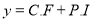
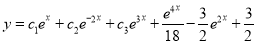
Problem:
Solve 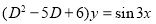
Solution:
Auxiliary equation 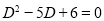
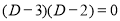

C.F is 
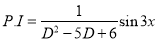
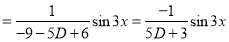
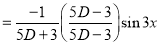
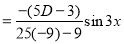
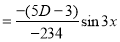
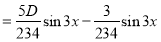
 [
[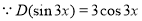 ]
]
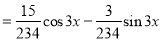
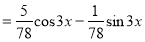
 The Complete Solution is
The Complete Solution is 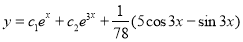
Example
Solve 
Solution:
The Auxiliary equation is 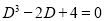
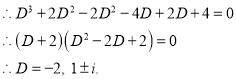
 The C.F is y=
The C.F is y=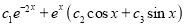
P.I 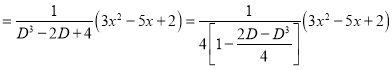
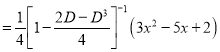
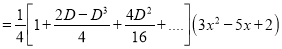
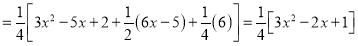
 The Complete Solution is
The Complete Solution is 
Example
Solve 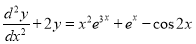
Solution:
The Auxiliary equation is 
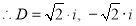
 The C.F is
The C.F is 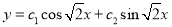
P.I 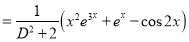
Now, 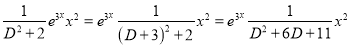
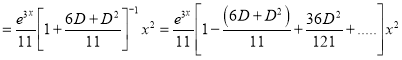
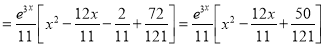


 The Complete Solution is
The Complete Solution is
Example
Solve 
Solution:
The auxiliary solution is 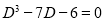
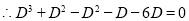
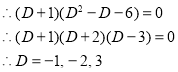
 The C.F is
The C.F is 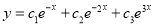

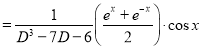
Now, 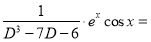
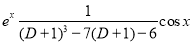

 [Putting
[Putting  ]
]
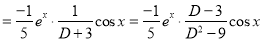

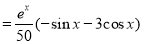
Similarly, we find that
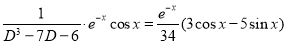
 The Complete Solution is
The Complete Solution is
Example
Solve 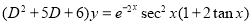
Solution:
The auxiliary equation is 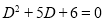

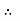 The C.F is
The C.F is 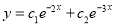
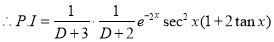
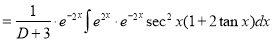 [Put
[Put 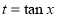 ]
]
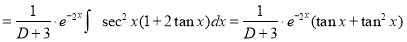
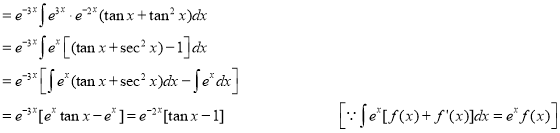
 The Complete Solution is
The Complete Solution is 
Example
Solve 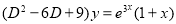
Solution:
The auxiliary equation is 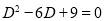

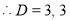
 The C.F is
The C.F is 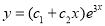

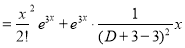
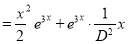
But 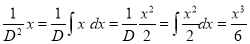
 The Complete Solution is
The Complete Solution is 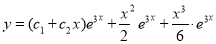
Example
Solve 
Solution:
The auxiliary equation is
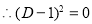
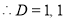
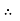 The C.F is
The C.F is 


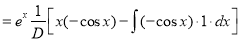 [By parts]
[By parts]

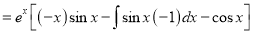

 The Complete Solution is
The Complete Solution is 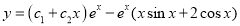
Example
Solve 
Solution:
 The auxiliary equation is
The auxiliary equation is 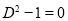
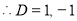
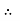 The C.F is
The C.F is 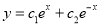
Here 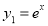 ,
, 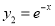 ,
,  . Let
. Let 
Now, 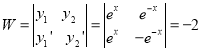
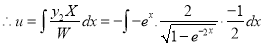
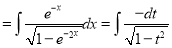 Put
Put 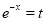


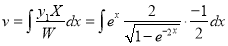
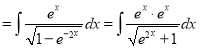
Multiply by 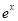 in the numerator and denominator
in the numerator and denominator
Put 
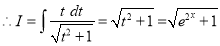


 The Complete Solution is
The Complete Solution is 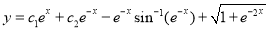
Example
Solve 
Solution:
The auxiliary equation is 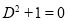
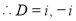
 The C.F is
The C.F is 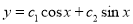
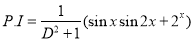
Now, 
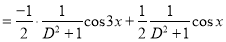

And 
 The Complete Solution
The Complete Solution 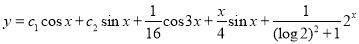
Example
Solve 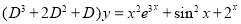
Solution:
The auxiliary equation is 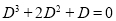


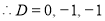
 The C.F is
The C.F is 
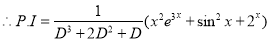
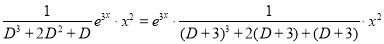
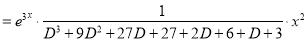
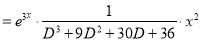
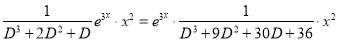
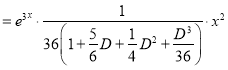

And, 
Now, 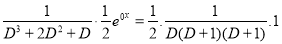
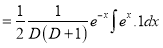

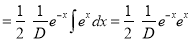

And 
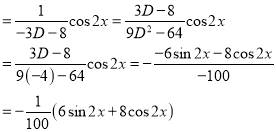
And 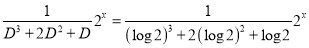
 The Complete Solution is
The Complete Solution is
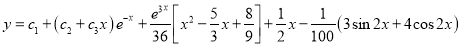
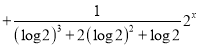
We assume 
Where 
Example:
Apply variation of parameter to solve 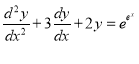
Solution:
Auxiliary equation is 
Solving quadratic equation 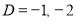
C.F 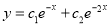
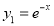
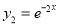
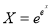
P.I 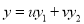
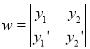

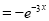
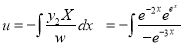
 [Put
[Put  ]
]
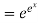

Put 

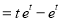
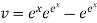

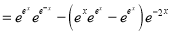

The complete solution is 
The general power series solution method.
 power series represents a function f on an interval of convergence, and that you can successively differentiate the power series to obtain a series for f , f , and so on.
power series represents a function f on an interval of convergence, and that you can successively differentiate the power series to obtain a series for f , f , and so on.
 Example 1 Use a power series to solve the differential equation y - 2y = 0.
Example 1 Use a power series to solve the differential equation y - 2y = 0.
 Solution Assume that y =
Solution Assume that y = 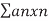 is a solution. Then, y =
is a solution. Then, y =  Substituting
Substituting
 for y’ and -2y, you obtain the following series form of the differential equation.
for y’ and -2y, you obtain the following series form of the differential equation.
 y’ - 2y = 0
y’ - 2y = 0
00
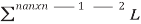 anxn = 0
anxn = 0
n =1
=  2anxn
2anxn
L (n + 1)an +1xn = L 2anxn
n =0 n =0
Now, by equating coefficients of like terms, you obtain the recursion formula
(n + 1)an +1 = 2an, which implies that
Differential Equation which arises in numerous problems, especially in those exhibiting spherical symmetry. Legendre's Differential Equation is defined as:

where 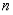 is a real number. The solutions of this equation are called Legendre Functions of degree
is a real number. The solutions of this equation are called Legendre Functions of degree  .
.
When  is a non-negative integer, i.e.,
is a non-negative integer, i.e.,  , the Legendre Functions are often referred to as Legendre Polynomials
, the Legendre Functions are often referred to as Legendre Polynomials  .
.
Since Legendre's differential equation is a second order ordinary differential equation, two sets of functions are needed to form the general solution. Legendre Polynomials of the second kind 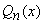 are then introduced. The general solution of a non-negative integer degree Legendre's Differential Equation can hence be expressed as:
are then introduced. The general solution of a non-negative integer degree Legendre's Differential Equation can hence be expressed as:

• 
5.4.1 Functions
Rodrigues' Formula: The Legendre Polynomials 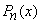 can be expressed by Rodrigues' formula
can be expressed by Rodrigues' formula
 where
where 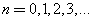
Generating Function: The generating function of a Legendre Polynomial is

Orthogonality: Legendre Polynomials 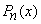 ,
, 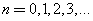 , form a complete orthogonal set on the interval
, form a complete orthogonal set on the interval 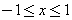 . It can be shown that
. It can be shown that
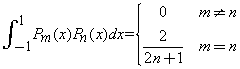
By using this orthogonality, a piecewise continuous function 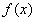 in
in 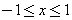 can be expressed in terms of Legendre Polynomials:
can be expressed in terms of Legendre Polynomials:

where:

This orthogonal series expansion is also known as a Fourier-Legendre Series expansion or a Generalized Fourier Series expansion.
Even/Odd Functions: Whether a Legendre Polynomial is an even or odd function depends on its degree 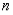 .
.
Based on 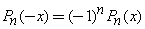 ,
,
• 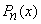 is an even function when
is an even function when 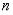 is even.
is even.
• 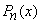 is an odd function when
is an odd function when 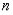 is odd.
is odd.
In addition, from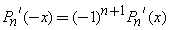 ,
,
• 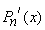 is an even function when
is an even function when 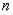 is odd.
is odd.
•  is an odd function when
is an odd function when 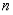 is even.
is even.
Recurrence Relation: A Legendre Polynomial at one point can be expressed by neighbouring Legendre Polynomials at the same point.
• 
• 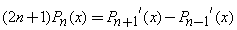
• 
• 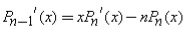
Bessel Differential Equation
The Bessel differential equation is the linear second-order ordinary differential equation given by
|
|
Equivalently, dividing through by 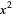 ,
,
|
|
The solutions to this equation define the Bessel functions  and
and 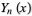 . The equation has a regular singularity at 0 and an irregular singularity at
. The equation has a regular singularity at 0 and an irregular singularity at 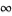 .
.
A transformed version of the Bessel differential equation given by Bowman (1958) is
|
|
The solution is
|
|
where
The solution is
|
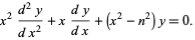
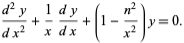
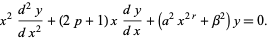
![y=x^(-p)[C_1J_(q/r)(alpha/rx^r)+C_2Y_(q/r)(alpha/rx^r)],](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1648857884_9013994.png)
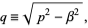
![y={x^alpha[AJ_n(betax^gamma)+BY_n(betax^gamma)] for integer n; x^alpha[AJ_n(betax^gamma)+BJ_(-n)(betax^gamma)] for noninteger n.](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1648857885_0034275.png)