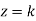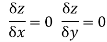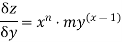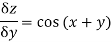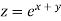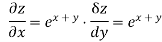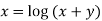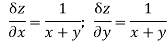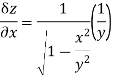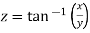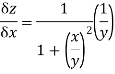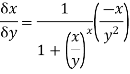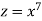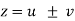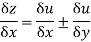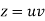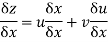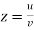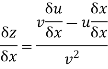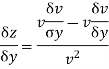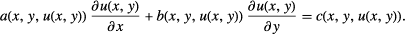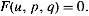Module 6
Partial differentiation
Let  be a function of two independent variable x and y. Suppose now x changes to
be a function of two independent variable x and y. Suppose now x changes to , y remaining constant. Then x will change to
, y remaining constant. Then x will change to 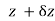 .
.


The limit of 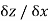 as
as 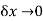 , if it existed is called the partial derivative of z with respect to x and it is denoted by
, if it existed is called the partial derivative of z with respect to x and it is denoted by 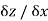 or
or  or
or  .
.
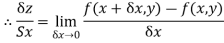
Similarly we can find 

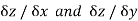
Sol: 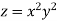
Differentiate z wrt x with y as constant
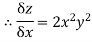
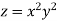
Diff w.r.t y as x as constant
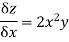
1. | If |
| |
2. | If |
| |
3. | If |
| |
4. | If |
| |
5. | If |
| |
6. | If |
| |
7. | If |
| |
8. | If |
| |
1. | If |
|
2. | If |
|
3. | If |
|
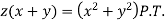
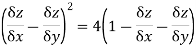
Sol: 
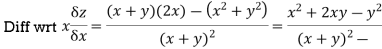
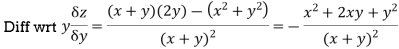
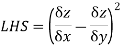

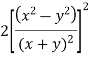
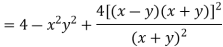
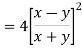
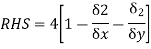

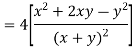

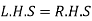
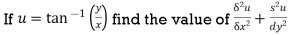
Sol: 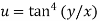



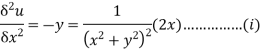
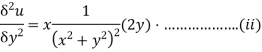

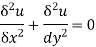
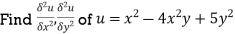
Sol: 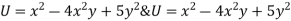
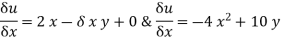
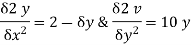
Type II
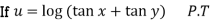

Sol: 
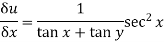


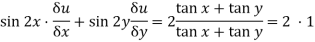
2. Find the value of n , so that  . satifies the equation
. satifies the equation
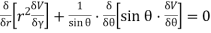
Sol
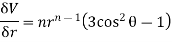

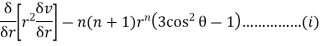
Further diff wrt 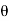
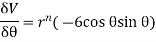
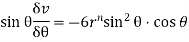
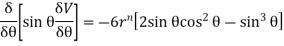

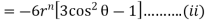
Adding (i) & (ii) we get.
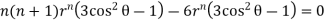
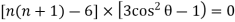
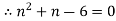
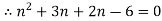


3. 
Sol: 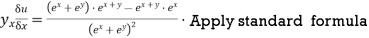
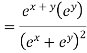
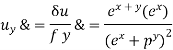
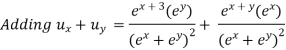
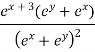

Type III
Q1. 
Sol: 
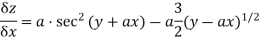
Again diff wrt x
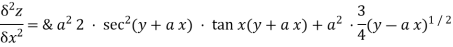
Detailed Explained of the above step

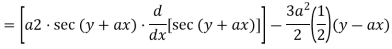
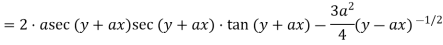
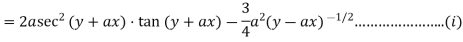
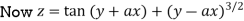

Again differentiating x wrt y
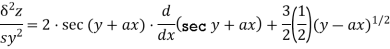
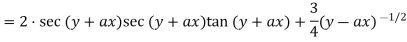
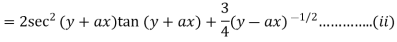
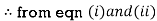
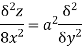
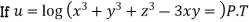
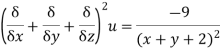
Sol:
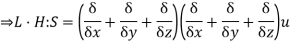

Now
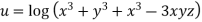
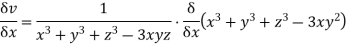
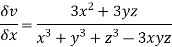
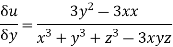
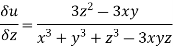
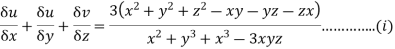
Using the formula
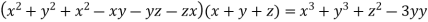
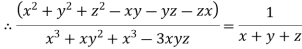
Eq (i) becomes.

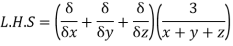


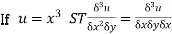
Sol: Since 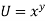 treating y constant
treating y constant
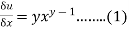
Treating x constant .................(2)
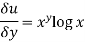
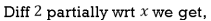
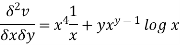
Diff again partially wrt x, we get 
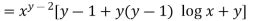

Now diff (1) partially writ y we get.
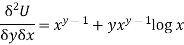
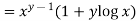
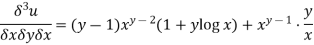
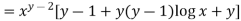
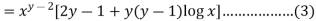

4. 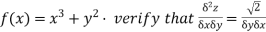
Sol: Differentiating x partially wrt y get,  .
.
Differentiating this paritially wrt x we get.
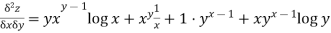
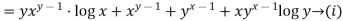
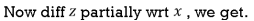

Diff this again partially wrt y we get

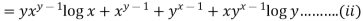

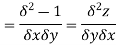
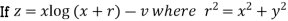
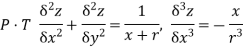
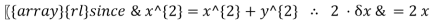
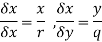


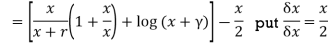

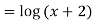
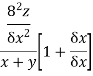
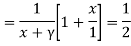
Differentiating  probably
probably
wrt y



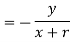


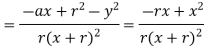
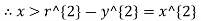
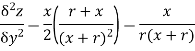
From (i) & (ii)
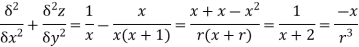
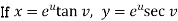
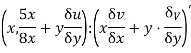
As we want 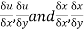 we
we
must express u, v as function 

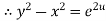
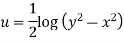


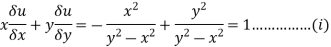



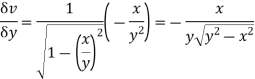


It is given by

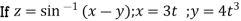
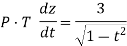
Sol: 

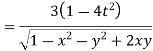
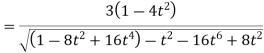
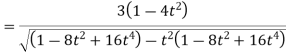
= 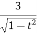
A first-order PDE for an unknown function  is said to be linear if it can be expressed in the form
is said to be linear if it can be expressed in the form
The PDE is said to be quasilinear if it can be expressed in the form
A PDE which is neither linear nor quasi-linear is said to be nonlinear.
The general first-order nonlinear PDE for an unknown function  is given by
is given by
Here 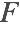 is a function of
is a function of 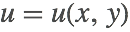 ,
, 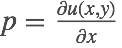 , and
, and 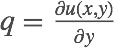 .
.
The term "nonlinear" refers to the fact that 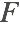 is a nonlinear function of
is a nonlinear function of 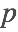 and
and  . For instance, the equation involves a quadratic expression in
. For instance, the equation involves a quadratic expression in 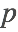 and
and 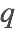 .
.