UNIT 3
Inter-Process Communication
Critical Section is that a part of a program that tries to access shared resources. That resource could also be any resource in an exceedingly pc sort of a memory location, arrangement, mainframe or any IO device.
The vital section cannot be dead by quite one method at a similar time; software system faces the difficulties in permitting and disallowing the processes from coming into the vital section.
The vital section downside is employed to style a group of protocols which may make sure that the Race condition among the processes can ne'er arise.
In order to synchronize the cooperative processes, our main task is to resolve the vital section downside. we want to produce an answer in such the way that the subsequent conditions may be happy.
Requirements of Synchronization mechanisms
Primary
Our resolution should give mutual exclusion. By Mutual Exclusion, we tend to mean that if one method is capital punishment within vital section then the opposite method should not enter within the vital section.
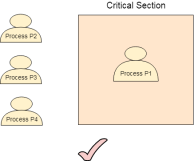
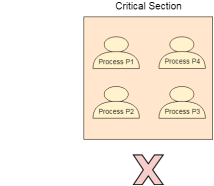
Fig 1 – Critical Section
2. Progress
Progress means if one method does not have to be compelled to execute into vital section then it shouldn't stop different processes to induce into the vital section.
Secondary
We should be ready to predict the waiting time for each method to induce into the vital section. the method should not be endlessly looking ahead to moving into the vital section.
2. branch of knowledge Neutrality
Our mechanism should be branch of knowledge natural. It means if our resolution is functioning fine on one design then it ought to conjointly run on the opposite ones likewise.
Key takeaway
Critical Section is the part of a program which tries to access shared resources. That resource may be any resource in a computer like a memory location, Data structure, CPU or any IO device.
The critical section cannot be executed by more than one process at the same time; operating system faces the difficulties in allowing and disallowing the processes from entering the critical section.
The critical section problem is used to design a set of protocols which can ensure that the Race condition among the processes will never arise.
Race conditions, essential Sections associate degreed Semaphores are a key a part of operational systems. Details concerning these are given as follows −
Race Condition
A race condition may be a state of affairs which will occur within a essential section. This happens once the results of multiple thread execution in essential section differs in keeping with the order within which the threads execute.
Race conditions in essential sections may be avoided if the essential section is treated as associate degree atomic instruction. Also, correct thread synchronization mistreatment locks or atomic variables will stop race conditions.
Critical Section
The essential section during a code phase wherever the shared variables may be accessed. Atomic action is needed during a essential section i.e. only 1 method will execute in its essential section at a time. All the opposite processes have to be compelled to wait to execute in their essential sections.
The essential section is given as follows:
do{
Entry Section
essential Section
Exit Section
Remainder Section
} whereas (TRUE);
In the higher than diagram, the entry sections handles the entry into the essential section. It acquires the resources required for execution by the method. The exit section handles the exit from the essential section. It releases the resources and conjointly informs the opposite processes that essential section is free.
The essential section drawback desires an answer to synchronize the various processes. the answer to the essential section drawback should satisfy the subsequent the subsequent
• Mutual Exclusion
Mutual exclusion implies that only 1 method may be within the essential section at any time. If the other processes need the essential section, they have to wait till it's free.
• Progress
Progress implies that if a method isn't mistreatment the essential section, then it mustn't stop the other method from accessing it. In alternative words, any method will enter a essential section if it's free.
• Bounded Waiting
Bounded waiting implies that every method should have a restricted waiting time. It mustn't wait endlessly to access the essential section.
• Semaphore
A semaphore may be a signaling mechanism and a thread that's waiting on a semaphore may be signaled by another thread. {this is|this is often|this may be} completely different than a mutex because the mutex can be signaled solely by the thread that known as the wait operate.
A semaphore uses 2 atomic operations, wait and signal for method synchronization.
The wait operation decrements the worth of its argument S, if it's positive. If S is negative or zero, then no operation is performed.
wait(S){
whereas (S<=0);
S--;
}
The signal operation increments the worth of its argument S.
signal(S)
Key takeaway
A race condition is a situation that may occur inside a critical section. This happens when the result of multiple thread execution in critical section differs according to the order in which the threads execute.
Race conditions in critical sections can be avoided if the critical section is treated as an atomic instruction. Also, proper thread synchronization using locks or atomic variables can prevent race conditions.
During concurrent execution of processes, processes need to enter the critical section (or the section of the program shared across processes) at times for execution. It might so happen that because of the execution of multiple processes at once, the values stored in the critical section become inconsistent. In other words, the values depend on the sequence of execution of instructions – also known as a race condition. The primary task of process synchronization is to get rid of race conditions while executing the critical section.
This is primarily achieved through mutual exclusion.
Mutual exclusion is a property of process synchronization which states that “no two processes can exist in the critical section at any given point of time”. The term was first coined by Djikstra. Any process synchronization technique being used must satisfy the property of mutual exclusion, without which it would not be possible to get rid of a race condition.
To understand mutual exclusion, let’s take an example.
Example:
In the clothes section of a supermarket, two people are shopping for clothes.
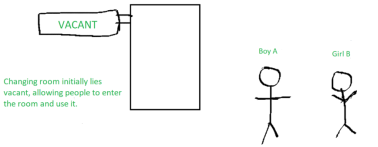
Boy A decides upon some clothes to buy and heads to the changing room to try them out. Now, while boy A is inside the changing room, there is an ‘occupied’ sign on it – indicating that no one else can come in. Girl B has to use the changing room too, so she has to wait till boy A is done using the changing room.
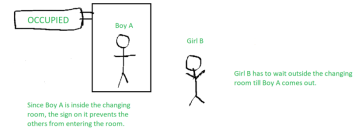
Once boy A comes out of the changing room, the sign on it changes from ‘occupied’ to ‘vacant’ – indicating that another person can use it. Hence, girl B proceeds to use the changing room, while the sign displays ‘occupied’ again.
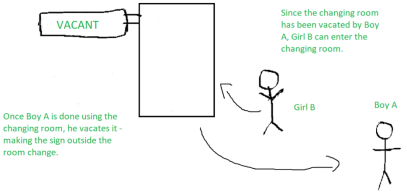
The changing room is nothing but the critical section, boy A and girl B are two different processes, while the sign outside the changing room indicates the process synchronization mechanism being used.
Key takeaway
Mutual exclusion is a property of process synchronization which states that “no two processes can exist in the critical section at any given point of time”. The term was first coined by Djikstra. Any process synchronization technique being used must satisfy the property of mutual exclusion, without which it would not be possible to get rid of a race condition.
In Synchronization hardware, we have a tendency to explore many a lot of solutions to the critical-section downside mistreatment techniques starting from hardware to computer code based mostly Apis accessible to application programmers. These solutions are supported the premise of locking; but, the look of such locks is quite subtle.
These Hardware options will build any programming task easier and improve system potency. Here, we have a tendency to gift some easy hardware directions that are accessible on several systems and show however they'll be used effectively in finding the critical-section downside. If we have a tendency to might forestall interrupts from occurring whereas a shared variable was being changed. The critical-section downside can be resolved merely during a uniprocessor atmosphere. during this manner, we'd be reassuring that the present sequence of directions would be allowed to execute so as while not pre-emption. No different directions would be run; thus, no surprising modifications can be created to the shared variable. this can be the approach taken by non-pre-emptive kernels. however sadly, this resolution isn't as possible during a digital computer atmosphere. Since the message is passed to all or any the processors, disabling interrupts on a digital computer is time intense.
System potency decreases once this massage passing delays entry into every important section. conjointly the impact on a system’s clock is taken into account if the clock is unbroken updated by interrupts. such a large amount of trendy laptop systems so offers special hardware directions that enable USA that we are able to take a look at and modify the content of a word or to swap the contents of 2 words atomically—that is, collectively uninterruptible unit. we have a tendency to could use these special directions to unravel the critical-section downside during a comparatively easy manner. currently we have a tendency to abstract the most ideas behind these sorts of directions. The TestAndSet() instruction is outlined as shown in below code.
boolean take a look at and set(boolean *target)mathematician recreational vehicle = *target;
*target = true;
return rv;
}
Definition of the take a look at and set() instruction.
The essential characteristic is that this instruction is dead atomically. So, if 2 TestAndSet C) directions ar dead at the same time (each on a distinct CPU), they'll be dead consecutive in some absolute order. we are able to implement mutual exclusion by declaring a mathematician variable lock, initialized to false, if the machine supports the TestAndSet () instruction. The structure of method P, is shown in below.
Example
do {
whereas (test and set(&lock)) ;
/* do nothing */
/* important section */
lock = false;
/* remainder section */
}
while (true);
Mutual-exclusion implementation with take a look at and set().
The SwapO instruction, in distinction to the TestAndSet0 instruction, operates on the contents of 2 words; it's dead atomically. mutual exclusion is provided as follows if the machine supports the SwapO instruction. Here, a worldwide mathematician variable lock is said and is initialized to false. to boot, every method encompasses a native mathematician variable key. The structure of method P, is shown in figure below.
int compare_and_swap(int *val, int expected, int new val)temporary worker = *val;
if (*val == expected)
*val = new val;
come back temp;
}
Definition of the compare and swap() instruction.
do{
whereas (compare_and_swap(&lock, 0, 1) != 0) ;
/* do nothing */
/* important section */
lock = 0;
/* remainder section */
}
while (true);
Mutual-exclusion implementation with the compare and swap() instruction.
Since these algorithms satisfy the mutual-exclusion demand, they are doing not satisfy the bounded-waiting demand. In below code, we have a tendency to gift another rule mistreatment the TestAndSet() instruction that satisfies all the critical-section needs.
do{
waiting[i] = true;
key = true;
whereas (waiting[i] && key)
key = take a look at and set(&lock);
waiting[i] = false;
/* important section */
j = (i + 1) nothing n;
whereas ((j != i) && !waiting[j])
j = (j + 1) nothing n;
if (j == i)
lock = false;
else
waiting[j] = false;
/* remainder section */
}
while (true);
Bounded-waiting mutual exclusion with take a look at and set().
The same information structures ar mathematician waiting[n]; mathematician lock; These information structures ar initialized to false. To prove the purpose that the mutual exclusion demand is met, we have a tendency to note that method P; will enter its important section provided that either waiting[i] == false or key -- false. the worth of key will become false provided that the TestAndSet() is dead. the primary method to execute the TestAndSet() can realize key == false; all others should wait. The variable waiting[i] could become false provided that another method leaves its important section; just one waiting [i] is ready to false, maintaining the mutual-exclusion demand.
To prove the purpose that the progress demand is met, we have a tendency to note that the arguments bestowed for mutual exclusion conjointly apply here, since a method exiting the important section either set lock to false or sets waiting[j] to false. each of them enables a method that's waiting to enter its important section to proceed. To prove the purpose that the bounded-waiting demand is met, we have a tendency to note that, once a method leaves its important section, it scans the array waiting within the cyclic ordering (z' + one, i + 2,..., n — 1, 0, ..., i — 1). It designates the primary method during this ordering that's within the entry section (waiting [j] =- true) because the next one to enter the important section.
Any method that waiting to enter its important section can so do thus among n — one turns. sadly for hardware designers, implementing atomic TestAndSet() directions on multiprocessors isn't a trivial task.
Key takeaway
In Synchronization hardware, we explore several more solutions to the critical-section problem using techniques ranging from hardware to software-based APIs available to application programmers. These solutions are based on the premise of locking; however, the design of such locks can be quite sophisticated.
Turn Variable or Strict Alternation Approach is the software mechanism implemented at user mode. It is a busy waiting solution which can be implemented only for two processes. In this approach, A turn variable is used which is actually a lock.
This approach can only be used for only two processes. In general, let the two processes be Pi and Pj. They share a variable called turn variable. The pseudo code of the program can be given as following.
For Process Pi
For Process Pj
The actual problem of the lock variable approach was the fact that the process was entering in the critical section only when the lock variable is 1. More than one process could see the lock variable as 1 at the same time hence the mutual exclusion was not guaranteed there.
This problem is addressed in the turn variable approach. Now, A process can enter in the critical section only in the case when the value of the turn variable equal to the PID of the process.
There are only two values possible for turn variable, i or j. if its value is not i then it will definitely be j or vice versa.
In the entry section, in general, the process Pi will not enter in the critical section until its value is j or the process Pj will not enter in the critical section until its value is i.
Initially, two processes Pi and Pj are available and want to execute into critical section.
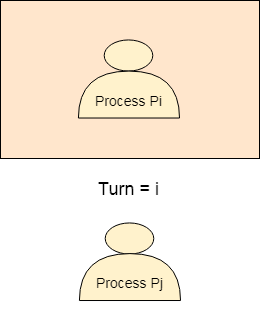
The turn variable is equal to i hence Pi will get the chance to enter into the critical section. The value of Pi remains I until Pi finishes critical section.
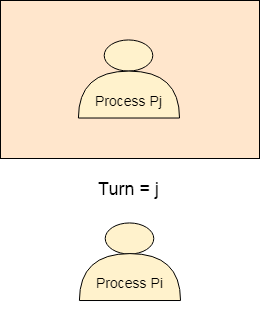
Pi finishes its critical section and assigns j to turn variable. Pj will get the chance to enter into the critical section. The value of turn remains j until Pj finishes its critical section.
Analysis of Strict Alternation approach
Let's analyze Strict Alternation approach on the basis of four requirements.
Mutual Exclusion
The strict alternation approach provides mutual exclusion in every case. This procedure works only for two processes. The pseudo code is different for both of the processes. The process will only enter when it sees that the turn variable is equal to its Process ID otherwise not Hence No process can enter in the critical section regardless of its turn.
Progress
Progress is not guaranteed in this mechanism. If Pi doesn't want to get enter into the critical section on its turn then Pj got blocked for infinite time. Pj has to wait for so long for its turn since the turn variable will remain 0 until Pi assigns it to j.
Portability
The solution provides portability. It is a pure software mechanism implemented at user mode and doesn't need any special instruction from the Operating System.
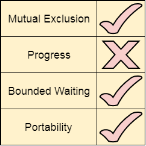
Fig 2 – Process state
Key takeaway
Turn Variable or Strict Alternation Approach is the software mechanism implemented at user mode. It is a busy waiting solution which can be implemented only for two processes. In this approach, A turn variable is used which is actually a lock.
This is a software mechanism implemented at user mode. It is a busy waiting solution can be implemented for only two processes. It uses two variables that are turn variable and interested variable.
The Code of the solution is given below
Till now, each of our solution is affected by one or the other problem. However, the Peterson solution provides you all the necessary requirements such as Mutual Exclusion, Progress, Bounded Waiting and Portability.
Analysis of Peterson Solution
This is a two-process solution. Let us consider two cooperative processes P1 and P2. The entry section and exit section are shown below. Initially, the value of interested variables and turn variable is 0.
Initially process P1 arrives and wants to enter into the critical section. It sets its interested variable to True (instruction line 3) and also sets turn to 1 (line number 4). Since the condition given in line number 5 is completely satisfied by P1 therefore it will enter in the critical section.
Meanwhile, Process P1 got pre-empted and process P2 got scheduled. P2 also wants to enter in the critical section and executes instructions 1, 2, 3 and 4 of entry section. On instruction 5, it got stuck since it doesn't satisfy the condition (value of another interested variable is still true). Therefore, it gets into the busy waiting.
P1 again got scheduled and finish the critical section by executing the instruction no. 6 (setting interested variable to false). Now if P2 checks then it are going to satisfy the condition since other process's interested variable becomes false. P2 will also get enter the critical section.
Any of the process may enter in the critical section for multiple numbers of times. Hence the procedure occurs in the cyclic order.
Mutual Exclusion
The method provides mutual exclusion for sure. In entry section, the while condition involves the criteria for two variables therefore a process cannot enter in the critical section until the other process is interested and the process is the last one to update turn variable.
Progress
An uninterested process will never stop the other interested process from entering in the critical section. If the other process is also interested then the process will wait.
Bounded waiting
The interested variable mechanism failed because it was not providing bounded waiting. However, in Peterson solution, A deadlock can never happen because the process which first sets the turn variable will enter in the critical section for sure. Therefore, if a process is preempted after executing line number 4 of the entry section then it will definitely get into the critical section in its next chance.
Portability
This is the complete software solution and therefore it is portable on every hardware.
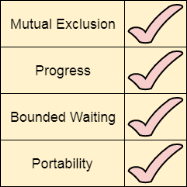
Fig 3 - Process
Key Takeaway
This is a software mechanism implemented at user mode. It is a busy waiting solution can be implemented for only two processes. It uses two variables that are turn variable and interested variable.
The Producer-Consumer problem is a classical multi-process synchronization problem, that is we are trying to achieve synchronization between more than one process.
There is one Producer in the producer-consumer problem, Producer is producing some items, whereas there is one Consumer that is consuming the items produced by the Producer. The same memory buffer is shared by both producers and consumers which is of fixed-size.
The task of the Producer is to produce the item, put it into the memory buffer, and again start producing items. Whereas the task of the Consumer is to consume the item from the memory buffer.
Let's understand what is the problem?
Below are a few points that considered as the problems occur in Producer-Consumer:
Let's see the code for the above problem:
Producer Code
Producer Code
Let's understand above Producer and Consumer code:
Before Starting an explanation of code, first, understand the few terms used in the above code:
If we talk about Producer code first:
--Rp is a register which keeps the value of m[count]
--Rp is incremented (As element has been added to buffer)
--an Incremented value of Rp is stored back to m[count]
Similarly, if we talk about Consumer code next:
--Rc is a register which keeps the value of m[count]
--Rc is decremented (As element has been removed out of buffer)
--the decremented value of Rc is stored back to m[count].
BUFFER


As we can see from Fig: Buffer has total 8 spaces out of which the first 5 are filled, in = 5(pointing next empty position) and out = 0(pointing first filled position).
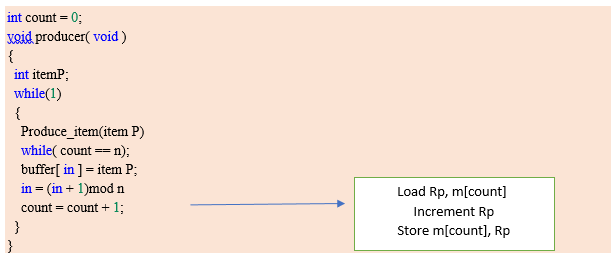
Let's start with the producer who wanted to produce an element " F ", according to code it will enter into the producer() function, while(1) will always be true, itemP = F will be tried to insert into the buffer, before that while(count == n); will evaluate to be False.
Note: Semicolon after while loop will not let the code to go ahead if it turns out to be True (i.e. infinite loop/ Buffer is full)
Buffer[in] = itemP → Buffer[5] = F. ( F is inserted now)
in = (in + 1) mod n → (5 + 1)mod 8→ 6, therefore in = 6; (next empty buffer)
After insertion of F, Buffer looks like this
Where out = 0, but in = 6
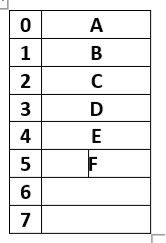
Since count = count + 1; is divided into three parts:
Load Rp, m[count] → will copy count value which is 5 to register Rp.
Increment Rp → will increment Rp to 6.
Suppose just after Increment and before the execution of third line (store m[count], Rp) Context Switch occurs and code jumps to consumer code. . .
Consumer Code:
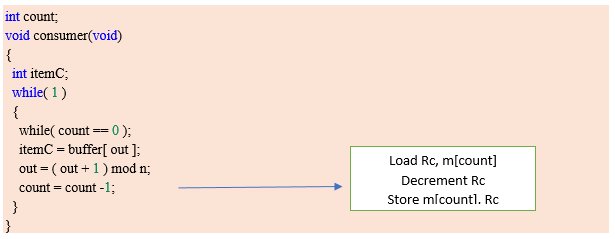
Now starting consumer who wanted to consume the first element " A ", according to code it will enter into the consumer() function, while(1) will always be true, while(count == 0); will evaluate to be False( since the count is still 5, which is not equal to 0.
Note: Semicolon after while loop will not let the code to go ahead if it turns out to be True (i.e. infinite loop/ no element in buffer)
itemC = Buffer[out]→ itemC = A (since out is 0)
out = (out + 1) mod n → (0 + 1) mod 8→ 1, therefore out = 1(first filled position)
A is removed now
After removal of A, Buffer look like this
Where out = 1, and in = 6
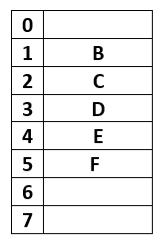
Since count = count - 1; is divided into three parts:
Load Rc, m[count] → will copy count value which is 5 to register Rp.
Decrement Rc → will decrement Rc to 4.
store m[count], Rc → count = 4.
Now the current value of count is 4
Suppose after this Context Switch occurs back to the leftover part of producer code. . .
Since context switch at producer code was occurred after Increment and before the execution of the third line (store m[count], Rp)
So we resume from here since Rp holds 6 as incremented value
Hence store m[count], Rp → count = 6
Now the current value of count is 6, which is wrong as Buffer has only 5 elements, this condition is known as Race Condition and Problem is Producer-Consumer Problem.
The solution of Producer-Consumer Problem using Semaphore
The above problems of Producer and Consumer which occurred due to context switch and producing inconsistent result can be solved with the help of semaphores.
To solve the problem occurred above of race condition, we are going to use Binary Semaphore and Counting Semaphore
Binary Semaphore: In Binary Semaphore, only two processes can compete to enter into its CRITICAL SECTION at any point in time, apart from this the condition of mutual exclusion is also preserved.
Counting Semaphore: In counting semaphore, more than two processes can compete to enter into its CRITICAL SECTION at any point of time apart from this the condition of mutual exclusion is also preserved.
Semaphore: A semaphore is an integer variable in S, that apart from initialization is accessed by only two standard atomic operations - wait and signal, whose definitions are as follows:
From the above definitions of wait, it is clear that if the value of S <= 0 then it will enter into an infinite loop (because of the semicolon; after while loop). Whereas the job of the signal is to increment the value of S.
Let's see the code as a solution of producer and consumer problem using semaphore (Both Binary and Counting Semaphore):
Producer Code- solution
Consumer Code- solution
Let's understand the above Solution of Producer and Consumer code:
Before Starting an explanation of code, first, understand the few terms used in the above code:
If we see the current situation of Buffer
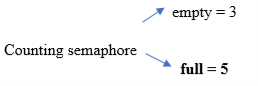
S = 1(init. Value of Binary semaphore
in = 5(next empty buffer)
out = 0(first filled buffer)

As we can see from Fig: Buffer has total 8 spaces out of which the first 5 are filled, in = 5(pointing next empty position) and out = 0(pointing first filled position).
Semaphores used in Producer Code:
6. wait(empty) will decrease the value of the counting semaphore variable empty by 1, that is when the producer produces some element then the value of the space gets automatically decreased by one in the buffer. In case the buffer is full, that is the value of the counting semaphore variable "empty" is 0, then wait(empty); will trap the process (as per definition of wait) and does not allow to go further.
7. wait(S) decreases the binary semaphore variable S to 0 so that no other process which is willing to enter into its critical section is allowed.
8. signal(s) increases the binary semaphore variable S to 1 so that other processes who are willing to enter into its critical section can now be allowed.
9. signal(full) increases the counting semaphore variable full by 1, as on adding the item into the buffer, one space is occupied in the buffer and the variable full must be updated.
Semaphores used in Producer Code:
10.0wait(full) will decrease the value of the counting semaphore variable full by 1, that is when the consumer consumes some element then the value of the full space gets automatically decreased by one in the buffer. In case the buffer is empty, that is the value of the counting semaphore variable full is 0, then wait(full); will trap the process (as per definition of wait) and does not allow to go further.
11. wait(S) decreases the binary semaphore variable S to 0 so that no other process which is willing to enter into its critical section is allowed.
12. signal(S) increases the binary semaphore variable S to 1 so that other processes who are willing to enter into its critical section can now be allowed.
13. signal(empty) increases the counting semaphore variable empty by 1, as on removing an item from the buffer, one space is vacant in the buffer and the variable empty must be updated accordingly.
Producer Code:
Let's start with producer() who wanted to produce an element " F ", according to code it will enter into the producer() function.
wait(empty); will decrease the value of empty by one, i.e. empty = 2
Suppose just after this context switch occurs and jumps to consumer code.
Consumer Code:
Now starting consumer who wanted to consume first element " A ", according to code it will enter into consumer() function,
wait(full); will decrease the value of full by one, i.e. full = 4
wait (S); will decrease the value of S to 0
itemC = Buffer[out]; → itemC = A (since out is 0)
A is removed now
out = (out + 1) mod n → (0 + 1)mod 8 → 1, therefore out = 1( first filled position)
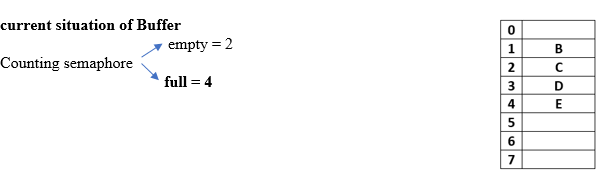
S = 0(Value of Binary semaphore)
in = 5(next empty buffer)
out = 1(first filled buffer)
Suppose just after this context, switch occurs back to producer code
Since the next instruction of producer() is wait(S);, this will trap the producer process, as the current value of S is 0, and wait(0); is an infinite loop: as per the definition of wait, hence producer cannot move further.
Therefore, we move back to the consumer process next instruction.
signal(S); will now increment the value of S to 1.
signal(empty); will increment empty by 1, i.e. empty = 3
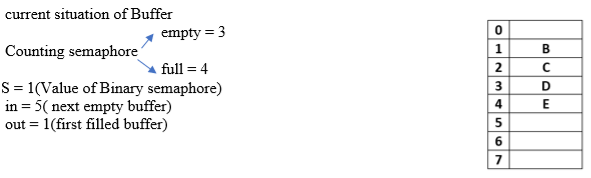
Now moving back to producer() code;
Since the next instruction of producer() is wait(S); will successfully execute, as S is now 1 and it will decrease the value of S by 1, i.e. S = 0
Buffer[in] = itemP; → Buffer[5] = F. ( F is inserted now)
in = (in + 1) mod n → (5 + 1)mod 8 → 6, therefore in = 6; (next empty buffer)
signal(S); will increment S by 1,
signal(full); will increment full by 1, i.e. full = 5
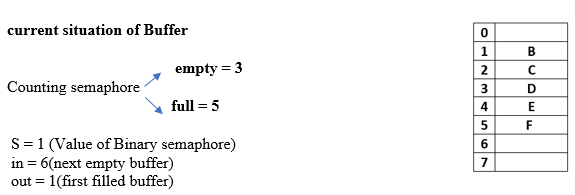
Now add current value of full and empty, i.e. full + empty = 5 + 3 = 8(which is absolutely fine) No inconsistent result is generated even after so many context switches. But in the previous condition of producer and consumer without semaphore, we see the inconsistent result in case of context switches.
This is the solution to the Producer consumer problem.
Key takeaway
The Producer-Consumer problem is a classical multi-process synchronization problem, that is we are trying to achieve synchronization between more than one process.
There is one Producer in the producer-consumer problem, Producer is producing some items, whereas there is one Consumer that is consuming the items produced by the Producer. The same memory buffer is shared by both producers and consumers which is of fixed-size.
The task of the Producer is to produce the item, put it into the memory buffer, and again start producing items. Whereas the task of the Consumer is to consume the item from the memory buffer.
Semaphores are integer variables that are used to solve the critical section problem by using two atomic operations wait and signal that are used for process synchronization.
The definitions of wait and signal are as follows −
The wait operation decrements the value of its argument S, if it is positive. If S is negative or zero, then no operation is performed.
wait(S)
{
while (S<=0);
S--;
}
The signal operation increments the value of its argument S.
signal(S)
{
S++;
}
Types of Semaphores
There are two main types of semaphores i.e. counting semaphores and binary semaphores. Details about these are given as follows −
These are integer value semaphores and have an unrestricted value domain. These semaphores are used to coordinate the resource access, where the semaphore count is the number of available resources. If the resources are added, semaphore count automatically incremented and if the resources are removed, the count is decremented.
The binary semaphores are like counting semaphores but their value is restricted to 0 and 1. The wait operation only works when the semaphore is 1 and the signal operation succeeds when semaphore is 0. It is sometimes easier to implement binary semaphores than counting semaphores.
Advantages of Semaphores
Some of the advantages of semaphores are as follows −
Disadvantages of Semaphores
Some of the disadvantages of semaphores are as follows −
Key takeaway
Semaphores are integer variables that are used to solve the critical section problem by using two atomic operations wait and signal that are used for process synchronization.
Monitors in Operating System
Monitors are used for process synchronization. With the help of programming languages, we can use a monitor to achieve mutual exclusion among the processes. Example of monitors: Java Synchronized methods such as Java offers notify() and wait() constructs.
In other words, monitors are defined as the construct of programming language, which helps in controlling shared data access.
The Monitor is a module or package which encapsulates shared data structure, procedures, and the synchronization between the concurrent procedure invocations.
Characteristics of Monitors
Components of Monitor
There are four main components of the monitor:
Initialization: – Initialization comprises the code, and when the monitors are created, we use this code exactly once.
Private Data: – Private data is another component of the monitor. It comprises all the private data, and the private data contains private procedures that can only be used within the monitor. So, outside the monitor, private data is not visible.
Monitor Procedure: – Monitors Procedures are those procedures that can be called from outside the monitor.
Monitor Entry Queue: – Monitor entry queue is another essential component of the monitor that includes all the threads, which are called procedures.
Syntax of monitor

Condition Variables
There are two types of operations that we can perform on the condition variables of the monitor:
1 2 3 4 |
Suppose there are two condition variables condition a, b // Declaring variable
|
Wait Operation
a.wait(): – The process that performs wait operation on the condition variables are suspended and locate the suspended process in a block queue of that condition variable.
Signal Operation
a.signal() : – If a signal operation is performed by the process on the condition variable, then a chance is provided to one of the blocked processes.
Advantages of Monitor
It makes the parallel programming easy, and if monitors are used, then there is less error-prone as compared to the semaphore.
Difference between Monitors and Semaphore
Monitors | Semaphore |
We can use condition variables only in the monitors. | In semaphore, we can use condition variables anywhere in the program, but we cannot use conditions variables in a semaphore. |
In monitors, wait always block the caller. | In semaphore, wait does not always block the caller. |
The monitors are comprised of the shared variables and the procedures which operate the shared variable. | The semaphore S value means the number of shared resources that are present in the system. |
Condition variables are present in the monitor. | Condition variables are not present in the semaphore. |
Message Passing Model of Process Communication
Process communication is the mechanism provided by the operating system that allows processes to communicate with each other. This communication could involve a process letting another process know that some event has occurred or transferring of data from one process to another. One of the models of process communication is the message passing model.
Message passing model allows multiple processes to read and write data to the message queue without being connected to each other. Messages are stored on the queue until their recipient retrieves them. Message queues are quite useful for inter process communication and are used by most operating systems.
A diagram that demonstrates message passing model of process communication is given as follows −
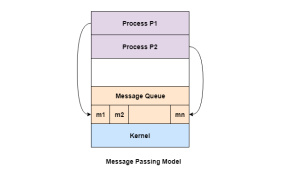
Fig 4 – Message passing model
In the above diagram, both the processes P1 and P2 can access the message queue and store and retrieve data.
Advantages of Message Passing Model
Some of the advantages of message passing model are given as follows −
Disadvantage of Message Passing Model
The message passing model has slower communication than the shared memory model because the connection setup takes time.
Shared Memory Model of Process Communication
Process communication is the mechanism provided by the operating system that allows processes to communicate with each other. This communication could involve a process letting another process know that some event has occurred or transferring of data from one process to another. One of the models of process communication is the shared memory model.
The shared memory in the shared memory model is the memory that can be simultaneously accessed by multiple processes. This is done so that the processes can communicate with each other. All POSIX systems, as well as Windows operating systems use shared memory.
A diagram that illustrates the shared memory model of process communication is given as follows −
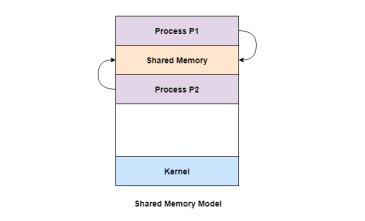
Fig 5 – Shared memory model
In the above diagram, the shared memory can be accessed by Process 1 and Process 2.
Advantage of Shared Memory Model
Memory communication is faster on the shared memory model as compared to the message passing model on the same machine.
Disadvantage of Shared Memory Model
Some of the disadvantages of shared memory model are as follows −
Key takeaway
Monitors are used for process synchronization. With the help of programming languages, we can use a monitor to achieve mutual exclusion among the processes. Example of monitors: Java Synchronized methods such as Java offers notify() and wait() constructs.
In other words, monitors are defined as the construct of programming language, which helps in controlling shared data access.
The Monitor is a module or package which encapsulates shared data structure, procedures, and the synchronization between the concurrent procedure invocations.
READERS WRITERS PROBLEM
The readers-writers problem is a classical problem of process synchronization, it relates to a data set such as a file that is shared between more than one process at a time. Among these various processes, some are Readers - which can only read the data set; they do not perform any updates, some are Writers - can both read and write in the data sets.
The readers-writers problem is used for managing synchronization among various reader and writer process so that there are no problems with the data sets, i.e. no inconsistency is generated.
Let's understand with an example - If two or more than two readers want to access the file at the same point in time there will be no problem. However, in other situations like when two writers or one reader and one writer wants to access the file at the same point of time, there may occur some problems, hence the task is to design the code in such a manner that if one reader is reading then no writer is allowed to update at the same point of time, similarly, if one writer is writing no reader is allowed to read the file at that point of time and if one writer is updating a file other writers should not be allowed to update the file at the same point of time. However, multiple readers can access the object at the same time.
Let us understand the possibility of reading and writing with the table given below:
TABLE 1
Case | Process 1 | Process 2 | Allowed / Not Allowed |
Case 1 | Writing | Writing | Not Allowed |
Case 2 | Reading | Writing | Not Allowed |
Case 3 | Writing | Reading | Not Allowed |
Case 4 | Reading | Reading | Allowed |
The solution of readers and writers can be implemented using binary semaphores.
We use two binary semaphores "write" and "mutex", where binary semaphore can be defined as:
Semaphore: A semaphore is an integer variable in S, that apart from initialization is accessed by only two standard atomic operations - wait and signal, whose definitions are as follows:
From the above definitions of wait, it is clear that if the value of S <= 0 then it will enter into an infinite loop (because of the semicolon; after while loop). Whereas the job of the signal is to increment the value of S.
The below code will provide the solution of the reader-writer problem, reader and writer process codes are given as follows -
Code for Reader Process
The code of the reader process is given below -
In the above code of reader, mutex and write are semaphores that have an initial value of 1, whereas the read count variable has an initial value as 0. Both mutex and write are common in reader and writer process code, semaphore mutex ensures mutual exclusion and semaphore write handles the writing mechanism.
The read count variable denotes the number of readers accessing the file concurrently. The moment variable read count becomes 1, wait operation is used to write semaphore which decreases the value by one. This means that a writer is not allowed how to access the file anymore. On completion of the read operation, read count is decremented by one. When read count becomes 0, the signal operation which is used to write permits a writer to access the file.
Code for Writer Process
The code that defines the writer process is given below:
If a writer wishes to access the file, wait operation is performed on write semaphore, which decrements write to 0 and no other writer can access the file. On completion of the writing job by the writer who was accessing the file, the signal operation is performed on write.
Let's see the proof of each case mentioned in Table 1
CASE 1: WRITING - WRITING → NOT ALLOWED. That is when two or more than two processes are willing to write, then it is not allowed. Let us see that our code is working accordingly or not?
CASE 2: READING - WRITING → NOT ALLOWED. That is when one or more than one process is reading the file, then writing by another process is not allowed. Let us see that our code is working accordingly or not?
CASE 3: WRITING -- READING → NOT ALLOWED. That is when if one process is writing into the file, then reading by another process is not allowed. Let us see that our code is working accordingly or not?
CASE 4: READING - READING → ALLOWED. That is when one process is reading the file, and other process or processes is willing to read, then they all are allowed i.e. reading - reading is not mutually exclusive. Let us see that our code is working accordingly or not?
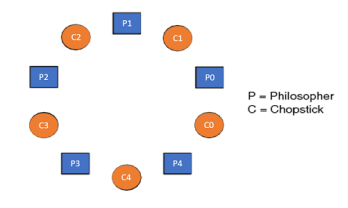
THE DINING PHILOSOPHERS PROBLEM
The dining philosopher's problem is the classical problem of synchronization which says that Five philosophers are sitting around a circular table and their job is to think and eat alternatively. A bowl of noodles is placed at the center of the table along with five chopsticks for each of the philosophers. To eat a philosopher needs both their right and a left chopstick. A philosopher can only eat if both immediate left and right chopsticks of the philosopher is available. In case if both immediate left and right chopsticks of the philosopher are not available then the philosopher puts down their (either left or right) chopstick and starts thinking again.
The dining philosopher demonstrates a large class of concurrency control problems hence it's a classic synchronization problem.

Fig 6 - Five Philosophers sitting around the table
Dining Philosophers Problem- Let's understand the Dining Philosophers Problem with the below code, we have used fig 1 as a reference to make you understand the problem exactly. The five Philosophers are represented as P0, P1, P2, P3, and P4 and five chopsticks by C0, C1, C2, C3, and C4.
Let's discuss the above code:
Suppose Philosopher P0 wants to eat, it will enter in Philosopher() function, and execute take_chopstick[i]; by doing this it holds C0 chopstick after that it execute take_chopstick[ (i+1) % 5]; by doing this it holds C1 chopstick( since i =0, therefore (0 + 1) % 5 = 1)
Similarly suppose now Philosopher P1 wants to eat, it will enter in Philosopher() function, and execute take_chopstick[i]; by doing this it holds C1 chopstick after that it execute take_chopstick[ (i+1) % 5]; by doing this it holds C2 chopstick( since i =1, therefore (1 + 1) % 5 = 2)
But Practically Chopstick C1 is not available as it has already been taken by philosopher P0, hence the above code generates problems and produces race condition.
The solution of the Dining Philosophers Problem
We use a semaphore to represent a chopstick and this truly acts as a solution of the Dining Philosophers Problem. Wait and Signal operations will be used for the solution of the Dining Philosophers Problem, for picking a chopstick wait operation can be executed while for releasing a chopstick signal semaphore can be executed.
Semaphore: A semaphore is an integer variable in S, that apart from initialization is accessed by only two standard atomic operations - wait and signal, whose definitions are as follows:
From the above definitions of wait, it is clear that if the value of S <= 0 then it will enter into an infinite loop (because of the semicolon; after while loop). Whereas the job of the signal is to increment the value of S.
The structure of the chopstick is an array of a semaphore which is represented as shown below -
Initially, each element of the semaphore C0, C1, C2, C3, and C4 are initialized to 1 as the chopsticks are on the table and not picked up by any of the philosophers.
Let's modify the above code of the Dining Philosopher Problem by using semaphore operations wait and signal, the desired code looks like
In the above code, first wait operation is performed on take_chopstickC[i] and take_chopstickC [ (i+1) % 5]. This shows philosopher i have picked up the chopsticks from its left and right. The eating function is performed after that.
On completion of eating by philosopher i the, signal operation is performed on take_chopstickC[i] and take_chopstickC [ (i+1) % 5]. This shows that the philosopher i have eaten and put down both the left and right chopsticks. Finally, the philosopher starts thinking again.
Let's understand how the above code is giving a solution to the dining philosopher problem?
Let value of i = 0( initial value ), Suppose Philosopher P0 wants to eat, it will enter in Philosopher() function, and execute Wait( take_chopstickC[i] ); by doing this it holds C0 chopstick and reduces semaphore C0 to 0, after that it execute Wait( take_chopstickC[(i+1) % 5] ); by doing this it holds C1 chopstick( since i =0, therefore (0 + 1) % 5 = 1) and reduces semaphore C1 to 0
Similarly, suppose now Philosopher P1 wants to eat, it will enter in Philosopher() function, and execute Wait( take_chopstickC[i] ); by doing this it will try to hold C1 chopstick but will not be able to do that, since the value of semaphore C1 has already been set to 0 by philosopher P0, therefore it will enter into an infinite loop because of which philosopher P1 will not be able to pick chopstick C1 whereas if Philosopher P2 wants to eat, it will enter in Philosopher() function, and execute Wait( take_chopstickC[i] ); by doing this it holds C2 chopstick and reduces semaphore C2 to 0, after that, it executes Wait( take_chopstickC[(i+1) % 5] ); by doing this it holds C3 chopstick( since i =2, therefore (2 + 1) % 5 = 3) and reduces semaphore C3 to 0.
Hence the above code is providing a solution to the dining philosopher problem, A philosopher can only eat if both immediate left and right chopsticks of the philosopher are available else philosopher needs to wait. Also at one go two independent philosophers can eat simultaneously (i.e., philosopher P0 and P2, P1 and P3 & P2 and P4 can eat simultaneously as all are the independent processes and they are following the above constraint of dining philosopher problem)
The drawback of the above solution of the dining philosopher problem
From the above solution of the dining philosopher problem, we have proved that no two neighbouring philosophers can eat at the same point in time. The drawback of the above solution is that this solution can lead to a deadlock condition. This situation happens if all the philosophers pick their left chopstick at the same time, which leads to the condition of deadlock and none of the philosophers can eat.
To avoid deadlock, some of the solutions are as follows -
The design of the problem was to illustrate the challenges of avoiding deadlock, a deadlock state of a system is a state in which no progress of system is possible. Consider a proposal where each philosopher is instructed to behave as follows:
Key takeaway
The readers-writers problem is a classical problem of process synchronization, it relates to a data set such as a file that is shared between more than one process at a time. Among these various processes, some are Readers - which can only read the data set; they do not perform any updates, some are Writers - can both read and write in the data sets.
The readers-writers problem is used for managing synchronization among various reader and writer process so that there are no problems with the data sets, i.e. no inconsistency is generated.
References