Unit - 1
Introduction
Phases of compilation -
The method of compilation includes the sequence of different stages. Each phase takes a source programme in one representation and produces output in another representation. From its previous stage, each process takes input.
The various stages of the compiler take place:
- Lexical Analysis
- Syntax Analysis
- Semantic Analysis
- Intermediate Code Generation
- Code Optimization
- Code Generation
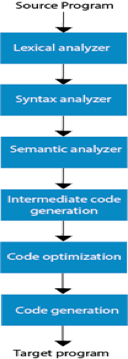
Fig 1: phases of compiler
- Lexical Analysis: The first phase of the compilation process is the lexical analyzer phase. As input, it takes source code. One character at a time, it reads the source programme and translates it into meaningful lexemes. These lexemes are interpreted in the form of tokens by the Lexical analyzer.
- Syntax Analysis: Syntax analysis is the second step of the method of compilation. Tokens are required as input and a parse tree is generated as output. The parser verifies that the expression made by the tokens is syntactically right or not in the syntax analysis process.
- Semantic Analysis: The third step of the method of compilation is semantic analysis. This tests whether the parse tree complies with language rules. The semantic analyzer keeps track of identifiers, forms, and expressions of identifiers. The output step of semantic analysis is the syntax of the annotated tree.
- Intermediate Code Generation: The compiler generates the source code into an intermediate code during the intermediate code generation process. Between high-level language and machine language, intermediate code is created. You can produce the intermediate code in such a way that you can convert it easily into the code of the target computer.
- Code Optimization: An optional step is code optimization. It is used to enhance the intermediate code so that the program's output can run quicker and take up less space. It eliminates redundant code lines and arranges the sequence of statements to speed up the execution of the programme.
- Code Generation: The final stage of the compilation process is code generation. It takes as its input the optimised intermediate code and maps it to the language of the target computer. The code generator converts the intermediate code to the required computer's machine code.
Overview
● A compiler is a translator that translates the language at the highest level into the language of the computer.
● A developer writes high-level language and the processor can understand machine language.
● The compiler is used to display a programmer's errors.
● The main objective of the compiler is to modify the code written in one language without altering the program's meaning.
● When you run a programme that is written in the language of HLL programming, it runs in two parts.
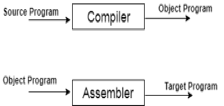
Fig 2: Execution process of Compiler
Features of compilers:
● Maintaining the right interpretation of the code
● The speed of the target code
● Understand prototypes for legal and illegal systems
● Good documentation / management of errors
● Correctness
● Speed of compilation
● Code debugging help
Task of compilers:
Tasks which are performed by compilers:
● Divides the source program into parts and imposes on them a grammatical structure.
● Allows you from the intermediate representation to construct the desired.
● target program and also create the symbol table.
● Compiles and detects source code errors.
● Storage of all variables and codes is handled.
● Separate compilation support.
● Learn, interpret, and translate the entire program to a semantically equivalent.
● Depending on the computer sort, conversion of the source code into object code.
Key takeaway:
● Each phase takes a source programme in one representation and produces output in another representation.
● The method of compilation includes the sequence of different stages.
● A compiler is a computer programme that lets you convert source code into low-level machine language written in a high-level language.
● Without modifying the context of the code, it converts the code written in one programming language to some other language.
● The compiler also makes the end code, optimised for execution time and memory space, efficient.
A language is regular if, in terms of regular expression, it can be presented.
Regular languages are closed under a wide variety of operations.
● Union and intersection
Pick DFAs recognizing the two languages and use the cross-product construction to build a DFA recognizing their union or intersection.
● Set complement
Pick a DFA recognizing the language, then swap the accept/non- accept markings on its states.
● String reversal
Pick an NFA recognizing the language. Create a new final state, with epsilon transitions to it from all the old final states. Then swap the final and start states and reverse all the transition arrows.
● Set difference
Rewrite set difference using a combination of intersection and set complement.
● Concatenation and Star
Pick an NFA recognizing the language and modify.
● Homomorphism
A homomorphism is a function from strings to strings. What makes it a homomorphism is that its output on a multi-character string is just the concatenation of its outputs on each individual character in the string. Or, equivalently, h(xy) = h(x)h(y) for any strings x and y. If S is a set of strings, then h(S) is {w : w = h(x) for some x in S}.
To show that regular languages are closed under homomorphism, choose an arbitrary regular language L and a homomorphism h. It can be represented using a regular expression R. But then h(R) is a regular expression representing h(L). So h(L) must also be regular.
Notice that regular languages are not closed under the subset/superset relation. For example, 0 * 1 * is regular, but its subset {O n 1 n : n >= 0} is not regular, but its subset {01, 0011, 000111} is regular again.
● To identify patterns, finite state machines are used.
● The Finite Automated System takes the symbol string as an input and modifies its state accordingly. When a desired symbol is found in the input, then the transformation happens.
● The automated devices may either switch to the next state during the transition or remain in the same state.
● FA has two states: state approve or state deny. When the input string is processed successfully and the automatic has reached its final state, it will approve it.
The following refers of a finite automatic:
Q: finite set of states
∑: finite set of input symbol
q0: initial state
F: final state
δ: Transition function
It is possible to describe transition functions as
δ: Q x ∑ →Q
The FA is described in two ways:
- DFA
- NDFA
DFA
DFA stands for Deterministic Finite Automata .Deterministic refers to computational uniqueness. In DFA, the character of the input goes to only one state. The DFA does not allow the null shift, which means that without an input character, the DFA does not change the state.
DFA has five tuples {Q, ∑, q0, F, δ}
Q: set of all states
∑: finite set of input symbol where δ: Q x ∑ →Q
q0: initial state
F: final state
δ: Transition function
NDFA
NDFA applies to Finite Non-Deterministic Automata. It is used for a single input to pass through any number of states. NDFA embraces the NULL step, indicating that without reading the symbols, it can change the state.
Like the DFA, NDFA also has five states. NDFA, however, has distinct transformation features.
NDFA's transition role may be described as:
δ: Q x ∑ →2Q
Key takeaway:
● To identify patterns, finite state machines are used.
● FA has two states: state approve or state deny.
● In DFA, the character of the input goes to only one state.
● Simple expressions called Regular Expressions can readily define the language adopted by finite automata. This is the most powerful way of expressing any language.
● Regular languages are referred to as the languages recognized by certain regular expressions.
● A regular expression may also be defined as a pattern sequence that defines a series.
● For matching character combinations in strings, regular expressions are used. This pattern is used by the string search algorithm to locate operations on a string.
A Regular Expression can be recursively defined as follows −
● ε is a Regular Expression indicates the language containing an empty
String. (L (ε) = {ε})
● φ is a Regular Expression denoting an empty language. (L (φ) = { })
● x is a Regular Expression where L = {x}
● If X is a Regular Expression denoting the language L(X) and Y is a Regular
● Expression denoting the language L(Y), then
● X + Y is a Regular Expression corresponding to the language L(X) ∪ L(Y) where L(X+Y) = L(X) ∪ L(Y).
● X . Y is a Regular Expression corresponding to the language L(X) . L(Y) where L(X.Y) = L(X) . L(Y)
● R* is a Regular Expression corresponding to the language L(R*) where L(R*) = (L(R))*
● If we apply any of the rules several times from 1 to 5, they are Regular Expressions.
Unix Operator Extensions
Regular expressions are used frequently in Unix:
● In the command line
● Within text editors
● In the context of pattern matching programs such as grep and egrep
Additional operators are recognized by unix. These operators are used for convenience only.
● character classes: ‘[‘ <list of chars> ‘]’
● start of a line: ‘^’
● end of a line: ‘$’
● wildcard matching any character except newline: ‘.’
● optional instance: R? = epsilon | R
● one or more instances: R+ == RR*
Key takeaway:
● Regular languages are referred to as the languages recognized by certain regular expressions.
● A regular expression may also be defined as a pattern sequence that defines a series.
Regular expressions and finite automata have equivalent expressive power:
● For every regular expression R, there is a corresponding FA that accepts the set of strings generated by R.
● For every FA , A there is a corresponding regular expression that generates the set of strings accepted by A.
The proof is in two parts:
1. An algorithm that, given a regular expression R, produces an FA A such that
L(A) == L(R).
2. An algorithm that, given an FA A, produces a regular expression R such that
L(R) == L(A).
Our construction of FA from regular expressions will allow “ epsilon transitions ” (a transition from one state to another with epsilon as the label). Such a transition is always possible, since epsilon (or the empty string) can be said to exist between any two input symbols. We can show that such epsilon transitions are a notational convenience; for every FA with epsilon transitions there is a corresponding FA without them.
Constructing an FA from an RE
We begin by showing how to construct an FA for the operands in a regular Expression.
● If the operand is a character c, then our FA has two states, s0 (the start state) and sF (the final, accepting state), and a transition from s0 to sF with label c.
● If the operand is epsilon, then our FA has two states, s0 (the start state) and sF (the final, accepting state), and an epsilon transition from s0 to sF.
● If the operand is null, then our FA has two states, s0 (the start state) and sF (the final, accepting state), and no transitions.
Given FA for R1 and R2, we now show how to build an FA for R1R2, R1|R2, and R1*. Let A (with start state a0 and final state aF) be the machine accepting L(R1) and B (with start state b0 and final state bF) be the machine accepting L(R2).
● The machine C accepting L(R1R2) includes A and B, with start state a0, final state bF, and an epsilon transition from aF to b0.
● The machine C accepting L(R1|R2) includes A and B, with a new start state c0, a new final state cF, and epsilon transitions from c0 to a0 and b0, and from aF and bF to cF.
● The machine C accepting L(R1*) includes A, with a new start state c0, a new final state cF, and epsilon transitions from c0 to a0 and cF, and from aF to a0, and from aF to cF.
Eliminating Epsilon Transitions
If epsilon transitions can be eliminated from an FA, then construction of an FA from a regular expression can be completed.
Epsilon transitions offers a choice: It allows us to stay in a state or move to a new state, regardless of the input symbol.
If starting in state s1, state s2 can be reached via a series of epsilon transitions followed by a transition on input symbol x, replacement of the epsilon transitions with a single transition from s1 to s2 on symbol x.
Algorithm for Eliminating Epsilon Transitions
A finite automaton F2 can be build with no epsilon transitions from a finite automaton F1 as follows:
1. The states of F2 are all the states of F1 that have an entering transition labeled by some symbol other than epsilon, plus the start state of F1, which is also the start state of F2.
2. For each state in F1, determine which other states are reachable via epsilon transitions only. If a state of F1 can reach a final state in F1 via epsilon transitions, then the corresponding state is a final state in F2.
For each pair of states i and j in F2, there is a transition from state i to state j on input x if there exists a state k that is reachable from state i via epsilon transitions in F1, and there is a transition in F1 from state k to state j on input x.
Key takeaway:
● For every regular expression, there is a corresponding FA that accepts the
Set of strings generated by RE.
● The computer can switch to any combination of states in the NDFA.
● Epsilon closure for a given state X is a set of states that can only be reached with (null) or ε moves from states X, including state X itself.
● When the computer is given a single input to a single state, it goes to a single state in DFA.
Lex is a lexical analyzer generating programme. It is used to produce the YACC parser. A software that transforms an input stream into a sequence of tokens is the lexical analyzer. It reads the input stream and, by implementing the lexical analyzer in the C programme, produces the source code as output.
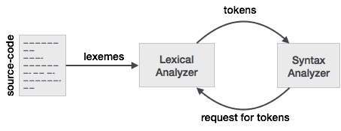
Fig 3: lexical analyzer generator
If a token is considered invalid by the lexical analyzer, it produces an error. The lexical analyzer works with the syntax analyzer in close collaboration. It reads character streams from the source code, checks for legal tokens, and, when necessary, passes the information to the syntax analyzer.
Tokens
It is said that lexemes are a character sequence (alphanumeric) in a token. For each lexeme to be identified as a valid token, there are some predefined rules. These rules, by means of a pattern, are described by grammar rules. A pattern describes what a token can be, and by means of regular expressions, these patterns are described.
Keywords, constants, identifiers, sequences, numbers, operators and punctuation symbols can be used as tokens in the programming language.
Example: the variable declaration line in the C language
Int value = 100;
Contains the tokens:
Int (keyword), value (identifiers) = (operator) , 100 (constant) and ; (symbol)
Functions of lex:
● Firstly, in the language of Lex, the lexical analyzer produces a lex.1 programme. The Lex compiler then runs the lex.1 programme and generates the lex.yy.c C programme.
● Finally, the programmer C runs the programme lex.yy.c and generates the object programme a.out.
● A.out is a lexical analyzer which converts an input stream into a token sequence.

Fig 4: lex compiler
Lex file format:
By percent percent delimiters, a Lex programme is divided into three parts. The structured sources for Lex are as follows:
{ definitions }
%%
{ rules }
%%
{ user subroutines }
Definitions include constant, variable and standard meaning declarations.
The rules describe the form statement p1 {action1} p2 {action2}....pn {action} p2 form p1....pn {action}
Where pi describes the regular expression and action1 describes the behavior that should be taken by the lexical analyzer when a lexeme matches the pattern pi.
Auxiliary procedures required by the acts are user subroutines. It is possible to load the subroutine with the lexical analyser and compile it separately.
Flex
A tool for scanner generation is FLEX (Fast LEXical analyzer generator). You just need to define the vocabulary of a certain language, write a pattern specification using regular expressions (e.g. DIGIT [0-9]) instead of writing a scanner from scratch, and FLEX will create a scanner for you.
In general, FLEX is used in the manner represented here:
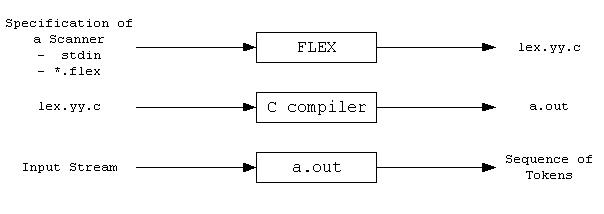
Fig 5: Flex
First, FLEX reads a scanner specification either from an input file *.lex or from a standard input and generates a lex.yy.c source C file as the output. Then, to create an executable a.out, lex.yy.c is compiled and connected to the '-lfl' library. Finally, a.out analyses and transforms the input stream into a token sequence.
● *.Lex comes in the form of regular expressions and C code pairs.
● A yylex() routine specifies lex.yy.c, which uses the specification to identify tokens.
● Currently, A.out is a scanner!
Key takeaway:
● It is said that lexemes are a character sequence (alphanumeric) in a token.
● For each lexeme to be identified as a valid token, there are some predefined rules.
● A Lexical analyzer is used to produce the YACC parser.
● A tool for scanner generation is FLEX (Fast LEXical analyzer generator
References:
- Compilers Principles Techniques And Tools by Alfred V.Aho. Ravi Sethi Jeffery D.Ullman. Pearson Education.
- Modern Compiler Design by Dick Grune . E. Bal. Ceriel J. H. Jacobs. And Koen G. Langendoen Viley Dreamtech.
- Http://alumni.cs.ucr.edu/