Unit - 2

Syntax Analysis (Parser)

2.1 Context-free languages and grammars

Context-free grammar (CFG) is a collection of rules (or productions) for recursive rewriting used to produce string patterns.

It consists of:

●      a set of terminal symbols,

●      a set of non-terminal symbols,

●      a set of productions,

●      a start symbol.

Context-free grammar G can be defined as:

G = (V, T, P, S)

Where 

G - grammar, used for generate string,

V - final set of non terminal symbol, which are denoted by capital letters,

T - final set of terminal symbol, which are denoted be small letters,

P - set of production rules, it is used for replacing non terminal symbol of a string in both side (left or right)

S - start symbol, which is used for derive the string

A CFG for Arithmetic Expressions -

An example grammar that generates strings representing arithmetic expressions with the four operators +, -, *, /, and numbers as operands is:

1. <expression> --> number

2. <expression> --> (<expression>)

3.<expression>  --> <expression> +<expression>

4. <expression> --> <expression> - <expression>

5. <expression> --> <expression> * <expression>

6. <expression> --> <expression> / <expression>

The only non terminal symbol in this grammar is <expression>, which is also the start symbol. The terminal symbols are {+,-,*,/ , (,),number}

●      The first rule states that an <expression> can be rewritten as a number.

●      The second rule says that an <expression> enclosed in parentheses is also an <expression>

●      The remaining rules say that the sum, difference, product, or division of two <expression> is also an expression.

Context free language (CFL)

A context-free language (CFL) is a language developed by context-free grammar (CFG) in formal language theory. In programming languages, context-free languages have many applications, particularly most arithmetic expressions are created by context-free grammars.

●      Through comparing different grammars that characterise the language, intrinsic properties of the language can be separated from extrinsic properties of a particular grammar.

●      In the parsing stage, CFLs are used by the compiler as they describe the syntax of a programming language and are used by several editors.

A grammatical description of a language has four essential components -

1. There is a set of symbols that form the strings of the language being defined. They are called terminal symbols, represented by V t .
2. There is a finite set of variables, called non-terminals. These are represented by V n .
3. One of the variables represents the language being defined; it is called the start symbol. It is represented by S.
4. There are a finite set of rules called productions that represent the recursive definition of a language. Each production consists of:

●      A variable that is being defined by the production. This variable is also called the production head.

●      The production symbol ->

●      A string of zero terminals and variables, or more.

Key takeaway:

●      CFG is a collection of rules (or productions) for recursive rewriting used to produce string patterns.

●      CFL is a language developed by context-free grammar (CFG) in formal language theory.

2.2 Push-down automata

Pushdown automata is a way for a CFG to be implemented in the same way that we build a standard grammar DFA. A DFA can remember a finite amount of information, but an infinite quantity of information can be recalled by a PDA.

Pushdown automatics are essentially "external stack memory"-enhanced NFA. The stack addition is used to provide Pushdown Automata with a last-in-first-out memory management feature.

An unbounded amount of information can be stored on the stack by pushdown automata. On the stack, it can access a small amount of knowledge. A PDA will push an element from the top of the stack onto the top of the stack and pop an element off. The top elements have to be popped off and are lost in order to read an element into the stack.

A PDA is better than an FA. Any language acceptable to the FA may also be acceptable to the PDA. The PDA even recognises a language class that cannot even be recognised by the FA. Thus, the PDA is much stronger than the FA.

Fig 1: Push down automata

It is possible to formally define a PDA as a 7-tuple (Q, ∑, S, δ, q0, I, F) −

●       Q - finite number of states

●       ∑ - input alphabet

●       S - stack symbols

●       δ - transition function: Q × (∑ ∪ {ε}) × S × Q × S*

●       q0 - initial state (q0 ∈ Q)

●       I - initial stack top symbol (I ∈ S)

●       F - set of accepting states (F ∈ Q)

Key takeaway:

●      A pushdown automaton is a way for a context-free grammar to be implemented in the same way that we build a standard grammar DFA.

●      A DFA can remember a finite amount of information, but an infinite quantity of information can be recalled by a PDA.

2.3 LL(1) grammars and top-down parsing

It is also known with or without a backtracking parser or dynamic parser, LL(1) parser or predictive parser. It uses the parsing table instead of backtracking to create the parsing tree.

Predictive parser is a recursive descent parser, which has the capability to predict which production is to be used to replace the input string. The predictive parser does not suffer from backtracking.

To accomplish its tasks, the predictive parser uses a look-ahead pointer, which points to the next input symbols. To make the parser back-tracking free, the predictive parser puts some constraints on the grammar and accepts only a class of grammar known as LL(k) grammar.

Predictive parsing uses a stack and a parsing table to parse the input and generate a parse tree. Both the stack and the input contains an end symbol $ to denote that the stack is empty and the input is consumed. To take some decision on the input and stack element combination, the parser refers to the parsing table.

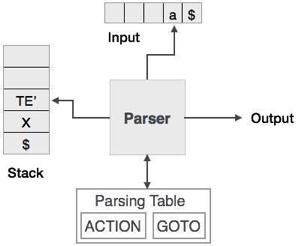
Fig 2: predictive parser

In recursive descent parsing, for a single instance of input, the parser can have more than one output to choose from, while in predictive parser, each stage has at most one production to choose from. There may be instances where the input string does not fit the production, making the parsing procedure fail.

Top - down Parsing

It is also known as Brute force parser or the with backtracking parser. Basically, by using brute force and backtracking, it produces the parse tree.

A top-down parsing technique that builds the parse tree from the top and reads the input from left to right is recursive descent. For any terminal and non-terminal entity, it uses procedures.

The input is recursively parsed by this parsing technique to make a parse tree, which may or may not require back-tracking. But the related grammar (if not left-faced) does not prevent back-tracking. Predictive is considered a type of recursive-descent parsing that does not require any back-tracking.

As it uses context-free grammar that is recursive in nature, this parsing technique is called recursive.

Key takeaway:

●      A top-down parsing technique that builds the parse tree from the top and reads the input from left to right is recursive descent.

●      The input is recursively parsed by this parsing technique to make a parse tree, which may or may not require back-tracking.

●      Predictive parser is a recursive descent parser, which has the capability to predict which production is to be used to replace the input string.

2.4 Operator grammars

The grammar of operator precedence is a kind of shift reduction system of parsing. It is applied to a small grammar class of operators.

A grammar, if it has two properties, is said to be operator precedence grammar:

●      There's no R.H.S. Of any production.

●      There are no two adjoining non-terminals.

Operator precedence can only be defined between the terminals of the grammar. A non-terminal is overlooked.

The three operator precedence relations exist:

●      a ⋗  b suggests that the precedence of terminal "a" is greater than terminal "b"

●      a ⋖ b means the lower precedence of terminal "a" than terminal "b"

●      a ≐  b indicates that all terminals "a" and "b" have the same precedence.

Precedence table:

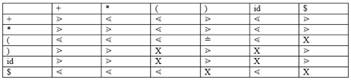
Parsing Action

●      Add the $ symbol at both ends of the specified input string.

●      Now search the right-left input string until the ⁇ is encountered.

●      Scan to the left over all of the equal precedence until much of the first left is met.

●      A handle is anything between most of the left and most of the right.

●      $ on $ means the parsing succeeds.

Example - Grammar:

1. E → E+T/T 
2. T → T*F/F 
3. F → id 

Given string:

1. w = id + id * id 

For it, let us take a parse tree as follows:

We can design the following operator precedence table on the basis of the tree above:

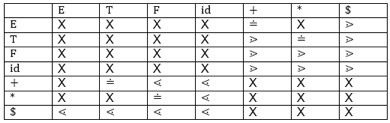
Let us now process the string with the assistance of the precedence table above:

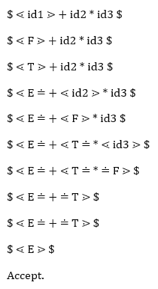
Key takeaway:

2.5 LR(O)

An LR (0) object is an output G with a dot on the right side of the production at a certain location.

LR(0) items are useful for showing how much of the input has been scanned in the parsing phase up to a given stage.  We position the reduction node in the entire row in the LR (0).

We increase the grammar and get a fresh output of this one; take its closure. That is the collection's first element; call it Z (we will actually call it I0).Try GOTO from Z, i.e. consider GOTO(Z,X) for each grammar symbol; each of these (almost) is another element of the set.

From each of these new elements of the set, try GOTOing now, etc. Start with Jane Smith, add F to all her friends, then add F to everyone's friends in F, named FF, then add FF to everyone's friends, etc.

The (almost) is because GOTO(Z,X) may be empty, so we formally create the LR(0) items canonical set, C, as follows :

1. Initialize C = CLOSURE({S' → S})
2. If I is in C, X is a grammar symbol, and GOTO(I,X)≠φ then add it to C and repeat.

In the DFA I created earlier, this GOTO gives exactly the arcs. Formal therapy does not include the NFA, but starts from the beginning of the DFA.

Example -

    E' → E

    E → E + T | T

    T → T * F | F

    F → ( E ) | id

It's bigger than the toy that I made before. The NFA will have 2+4+2+4+2+4+2=20 states (a development on the RHS with k symbols gives k+1 N-states as there are k+1 places to position the dot). This brings 12 D-states into being. The creation in the book, which we are following now, however, explicitly constructs the DFA.

Begin to build the diagram on the platform:

Start with {E ' → ·E}, close the lock, and then proceed to apply GOTO.

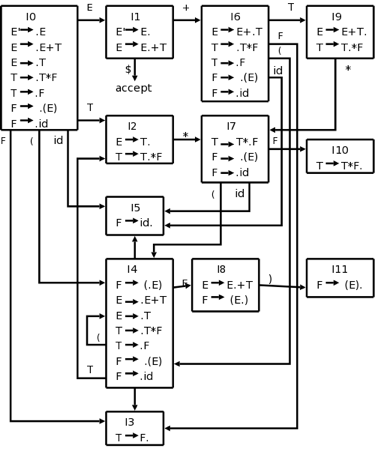
Fig 3: DFA diagram

Key takeaway:

●      LR(0) items are useful for showing how much of the input has been scanned in the parsing phase up to a given stage.

2.6 SLR(1)

SLR (1) refers to fast parsing of LR. It's the same as parsing for LR(0). The only difference is in the parsing table. We use a canonical LR (0) item array to create the SLR (1) parsing table.

We just position the reduction step in the follow-up of the left hand side in the SLR (1) parsing.

Different steps related to SLR (1) Parsing:

●      Write a context free grammar for the specified input string

●      Verify the grammar's uncertainty

●      Add Increase output in the grammar specified

●      Build a canonical set of things from LR (0)

●      Drawing a diagram of data flow (DFA)

●      Build an SLR (1) table for parsing

SLR(1) Table Construction :

Start at rule zero for the rules in an augmented grammar, G ', and follow the steps below:

Steps of State Formation (big picture algorithm)

1. Apply the Start and Start operations

2. Attain the State:

1. Using one reading operation in the current state on . Item C (non-terminal or terminal)  form more states.
2. Apply the whole procedure to the new nations.
3. Repeat steps a and b until it is possible to form no more new states.

Example:

Consider the augmented grammar G'

S’ ‐‐>  S$

S  ‐‐>  aSbS

S  ‐‐>  a

The set of Item Sets LR(0), states:

I0     [S’ -> .S$]  (Operation to start; read on S goes to I11 (state 1)  )

        [S -> .aSbS] (Full S rule operation; the reading on 'a' goes to I2 (state 2) )

        [S -> .a] (For all rules 'S', continue to complete; read on 'a', to state 2 )

I1      [S’ -> S.$] (From the first line, read on 'S'; Note: never read on '$'

Nothing to read about; nothing to end )

I2      [S -> a.SbS] (Reading from state I0 on 'a'; reading on'S 'goes to I3 (state 3) )

[S -> a.]  (Continue reading on 'a' from state I0 (see stage 2 of formation of state)   with nothing to read on; nothing to complete )

[S -> .aSbS] (Complete the state in the first item read on 'a' cycles back to state 2  because of '.S' )

[S -> .a] (All grammar rules for 'S' ditto read on 'a' cycles remain full back to state 2 )

I3       [S -> aS.bS] (The dot is before a non-terminal from the reading on'S 'from state I2,                    no full operation read on' b 'goes to I4 (state 4) )

I4 [S -> aSb.S] (From reading from state I3 on 'b'; reading from'S 'goes to I5 (state 5) )

    [S -> .aSbS] (Due to the '.S' in the first object, complete the state;

                        Note: always dot in front for complete points

                       Return to State 2 read on 'a' cycles )

     [S -> .a] ( Continue complete; ditto read back to state 2 on 'a' cycles )

I5  [S -> aSbS.] (From state 5 to read on 'S'; nothing to read on )

Construct the parse table:

You need the FIRST and FOLLOW sets for each non-terminal in your grammar to construct the parsing table.

You will need the completed collection of products for the state from above.

Now, for your parse table, draw the n x m table and mark it appropriately. The n is equal to the number of states from part 1 that you have. By counting all non-terminals and all terminals in the grammar, you decide the M. Provide a row or column for each element of n and m.

Label each row n, starting at zero, with a state number. Mark each column m, beginning from left to right, with one terminal per column. Labeling the remaining columns after labelling with all the terminals

With those non-terminals.

The ACTION side is the group of columns on the left (terminals). The group of columns is the GOTO side on the right (non-terminals)

You obey these four rules to fill out the table,

Construction rules

α, β = any string of terminals and/or non‐terminals

X, S’, S = non‐terminals

(When dot is in middle)

1. If [A ‐‐> α.aβ] ε Ii and read on ‘a’ produces Ij then ACTION [i , a] = SHIFT j.

2. If [A ‐‐> α.Xβ] ε Ii and read on ‘X’ produces Ij then GOTO [i , X] = j.

(When dot is at end)

3. If [A ‐‐> α.] ε Ii then ACTION [i , a] = REDUCE on A ‐> α for all a ε FOLLOW(A).

4. If [S’ ‐‐> S.] ε Ii then ACTION [i , $] = ACCEPT.

For example, the parsing table:

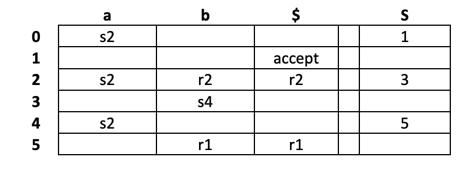
Key takeaway:

●      SLR (1) refers to fast parsing of LR.

●      It's the same as parsing for LR(0).

2.7 LR(1)

Different steps involved in LR (1) Parsing:

●      Write context-free grammar for the specified input string.

●      Verify the grammar's uncertainty.

●      Add the Augmentation output to the specified grammar.

●      Creating a canonical set of objects from LR (0).

●      Drawing a diagram of data flow (DFA).

●      Build a table for LR (1) parsing.

Augment Grammar:

If we add one more output to the given grammar G, Augmented Grammar G will be generated. It allows the parser to define when the parsing should be stopped and to announce the acceptance of the input.

Example

Given grammar

S → AA 

A → aA | b 

The Augment grammar G is represented by

1. S→ S 
2. S → AA 
3. A → aA | b

Key takeaway:

●      The current symbol in the input string is moved into the stack for the shift operation.

●      The shifted symbol will be viewed as a single parse tree node.

●      LR(1) parser Verify the grammar's uncertainty.

●      In the LR parser, “ L” means left to right scanning of any input .

2.8 LALR(1) grammars and bottom-up parsing

The lookahead LR is alluded to by LALR. We use the canonical set of LR (1) objects to create the LALR (1) parsing table.

In the LALR (1) analysis, the LR (1) products that have the same outputs but look ahead differently are combined to form a single set of items

The parsing of LALR(1) is the same as the parsing of CLR(1), the only distinction in the parsing table.

LALR (1) Parsing:

LALR refers to the lookahead LR. To construct the LALR (1) parsing table, we use the canonical collection of LR (1) items.

In the LALR (1) parsing, the LR (1) items which have same productions but different look ahead are combined to form a single set of items

LALR (1) parsing is the same as the CLR (1) parsing, only difference in the parsing table.

Example

LALR ( 1 ) Grammar

1. S → AA 
2. A  → aA 
3. A → b 

Add Augment Production, insert the '•' symbol for each production in G at the first place and add the look ahead as well.

S → •S, $ 

S  → •AA, $ 

A  → •aA, a/b  

A  → •b, a/b 

I0 State:

Add the output of Augment to the I0 State and measure Closure L

I0 = Closure (S → •S)

Add all productions beginning with S to I0 State, since the non-terminal is followed by '•'. The I0 Condition, then, becomes

I0 = S → •S, $

        S → •AA, $

In changed I0 State, add all productions beginning with A since "•" is followed by the non-terminal. So, it will become the I0 State.

I0= S → •S, $

   S → •AA, $

   A → •aA, a/b

   A → •b, a/b

I1= Go to (I0, S) = closure (S → S•, $) = S → S•, $

I2= Go to (I0, A) = closure ( S → A•A, $ )

In the I2 State, add all productions beginning with A since "•" is followed by the non-terminal.

Bottom - up Parsing

Bottom up parsing is also known as parsing for shift-reduce.

Bottom-up parsing is used to build an input string parsing tree.

The parsing begins with the input symbol in the bottom up parsing and builds the parse tree up to the start symbol by tracing the rightmost string derivations in reverse.

Parsing from the bottom up is known as multiple parsing. That are like the following:

1. Shift-Reduce Parsing
2. Operator Precedence Parsing
3. Table Driven LR Parsing

1. LR( 1 )
2. SLR( 1 )
3. CLR ( 1 )
4. LALR( 1 )

Shift - reduce parsing:

●      Shift reduction parsing is a mechanism by which a string is reduced to the beginning symbol of a grammar.

●      Using a stack to hold the grammar and an input tape to hold the string, Shift reduce parsing.

●      The two acts are done by Shift Decrease Parsing: move and decrease. This is why it is considered that shift reduce parsing.

●      The current symbol in the input string is moved into the stack for the shift operation.

●      The symbols will be substituted by the non-terminals at each reduction. The mark is the right side of manufacturing and the left side of output is non-terminal.

Key takeaway:

●      Bottom-up parsing is used to build an input string parsing tree.

●      Parsing from the bottom up is known as multiple parsing.

●      Shift reduction parsing is a mechanism by which a string is reduced to the beginning symbol of a grammar.

2.9 Ambiguity and LR parsing

You may use the LR parser to parse ambiguous grammar. In the parsing table of ambiguous grammars, the LR parser resolves the conflicts (shift/reduce or decrease/reduce) based on certain grammar rules (precedence and/or associativity of operators).

Example:

Let's take the unclear grammar below:

E -> E+E

E -> E*E

E -> id

The precedence and associativity of the grammar operators (+ and *) can be considered to be as follows:

●      “+” and “*” both are left associative,

●      Precedence of “*” is higher than the precedence of “+”.

If we use LALR(1) parser, the LR(1) item DFA will be:

Fig 4: LR (1) item DFA

We can see from the LR(1) DFA item that there are shift/reduce conflicts in the I5 and I6 states.

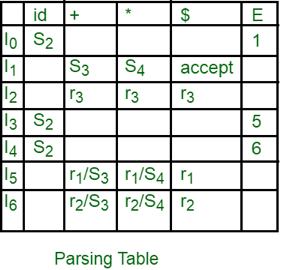
Fig: parsing table

"In I5 and I6, moves on "+ and "*" are both moved and decreased. To settle this dispute, we will use the precedence and associativity of the operators to decide which phase to preserve and which to discard from the table.

LR Parsing

LR parsing is divided into four parts: parsing for LR (0), parsing for SLR, parsing for CLR and parsing for LALR.

LR algorithm:

The stack, input, output and parsing table are required by the LR algorithm. The input, output and stack are the same in all modes of LR parsing, but the parsing table is different.

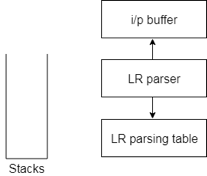
Fig 5: diagram of LR parser

Key takeaway:

●      In the parsing table of ambiguous grammars, the LR parser resolves the conflicts based on certain grammar rules .

●      In the LR parser, “ L” means left to right scanning of any input .

●      The stack, input, output and parsing table are required by the LR algorithm.

2.10 LALR(1) parser generator (yacc, bison)

YACC is an automatic tool which generates the programme for the parser.

YACC stands for Compiler Compiler Yet Another. The software is available under UNIX OS OS

LR parser construction requires a lot of work for the input string to be parsed.

Therefore, in order to achieve productivity in parsing and data, the procedure must provide automation.

Basically, YACC is an LALR parser generator that reports conflicts or uncertainties in the form of error messages (if at all present).

As we addressed YACC in the first unit of this tutorial, to make it more understandable, you can go through the concepts again.

●      YACC

As shown in the picture, the standard YACC translator can be represented as

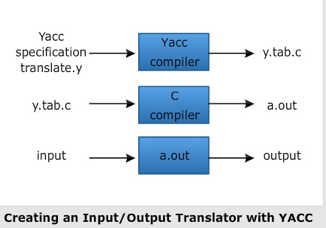
Fig 6: YACC automatic parser generator

Biscon

The bison is a generator parser. What flex is to scanners is to parsers. You provide a grammar specification input, and an LALR(1) parser is created to recognise sentences in that grammar. A great example of a CS joke is the word. Bison is an improved version of "yet another compiler compiler" of the older yacc tool, and it is possibly the most popular LALR tool out there.

Bison is intended for use with the C language and produces a C-written parser. In conjunction with a flex-generated scanner, the parser is designed for use and relies on standard shared features (token types, yylval, etc.) and calls the function yylex as a scanner coroutine.

A grammar specification file is given, which is usually called using an extension of .y. On the .y file, you invoke bison and it generates the y.tab.h and y.tab.c files containing around a thousand lines of intense C code that implements your grammar's successful LALR(1) parser, including the code for the actions you defined.

File format

%{

Declarations

%}

Definitions

%%

Productions

%%

User subroutines

Key takeaway:

●      YACC is an automatic tool which generates the programme for the parser.

●      YACC is an LALR parser generator that reports conflicts or uncertainties in the form of error messages (if at all present).

●      Bison is intended for use with the C language and produces a C-written parser.

●      The bison is a generator parser.

References:

1. Compilers Principles Techniques And Tools by Alfred V. Aho. Ravi Sethi Jeffery D .Ullman. Pearson Education.
2. Compiler Design by Santanu Chattopadhyay. PHI
3. Https://web.stanford.edu