Unit - 1
Introduction
At a high-level, machine learning is simply the study of teaching a computer programme or algorithm how to gradually improve upon a set task that it is given. On the research-side of things, machine learning can be seen through the prism of theoretical and mathematical simulation of how this method works. However, more technically it is the study of how to construct applications that exhibit this iterative progress.
Machine Learning is an Application of Artificial Intelligence (AI) that gives machines the opportunity to learn from their experiences and develop themselves without doing any coding.
Machine Learning is a branch of Artificial Intelligence. Machine Learning is the study of making machines more human-like in their actions and decisions by allowing them the ability to learn and create their own programmes. This is achieved with minimal human interference, i.e., no explicit programming. The learning process is automated and enhanced based on the experiences of the machines in the process.
There are Seven Steps of Machine Learning
- Gathering Data
- Preparing that data
- Choosing a model
- Training
- Evaluation
- Hyperparameter Tuning
- Prediction
Key takeaway:
● Machine Learning is an Application of Artificial Intelligence (AI) that gives machines the opportunity to learn from their experiences and develop themselves without doing any coding.
● On the research-side of things, machine learning can be seen through the prism of theoretical and mathematical simulation of how this method works.
Linear Algebra is a branch of mathematics that lets you concisely define coordinates and interactions of planes in higher dimensions and perform operations on them.
Think of it as an extension of algebra (dealing with unknowns) over an infinite number of dimensions. Linear Algebra is about operating on linear systems of equations (linear regression is an example: y = Ax). Rather than dealing with scalars, we start working with matrices and vectors (vectors are actually just a special form of matrix) (vectors are really just a special type of matrix).
Linear algebra finds widespread use because it typically parallelizes extremely well. Further to that most linear algebra operations can be implemented without messaging passing which makes them amenable to MapReduce implementations.
If I was to persuade you to learn a minimum of linear algebra to boost your capabilities in machine learning, it would be the following 3 topics:
Notation: Learning the notation can let you read algorithm explanations in journals, books and websites to get an understanding of what is going on. And if you use for-loops rather than matrix operations, at least you will be able to piece things together.
Operations: Working at the next stage of abstraction in vectors and matrices will make it simpler. This can refer to explanations, to code and even to thought. Learn how to do or apply basic operations like combining, multiplying, inverting, transposing, etc. matrices and vectors.
Matrix Factorization: If there was one deeper area I would suggest digging into over any other it would be matrix factorization, specifically matrix deposition methods like SVD and QR. The numerical precision of computers is minimal and working with decomposed matrices helps you to sidestep a lot of the overflow/underflow madness that can result.
Linear algebra plays a requisite role in machine learning due to vectors’ availability and many rules to manage vectors. We often tackle classifiers or regressor problems in machine learning, and then error minimization techniques are implemented by computing from real value to expected value. Consequently, we use linear algebra to manage the before-mentioned sets of computations. Linear algebra manages vast numbers of data, or in other words, “linear algebra is the basic mathematics of data.”
These are some of the fields in linear algebra that we use in machine learning (ML) and deep learning:
● Vector and Matrix.
● System of Linear Equations.
● Vector Space.
● Basis
Also, these are the fields of machine learning (ML) and deep learning, where we apply linear algebra’s methods:
- Derivation of Regression Line.
- Linear Equation to predict the target value.
- Support Vector Machine Classification (SVM).
- Dimensionality Reduction.
- Mean Square Error or Loss function.
- Regularization.
- Covariance Matrix.
- Convolution.
Key takeaway:
● Linear Algebra is a branch of mathematics that lets you concisely define coordinates and interactions of planes in higher dimensions and perform operations on them.
● Linear algebra plays a requisite role in machine learning due to vectors’ availability and many rules to manage vectors.
Statistical learning theory is a basis for machine learning, drawing from the fields of statistics and functional analysis.
Statistical learning theory deals with the issue of seeking a predictive function based on data.
The objective of learning is prediction. Learning falls into several categories, including:
● Supervised learning,
● Unsupervised learning,
● Semi-supervised learning
● Transfer Learning
● Online learning, and
● Reinforcement learning.
From the analysis of statistical learning theory, supervised learning is better described.
In supervised learning, an algorithm is given samples that are labelled in a useful way. For example, the samples may be descriptions of apples, and the marks may be whether or not the apples are edible.
Supervised learning requires learning from a training collection of data. Every point in the training is an input-output pair, where the input maps to an input. The learning problem consists of inferring the function that maps between the input and the output in a predictive manner, so that the a learned function can be used to predict output from future input.
The algorithm takes these previously labelled samples and uses them to induce a classifier. This classifier is a function that assigns labels to samples including the samples that have never been previously seen by the algorithm.
The aim of the supervised learning algorithm is to optimize some measure of results such as minimizing the number of mistakes made on new samples.
Machine Learning | Statics |
Network, graph | Model |
Weights | Parameter |
Learning | Fitting |
Generalization | Test set performance |
Supervised Learning | Regression / classification |
Unsupervised Learning | Density estimation , clustering |
Statistical modelling typically works with a number of assumptions.
For instance a linear regression assumes:
1. Linear relation between independent and dependent variable
2. Homoscedasticity
3. Mean of error at zero for any dependent value
4. Freedom of findings
5. Error should be normally distributed for each value of dependent variable
Key takeaway:
● Statistical learning theory is a basis for machine learning, drawing
From the fields of statistics and functional analysis.
● Statistical learning theory deals with the issue of seeking a predictive
Function based on data.
There are several ways to frame this definition, but largely there are three main known categories: supervised learning, unsupervised learning, and reinforcement learning.
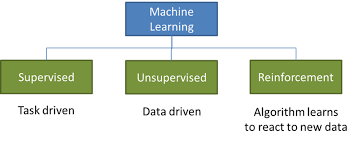
Fig 1: types of Learning
In a world filled by artificial intelligence, machine learning, and over-zealous talk about both, it is interesting to learn to understand and define the types of machine learning we may encounter. For the average computer user, this may take the form of knowing the forms of machine learning and how they can exhibit themselves in applications we use.
And for the practitioners designing these applications, it’s important to know the styles of machine learning so that for any given task you can face, you can craft the proper learning environment and understand why what you did succeeded.
- Supervised Learning
Supervised learning is the most common model for machine learning. It is the easiest to grasp and the quickest to execute. It is quite close to training a child through the use of flash cards.
Supervised learning is also defined as task-oriented because of this. It is highly focused on a single task, feeding more and more examples to the algorithm before it can reliably perform on that task.
There are two major types of supervised learning problems: classification that involves predicting a class mark and regression that involves predicting a numerical value.
● Classification: Supervised learning problem that involves predicting a class mark.
● Regression: Supervised learning problem that requires predicting a numerical mark.
Both classification and regression problems can have one or more input variables and input variables may be any data form, such as numerical or categorical.
2. Unsupervised Learning
Unsupervised learning is very much the opposite of supervised learning. It features no marks. Instead, our algorithm will be fed a lot of data and provided the tools to understand the properties of the data. From there, it can learn to group, cluster, and/or arrange the data in a way so that a person (or other intelligent algorithm) can come in and make sense of the newly arranged data.
There are several forms of unsupervised learning, but there are two key problems that are mostly faced by a practitioner: they are clustering that involves identifying groups in the data and density estimation that involves summarising the distribution of data.
● Clustering: Unsupervised learning problem that involves finding groups in data.
● Density Estimation: Unsupervised learning problem that involves summarizing the distribution of data.
3. Reinforcement Learning
Reinforcement learning is fairly different when compared to supervised and unsupervised learning. Where we can clearly see the relationship between supervised and unsupervised (the existence or absence of labels), the relationship to reinforcement learning is a little murkier. Some people attempt to tie reinforcement learning closer to the two by defining it as a form of learning that relies on a time-dependent sequence of labels, however, my opinion is that that actually makes things more complicated.
For any reinforcement learning challenge, we need an agent and an environment as well as a way to link the two via a feedback loop. To link the agent to the world, we give it a collection of actions that it can take that affect the environment. To link the environment to the agent, we make it continually issue two signals to the agent: an updated state and a reward (our reinforcement signal for behavior) (our reinforcement signal for behavior).
Key takeaway:
● Supervised learning is the most common model for machine learning. It is the easiest to grasp and the quickest to execute.
● Unsupervised learning is very much the opposite of supervised learning. It features no marks. Instead, our algorithm will be fed a lot of data and provided the tools to understand the properties of the data.
● Reinforcement learning is fairly different when compared to supervised and unsupervised learning.
In most supervised machine learning algorithms, our main aim is to figure out a potential hypothesis from the hypothesis space that could potentially map out the inputs to the correct outputs.
The following figure shows the common method to find out the possible hypothesis from the Hypothesis space:
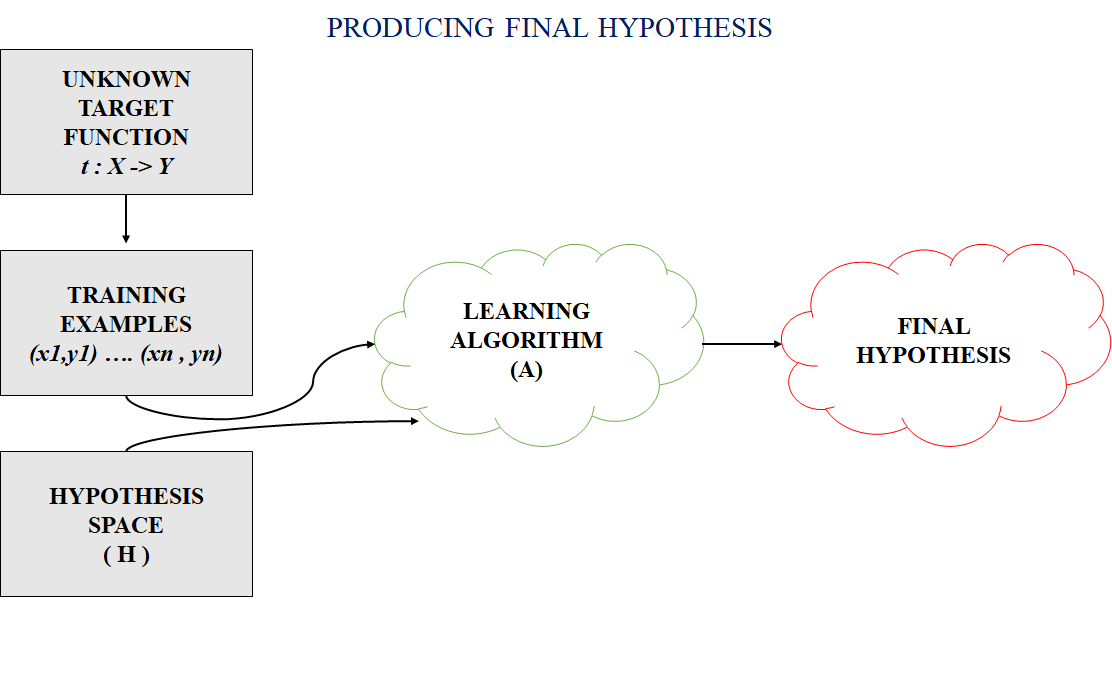
Fig 2: hypothesis space
Hypothesis Space (H):
Hypothesis space is the set of all the possible legal hypothesis. This is the set from which the machine learning algorithm will decide the best possible (only one) which would best represent the target function or the outputs.
Hypothesis (h):
A hypothesis is a function that best describes the goal in supervised machine learning. The hypothesis that an algorithm will come up depends upon the data and also depends upon the constraints and prejudice that we have put on the data. To better understand the Hypothesis Space and Hypothesis consider the following coordinate that shows the distribution of some data:
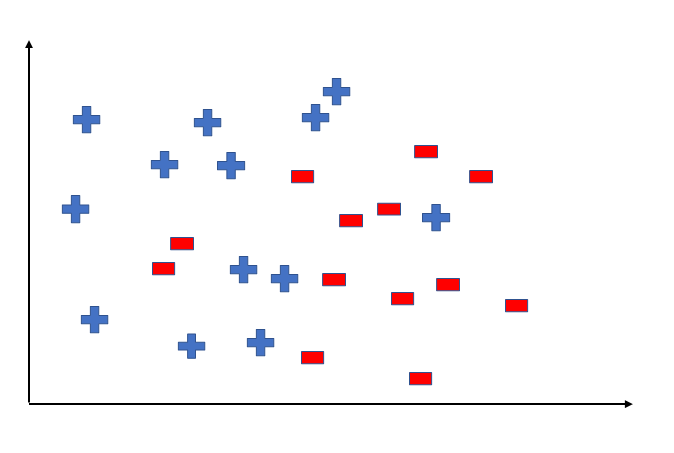
Fig 3: distribution of data
Inductive Bias
Inductive bias stands for the restrictions that are implied by the assumptions made in the learning method.
Or
An inductive bias of a learner is the set of additional assumptions sufficient to justify its inductive inferences as deductive inferences.
-Tom mitchell
Example:
Assumption: The solution to the problem of road safety can be expressed as a conjunction of a set of eight concepts.it does not allow for more complex expressions that cannot be written as conjunction. Here inductive bias means that there are some potential solutions that we cannot explore, and not contained within the version space that has to be examined.
In order to have an unbiased learner, the version space would have to contain every possible hypothesis that could possibly be expressed.
The solution that the learner produced could never be more general than the complete set of training data.
Similarly it is possible to classify data that learner had previously encountered (as the rote learner could) but would be unable to generalize in order to classify new, unseen data.
The inductive bias of the CEA (candidate elimination algorithm) is that it is only able to classify a new piece of data if all the hypotheses contained within its version space gives data the same classification.
Hence, the inductive bias does not impose a limitation on the learning method.
Key takeaway:
● Hypothesis space is the set of all the possible legal hypothesis.
● This is the set from which the machine learning algorithm will decide the best possible (only one) which would best represent the target function or the outputs.
● Inductive bias stands for the restrictions that are implied by the assumptions made in the learning method.
The issues can be handled by analysing the output of a machine learning model, which is an integral component of any data science project. Model evaluation aims to estimate the generalisation accuracy of a model on future (unseen/out-of-sample) results.
Methods for assessing a model’s efficiency are divided into 2 categories: respectively, holdout and Cross-validation. Both approaches use a test set (i.e data not seen by the model) to assess model efficiency. It’s not recommended to use the data we used to construct the model to test it. This is because our model will simply remember the entire training set, and will therefore always predict the correct label for any point in the training set.
Holdout
The aim of holdout evaluation is to test a model on different data than it was trained on. This offers an unbiased estimate of learning success.
In this approach, the dataset is randomly divided into three subsets:
● Training set
● Validation set
● Test set
Cross Validation
Cross-validation is a method that involves partitioning the original observation dataset into a training set, used to train the model, and an independent set used to test the analysis.
Cross-validation is a technique in which we train our model using the subset of the data-set and then test using the complementary subset of the dataset.
The three measures involved in cross-validation are as follows :
● Reserve any portion of sample data-set.
● Using the rest data-set train the model.
● Test the model using the reserve portion of the data-set.
Method of cross validation
Validation:
In this approach, we perform training on the 50 percent of the given data-set and rest 50 percent is used for the testing purpose. The major downside of this method is that we perform training on the 50 percent of the dataset, it which possible that the remaining 50 percent of the data contains some important information which we are leaving while training our model i.e higher bias.
LOOCV (Leave One Out Cross Validation)
In this process, we perform training on the whole data-set but leaves only one data-point of the available data-set and then iterates on each data-point. It has some benefits as well as drawbacks too.
A benefit of using this approach is that we make use of all data points and therefore it is low bias.
The main downside of this approach is that it leads to higher variance in the testing model as we are testing against one data point. If the data point is an outlier it may lead to higher variance. Another downside is it takes a lot of execution time as it iterates over ‘the amount of data points’ times.
K-Fold Cross Validation
In this process, we break the data-set into k number of subsets(known as folds) then we perform training on all the subsets but leave one(k-1) subset for the evaluation of the trained model. In this step, we iterate k times with a different subset reserved for testing purposes each time.
The most popular cross-validation technique is k-fold cross-validation, where the original dataset is partitioned into k equal size subsamples, called folds. The k is a user-specified number, usually with 5 or 10 as its preferred value.
Advantages of cross-validation:
● More precise estimation of out-of-sample accuracy.
● More “efficient” use of data as any observation is used for both training and testing.
Key takeaway:
● Cross-validation is a technique in which we train our model using the subset of the data-set and then test using the complementary subset of the dataset.
● It is often suggested that the value of k should be 10 as the lower value
k is taken towards validation and higher value of k leads to LOOCV process.
Optimization is the problem of finding a set of inputs to an objective function that results in a maximum or minimum function evaluation.
It is the daunting issue that underlies many machine learning algorithms, from fitting logistic regression models to training artificial neural networks.
There are perhaps hundreds of popular optimization algorithms, and perhaps tens of algorithms to choose from in popular science code libraries. This can make it difficult to know which algorithms to consider for a given optimization problem.
In this, you can discover a guided tour of various optimization algorithms.
You will know about:
● Optimization algorithms may be grouped into those that use derivatives and those that do not.
● Classical algorithms use the first and often second derivative of the objective function.
● Direct search and stochastic algorithms are developed for objective functions where function derivatives are inaccessible.
Optimization Algorithm
Optimization refers to a method for finding the input parameters or arguments to a function that result in the minimum or maximum output of the function.
The most popular type of optimization problems encountered in machine learning are continuous function optimization, where the input arguments to the function are real-valued numeric values, e.g. Floating point values. The performance from the function is also a real-valued evaluation of the input values.
We might refer to problems of this form as continuous function optimization, to differentiate from functions that take discrete variables and are referred to as combinatorial optimization problems.
There are many different types of optimization algorithms that can be used for continuous function optimization problems, and maybe just as many ways to group and summarise them.
One approach to grouping optimization algorithms is based on the amount of knowledge available about the target function that is being optimised that, in turn, can be used and harnessed by the optimization algorithm.
Generally, the more information that is available about the target function, the simpler the function is to optimise if the information can easily be used in the search.
Perhaps the main division in optimization algorithms is whether the objective function can be distinguished at a point or not. That is, whether the first derivative (gradient or slope) of the function can be determined for a given candidate solution or not. This partitions algorithms into those that can make use of the measured gradient information and those that do not.
Key takeaway:
● Optimization is the problem of finding a set of inputs to an objective function that results in a maximum or minimum function evaluation.
● this is not an exhaustive coverage of algorithms for continuous function optimization, but it does cover the main approaches that you are likely to find as a frequent practitioner.
References:
- Machine Learning. Tom Mitchell. First Edition, McGraw- Hill, 1997
- Understanding Machine Learning. Shai Shalev-Shwartz and Shai Ben-David. Cambridge University Press. 2017. [SS-2017]