Unit - 3

Context Free Grammar (CFG) and Context Free Language (CFL)

3.1 Basic Elements of Grammar

It is a set of finite formal rules for generating syntactically or semantically accurate phrases.

Elements

Grammar is made up of two basic elements —

1. Terminal symbol

Terminal symbols are the components of sentences created by a grammar and are represented by small case letters such as a, b, c, and so on.

2.     Non - terminal symbol

Non-Terminal Symbols are symbols that are used in the construction of a sentence but are not part of the sentence. Auxiliary Symbols and Variables are other names for Non-Terminal Symbols. A capital letter, such as A, B, or C, is used to symbolize these symbols.

Formal definition

<N, T, P, S> are four tuples that can be used to express any grammar.

N — non-terminal symbols in a finite non-empty set.

T — Terminal Symbols in a Finite Set.

P — Non-Empty Finite Set of Production Rules.

S — Start Symbol (Symbol from where we start producing our sentences or strings).

3.2 Formal Definition of Context Free Grammar

Context-free grammar (CFG) is a collection of rules (or productions) for recursive rewriting used to produce string patterns.

It consists of:

●      a set of terminal symbols,

●      a set of non-terminal symbols,

●      a set of productions,

●      a start symbol.

Context-free grammar G can be defined as:

G = (V, T, P, S)

Where 

G - grammar, used for generate string,

V - final set of non-terminal symbol, which are denoted by capital letters,

T - final set of terminal symbol, which are denoted be small letters,

P - set of production rules, it is used for replacing non terminal symbol of a string in both side (left or right)

S - start symbol, which is used for derive the string

A CFG for Arithmetic Expressions -

An example grammar that generates strings representing arithmetic expressions with the four operators +, -, *, /, and numbers as operands is:

1. <expression> --> number

2. <expression> --> (<expression>)

3.<expression> --> <expression> +<expression>

4. <expression> --> <expression> - <expression>

5. <expression> --> <expression> * <expression>

6. <expression> --> <expression> / <expression>

The only non-terminal symbol in this grammar is <expression>, which is also the

Start symbol. The terminal symbols are {+, -, *, /, (,), number}

●      The first rule states that an <expression> can be rewritten as a number.

●      The second rule says that an <expression> enclosed in parentheses is also an <expression>

●      The remaining rules say that the sum, difference, product, or division of two <expression> is also an expression.

Key takeaway

1. CFG is a collection of rules (or productions) for recursive rewriting used to produce string patterns.

3.3 Sentential form

A partial derivation tree is a subtree of a derivation tree/parse tree that contains either all of its offspring or none of them.

Example

If the productions in any CFG are

S → AB, A → aaA | ε, B → Bb| ε

The following is an example of a partial derivation tree:

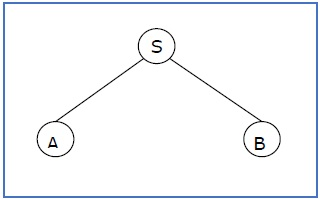
Fig 1: Example

A sentential form is a partial derivation tree that contains the root S. The sub-tree on the right is also in sentential form.

A sentential form is any string derivable from the start symbol. Thus, in the derivation of a + a * a, E + T * F and E + F * a and F + a * a are all sentential forms as are E and a + a * themselves.

3.4 Derivation and Derivation Tree/ Parse Tree

Suppose we have a context free grammar G with production rules:

S->aSb|bSa|SS|ɛ

Left most derivation (LMD) and Derivation Tree:

Leftmost derivation of a string from staring symbol S is done by replacing leftmost

Non-terminal symbol by RHS of corresponding production rule.

For example:

The leftmost derivation of string abab from grammar G above is done as:

S =>aSb =>abSab =>abab

The symbols in bold are replaced using production rules.

Derivation tree: It explains how string is derived using production rules from S and

Is shown in Figure.

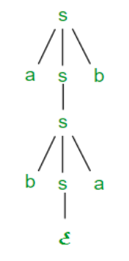
Fig 2: Derivation tree

Right most derivation (RMD):

It is done by replacing rightmost non-terminal symbol S by RHS of corresponding production rule.

For Example: The rightmost derivation of string abab from grammar G above

Is done as:

S =>SS =>SaSb =>Sab =>aSbab =>abab

The symbols in bold are replaced using production rules.

The derivation tree for abab using rightmost derivation is shown in Figure.

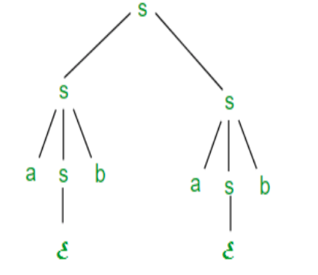
Fig 3: Right most derivation

A derivation can be either LMD or RMD or both or none.

For Example:

S =>aSb =>abSab =>abab is LMD as well as RMD But

S => SS =>SaSb =>Sab =>aSbab =>abab is RMD but not LMD.

Parse tree

​​A parse tree is an entity which represents the structure of the derivation of a

Terminal string from some non-terminal.

●      The graphical representation of symbols is the Parse tree. Terminal or non-terminal may be the symbol.

●      In parsing, using the start symbol, the string is derived. The starter symbol is the root of the parse tree.

●      It is the symbol's graphical representation, which can be terminals or non-terminals.

●      The parse tree follows operators' precedence. The deepest sub-tree went through first. So, the operator has less precedence over the operator in the sub-tree in the parent node.

Key features to define are the root ∈ V and yield ∈ Σ * of each tree.

●      For each σ ∈ Σ, there is a tree with root σ and no children; its yield is σ

●      For each rule A → ε, there is a tree with root A and one child ε; its yield is ε

●      If t 1, t 2, ..., t n are parse trees with roots r 1, r 2, ..., r n and respective yields y 1, y 2,..., y n , and A → r 1 r 2 ...r n  is a production, then there is a parse tree with root A whose children are t 1, t 2, ..., t n . Its root is A and its yield is the concatenation of yields: y 1 y 2 ...y n

Here, parse trees are constructed from bottom up, not top down.

The actual construction of “adding children” should be made more precise, but we intuitively know what’s going on.

As an example, here are all the parse (sub) trees used to build the parse tree

For the arithmetic expression 4 + 2 * 3 using the expression grammar

E → E + T | E - T | T

T → T * F | F

F → a | (E)

Where a represents an operand of some type, be it a number or variable. The

Trees are grouped by height.

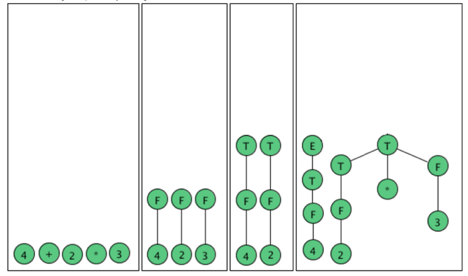
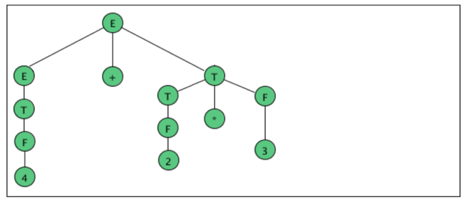
Fig 4: Example of parse tree

Parse Trees and Derivations

A derivation is a sequence of strings in V * which starts with a non-terminal

In V-Σ and ends with a string in Σ *.

Let’s consider the sample grammar

E → E+E | a

We write:

E ⇒ E+E ⇒ E+E+E ⇒a+E+E⇒a+a+E⇒a+a+a

But this is incomplete, because it doesn’t tell us where the replacement rules are

Applied.

We actually need strings which indicate which non-terminal is replaced in all but the first and last step:

E ⇒ Ě+E ⇒ Ě+E+E ⇒a+Ě+E ⇒a+a+Ě ⇒a+a+a

In this case, the marking is only necessary in the second step; however it is crucial,

Because we want to distinguish between this derivation and the following one:

E ⇒ E+Ě ⇒ Ě+E+E ⇒a+Ě+E ⇒a+a+Ě ⇒a+a+a

We want to characterize two derivations as “coming from the same parse tree.”

The first step is to define the relation among derivations as being “more left-oriented at one step”. Assume we have two equal length derivations of length n > 2:

D: x 1 ⇒ x 2 ⇒ ... ⇒x n

D′: x 1 ′ ⇒ x 2 ′ ⇒ ... ⇒x n ′

Where x 1 = x 1 ′ is a non-terminal and

x n = x n ′ ∈ Σ *

Namely they start with the same non-terminal and end at the same terminal string

And have at least two intermediate steps.

Let’s say D < D′ if the two derivations differ in only one step in which there are 2 non-

Terminals, A and B, such that D replaces the left one before the right one and D′ does the opposite. Formally:

D < D′ if there exists k, 1 &lt; k &lt; n such that

x i = x i ′ for all i ≠ k (equal strings, same marked position)

x k-1 = uǍvBw, for u, v, w ∈ V*

x k-1 ′ = uAvB̌w, for u, v, w ∈ V*

x k =uyvB̌w, for production A → y

x k ′ = uǍvzw, for production B → z

x k+1 = x k+1 ′ = uyvzw (marking not shown)

Two derivations are said to be similar if they belong to the reflexive, symmetric, transitive closure of <.

Key takeaway:

1. In parsing, using the start symbol, the string is derived. The starter symbol is the root of the parse tree.
2. The graphical representation of symbols is the Parse tree. Terminal or non-terminal may be the symbol.

3.5 Context Free Language (CFL)

A context-free language (CFL) is a language developed by context-free grammar (CFG) in formal language theory. In programming languages, context-free languages have many applications, particularly most arithmetic expressions are created by context-free grammars.

●      Through comparing different grammars that characterize the language, intrinsic properties of the language can be separated from extrinsic properties of a particular grammar.

●      In the parsing stage, CFLs are used by the compiler as they describe the syntax of a programming language and are used by several editors.

A grammatical description of a language has four essential components -

1. There is a set of symbols that form the strings of the language being defined. They are called terminal symbols, represented by V t.
2. There is a finite set of variables, called non-terminals. These are represented by V n.
3. One of the variables represents the language being defined; it is called the start symbol. It is represented by S.
4. There are a finite set of rules called productions that represent the recursive definition of a language. Each production consists of:

●      A variable that is being defined by the production. This variable is also called the production head.

●      The production symbol ->

●      A string of zero terminals and variables, or more.

Key takeaway

1. ​​CFL is a language developed by context-free grammar (CFG) in formal language theory.

3.6 Ambiguous Grammar

●      A context free grammar is called ambiguous if there exists more than one

LMD or RMD for a string which is generated by grammar.

●      There will also be more than one derivation tree for a string in ambiguous grammar.

●      The grammar described above is ambiguous because there are two derivation Trees.

●      There can be more than one RMD for string abab which are:

S =>SS =>SaSb =>Sab =>aSbab =>abab

S =>aSb =>abSab =>abab

3.7 Writing grammar for language

The collection of all strings created from a grammar G is represented by its corresponding language L(G). Consider the grammar in the following example:

G: S-> aSb|ε

We can produce using S-> in this grammar. As a result, is a part of L. (G). Similarly, ab is created using S=>aSb=>ab. Aabb can be created in the same way.

Therefore,

L(G) = {anbn, n>=0}

The condition n = 0 is regarded to be accepted in the above-mentioned language L(G).

3.8 Simplification of CFG: Eliminating Є-productions

As we have included, context-free grammar can effectively represent different languages. Not all grammar is always optimized, which means that there might be some extra symbols in the grammar (non-terminal). Unnecessary change in the length of grammar with additional symbols.

Here are the properties of reduced grammar:

1. Every parameter (i.e., non-terminal) and every terminal of G occurs in the derivation of any word in L.
2. As X→Y where X and Y are non-terminal, there should not be any output.
3. If ε is not in the L language, then the X→ ε output does not have to be.

Let’s see the simplification process

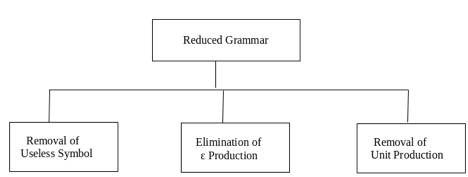
Fig 5: Simplification process

●      Elimination of ε Production - The Type S → ε productions are called ε productions. Only those grammars which do not produce ε can be excluded from these types of output.

Step 1: First find all nullable non-terminal variables which derive ε.

Step 2: Create all output A → x for each production A →a where x is extracted from a by removing one or more non-terminals from step 1.

Step 3: Now combine with the original output the outcome of step 2 and delete ε productions.

Example:  Remove the production from the given CFG

1. E → XYX 
2. X → 0X | ε 
3. Y → 1Y | ε

Solution:

Now, we remove the rules X → ε and Y → ε while removing ε production. In order to maintain the sense of CFG, whenever X and Y appear, we actually position ε on the right-hand side.

Let’s see

If the 1st X at right side is ε, then

E → YX

Similarly, if the last X in right hand side is ε, then

E → XY

If Y = ε, then

E → XX

If Y and X are ε then,

S → X

If both X are replaced by ε

E → Y 

Now,

E → XY | YX | XX | X | Y

Now let us consider

X → 0X 

If we then put ε for X on the right-hand side,

X → 0

X → 0X | 0 

Similarly, Y → 1Y | 1

Collectively, with the ε output excluded, we can rewrite the CFG as

E → XY | YX | XX | X | Y 

X → 0X | 0 

Y → 1Y | 1

Key takeaways:

1. Grammar simplification means reducing grammar by the elimination of useless symbols.
2. Simplification process contains three major parts.
3. Removal of useless symbol, Elimination of ε production, Removing unit production

3.9 Unit productions

Unit productions are those productions in which another non-terminal generates a non-terminal one.

To remove production unit, follow given steps: →

Step 1: To delete X → Y, when Y→ a occurs in the grammar, apply output X → a to the grammar law.

Step 2: Remove X → Y from the grammar now.

Step 3: Repeat steps 1 and 2 until all unit output is deleted.

Example:

1. E → 0X | 1Y | Z 
2. X → 0E | 00 
3. Y → 1 | X 
4. Z → 01

Sol:

E → Z is a unit production. But while removing E → Z, we have to consider what Z gives. So, we can add a rule to E.

E → 0X | 1Y | 01 

Similarly, Y → X is also a unit production so we can modify it as

Y → 1 | 0S | 00 

Finally, then without unit manufacturing, we can write CFG as

E → 0X | 1Y | 01 

X → 0E | 00 

Y → 1 | 0S | 00 

Z → 01 

3.10 Useless production, and useless symbols

A symbol can be useless if it does not appear on the right-hand side of the production rule and is not involved in the derivation of any string.  The symbol is regarded as a symbol which is useless. Likewise, if it does not participate in the derivation of any string, a variable may be useless. That variable is called a useless symbol.

Useless symbols

If a variable X in a context-free grammar does not appear in any derivation of a word from that grammar, it is said to be useless.

This is a simple algorithm for removing superfluous variables from CFGs.

If a variable generates a string of terminals, call it generating. It's worth noting that a context-free grammar accepts language that isn't empty if and only if the start sign is generated. An algorithm for locating the generating variables in a CFG is as follows:

1. If a variable X has a production X -> w, where w is a string of solely terminals and/or variables already tagged "producing," mark it as “generating."
2. Repeat the previous step until no more variables are designated as “producing.”

All variables that aren't labeled "generating" are non-generating variables (by a simple induction on the length of derivations).

If the start symbol yields a string containing the variable, call it accessible. Here's how to identify the variables that can be reached in a CFG:

Assign the status "reachable" to the start variable.

1. If there is a production X -> w, where X is a variable previously tagged as "reachable" and w is a string containing Y, mark a variable Y as “reachable."
2. Repeat the last step until no more variables are identified as "reachable."

All variables that aren't labeled "reachable" are unavailable (by a simple induction on the length of derivations).

Keep in mind that a CFG only has no useless variables if and only if all of its variables are reachable and producing.

As a result, it is possible to remove unnecessary variables from a grammar in the following way:

1. Find and eliminate all non-generating variables, as well as any productions involving non-generating variables.
2. Find and delete any non-reachable variables in the resulting grammar, as well as all products that use non-reachable variables.

Step 1 does not make other variables non-generating or non-reachable, and step 2 does not make other variables non-generating or non-reachable. As a result, the end result is a grammar that is reachable and generates all variables, making it usable.

Key takeaway

1. If a variable X in a context-free grammar does not appear in any derivation of a word from that grammar, it is said to be useless.
2. This is a simple algorithm for removing superfluous variables from CFGs.

3.11 Normal Forms: Chomsky Normal Form, Greibach Normal Form

Chomsky normal forms

A context free grammar (CFG) is in Chomsky Normal Form (CNF) if all production

Rules satisfy one of the following conditions:

A non-terminal generating a terminal (e.g.; X->x)

A non-terminal generating two non-terminals (e.g.; X->YZ)

Start symbol generating ε. (e.g.; S->ε)

Consider the following grammars,

G1 = {S->a, S->AZ, A->a, Z->z}

G2 = {S->a, S->aZ, Z->a}

The grammar G1 is in CNF as production rules satisfy the rules specified for

CNF. However, the grammar G2 is not in CNF as the production rule S->aZ contains

Terminal followed by non-terminal which does not satisfy the rules specified for CNF.

Greibach normal forms

A CFG is in Greibach Normal Form if the Productions are in the following forms −

A → b

A → bD 1 …D n

S → ε

Where A, D 1 ,....,D n are non-terminals and b is a terminal.

Algorithm to Convert a CFG into Greibach Normal Form

Step 1 − If the start symbol S occurs on some right side, create a new start

Symbol S’ and a new production S’ → S.

Step 2 − Remove Null productions.

Step 3 − Remove unit productions.

Step 4 − Remove all direct and indirect left-recursion.

Step 5 − Do proper substitutions of productions to convert it into the proper form of

GNF.

Problem

Convert the following CFG into CNF

S → XY | Xn | p

X → mX | m

Y → Xn | o

Solution

Here, S does not appear on the right side of any production and there are no unit or

Null productions in the production rule set. So, we can skip Step 1 to Step 3.

Step 4

Now after replacing

X in S → XY | Xo | p

With

MX | m

We obtain

S → mXY | mY | mXo | mo | p.

And after replacing

X in Y → X n | o

With the right side of

X → mX | m

We obtain

Y → mXn | mn | o.

Two new productions O → o and P → p are added to the production set and then

We came to the final GNF as the following −

S → mXY | mY | mXC | mC | p

X → mX | m

Y → mXD | mD | o

O → o

P → p

Key takeaway:

1. CNF is a pre-processing step used in various algorithms.
2. For generation of string x of length ‘m’, it requires ‘2m-1’ production or steps in CNF.

3.12 Pumping Lemma for CFG

Lemma:

The language L = {anbncn | n ≥ 1} is not context free.

Proof (By contradiction)

Assuming that this language is context-free; hence it will have a context-free

Grammar.

Let K be the constant of the Pumping Lemma.

Considering the string akbkck, where L is length greater than K.

By the Pumping Lemma this is represented as uvxyz, such that all uvixyiz are also

In L, which is not possible, as:

Either v or y cannot contain many letters from {a, b, c}; else they are in the wrong

Order.

If v or y consists of a’s, b’s or c’s, then uv2xy2z cannot maintain the balance

Amongst the three letters.

Lemma:

The language L = {aibjck | i < j and i < k} is not context free.

Proof (By contradiction)

Assuming that this language is context-free; hence it will have a context-free grammar.

Let K be the constant of the Pumping Lemma.

Considering the string akbk+1ck+1, which is L > K.

By the Pumping Lemma this must be represented as uvxyz, such that all are also

In L.

-As mentioned previously neither v nor y may contain a mixture of symbols.

-Suppose consists of a’s.

Then there is no way y cannot have b’s and c’s. It generates enough letters to keep

Them more than that of the a’s (it can do it for one or the other of them, not both)

Similarly, y cannot consist of just a’s.

-So, suppose then that v or y contains only b’s or only c’s.

Consider the string uv0xy0z which must be in L. Since we have dropped both

v and y, we must have at least one b’ or one c’ less than we had in uvxyz, which

Was akbk+1ck+1. Consequently, this string no longer has enough of either b’s or c’s to be a member of L.

3.13 Closure properties of CFL

They are closed under −

●      Union

●      Concatenation

●      Kleene Star operation

Union of the languages A1 and A2, A = A1 A2 = {anbncmdm}

The additional development would have the corresponding grammar G, P:  S → S1 S2

Union

Let A1 and A2 be two context free languages. Then A1 ∪ A2 is also context free.

Example

Let A1 = {xn yn, n ≥ 0}. Corresponding grammar G 1 will have P: S1 → aAb|ab

Let A2 = {cm dm, m ≥ 0}. Corresponding grammar G 2 will have P: S2 → cBb| ε

Union of A1 and A2, A = A1 ∪ A2 = {xn yn} ∪ {cm dm}

The corresponding grammar G will have the additional production S → S1 | S2

Note - So under Union, CFLs are closed.

Concatenation

If A1 and A2 are context free languages, then A1 A2 is also context free.

Example

Union of the languages A 1 and A 2, A = A 1 A 2 = {an bn cm dm}

The corresponding grammar G will have the additional production S → S1 S2

Note - So under Concatenation, CFL are locked.

Kleene Star

If A is a context free language, so that A* is context free as well.

Example

Let A = {xn yn, n ≥ 0}. G will have corresponding grammar P: S → aAb| ε

Kleene Star L 1 = {xn yn}*

The corresponding grammar G 1 will have additional productions S1 → SS 1 | ε

Note - So under Kleene Closure, CFL's are closed.

Context-free languages are not closed under −

●      Intersection − If A1 and A2 are context free languages, then A1 ∩ A2 is not necessarily context free.

●      Intersection with Regular Language − If A1 is a regular language and A2 is a context free language, then A1 ∩ A2  is a context free language.

●      Complement − If A1 is a context free language, then A1’ may not be context free.

3.14 Decision properties of CFL

●      It is possible to determine whether or not a CFG G is empty.

●      The following questions are undecidable?

●      Testing the membership of a string w in a CFG G is also decidable.

1. Is there any ambiguity in a particular G?

2. Is a CFL by definition ambiguous?

3. Is the point where two CFLs meet empty?

4. Is there a difference between two CFLs?

3.15 Chomsky Hierarchy

The Chomsky Hierarchy describes the class of languages that the various machines embrace. The language group in Chomsky's Hierarchy is as follows:

1. Type 0 known as Unrestricted Grammar.
2. Type 1 known as Context Sensitive Grammar.
3. Type 2 known as Context Free Grammar.
4. Type 3 Regular Grammar.

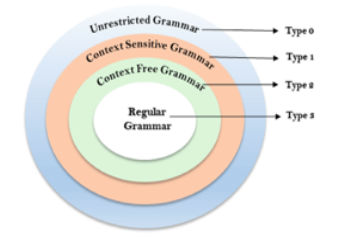
Fig 6: Chomsky hierarchy

The above diagram shows the hierarchy of Chomsky. Each language of type 3 is therefore also of type 2, 1 and 0 respectively. Similarly, every language of type 2 is also of type 1 and type 0 likewise.

●      Type 0 grammar -

Type 0 grammar is known as Unrestricted grammar. The grammar rules of these types of languages are unregulated. Turing machines can model these languages efficiently.

Example:

1. BAa → aa 
2. P → p 

●      Type 1 grammar -

Type 1 grammar is known as Context Sensitive Grammar. Context-sensitive grammar is used to describe language that is sensitive to context. The context-sensitive grammar follows the rules below:

●      There may be more than one symbol on the left side of their development rules for context-sensitive grammar.

●      The number of left-hand symbols does not surpass the number of right-hand symbols.

●      The A → ε type rule is not permitted unless A is a beginning symbol. It does not occur on the right-hand side of any rule.

●      The Type 1 grammar should be Type 0. Production is in the form of V →T in type1

Example:

1. S → AT 
2. T → xy 
3. A → a

●      Type 2 grammar -

Type 2 Grammar is called Context Free Grammar. Context free languages are the languages which can be represented by the CNF (context free grammar) Type 2 should be type 1. The production rule is:

A → α

Example:

1. A → aBb 
2. A → b 
3. B → a 

●      Type 3 grammar -

Type 3 Grammar is called Regular Grammar. Those languages that can be represented using regular expressions are regular languages. These languages may be NFA or DFA-modelled.

Type3 has to be in the form of -

V → T*V / T*

Example:

A → xy 

Key takeaway:

1. Where the number of symbols in V is equal to or less than T
2. Where A is any single non-terminal and is any combination of terminals and non-terminals.
3. The most limited form of grammar is Type3. Type2 and Type1 should be the grammar of Type3.

3.16 Cock-Younger-Kasami Algorithm

Itiroo Sakai developed the Cocke–Younger–Kasami algorithm (also known as CYK or CKY) in 1961 as a parsing algorithm for context-free grammars. John Cocke, Daniel Younger, Tadao Kasami, and Jacob T. Schwartz are some of the algorithm's rediscoverers. Bottom-up parsing and dynamic programming are used.

The standard version of CYK only works with Chomsky normal form context-free grammars (CNF). Any context-free grammar, on the other hand, can be turned (by convention) into a CNF grammar that expresses the same language.

The importance of the CYK algorithm stems from its high efficiency in certain situations. Using Big O notation, the worstcase running time of CYK is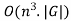 , where n is the length of the parsed string and 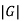is the size of the CNF grammar G. This makes it one of the most efficient parsing algorithms in terms of worst-case asymptotic complexity, although other algorithms exist with better average running time in many practical scenarios.

Algorithm

The algorithm in pseudocode is as follows:

Let the input be a string I consisting of n characters: a1 ... an.

Let the grammar contain r nonterminal symbols R1 ... Rr, with start symbol R1.

Let P [n, n, r] be an array of booleans. Initialize all elements of P to false.

For each s = 1 to n

For each unit production Rv → as

Set P [1, s, v] = true

For each l = 2 to n -- Length of span

For each s = 1 to n-l+1 -- Start of span

For each p = 1 to l-1 -- Partition of span

For each production Ra    → Rb Rc

If P [p, s, b] and P [l-p, s+p, c] then set P [l, s, a] = true

If P[n,1,1] is true then

I is member of language

Else

I is not member of language

References:

1. John E. Hopcroft, Rajeev Motwani, Jeffrey D.Ullman, “Introduction to Automata Theory Languages and Computation”, Addison-Wesley, ISBN 0-201-44124-1
2. Sanjeev Arora and Boaz Barak, “Computational Complexity: A Modern Approach”, Cambridge University Press, ISBN: 0521424267 97805214242643
3. John Martin, “Introduction to Languages and The Theory of Computation”, 2nd Edition, McGrawHill Education, ISBN-13: 978-1-25-900558-9, ISBN-10: 1-25-900558-5
4. J.Carroll & D Long, “Theory of Finite Automata”, Prentice Hall, ISBN 0-13-913708-45.