Unit - 4
Pushdown Automata (PDA)
It is a way to implement context-free grammar as we design DFA for regular grammar. A DFA can remember a finite amount of information, but a PDA can remember an infinite amount of information.
Basically, a pushdown automaton is -
“Finite state machine” + “a stack”
A pushdown automaton has three components −
● an input tape,
● a control unit, and
● a stack with infinite size.
The stack head scans the top symbol of the stack.
A stack does two operations −
● Push − a new symbol is added at the top.
● Pop − the top symbol is read and removed.
A PDA may or may not read an input symbol, but it has to read the top of the stack in
Every transition.
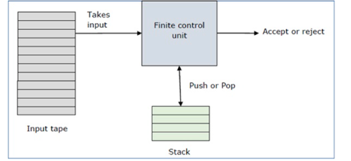
Fig1: Basic structure of PDA
A PDA can be formally described as a 7-tuple (Q, ∑, S, δ, q 0, I, F) −
Where,
● Q is the finite number of states
● ∑ is input alphabet
● S is stack symbols
● δ is the transition function: Q × (∑ ∪ {ε}) × S × Q × S*)
● q 0 is the initial state (q 0 ∈ Q)
● I is the initial stack top symbol (I ∈ S)
● F is a set of accepting states (F ∈ Q)
The following diagram shows a transition in a PDA from a state q 1 to state q 2, labeled as a, b → c −

Fig 2: Example
This means at state q1, if we encounter an input string ‘a’ and the top symbol of the stack is ‘b’, then we pop ‘b’, push ‘c’ on top of the stack and move to state q2.
Key takeaway
It is a way to implement context-free grammar as we design DFA for regular grammar. A DFA can remember a finite amount of information, but a PDA can remember an infinite amount of information.
When a PDA accepts a string in final state acceptability, the PDA is in a final state after reading the full string. We can make moves from the starting state to a final state with any stack values. As long as we end up in a final state, the stack values don't matter.
If the PDA enters any final state in zero or more moves after receiving the complete input, it is said to accept it by the final state.
Let P = (Q, ∑, Γ, δ, q0, Z, F) be a PDA. The language acceptable by the final state can be defined as:
L(PDA) = {w | (q0, w, Z) ⊢* (p, ε, ε), q ∈ F}
Equivalence of Acceptance by Final State and Empty Stack
There is a PDA P2 such that L = L (P2) if L = N(P1) for some PDA P1. That is, the language supported by the empty stack PDA will be supported by the end state PDA as well.
Empty stack
If a language L = L (P1) exists for a PDA P1, then L = N (P2) exists for a PDA P2. That is, language supported by the end state PDA is also supported by the empty stack PDA.
The stack of PDAs becomes empty after reading the input string from the initial setup for some PDA.
When a PDA has exhausted its stack after reading the entire string, it accepts a string.
Let P = (Q, ∑, Γ, δ, q0, Z, F) be a PDA. The language acceptable by empty stack can be defined as:
N(PDA) = {w | (q0, w, Z) ⊢* (p, ε, ε), q ∈ Q}
Example
Construct a PDA that accepts L = {0n 1n | n ≥ 0}
Solution:

This language accepts L = {ε, 01, 0011, 000111, ............................. }
The number of ‘a' and ‘b' in this example must be the same.
● We began by inserting the special symbol ‘$' into the empty stack.
● If we encounter input 0 and top is Null at state q2, we push 0 into the stack. It's possible that this will happen again. We pop this 0 if we meet input 1 and top is 0.
● If we encounter input 1 at state q3 and the top is 0, we pop this 0. It's possible that this will continue to iterate. We pop the top element if we meet input 1 and top is 0.
● If the special symbol '$' appears at the top of the stack, it is popped out, and the stack eventually moves to the accepting state q4.
The non-deterministic pushdown automata is very much similar to NFA. We will
Discuss some CFGs which accept NPDA.
The CFG which accepts deterministic PDA accepts non-deterministic PDAs as well.
Similarly, there are some CFGs which can be accepted only by NPDA and not by
DPDA. Thus, NPDA is more powerful than DPDA.
Example:
Design PDA for Palindrome strips.
Solution:
Suppose the language consists of string L = {aba, aa, bb, bab, bbabb, aabaa, ......].
The string can be an odd palindrome or even a palindrome. The logic for constructing PDA is that we will push a symbol onto the stack till half of the string then we will read each symbol and then perform the pop operation. We will compare to see whether the symbol which is popped is similar to the symbol which is read. Whether we reach the end of the input, we expect the stack to be empty.
This PDA is a non-deterministic PDA because finding the mid for the given string and
Reading the string from the left and matching it with the right (reverse) direction leads to non-deterministic moves.
Here is the ID.

Simulation of abaaba
1. δ(q1, abaaba, Z) Apply rule 1
2. δ(q1, baaba, aZ) Apply rule 5
3. δ(q1, aaba, baZ) Apply rule 4
4. δ(q1, aba, abaZ) Apply rule 7
5. δ(q2, ba, baZ) Apply rule 8
6. δ(q2, a, aZ) Apply rule 7
7. δ(q2, ε, Z) Apply rule 11
8. δ(q2, ε) Accept
Key takeaway
- The non-deterministic pushdown automata is very much similar to NFA. We will discuss some CFGs which accept NPDA.
- The CFG which accepts deterministic PDA accepts non-deterministic PDAs as well.
We can design a similar nondeterministic PDA that accepts the language produced by the context-free grammar G if it is context-free. For the grammar G, a parser can be created.
In addition, if P is a pushdown automaton, an analogous context-free grammar G can be built.
L(G) = L(P)
Algorithm to find PDA corresponding to a given CFG
Input − A CFG, G = (V, T, P, S)
Output − Equivalent PDA, P = (Q, ∑, S, δ, q0, I, F)
Step1 - Convert the CFG's productions into GNF.
Step2 - There will be only one state q on the PDA.
Step3 - The CFG's start symbol will be the PDA's start sign.
Step4 - The PDA's stack symbols will be all of the CFG's non-terminals, and the PDA's input symbols will be all of the CFG's terminals.
Step5 - For each production in the form A → aX where a is terminal and A, X are a combination of terminal and non-terminals, make a transition δ (q, a, A).
Problem
Construct a PDA using the CFG below.
G = ({S, X}, {a, b}, P, S)
Where are the productions?
S → XS | ε, A → aXb | Ab | ab
Solution
Let's say you have a PDA that's equivalent to that.
P = ({q}, {a, b}, {a, b, X, S}, δ, q, S)
Where δ −
δ(q, ε , S) = {(q, XS), (q, ε )}
δ(q, ε , X) = {(q, aXb), (q, Xb), (q, ab)}
δ(q, a, a) = {(q, ε )}
δ(q, 1, 1) = {(q, ε )}
Algorithm to find CFG corresponding to a given PDA
Input − A CFG, G = (V, T, P, S)
Output − Equivalent PDA, P = (Q, ∑, S, δ, q0, I, F) such that the non- terminals of the grammar G will be {Xwx | w,x ∈ Q} and the start state will be Aq0,F.
Step1 − For every w, x, y, z ∈ Q, m ∈ S and a, b ∈ ∑, if δ (w, a, ε) contains (y, m) and (z, b, m) contains (x, ε), add the production rule Xwx → a Xyzb in grammar G.
Step2 − For every w, x, y, z ∈ Q, add the production rule Xwx → XwyXyx in grammar G.
Step3 − For w ∈ Q, add the production rule Xww → ε in grammar G.
Key takeaway
- The language L(G) that corresponds to a given grammar G is unique.
- All strings that can be created from grammar G must be represented in the language L(G).
- There must be no strings that cannot be created from G in the language L(G) that corresponds to grammar G.
The power of a CFG and a PDA is the same: a CFG generates context-free language, while a PDA recognizes context-free language.
We demonstrate how to transform a CFG into a PDA that recognizes the CFG's language and vice versa.
Application: Because of this equivalence, a CFG can be used to specify a programming language, and the equivalent PDA can be used to construct the language's compiler.
Theorem: If a pushdown automaton recognizes a language, it is context-free.
This means that:
1. If a language L is context-free, it is recognized by a PDA ML.
2. If a PDA ML recognizes a language L, there is a CFG GL that generates L.
Lemma: If a language is context-free, it will be recognized by a pushdown automaton.
Proof concept:
1. Let's A pretend to be a CFL. We know from the definition that A has a CFG G that it generates.
2. We'll demonstrate how to transform G, PDA P into one that accepts strings ພ if G it creates ພ.
3. P will start by figuring out a derivation ພ.

Deterministic context-free languages (DCFL) are a subset of context-free languages in formal language theory. They are the context-free languages that a deterministic pushdown automaton can accept. DCFLs are always unambiguous, which means they accept a clear grammar. Unambiguous CFLs can be non-deterministic, hence DCFLs are a subset of unambiguous CFLs.
Because DCFLs may be parsed in linear time and various constrained variants of DCFGs admit easy practical parsers, they are of tremendous practical interest. As a result, they're commonly employed in computer science.
The deterministic pushdown automaton is strongly connected to the DCFL concept (DPDA). When we make pushdown automatons deterministic, their language power is decreased to the point where they are unable to pick between distinct state-transition options and, as a result, cannot identify any context-free languages. A DCFL is not always generated by unambiguous grammars.
The language of even-length palindromes on the 0 and 1 alphabet, for example, has the unambiguous context-free grammar S → 0S0 | 1S1 | ε. Because an arbitrary string of this language cannot be parsed without first reading all of its letters, a pushdown automaton must experiment with different state transitions to account for the various lengths of a semi-parsed string.
Properties
In polynomial time and O (log2 n) space, a deterministic Turing computer can recognize deterministic context-free languages; as a corollary, DCFL is a subset of the complexity class SC.
The following operations close the set of deterministic context-free languages:
● Complement
● Inverse homomorphism
● Right quotient with a regular language
● Pre: pre(L) is the subset of all strings that have a proper prefix and are also part of display style L.
● Min: min (L) is the subset of all strings in display style L that do not have a suitable prefix.
● Max: max (L) is the subset of all strings in display style L that are not the prefix of a longer string.
Importance
This class of languages has a lot of practical value in computer science since they can be parsed significantly faster than non-deterministic context-free languages. A deterministic pushdown automaton's program complexity and execution time are significantly lower than those of a nondeterministic one. When a nondeterministic step happens in the naive implementation, the latter must make copies of the stack.
Valiant's algorithm is the most well-known algorithm for testing membership in any context-free language, and it takes O (n2.378) time, where n is the length of the string. An LR(k) parser, on the other hand, can accept deterministic context-free languages in O(n) time. This is very important for computer language translation because many computer languages belong to this class of languages.
Key takeaway
- Deterministic context-free languages (DCFL) are a subset of context-free languages in formal language theory.
- They are the context-free languages that a deterministic pushdown automaton can accept.
- DCFLs are always unambiguous, which means they accept a clear grammar.
- The deterministic pushdown automaton is strongly connected to the DCFL concept (DPDA).
References:
- Daniel Cohen, “Introduction to Computer Theory”, Wiley & Sons, ISBN 97881265133454
- Kavi Mahesh, “Theory of Computation: A Problem-Solving Approach”, Wiley India, ISBN1081265331106
- Michael Sipser, “Introduction to the Theory of Computation”, Cengage Learning, ISBN-13: 97811331878137
- Vivek Kulkarni, “Theory of Computation”, Oxford University Press, ISBN 0-19-808458