Unit - 5
Turing Machines (TM)
An information processing system (TM) may be a mathematical model that consists of
Associate infinite length tape divided into cells on which input is given. It consists of a head that reads the input tape.
A state register stores the state of the information processing system. Once reading an associated input image, it’s replaced with another image, its internal state is modified, and it moves from one cell to the proper or left. If the metal reaches the ultimate state, the input string is accepted, otherwise rejected.
Formal definition
A metal will be formally delineate as a 7-tuple (Q, X, ∑, δ, q0, B, F)
Where −
• Q may be a finite set of states
• X is that the tape alphabet
• ∑ is that the input alphabet
• δ may be a transition function; δ: alphabetic character × X → alphabetic character × X ×
• q0 is that the initial state
• B is that the blank image
• F is that the set of ultimate states
Basic model of Turing machine
With the help of the following representation, the turning machine can be modelled.
- The input tape contains an infinite number of cells, each cell containing one input symbol, so it is possible to position the input string on the tape. Blank characters fill up the empty tape.

Fig 1: Input tape
2. The finite control and the head of tape that is responsible for reading the current symbol of input. The head of the tape will switch from left to right,
3. A finite set of states through which the system has to go through.
4. Finite set of symbols that are used in the construction of the Turing machine logic, called external symbols.
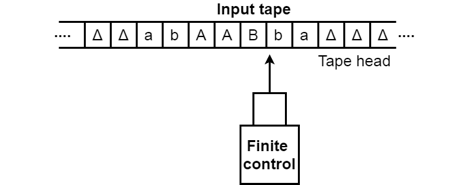
Fig 2: Basic model of TM
Various features of the Turing machine exist:
● It has an external memory that recalls an arbitrary, long input list.
● It has infinite capability for memory.
● The model has a method in which it is easy to read the input on the tape on the left or right.
● Depending on its input, the computer may generate a certain output. It will often be appropriate for the same input to be used to produce the output. So, the distinction between input and output has been abolished in this machine. It is therefore possible to use a standard set of alphabets for the Turing machine.
Key takeaway:
- TM may be a mathematical model that consists of associate infinite length tape divided into cells on which input is given.
- It consists of a head that reads the input tape.
- A state register stores the state of the information processing system.
Even though they are recursively enumerable, the Turing machine embraces all the language. Recursive implies repeating for any number of times the same set of rules, and enumerable means a collection of elements.
Computable attributes, such as addition, multiplication, subtraction, division, power function, and many more are also accepted by the TM.
Example: Creating a Turing machine which accepts the language of aba over ∑ = {a, b}
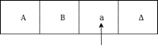
Sol: We'll think that the string 'aba' is positioned like this on the input tape:

The tape head reads the sequence up to the Δ characters. If the tape head is read 'aba' string, then after reading, TM will stop.
Now we're going to see how this turbo machine is going to work for aba. The condition is originally q0 and the head points to an as:

The next move is δ (q0, a) = δ (q1, A, R) which means it goes to state q1, replaced by A and head moves toward right:

The next move is δ (q1, b) = δ (q2, B, R) which means it goes to state q2, replaced by B and head moves toward right:
The next move is δ (q2, a) = δ (q3, A, R) which means it goes to state q3, replaced by A and head moves toward right:

The move δ (q3, Δ) = (q4, Δ, S) therefore, it will go to state q4 which is the HALT state and HALT state is always an accept state for any Turing Machine.
State | a | b | ᇫ |
q0 | (q1, A, R) | - | - |
q1 | - | (q2, B, R) | - |
q2 | (q3, A, R) | - | - |
q3 | - | - | (q4, ᇫ, S) |
q4 | - | - | - |
The Turing machine can be represented by transition diagram -
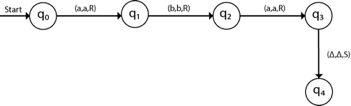
Fig 3: Transition diagram for Turing machine
The Turing machine is a mathematical model of a machine that operates mechanically on a tape. There are symbols on this tape that the machine can read and write one at a time with the help of a tape head. The operation is entirely determined by a finite set of elementary instructions such as "write a 1 in state 42 if the symbol seen is 0; change to state 17 if the symbol seen is 1; write a 1 in state 17 if the symbol seen is 0 and change to state 6;" and so on. Turing imagines a person, whom he calls the "computer," who performs these deterministic mechanical laws slavishly in the original essay ("On Computable Numbers, with an Application to the Entscheidungs problem").
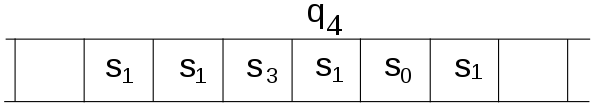
Fig 4: The instruction to be performed (q4) is shown over the scanned square
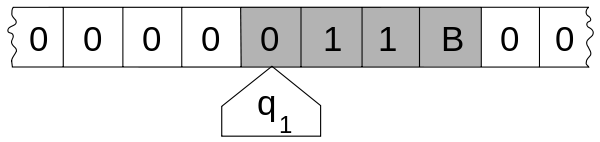
Fig 5: the internal state (q1) is shown inside the head, and the illustration describes the tape as being infinite and pre-filled with "0", the symbol serving as blank.
A Turing machine is made up of the following components:
● A tape with cells that are stacked one on top of the other. A symbol from a finite alphabet is contained in each cell. A specific blank symbol (here spelled as '0') and one or more other symbols make up the alphabet. The tape is supposed to be extensible to the left and right arbitrarily, ensuring that the Turing machine has access to as much tape as it requires for computing. The blank symbol is supposed to be filled in cells that have not been written in before. In some models, the tape has a specific symbol on the left end, and it extends or is infinitely extensible to the right.
● A head that can read and write symbols on the tape as well as move the tape left and right one cell at a time. In certain types, the tape is stationary while the head moves.
● A state register that stores the state of one of a finite number of Turing machines. The special start state with which the state register is initialized is one of them. These states, according to Turing, take the place of the "state of mind" that a person conducting calculations would be in.
● Given the present state(qi) of the machine and the symbol(aj) it is reading on the tape (symbol now under the head), a finite table of instructions directs the machine to do the following in order (for the 5-tuple models):
● Either delete or add a symbol (replacing aj with aj1).
● Move the head (which can take values of 'L' for one step left, 'R' for one step right, or 'N' for staying in the same spot, as indicated by dk).
● Assume the same or a different condition as directed (go to state qi1).
There are some techniques for Turing machine, which are -
● Storage in finite control
Technique: - Using the finite control of a TM to hold a finite amount of data, in addition to the state.
Method: - Assuming the state as [q, A, B, C], for example, when the finite control holds three data elements A, B, and C.
Example:
Design a TM to recognize 01* + 10*. The set of states are of the form [qi, X] where qi = q1, q2; X = 0, 1, B.
• The control portion (state) remembers what the TM is doing (q0 = not read 1st symbol; q1 = reverse).
• The data portion remembers the first symbol seen (0, or 1).
The transition function d is as follows.
• d([q0, B], a) = ([q1, a], a, R) for a = 0, 1. --- Copying the symbol it scanned.
• d([q1, a],a) = ([q1, a],a, R) where a is the complement of a = 0, 1. --- Skipping symbols which are complements of the 1st symbol read (stored in the state as a).
• d([q1, a], B) = ([q1, B], B, R) for a = 0, 1. --- Entering the accepting state [q, B] when reaching the 1st blank.
● Multi tracks
● Assuming the tape of a TM is composed of several tracks.
● For example, if there are three tracks, we use the tape symbol as [X, Y, Z]
Example
The TM recognizes the non-CFL language
L = {wcw | w is in (0 + 1) +}.
Que: Why does not the power of the TM increase in this way?
Answer: just a kind of tape symbol labeling.
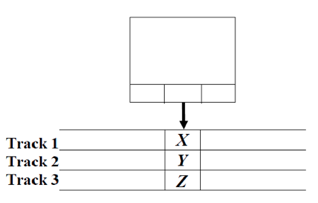
Fig 6: Multi track
● Checking off symbols
We use one tape track to indicate that some symbols have Without modifying them, they are read.
Example: Consider a Turing machine for accepting
w#w#w, w ∈ {a, b}∗
Sol: A tape considered is two tracks.
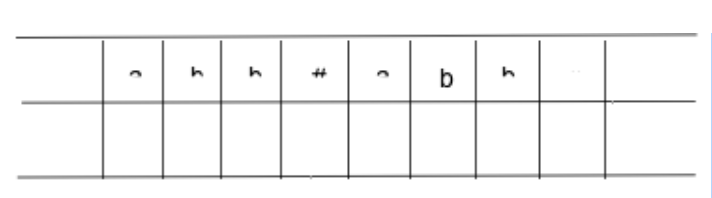
When the TM reads the first a in state q0, it stores it by taking the state as a pair) in its memory, checks off 'a by printing a 'in the second track below a, moves right and checks if the symbol is a' a 'after the # symbol.
If it is marked by putting a √ in the second direction, it moves correctly and
The first symbol checks again after # is a 'a' and it also labels if so. For each unmarked, it then moves left and repeats the process in each block, the leftmost symbols.
The computer stops accepting the string if all the symbols in the first block match the second and third blocks.
The mapping as follow:
δ(q0, [a, 6b]) = ([q, a], [a, √], R)
δ(q0, [b, 6b]) = ([q, b], [b, √], R)
The TM starts reading from the leftmost symbol and marks it, also stored state and checks whether it is ‘a’ or ‘b’.
δ([q, a], [a, 6b]) = ([q, a], [a, 6b], R)
δ([q, a], [b, 6b]) = ([q, a], [b, 6b], R)
δ([q, b], [a, 6b]) = ([q, b], [a, 6b], R)
δ([q, b], [b, 6b]) = ([q, b], [b, 6b], R)
In the first block to the right, the head moves through symbols
δ([q, a], [#, 6b]) = ([p, a], [#, 6b], R)
δ([q, b], [#, 6b]) = ([p, b], [#, b], R)
In the first track, when the head encounters a #, the first state component is changed to p
δ([p, a], [a, √]) = ([p, a], [a, √], R)
δ([p, a], [b, √]) = ([p, a], [b, √], R)
δ([p, b], [a, √]) = ([p, b], [a, √], R)
δ([p, b], [b, √]) = ([p, b], [b, √], R)
δ([p, a], [a, 6b]) = ([r, a], [a, √], R)
δ([p, b], [b, 6b]) = ([r, b], [b, √], R)
When a first unchecked symbol is found, it marks it by placing a √ in the second direction and changing the first component of the state to r.
δ([r, a], [a, 6b]) = ([r, a], [a, 6b], R)
δ([r, b], [a, 6b]) = ([r, b], [a, 6b], R)
δ([r, a], [b, 6b]) = ([r, a], [b, 6b], R)
δ([r, b], [b, 6b]) = ([r, b], [b, 6b], R)
When the first part of the state is r, the head moves through the second block without changing symbols
δ([r, a], [#, 6b]) = ([s, a], [#, 6b], R)
δ([r, b], [#, 6b]) = ([s, b], [#, 6b], R)
It moves straight into the third block when it encounters a # in the first track, changing the first component of the state to s
δ([s, a], [a, √]) = ([s, a], [a, √], R)
δ([s, a], [b, √]) = ([s, a], [b, √], R)
δ([s, b], [a, √]) = ([s, b], [a, √], R)
δ([s, b], [b, √]) = ([s, b], [b, √], R)
This goes right in search of the unchecked symbol
δ([s, b], [b, 6b]) = (t, [b, √],L)
δ([s, a], [a, 6b]) = (t, [a, √],L)
If an unchecked sign is found in the third, it marks it by placing a √ in the second direction and begins heading left.
δ(t, [a, √]) = (t, [a, √],L)
δ(t, [b, √]) = (t, [b, √],L)
δ(t, [#, √]) = (t0, [#, √],L)
In state t ', it passes into the second block
δ(t0, [a, 6b]) = (t0, [a, 6b],L)
δ(t0, [b, 6b]) = (t0, [b, 6b],L)
δ(t0, [a, √]) = (t0, [a, √],L)
δ(t0, [b, √]) = (t0, [b, √],L)
In second block, it moves left
δ(t0, [#, 6b]) = (t00, [#, b],L)
In the first block, moves left in state t”
δ(t00, [a, 6b]) = (t00, [a, 6b],L)
δ(t00, [b, 6b]) = (t00, [b, 6b],L)
In the first block it moves left through an unchecked symbol.
When it faces a checked symbol, it moves right in the state q0 and repeat the whole process.
δ(t00, [a, √]) = (q0, [a, √], R)
δ(t00, [b, √]) = (q0, [b, √], R)
In this manner, the computer scans for the same symbols in the
Lines, first, second and third
● Subroutine
Much as a computer programme has a primary procedure and procedure the TM can also be programmed to have subroutines, A core TM and TMs that function as subroutines.
Suppose we're going to make n copies of a word w Input is #w# and the output is #w# w| ww{z. . . w} n times.
In this situation, we can compose the mappings for a TM Msub that ends with #w#xw when launched on #w#x. This is called Msub x times by the key TM.
Likewise, for Multiplying two unary numbers m and n, on m occasions, n must be copied. For copying we can write a sub TM and main TM will name this m times.
The M1 and M2 states must be disjointed in order for a Turing machine M1 to use another Turing machine M2 as a subroutine. The control also goes to the initial state of M2 when M1 wishes to call M2, from the state of M1. When the subroutine stops and returns to M1, from M2's stopping state, the subroutine returns to M2 the computer goes into a certain M1 mode.
Note that a subroutine Turing Machine calls its subroutine another Turing machine (TM). To construct a Turing machine in a top-down way, separating the job into tasks and writing.
Being a partial function, a TM transition feature means that there are input pairs for which the transition feature is not defined.
δ(non-halting-state, symbol) = UNDEF
By adding a new dedicated "run forever" state, R:, we can easily compensate for such an omission
δ(R,σ) = (R,σ) ∀ σ ∈ Σ
Simply send a missing transition to this state without tape modification with this addition, i.e.,
δ(non-halting-state, symbol) = (R, symbol)
The easiest computer we can create that runs indefinitely is this:
RunForever = ({s,h}, Σ, {}, s, {h} )
There are states of beginning and halt, but no transitions, implying that all transitions go to some state of "run forever"
1. Multiple tracks Alan Turing Machine:
● A k-tack Alan Turing machine(for some k>0) has k-tracks and one R/W head
That reads and writes all of them one by one.
● A k-track information processing system may be simulated by one track information processing system.
2. Two-way infinite Tape Alan Turing Machine:
● Infinite tape of two-way infinite tape information processing system is
Boundless in each direction left and right.
● Two-way infinite tape information processing system may be simulated by
Unidirectional infinite {turing|Turing|Alan Alan Turing|Alan Mathison
Turing|mathematician} machine(standard Turing machine).
3. Multi-tape Alan Turing Machine:
● It has multiple tapes and is controlled by one head.
● The Multi-tape information processing system is completely different from the k-track information processing system however communicative power is the same.
● Multi-tape information processing system may be simulated by a single-tap information processing system.
4. Multi-tape Multi-head Alan Turing Machine:
● The multi-tape information processing system has multiple tapes and multiple Heads.
● Each tape is controlled by a separate head.
● Multi-Tape Multi-head information processing systems may be simulated by normal information processing systems.
5. Multi-dimensional Tape Alan Turing Machine:
● It has multi-dimensional tape wherever the head will move any direction that’s left, right, up or down.
● Multi-dimensional tape information processing system may be simulated by a one-dimensional information processing system.
6. Multi-head Alan Turing Machine:
● A multi-head information processing system contains 2 or additional heads to scan the symbols on constant tape.
● In one step all the heads sense the scanned symbols and move or write severally.
● Multi-head information processing system may be simulated by single head information processing system.
7. Non-deterministic Alan Turing Machine:
● A non-deterministic information processing system encompasses a single, method of infinite tape.
● For a given state and input image has at least one option to move (finite range of decisions for consecutive move), every selection has many decisions of path that it’d follow for a given input string.
● A non-deterministic information processing system is an adored settled information processing system.
Typically, programs are made up of loops that are either limited or infinite in length.
The program's overall output is entirely dependent on the input it receives.
The program may contain numerous different numbers of loops, which can be linear or nested.
The Halting Challenge is the problem of determining whether a given arbitrary computer program will stop operating or run in an infinite loop for the given input dependent on its input.
The Halting Problem states that it is difficult to develop a computer program that can decide if a program should halt for an input in a limited amount of time.
Furthermore, the Halting Problem never claims that determining whether a given random program will halt is impossible (stop).
In general, it asks, "Specify a random program and an input, determine whether the given random program will halt when that input is provided."
Writing Halting Problem
Input: A Turing machine and an input string T.
Problem - Does the Turing machine complete the T-string computation in a finite number of steps? Either yes or no must be the answer.
Sol: We will first assume that there is such a Turing machine to solve this problem, and then we will demonstrate that it contradicts itself. This Turing machine would be called a Halting machine that produces in a finite amount of time a 'yes' or no'. The performance comes as 'yes' if the stopping machine finishes in a finite amount of time, otherwise as no'.
The following is a Halting Computer block diagram -
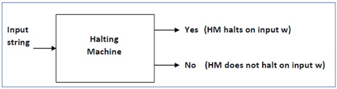
Fig 7: Halting machine
Now we will design an inverted halting machine (HM)’ as -
● If H returns YES, then loop forever.
● If H returns NO, then halt.
Below is the block diagram of inverted halting machine -
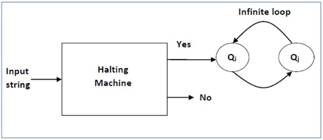
Fig 8: Inverted halting machine
In addition, as follows, a machine (HM)2 whose input itself is constructed -
● If - (HM)2 halts on input, loop forever
● Else - halt
Now, we have a contradiction. So, the halting problem is undecidable.
Now that we've established that there are languages that aren't Turing decidable, the next question is if there are languages that aren't Turing-recognizable. Remember that a language L is Turing recognized if it has a Turing machine that takes exactly the words in L but may either reject or loop forever on non-L input.
We'll prove that ATM, the complement of ATM, isn't Turning-compliant. The proof comes in the form of a contradiction. Assume the ATM is Turing-compatible with some Turing machine M2. Recall that the ATM is Turing-compatible with some Turing machine M1. We show that by running M1 and M2 in parallel, we may decide on an ATM.
Consider alternate running M1 and M2 on some input w, one step at a time, and returning the result when either one accepts. We assert that this process will come to a halt in either instance of w ATM or w / ATM:
- If w is in an ATM, M1 accepts w for some value k after k steps, and the total process comes to a halt after 2k steps.
- If w is in an ATM, M2 accepts w for some value k after k steps, and the total operation halts after 2k steps.
A theorem that states that a language A is decidable if and only if it is Turing- and co-Turing-recognizable.
A reduction is a method of transforming one problem into another so that the answer to the second problem can be applied to the first. The first problem is said to be reducible to the second problem.
● Informal Examples: Measuring the area of a rectangle reduces to measuring the length of the sides; inverting a matrix reduces to solving a system of linear equations.
● The problem Ld reduces to the problem Atm as follows: “To see if w ∈ Ld check if hw, wi ∈ Atm.”
If there is a function f that converts strings in A to strings in B, then language A (represented as AB) is reducible to language B (represented as AB).
w ɛ A <=> f(w) ɛ B
Theorem 1: If A ≤ B and B are both decidable, then A is as well.
Theorem 2: If A ≤ B and A are both undecidable, then B is as well.
A Turing reduction from a decision issue AA to a decision problem BB is an oracle machine that decides problem AA given an oracle for BB in computability theory (Rogers 1967, Soare 1987). It can be thought of as an algorithm that might be used to solve AA if a subroutine for solving B was available. The technique can be used to function problems in a similar way.
If there is a Turing reduction from A to B, then any algorithm for B[a] can be used to generate an algorithm for A by inserting the algorithm for B at each point where the oracle machine computing A queries the oracle for B. However, because the oracle machine may query the oracle several times, the resulting algorithm may asymptotically take longer than either the method for B or the oracle machine computing A. A Cook reduction is a Turing reduction in which the oracle machine runs in polynomial time.
Alan Turing gave the first formal definition of relative computability, then known as relative reducibility, in terms of oracle machines in 1939. Stephen Kleene later established an equivalent concept in terms of recursive functions in 1943 and 1952. Emil Post coined the word "Turing reducibility" to describe the concept in 1944.
Use of Reducibility
Because every reduction from a set B to a set A has only a finite number of steps to establish if a single element is in A, it can only do a finite number of membership inquiries in the set B. The usage function makes it precise when the quantity of information about the set B utilized to compute a single bit of A is discussed. The function that sends each natural number n to the largest natural number m whose membership in the set B was questioned by the reduction while finding the membership of n in A is known as the use of a reduction.
Recursion Theorem
Some Turing Machines can recreate their own descriptions, according to the recursion theorem.
It is implied that we can create an equivalent TM with this characteristic from any TM.
Our ultimate goal is to create a Turing machine that prints and runs its own source code. We demonstrated the existence of SELF, a Turing machine that ignores its input while printing its source code. The recursion theorem is proved in a similar way.
Lemma: There exists a computable function q: Σ∗ → Σ ∗ such that q(w) = hPwi, where Pw is a Turing machine that prints w and hats.
Theorem (Recursion theorem): Let T be a Turing machine that computes a function t: Σ∗ × Σ ∗ → Σ ∗. There exists a Turing machine R that computes a function r: Σ∗ → Σ ∗, where for every w,
r(w) = t (hRi, w).
According to the theorem, there exists a Turing machine R that computes t on hRi and some input for any arbitrary computable function t.
Proof: We build a Turing Machine R out of three parts: A, B, and T, where T is the theorem's statement.
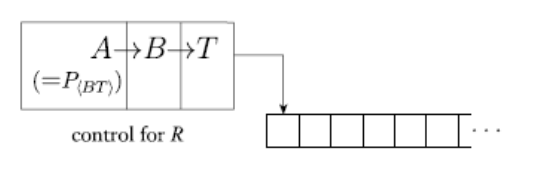
Fig 9: Schematic of R
Let w represent the original R input. The Turing machine (BT)#w is represented as A, where # is a special character used to separate the original input. Because of the lemma, A now exists. The tape includes (BT) #w after A has completed its run.
Following that, B is a Turing machine that generates the string q(x) from the input x, where q is the lemma. It then prints (q(x), x), and then stops. When B follows A, the string (P(BT#w)) = (A) is created. It is printed
((A), (BT)#w) = (ABT #w) = (R#w)
Finally, T runs on its input, which is (R#w) here. This completes the proof.
A multi-track non-deterministic Turing machine with a tape of some limited finite length is a linear bounded automaton.
Length = function (Length of the initial input string, constant c)
Here,
Memory information ≤ c × Input information
The measurement is limited to the region bounded by constants. There are two special symbols in the input alphabet that act as left end markers and right end markers, indicating that the transitions do not switch either to the left of the left end marker or to the right of the tape's right end marker.
A linear bounded automata can be defined in 8-tuple -
(Q, X, ∑, q0, ML, MR, δ, F)
Where
● Q is a finite set of states
● X is the tape alphabet
● ∑ is the input alphabet
● q0 is the initial state
● ML is the left end marker
● MR is the right end marker where MR ≠ ML
● δ is a transition function which maps each pair (state) to (state, tape symbol, Constant ‘c’) where c could become 0 or +1 or -1.
● F is the set of final states.
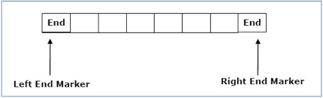
Fig 10: Linear bounded automata
Key takeaway
- The measurement is limited to the region bounded by constants.
- A linear bounded automaton is a multi-track non-deterministic Turing machine with a tape of some limited finite length.
References:
- John E. Hopcroft, Rajeev Motwani, Jeffrey D.Ullman, “Introduction to Automata Theory Languages Sanjeev Arora and Boaz Barak, “Computational Complexity: A Modern Approach”,
- Cambridge University Press, ISBN: 0521424267 97805214242643
- John Martin, “Introduction to Languages and The Theory of Computation”, 2nd Edition, McGrawHill Education, ISBN-13: 978-1-25-900558-9, ISBN-10: 1-25-900558-5
- J.Carroll & D Long, “Theory of Finite Automata”, Prentice Hall, ISBN 0-13-913708-45 and Computation”, Addison-Wesley,ISBN
- Daniel Cohen, “Introduction to Computer Theory”, Wiley & Sons, ISBN 97881265133454