Unit 1
Vector Algebra
The various mathematical operations such as addition, subtraction, multiplication etc can be performed with the vectors.
1.1.1 Addition of vectors:
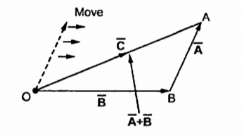
Consider two coplanar vectors as shown in figure. The vectors which lie in the same plane are called coplanar vectors.
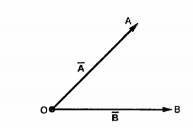
Let us find the sum of these two vectors 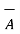 and
and  shown in figure. The procedure is to move one of the two vectors parallel to itself at the tip of the other vector. Thus, move
shown in figure. The procedure is to move one of the two vectors parallel to itself at the tip of the other vector. Thus, move  parallel to itself at the tip of
parallel to itself at the tip of 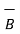 . Then join the tip of
. Then join the tip of 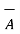 moved to the origin . This vector represents resultant which is the addition of the two vectors
moved to the origin . This vector represents resultant which is the addition of the two vectors 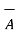 and
and  . This is shown in figure . The resultant
. This is shown in figure . The resultant  then is
then is 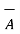 and
and 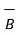
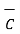 =
=  +
+ 
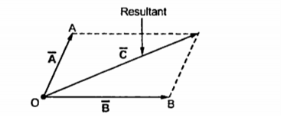
Another method of performing the addition of vectors is the parallelogram rule. Complete the parallelogram as shown in figure. Then the diagonal of the parallelogram represents the addition of two vectors.
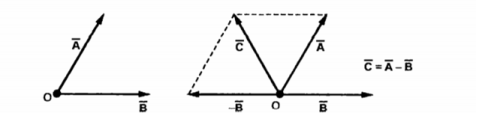
1.1.2 Subtraction of Vectors
The subtraction of vectors can be obtained from the rules of addition. If 
Is to be subtracted from 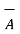 then based on addition it can be represented as ,
then based on addition it can be represented as ,
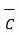 =
=  + (-
+ (- 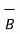 )
)
Thus, reverse the sign of  that is reverse its direction by multiplying it with -1and then add it to
that is reverse its direction by multiplying it with -1and then add it to  to obtain the subtraction. This is shown in the figure
to obtain the subtraction. This is shown in the figure
If 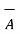 = 3 ax + 2 ay + 6 az and
= 3 ax + 2 ay + 6 az and  2 ax + 5 ay – 3az . Find
2 ax + 5 ay – 3az . Find
i) 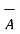 +
+ 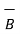
Ii) 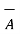 -
- 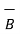
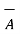 +
+ 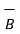 = 3
= 3 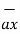 + 2
+ 2 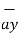 + 6
+ 6 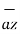 + 2
+ 2 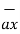 + 5
+ 5 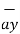 – 3
– 3 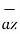 = 5
= 5 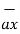 + 7
+ 7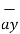 + 3
+ 3 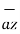
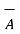 -
- 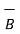 = 3
= 3 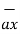 + 2
+ 2  + 6
+ 6 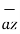 -( 2
-( 2 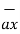 + 5
+ 5 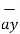 – 3
– 3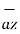 )
)
= 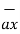 – 3
– 3  + 9
+ 9 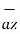
1.1.3 Components of vectors
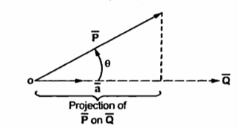
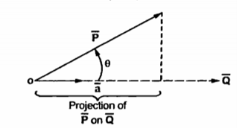
To find the component of the vector in a given direction
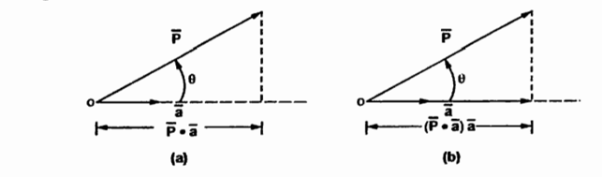
Consider a vector 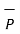 and the unit vector
and the unit vector 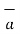 as shown in figure . The component of vector in
as shown in figure . The component of vector in 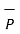 in the direction of unit vector
in the direction of unit vector 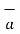 is
is  .
. 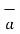 . This is the scalar quantity shown in figure (a)
. This is the scalar quantity shown in figure (a)
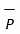 .
. 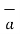 = |
= | | |
| |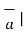 cos Ɵ = |
cos Ɵ = |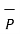 | cos Ɵ.
| cos Ɵ.
The sign of the component is positive if 0≤Ɵ≤ 90 o while the sign of this component is negative if 90 o <Ɵ≤ 180 o .
If the component vector of  is in the direction of unit vector
is in the direction of unit vector 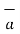 is required then multiply the component obtained by that unit vector as shown in fig(b). Thus
is required then multiply the component obtained by that unit vector as shown in fig(b). Thus
(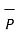 .
. 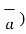
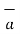 is the component vector of
is the component vector of 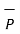 in the direction of
in the direction of 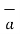 .
.
The component of 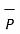 in the direction of
in the direction of 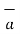 x is
x is  .
. 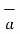 x that is Px while the component vector of
x that is Px while the component vector of  in the direction of
in the direction of  x is
x is 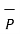 .
.  x
x
If the projection of 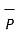 on the other vector
on the other vector 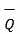 is obtained then it is necessary to find unit vector in the direction of
is obtained then it is necessary to find unit vector in the direction of 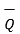 first that is
first that is 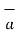 Q . Then the projection of
Q . Then the projection of 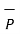 on
on 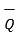 is given
is given 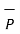 .
. 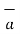 Q .
Q .
As 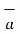 Q =
Q = 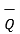 / |
/ |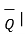 then the projection of
then the projection of  on
on 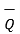 can be expressed as
can be expressed as
 .
. 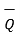 / |
/ | =
= 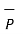 .
. 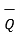 / |
/ |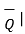
1.1.4 Scalar
If we multiply a vector ⃑A by a scalar k, we obtain a vector ⃑B such that
⃑B = 𝑘 ⃑A⃑
The magnitude of ⃑B is simply equal to |𝑘| times the magnitude of ⃑A .
If k < 0 then ⃑B in the opposite direction from ⃑A
If k > 0 then ⃑B in the same direction as ⃑A
So, vector ⃑B is said to be a dependent vector.
1.1.5 Vector Multiplication
There are two types of vector multiplication:
- Dot product(or) Scalar product
- Cross Product (or) Vector Product
Dot Product :
The scalar or dot of the two vectors  and
and  is denoted as
is denoted as  .
. 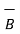 and defined as the product of the magnitude of A , the magnitude of B and the cosine of the smaller angle between them.
and defined as the product of the magnitude of A , the magnitude of B and the cosine of the smaller angle between them.
It also can defined as the product of magnitude of 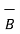 and the projection of
and the projection of 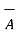 onto
onto 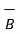 or vice versa.
or vice versa.
Mathematically it is expressed as,
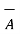 .
. 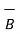 = |
= |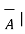 |
|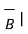 cos Ɵ AB --------------------------------------(1)
cos Ɵ AB --------------------------------------(1)
The result of such a dot product is scalar and hence called scalar product.
Properties of Dot Product
The various properties of the dot product are :
- If two vectors are parallel to each other Ɵ = 0 0 then cos Ɵ AB =1 thus
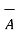 .
. 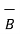 = |
= | |
|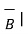 for parallel vectors -------------------------------------(2)
for parallel vectors -------------------------------------(2)
2. If the two vectors are perpendicular to each other Ɵ = 90 o then cos Ɵ AB =0 thus
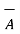 .
. 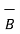 = 0 for perpendicular vectors ------------------------------(3)
= 0 for perpendicular vectors ------------------------------(3)
If the dot product of the two vectors is zero then the two vectors are perpendicular to each other.
The dot product obeys commutative law
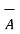 .
. 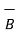 =
= 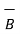 .
. 
3. The dot product obeys distributive law,
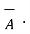 (
( 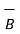 +
+ 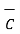 ) =
) = 
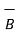 +
+ 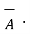

4. If the dot product of vector with itself is performed the result is the square of the magnitude of that vector.
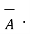
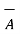 = |
= |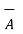 | |
| |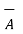 | cos 0 o = |
| cos 0 o = |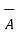 | 2
| 2
5. Consider the unit vectors  ,
, 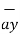 ,
, 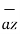 in cartesian co-ordinate system. All these vectors are mutually perpendicular to each other. Hence the dot product of different unit vectors is zero.
in cartesian co-ordinate system. All these vectors are mutually perpendicular to each other. Hence the dot product of different unit vectors is zero.
 .
.  =
=  .
.  =
= 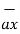 .
. 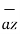 =
= 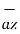 .
. 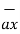 =
= 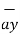 .
.  =
= 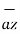 .
. 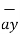 =0
=0
Any unit vector dotted with itself is unity
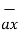 .
. 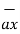 =
= 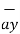 .
.  =
=  .
.  = 1
= 1
Applications of Dot Product :
The applications of dot product are :
1.To determine the angle between the two vectors .
The angle can be determined by
Ɵ = cos -1 { 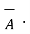
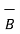 )/ |
)/ |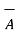 | |
| |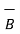 |}
|}
2. Physically work done by a constant force can be expressed as dot product of two vectors.
Consider a constant force 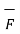 acting on a body and it causes the displacement
acting on a body and it causes the displacement 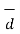 of that body. Then the work done W is the product of the force and the component of the displacement in the direction of force which can be expressed as ,
of that body. Then the work done W is the product of the force and the component of the displacement in the direction of force which can be expressed as ,
W = | d cos Ɵ =
d cos Ɵ = 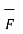 .
. 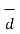 of that body. Then the work done W of the force and the component of the displacement in the direction of force which can be expressed as ,
of that body. Then the work done W of the force and the component of the displacement in the direction of force which can be expressed as ,
W = | d cos Ɵ =
d cos Ɵ = 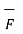 .
. 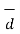
But if the force applied varies along the path then the total work done is to be calculated by the integration of a dot product as ,
W =  .
. 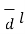
Problem:
Given the two vectors ,
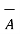 = 2
= 2 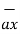 - 5
- 5 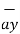 - 4
- 4 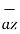 and
and 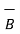 = 3
= 3 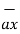 + 5
+ 5  + 2
+ 2 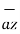 . Find the dot product and the angle between the two vectors .
. Find the dot product and the angle between the two vectors .
The dot product is ,
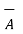 .
. 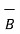 = Ax Bx + Ay By + Az Bz = (2x3) +(-5)(5) + (-4)(2) = -27
= Ax Bx + Ay By + Az Bz = (2x3) +(-5)(5) + (-4)(2) = -27
As 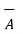 .
. 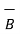 is negative it is expected that the angle between the two is greater than 90 o .
is negative it is expected that the angle between the two is greater than 90 o .
|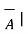 =
=  (2) 2 + (-5) 2 + (-4) 2 =
(2) 2 + (-5) 2 + (-4) 2 = 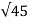
|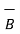 | =
| =  (3) 2 + (5) 2 + (2) 2 =
(3) 2 + (5) 2 + (2) 2 = 
Ɵ= cos -1 { 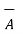 .
. 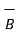 / |
/ |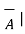 |
|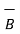 | } = cos -1 { -27 /
| } = cos -1 { -27 / 
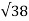 } = 130.762 o
} = 130.762 o
Given vector field 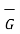 = (y-1)
= (y-1) 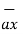 + 2x
+ 2x 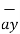 . Find this vector field at P(2,3,1) and its projection on
. Find this vector field at P(2,3,1) and its projection on 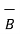 = 5
= 5
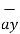 + 2
+ 2 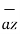 .
.
The field  at point P is
at point P is
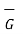 at P = 2
at P = 2 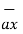
 substituting co-ordinates of P in
substituting co-ordinates of P in 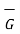
To find its projection on  first find
first find 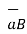 the unit vector in the direction of
the unit vector in the direction of 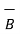
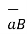 =
= 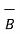 / |
/ | 5
5
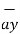 + 2
+ 2 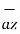 /
/ 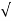 (5) 2 +(-1) 2 +(2) 2 = 0.9218
(5) 2 +(-1) 2 +(2) 2 = 0.9218  – 0.1825
– 0.1825 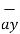 + 0.3651
+ 0.3651 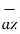
Hence projection of  at P on the vector
at P on the vector 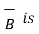
(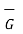 at P) .
at P) . 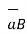 = (2x 0.9218)+(4x-0.1825)+(0x0.3651) = 1.0956.
= (2x 0.9218)+(4x-0.1825)+(0x0.3651) = 1.0956.
Cross Product :
Consider the two vectors 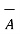 and
and  then the cross product is denoted as
then the cross product is denoted as  x
x 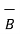 and defined as the product of the magnitudes
and defined as the product of the magnitudes 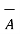 and
and 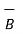 and the sine of the smaller angle between
and the sine of the smaller angle between 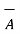 and
and 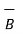 . But this product is a vector quantity and has a direction perpendicular to the plane containing the two vectors
. But this product is a vector quantity and has a direction perpendicular to the plane containing the two vectors  and
and 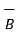
But for any plane there are two perpendicular directions upwards and downwards .
Mathematically
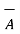 x
x 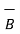 = |
= | ||
||  | sin Ɵ AB
| sin Ɵ AB 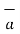 N where
N where 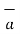 N = unit vector perpendicular to the plane of
N = unit vector perpendicular to the plane of 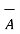 and
and 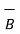 in the direction decided by the right hand screw rule.
in the direction decided by the right hand screw rule.
Properties of cross product are ,
- The commutative law is not applicable to the cross product. Thus
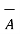 x
x  ≠
≠ 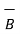 x
x 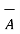
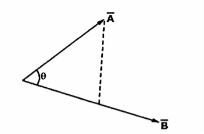
Consider two vectors shown in fig(a) . Then  x
x  gives unit vector
gives unit vector  N in the upward direction. But if
N in the upward direction. But if 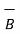 x
x 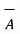 is obtained then direction of
is obtained then direction of 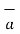 N must be determined by rotating
N must be determined by rotating  into
into 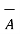 which results in down ward direction. This shown in fig(b) . Hence cross product is not commutative.
which results in down ward direction. This shown in fig(b) . Hence cross product is not commutative.
2. Reversing the order of the vectors  and
and 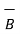 a unit vector
a unit vector 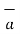 N reverses its direction. Hence we can write ,
N reverses its direction. Hence we can write ,
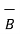 x
x  = -[
= -[ 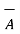 x
x 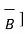
It is anticommutative in nature.
If order of cross product is changed , the magnitude remains the same but the direction is reversed.
3. The cross product is not associative.
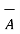 x
x 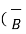 x
x 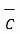 ) ≠ (
) ≠ (  x
x 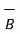 ) x
) x 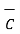
4. If the two vectors are parallel to each other that is they are in the same direction then Ɵ = 0 o and hence cross product of such two vectors is zero.
Thus if cross product of the two vectors is zero then those two vetors are parallel meaning same direction assuming none of the two vectors itself is zero.
5. If the cross product of vector 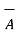 with itself is calculated it is zero as Ɵ = 0 o
with itself is calculated it is zero as Ɵ = 0 o
There fore 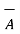 x
x 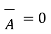
Applications:
The different applications of cross product are:
- The cross product is the replacement to the right -hand rule to determine the direction of force experienced by current carrying conductor placed in a magnetic field. Thus, if I is the current flowing through conductor while
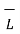 is the vector length considered to indicate the direction of current through the conductor. The uniform magnetic flux density is denoted by
is the vector length considered to indicate the direction of current through the conductor. The uniform magnetic flux density is denoted by 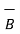 . Then the force experienced by conductor is given by
. Then the force experienced by conductor is given by
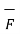 = I
= I 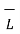 x
x 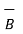
2. Another physical quantity which can be represented by cross product is the moment of force. The moment of force acting on the rigid body which can rotate about an axis perpendicular to a plane containing the force is defined to be the magnitude of the force multiplied by the perpendicular distance from the force to the axis is shown in figure.
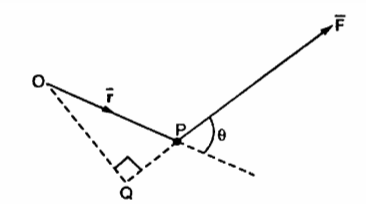
The moment of force 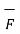 about a point O is
about a point O is 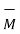 . Its magnitude is |
. Its magnitude is |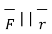 | sin Ɵ is the perpendicular distance of
| sin Ɵ is the perpendicular distance of 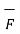 from O meaning OQ.
from O meaning OQ.
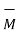 =
= 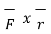 =
=  ||
||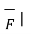 sin Ɵ
sin Ɵ  is the unit vector indicating direction of
is the unit vector indicating direction of 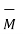 perpendicular to the plane.
perpendicular to the plane.
Problem :
Given the two coplanar vectors
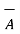 = 3
= 3 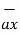 + 4
+ 4  -5
-5 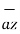 and
and  = -6
= -6 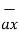 + 2
+ 2 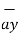 + 4
+ 4 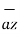 . Obtain the unit vector normal to the plane containing vectors
. Obtain the unit vector normal to the plane containing vectors 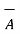 and
and 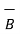

1.1.6 Triple Product
Let 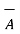 ,
, 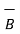 ,
, 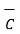 be three given vectors. The product of these three vectors is classified in two ways called
be three given vectors. The product of these three vectors is classified in two ways called
- Scalar triple product 2. Vector triple product.
Scalar triple product :
The scalar triple product of three vectors 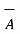 ,
, 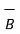 and
and 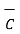 is defined as
is defined as
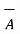 x (
x ( 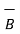 x
x 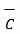 ) =
) = 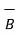 . (
. ( 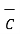 x
x 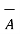 ) =
) = 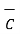 . (
. ( 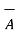 x
x 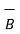 )
)
Thus if,
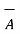 = Ax
= Ax 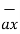 + Ay
+ Ay 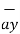 + Az
+ Az 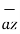
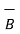 = Bx
= Bx 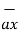 + By
+ By 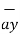 + Bz
+ Bz 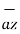
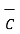 = Cx
= Cx 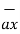 + Cy
+ Cy 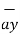 + Cz
+ Cz 
Then the scalar triple product is obtained by the determinant ,
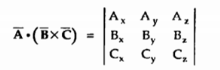
The result of this product is scalar hence the product is called scalar triple product.
Vector triple product
The vector triple product of the three vectors 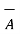 ,
,  ,
, 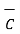 is mathematically defined as
is mathematically defined as
 x(
x( 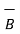 x
x  ) =
) = 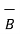 (
( 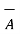 .
.  ) -
) - 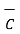 (
( 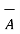 .
. 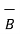 )
)
Characteristics of vector triple product :
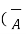 .
. 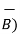
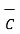 ≠
≠  (
( 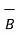 .
. 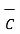 )
)
But  .
. 
 =
= 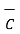 (
(  .
. 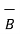 )
)
This is because 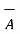 .
.  is a scalar and multiplication by scalar to a vector is commutative.
is a scalar and multiplication by scalar to a vector is commutative.
From the basic definition we can write,
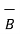 x(
x( 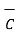 x
x 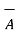 ) =
) =  (
(  .
. 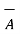 ) -
) - 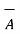 (
( 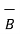 .
. 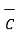 )
)
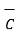 x(
x(  x
x 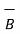 ) =
) =  (
( 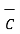 .
. 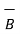 ) -
) - 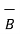 (
( 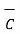 .
. 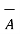 )
)
But the dot matrix is commutative hence  .
. 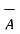 =
= 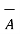 .
. 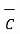 and so on. Hence,
and so on. Hence,
 x(
x( 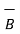 x
x  ) +
) + 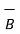 x(
x( 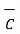 x
x 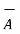 ) +
) + 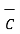 x(
x( 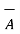 x
x 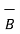 ) =0
) =0
The result of the vector triple product is a vector.
1.1.7 Three orthogonal coordinate systems
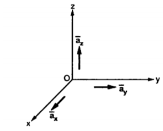
Rectangular:
This system has three co-ordinate axes represented as x,y and z which are mutually at right angles to each other. These three axes intersect at common point called origin of the system. There are two types of such called
- Right- handed system 2. Left- handed system
The right- handed system means if x axis is rotated towards y axis through a smaller angle then this rotation causes upward movement of right- handed screw in the z-axis direction. This is shown in fig(a).
In this system if right hand is used then thumb indicates x-axis, forefinger indicates y-axis and middle finger indicates z-axis. When three fingers are held mutually perpendicular to each other.
In left-handed system x and y axes are interchanged compared to right-handed system. This means the rotation of x-axis through smaller angle causes the downward movement of right-handed screw in the z axis direction as shown in fig(b).

Representing a point in Rectangular Co-ordinate system
A point in rectangular co-ordinate system is located by three co-ordinates namely x,y and z co-ordinates. The point can be reached by moving from origin the distance of x in x-direction , distance of y in y-direction and finally distance of z in z direction.
Consider a point P having co-ordinates x1,y1 and z1 which can be positive or negative.
The point Q(3,-1,2) can be shown as
Base vector :
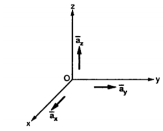
The base vector are the unit vectors that are oriented along the directions of the co-ordinate axes of the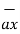 given co-ordinate system. Thus for cartesian co-ordinate system the three base vectors are unit vectors oriented in x,y and z axis of the system. Therefore
given co-ordinate system. Thus for cartesian co-ordinate system the three base vectors are unit vectors oriented in x,y and z axis of the system. Therefore 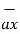 ,
, 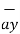 and
and 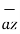 are the base vectors of the cartesian co-ordinate system.
are the base vectors of the cartesian co-ordinate system.
Any point of the x-axis having (x1,0,0) can be represented by a vector joining origin to this point to this point and denoted as x1  .
.
Position and Distance vectors :
Consider a point P(x1,y1,z1) in cartesian co-ordinate system as shown in figure. Then the position vector of point P from the origin directed from origin to point P. This is called radius vector as shown in figure.
The three components of position vector oriented along the three co-ordinate axes with magnitudes x1,y1and z1. Thus the position vector of point P can be represented as
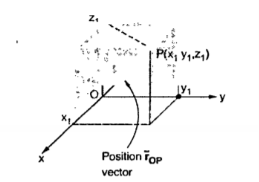
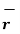 OP = x1
OP = x1 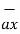 + y1
+ y1 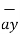 + z1
+ z1 
The magnitude of this vector in terms of three mutually perpendicular components is given by
| OP |=
OP |=  2 + (y1) 2 + (z1) 2
2 + (y1) 2 + (z1) 2
Thus, if point P has co-ordinates (1,2,3) then its position vector is
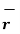 OP =1
OP =1 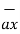 + 2
+ 2  + 3
+ 3 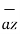
And
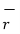 OP =
OP = 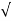 (1) 2 + (2) 2 + (3) 2 =
(1) 2 + (2) 2 + (3) 2 = 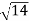 = 3.7416
= 3.7416
Consider two points in a cartesian coordinate system P and Q with the co-ordinates (x1,y1,z1) and (x2,y2,z2) respectively. The individual position vector of the points are
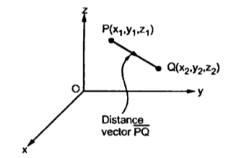

Then the displacement from P to Q is represented by the distance vector 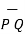 and is given by
and is given by

This is called separation vector.
The magnitude of the vector is given by
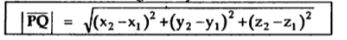
This is called as distance formula.
The unit vector along the direction PQ is given by

Obtain the unit vector in the direction from the origin towards the point P(3,-3,-2)
Solution:
The origin O(0,0,0) while P(3,-3,-2) hence the distance vector 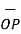 is
is
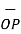 = (3-0)
= (3-0) 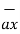 + (-3-0)
+ (-3-0) 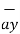 +(-2-0)
+(-2-0) 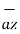 = 3
= 3 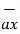 -3
-3  -2
-2 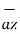
 =
= 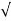 (3) 2 + (-3) 2 + (-2) 2 = 4.6904
(3) 2 + (-3) 2 + (-2) 2 = 4.6904
Hence the unit vector along the direction OP is
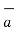 OP =
OP = 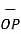 / |
/ |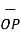 | = 3
| = 3 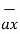 -3
-3  -2
-2 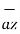 / 4.6904 =
/ 4.6904 =
= 0.6396 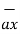 -0.63963
-0.63963 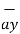 -0.4264
-0.4264 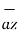
Differential Elements in Cartesian Co-ordinate System
Consider a point P(x,y,z) in the rectangular co-ordinate system . If we increase each co-ordinate by a differential amount a new point P’ will be obtained having co-ordinates (x+dx, y +dy , z+dz)
Dx = differential length in x-direction
Dy = differential length in y-direction
Dz = differential length in z-direction
Hence differential vector length called elementary vector length
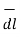 = dx
= dx 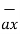 - dy
- dy 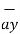 - dz
- dz 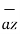 .
.
P is the intersection of the three planes and P’ is the intersection of the new three planes which are displaced from original three planes. These six planes together define a differential volume which is a rectangular parallelepiped as shown in the figure.
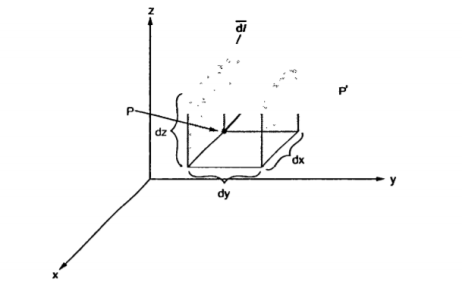
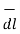 = dx
= dx 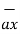 - dy
- dy 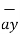 - dz
- dz 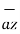 .
.
Hence the differential volume of the rectangular parallelepiped is given by
Dv = dx dy dz
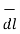 is vector and dv is scalar.
is vector and dv is scalar.
The differential surface area is given by
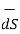 =
= 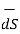
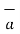 n
n
Ds = Different surfaces area of the element.
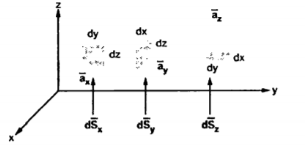
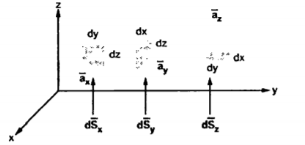
d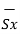 = Differential vector surface area normal to x direction dy dz
= Differential vector surface area normal to x direction dy dz 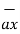
d = = Differential vector surface area normal to y direction dx dz
= = Differential vector surface area normal to y direction dx dz 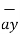
d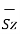 = = Differential vector surface area normal to y direction dx dy
= = Differential vector surface area normal to y direction dx dy 
Given the three points in cartesian co-ordinate system as A(3,-2,1) B (-3,-3,5) , C (2,6,-4)
Find
i) The vector from A to C
Ii) The unit vector from B to A
Iii) The distance from B to C
Iv) The vector from A to the mid-point of the straight line joining B to C.
The position vectors for the given points are :
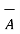 = 3
= 3 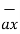 - 2
- 2 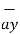 +
+ 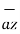 .
.
 = -3
= -3 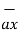 - 3
- 3 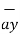 + 5
+ 5 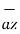 .
.
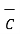 = 2
= 2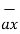 +6
+6  -4
-4 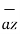 .
.
i) The vector from A to C is
 =
=  -
- 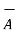 = [ 2-3]
= [ 2-3] 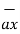 +[6 –(-2)]
+[6 –(-2)] 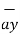 +[-4-1]
+[-4-1] 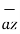 .
.
= -  + 8
+ 8 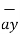 -5
-5 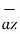 .
.
Ii) For unit vector from B to A obtain the distance vector  first
first
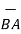 =
= 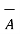 -
- 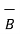
= [ 3 – (-3)] + [ (-2) –(-3) ]
+ [ (-2) –(-3) ]  + [ -4-1]
+ [ -4-1] 
= 6 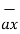 +
+ 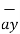 -4
-4 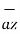 .
.
|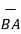 | =
| = 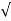 (6) 2 + (1) 2 + (-4)2 = 7.2801.
(6) 2 + (1) 2 + (-4)2 = 7.2801.
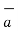 BA =
BA = 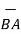 / |
/ | | = 6
| = 6 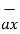 +
+ 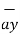 -4
-4 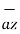 ./ 7.2801
./ 7.2801
Iii) For distance between B and C
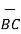 =
= 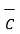 -
- 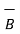 = [ 2 –(-3 ]
= [ 2 –(-3 ] 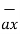 + [6-(-3)]
+ [6-(-3)] 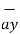 +[-4) –(-5)]
+[-4) –(-5)]  = 5
= 5 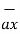 + 9
+ 9 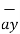 – 9
– 9 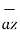
Distance BC =  2 + (9) 2 + (-9) 2 = 13.6747
2 + (9) 2 + (-9) 2 = 13.6747
Iv) Let B(x1,y1,z1 ) and C(x2,y2,z2) then the co-ordinates of the mid-point BC are (x1+x2/2 , y1+y2/2 , z1+z2/2)
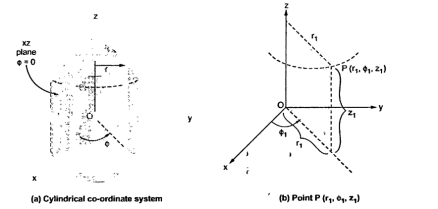
Cylindrical co-ordinate system
The circular cylindrical co-ordinate system is a three-dimensional version of polar co-ordinate system. The surfaces used to define the cylindrical co-ordinate system are :
- Plane of constant z which is parallel to xy plane.
- A cylinder of radius r with z-axis of the cylinder
- A half plane perpendicular to xy plane at angle Ø with respect to xz plane . The angle Ø is called the azimuth angle.
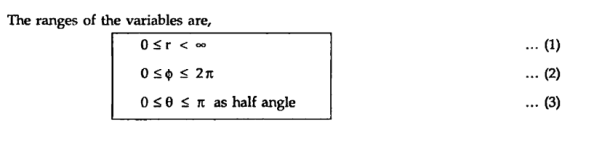
The ranges of the variable are :
0 ≤ r ≤ ∞------------------(1)
0 ≤Ø≤ 2π------------------------------(2)
-∞≤z≤∞--------------------------------------------------(3)
The point P in cylindrical co-ordinate system has three co-ordinates r, Ø and z whose values lie in the ranges given by equations 1,2,3.
The point P(r,Ø1,z1) can be shown in figure (b)
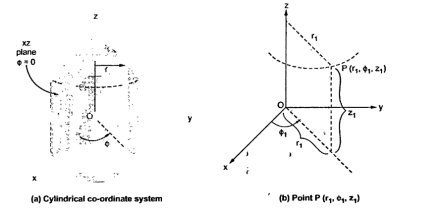
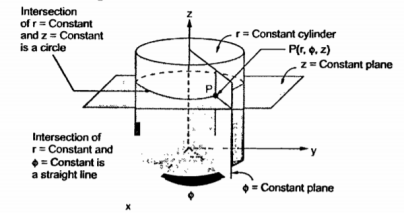
The point P can be defined as the intersection of three surfaces in cylindrical co-ordinate system. These three surfaces are,
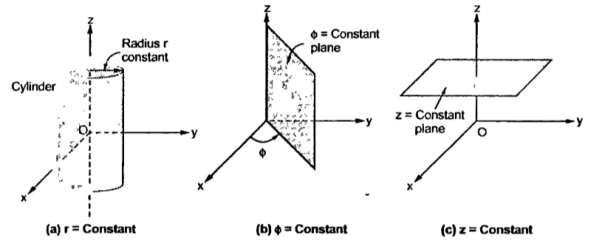
r = Constant which is circular cylinder with z axis as its axis
Ø= Constant plane which is a vertical plane perpendicular to xy plane making angle Ø with respect to xz plane.
z= Constant plane is a plane parallel to xy plane.
These surfaces are shown in figure.
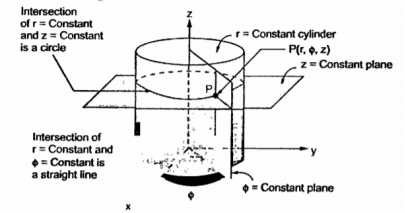
The intersction of any two surfaces out of the above three surfaces is either a line or a circle and intersection of three surfaces define a point.
The intersection of z=constant and r=constant is a circle. The intersection of ɸ=constant and r=constant is a line. The point P which is intersection of all three surfaces is shown in the figure.
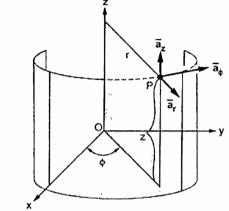
Base vectors:
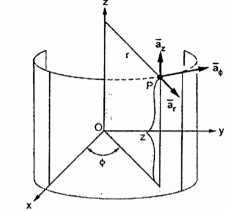
These are mutually perpendicular to each other. The 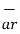 lies in a plane parallel to xy plane and perpendicular to the surface of the cylinder at a given point coming radially outwards. The vector
lies in a plane parallel to xy plane and perpendicular to the surface of the cylinder at a given point coming radially outwards. The vector 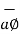 lies also in a plane parallel to xy plane but it is tangent to the cylinder and pointing in the direction of increasing
lies also in a plane parallel to xy plane but it is tangent to the cylinder and pointing in the direction of increasing 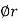 at the given point.
at the given point.
The unit vector 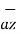 is parallel to z-axis and directed towards increasing z . Hence, vector of point P can be represented as
is parallel to z-axis and directed towards increasing z . Hence, vector of point P can be represented as
 = P r
= P r 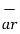 + P ɸ
+ P ɸ 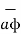 + P z
+ P z 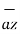
Differential Elements in Cylindrical co-ordinate system
Consider o point P(r,ɸ,z) in a cylindrical co-ordinate system. Let each co-ordinate be increased by differential amount. The differential increments in r,ɸ,z are dr,dɸ and dz respectively.
There are two cylinders of radius r and r+dr. There are two radial planes at the angles ɸ and ɸ+dɸ. And there are two horizontal planes at the heights z+dz. All these surfaces enclose a small volume as shown in figure.
The different lengths in r and z are dz and dr respectively. In ɸ direction dɸ is the change in angle ɸ and is not the differential length. Due to this change dɸ there exists a differential arc length in ɸ direction. This differential length due to dɸ in ɸ direction is r dɸ as shown in figure.
Thus the differential lengths are :
Dr = Differential length in r direction.
r dɸ = Differential length in ɸ direction
Dz = Differential length in z direction
Hence the differential vector length in cylindrical co-ordinate system is given by
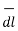 = dr
= dr 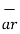 + r dɸ
+ r dɸ 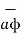 + dz
+ dz 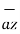
The magnitude of the differential length vector is given y
|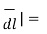
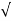 (dr) 2 +( r d ɸ) 2 + (dz) 2
(dr) 2 +( r d ɸ) 2 + (dz) 2
Hence the differential volume of the differential element is given by
Dv = r dr dɸ dz
Spherical co-ordinate system:
The surfaces which are used to define the spherical co-ordinate system on the three cartesian axes are:
- Sphere of radius r, origin as the centre of the sphere.
- A right circular cone with its apex at the origin and its axis as z-axis. It half angle is Ѳ varies from 0 to 180.
- A half plane perpendicular to xy plane containing z axis making an angle Ø with xz plane.
Thus the three co-ordinates of a point P in the spherical co-ordinate system are (r,Ѳ,Ø). These surfaces are shown in figure
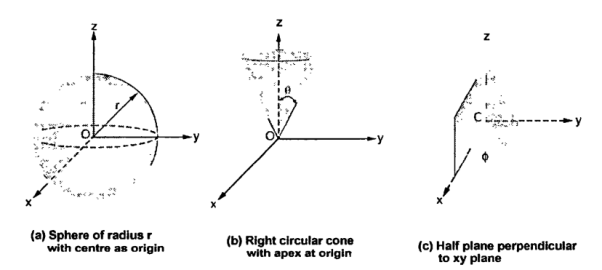
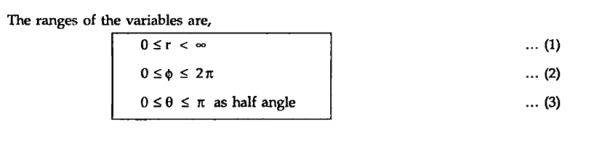
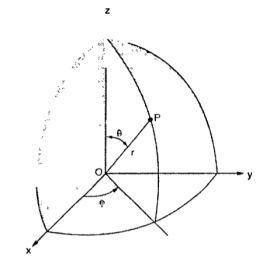
The point P(r,Ѳ,Ø) can be represented in the spherical co-ordinate system as shown in figure. The angles Ѳ and Ø are measured in radians. The point P can be defined as the intersection of three surfaces in spherical co-ordinate system. These three surfaces are:
r = Constant which is a sphere with cenre as origin
Ɵ = Constant which is right circular cone with apex as origin and axis a z axis
ɸ= Constant is a plane perpendicular to xy plane.
Base Vector :
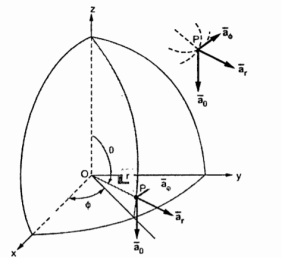
There are three-unit vectors in r, Ɵ and ɸ directions denoted as 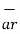 ,
, 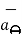 and
and 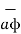 . These unit vectors are mutually perpendicular to each other as shown in figure. The unit vector
. These unit vectors are mutually perpendicular to each other as shown in figure. The unit vector 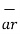 is directed from the centre of the sphere that is the origin to the given point P. It is radially outward normal to the sphere. It lies in the cone Ɵ = constant and plane ɸ= constant.
is directed from the centre of the sphere that is the origin to the given point P. It is radially outward normal to the sphere. It lies in the cone Ɵ = constant and plane ɸ= constant.
The unit vector 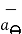 is tangent to the sphere and oriented in the direction of increasing Ɵ. It is normal to the conical surface.
is tangent to the sphere and oriented in the direction of increasing Ɵ. It is normal to the conical surface.
The third unit vector 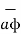 is tangent to the sphere and also tangent to the conical surface. It is oriented in the direction of increasing ɸ. It is same as defined in the cylindrical co-ordinate system.
is tangent to the sphere and also tangent to the conical surface. It is oriented in the direction of increasing ɸ. It is same as defined in the cylindrical co-ordinate system.
Hence, vector P is
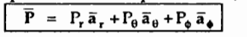
Differential elements in Spherical co-ordinate system.
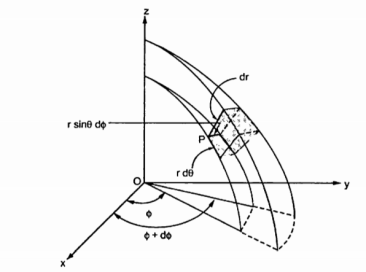
Consider a point P(r,Ɵ,ɸ) in spherical co-ordinate system. Let each co-ordinate be increased by the differential amount. The differential increments in r,Ɵ,ɸ are dr,dƟ and dɸ.
Now there are two spheres of radius r and r+dr . There are two cones with half angles Ɵ and Ɵ+dƟ. There are two planes at the angles ɸ+dɸ measured from xz plane. All these surfaces enclose a small volume as shown in figure.
Dr= Differential length in r direction
r d Ɵ = Differential length in Ɵ direction
r sin Ɵ dɸ = Differential length in ɸ direction.
Hence the differential vector length in spherical coordinate system is

The magnitude of the differential length vector is

Hence differential volume is given by
2. Vector Calculus
Differentiation
Consider a scalar valued function of scalar for example time -dependent density of a material 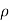 =
= 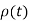
Consider vector valued function of scalar for example time -dependent displacement of a particle u = u(t). In this case the derivative in the usual way
Du/dt = lim ∆t->0 u(t+∆t) – u(t) / ∆t
Which turns out to be simply the derivative co-efficient
Du/dt = du1/dt e1 + du2/dt e2 + du3/dt = dui/dt ei
Partial differentiation:
Partial derivatives can also be defined . For example if u is a function of the coordinates u(x1,x2,x3) then
∂u/ ∂x1 = lim ∆x1->0 u(x1+ ∆x1 ,x2,x3) – u( x1,x2,x3) / ∆x1
Integration
The line integrals of vector fields as a line integral with respect to arc length as follows,
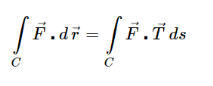
Where →T(t) is the unit tangent vector and is given by,
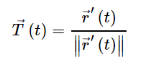
To compute line integrals with respect to arc length we can see that this second form is equivalent to the first form given above.
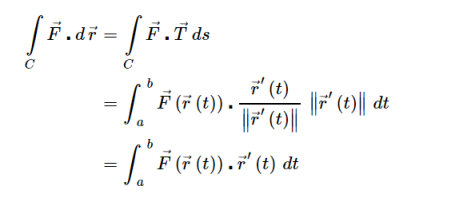
Vector operator del
Consider that in space let W be the unique function of x,y,z co-ordinates in the cartesian system. This is scalar function denoted as W(x,y,z) . Consider the vector operator in cartesian system denoted as 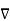 called del. It is defined as
called del. It is defined as
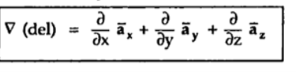
Gradient
Let ɸ(x) be a scalar field . The gradient of ɸ is vector field defined as
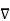 ɸ = ∂ɸ/ ∂x1 e1 + ∂ɸ2/∂x2 e2 + ∂ɸ3/∂x3 e3
ɸ = ∂ɸ/ ∂x1 e1 + ∂ɸ2/∂x2 e2 + ∂ɸ3/∂x3 e3
= ∂ɸ/∂xi ei = ∂ɸ/∂x. is important as it takes the dot product of 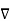 ɸ with dx it gives the increment in ɸ
ɸ with dx it gives the increment in ɸ
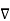 ɸ . dx = ∂ɸ/∂xi ei . Dxj ej
ɸ . dx = ∂ɸ/∂xi ei . Dxj ej
= ∂ɸ/∂xi . Dxi = dɸ
= ɸ(x+dx) - ɸ(dx)

Gradient of a vector
Properties:
The various properties of a gradient of a scalar field W are :
- The gradient
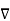 W gives the maximum rate of change of W per unit distance
W gives the maximum rate of change of W per unit distance - The gradient
 W always indicates the direction of the maximum rate of ch W.
W always indicates the direction of the maximum rate of ch W. - The gradient
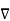 W at any point is perpendicular to the constant W surface passes through the point.
W at any point is perpendicular to the constant W surface passes through the point. - The directional derivative of W along the unit vector
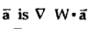 ( dot product which is the projection of
( dot product which is the projection of  W always indicates the direction of maximum rate of ch W.
W always indicates the direction of maximum rate of ch W.
Divergence:
It is seen that 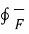 . d
. d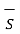 gives the flux flowing across the surface S. Then mathematically divergence is define as the net outward flow of the flux per unit volume of the flux per unit volume over a closed incremental surface. It is denoted as
gives the flux flowing across the surface S. Then mathematically divergence is define as the net outward flow of the flux per unit volume of the flux per unit volume over a closed incremental surface. It is denoted as
Div  = lim w->0
= lim w->0 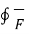 . d
. d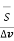 = Divergence of
= Divergence of 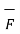
Curl
The circulation of a vector field around closed path is given by curl of vector. Mathematically it is defined as
Curl of 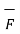 = lim ∆ SN ->0
= lim ∆ SN ->0  . d
. d
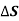 N = Area enclosed by the line integral in normal direction
N = Area enclosed by the line integral in normal direction
Thus, maximum circulation of 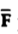 per unit area tends to zero whose direction is normal to the surface is called curl of
per unit area tends to zero whose direction is normal to the surface is called curl of 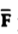 .
.
Symbolically it is represented as

3. Integral theorems of vectors
Stokes’ Theorem
For a simple region D with bounding curve C = ∂ D and two C’ fundtion P and Q on D we have
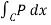 + Q dy =
+ Q dy = 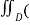 ∂Q/∂x - ∂P/∂y) dxdy
∂Q/∂x - ∂P/∂y) dxdy
Area of region is
A = 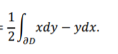
Gauss Divergence Theorem .
For a region W with boundary ∂W oriented by the outward pointing unit normal and if F is a smooth vector field defined on W then
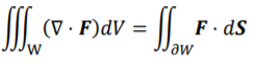
Transformation of vector from cylindrical to cartesian
 is the cylindrical system. Thus componnet
is the cylindrical system. Thus componnet 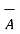 in
in 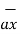 direction is given by
direction is given by
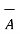 x = [
x = [ 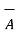 .
.  = [ Ar .
= [ Ar . 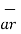 + A ɸ
+ A ɸ 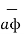 + Az
+ Az 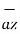 ]
] 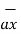
As dot product is commutative Hence ,
Ax = Ar cos ɸ - Aɸ sin ɸ
Ay = Ar sin ɸ+ Aɸ cos ɸ
Az = Az
Therefore,
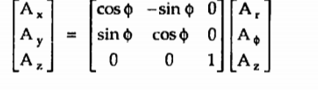
References:
- Faraday, Maxwell, and the Electromagnetic Field:by Basil Mahon and Nancy Forbes.
- ELECTROMAGNETISM: Theory and Applications Book by ASHUTOSH PRAMANIK
- Field and wave electromagnetics Textbook by David K. Cheng
Unit 1
Vector Algebra
The various mathematical operations such as addition, subtraction, multiplication etc can be performed with the vectors.
1.1.1 Addition of vectors:
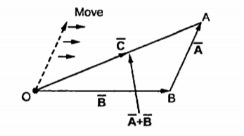
Consider two coplanar vectors as shown in figure. The vectors which lie in the same plane are called coplanar vectors.

Let us find the sum of these two vectors  and
and 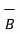 shown in figure. The procedure is to move one of the two vectors parallel to itself at the tip of the other vector. Thus, move
shown in figure. The procedure is to move one of the two vectors parallel to itself at the tip of the other vector. Thus, move 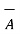 parallel to itself at the tip of
parallel to itself at the tip of 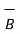 . Then join the tip of
. Then join the tip of  moved to the origin . This vector represents resultant which is the addition of the two vectors
moved to the origin . This vector represents resultant which is the addition of the two vectors  and
and 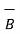 . This is shown in figure . The resultant
. This is shown in figure . The resultant 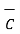 then is
then is  and
and 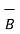
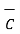 =
= 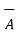 +
+ 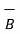
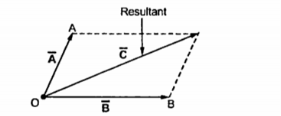
Another method of performing the addition of vectors is the parallelogram rule. Complete the parallelogram as shown in figure. Then the diagonal of the parallelogram represents the addition of two vectors.
1.1.2 Subtraction of Vectors
The subtraction of vectors can be obtained from the rules of addition. If 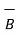
Is to be subtracted from 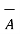 then based on addition it can be represented as ,
then based on addition it can be represented as ,
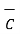 =
=  + (-
+ (- 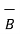 )
)
Thus, reverse the sign of 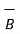 that is reverse its direction by multiplying it with -1and then add it to
that is reverse its direction by multiplying it with -1and then add it to 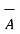 to obtain the subtraction. This is shown in the figure
to obtain the subtraction. This is shown in the figure

If 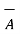 = 3 ax + 2 ay + 6 az and
= 3 ax + 2 ay + 6 az and 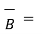 2 ax + 5 ay – 3az . Find
2 ax + 5 ay – 3az . Find
i) 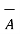 +
+ 
Ii) 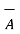 -
- 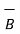
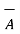 +
+ 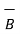 = 3
= 3 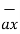 + 2
+ 2 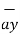 + 6
+ 6 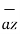 + 2
+ 2  + 5
+ 5  – 3
– 3 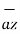 = 5
= 5 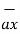 + 7
+ 7 + 3
+ 3 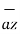
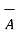 -
- 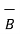 = 3
= 3 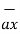 + 2
+ 2 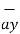 + 6
+ 6 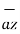 -( 2
-( 2 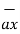 + 5
+ 5 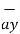 – 3
– 3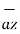 )
)
= 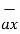 – 3
– 3 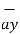 + 9
+ 9 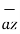
1.1.3 Components of vectors
To find the component of the vector in a given direction
Consider a vector 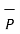 and the unit vector
and the unit vector  as shown in figure . The component of vector in
as shown in figure . The component of vector in  in the direction of unit vector
in the direction of unit vector 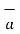 is
is 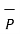 .
. 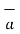 . This is the scalar quantity shown in figure (a)
. This is the scalar quantity shown in figure (a)
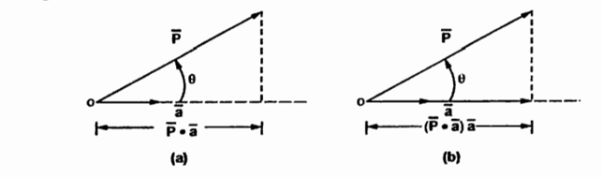
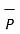 .
. 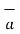 = |
= |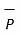 | |
| |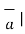 cos Ɵ = |
cos Ɵ = |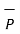 | cos Ɵ.
| cos Ɵ.
The sign of the component is positive if 0≤Ɵ≤ 90 o while the sign of this component is negative if 90 o <Ɵ≤ 180 o .
If the component vector of 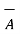 is in the direction of unit vector
is in the direction of unit vector 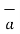 is required then multiply the component obtained by that unit vector as shown in fig(b). Thus
is required then multiply the component obtained by that unit vector as shown in fig(b). Thus
(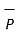 .
. 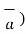
 is the component vector of
is the component vector of  in the direction of
in the direction of 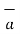 .
.
The component of 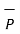 in the direction of
in the direction of 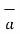 x is
x is 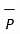 .
.  x that is Px while the component vector of
x that is Px while the component vector of 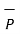 in the direction of
in the direction of 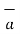 x is
x is 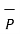 .
.  x
x
If the projection of  on the other vector
on the other vector 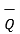 is obtained then it is necessary to find unit vector in the direction of
is obtained then it is necessary to find unit vector in the direction of 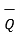 first that is
first that is 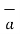 Q . Then the projection of
Q . Then the projection of  on
on 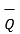 is given
is given 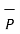 .
.  Q .
Q .
As 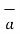 Q =
Q = 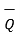 / |
/ |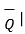 then the projection of
then the projection of 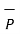 on
on  can be expressed as
can be expressed as
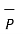 .
. 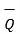 / |
/ |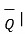 =
=  .
. 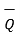 / |
/ |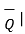
1.1.4 Scalar
If we multiply a vector ⃑A by a scalar k, we obtain a vector ⃑B such that
⃑B = 𝑘 ⃑A⃑
The magnitude of ⃑B is simply equal to |𝑘| times the magnitude of ⃑A .
If k < 0 then ⃑B in the opposite direction from ⃑A
If k > 0 then ⃑B in the same direction as ⃑A
So, vector ⃑B is said to be a dependent vector.
1.1.5 Vector Multiplication
There are two types of vector multiplication:
- Dot product(or) Scalar product
- Cross Product (or) Vector Product
Dot Product :

The scalar or dot of the two vectors  and
and 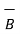 is denoted as
is denoted as  .
. 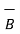 and defined as the product of the magnitude of A , the magnitude of B and the cosine of the smaller angle between them.
and defined as the product of the magnitude of A , the magnitude of B and the cosine of the smaller angle between them.
It also can defined as the product of magnitude of  and the projection of
and the projection of 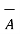 onto
onto 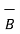 or vice versa.
or vice versa.
Mathematically it is expressed as,
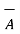 .
.  = |
= | |
|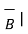 cos Ɵ AB --------------------------------------(1)
cos Ɵ AB --------------------------------------(1)
The result of such a dot product is scalar and hence called scalar product.
Properties of Dot Product
The various properties of the dot product are :
- If two vectors are parallel to each other Ɵ = 0 0 then cos Ɵ AB =1 thus
 .
. 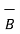 = |
= |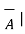 |
|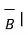 for parallel vectors -------------------------------------(2)
for parallel vectors -------------------------------------(2)
2. If the two vectors are perpendicular to each other Ɵ = 90 o then cos Ɵ AB =0 thus
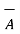 .
. 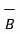 = 0 for perpendicular vectors ------------------------------(3)
= 0 for perpendicular vectors ------------------------------(3)
If the dot product of the two vectors is zero then the two vectors are perpendicular to each other.
The dot product obeys commutative law
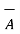 .
. 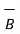 =
=  .
. 
3. The dot product obeys distributive law,
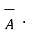 (
( 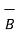 +
+ 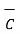 ) =
) = 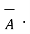
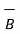 +
+ 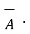

4. If the dot product of vector with itself is performed the result is the square of the magnitude of that vector.
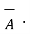
 = |
= |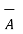 | |
| |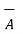 | cos 0 o = |
| cos 0 o = |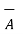 | 2
| 2
5. Consider the unit vectors 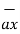 ,
,  ,
, 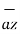 in cartesian co-ordinate system. All these vectors are mutually perpendicular to each other. Hence the dot product of different unit vectors is zero.
in cartesian co-ordinate system. All these vectors are mutually perpendicular to each other. Hence the dot product of different unit vectors is zero.
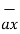 .
. 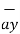 =
= 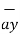 .
.  =
= 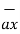 .
. 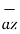 =
=  .
.  =
= 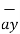 .
. 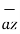 =
= 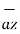 .
. 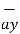 =0
=0
Any unit vector dotted with itself is unity
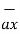 .
. 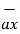 =
=  .
. 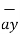 =
= 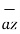 .
. 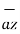 = 1
= 1
Applications of Dot Product :
The applications of dot product are :
1.To determine the angle between the two vectors .
The angle can be determined by
Ɵ = cos -1 { 
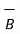 )/ |
)/ | | |
| |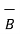 |}
|}
2. Physically work done by a constant force can be expressed as dot product of two vectors.
Consider a constant force  acting on a body and it causes the displacement
acting on a body and it causes the displacement 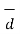 of that body. Then the work done W is the product of the force and the component of the displacement in the direction of force which can be expressed as ,
of that body. Then the work done W is the product of the force and the component of the displacement in the direction of force which can be expressed as ,
W = | d cos Ɵ =
d cos Ɵ = 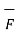 .
. 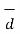 of that body. Then the work done W of the force and the component of the displacement in the direction of force which can be expressed as ,
of that body. Then the work done W of the force and the component of the displacement in the direction of force which can be expressed as ,
W = |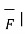 d cos Ɵ =
d cos Ɵ = 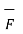 .
. 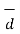
But if the force applied varies along the path then the total work done is to be calculated by the integration of a dot product as ,
W = 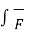 .
. 
Problem:
Given the two vectors ,
 = 2
= 2 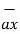 - 5
- 5  - 4
- 4  and
and 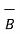 = 3
= 3 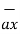 + 5
+ 5 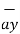 + 2
+ 2  . Find the dot product and the angle between the two vectors .
. Find the dot product and the angle between the two vectors .
The dot product is ,
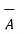 .
. 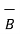 = Ax Bx + Ay By + Az Bz = (2x3) +(-5)(5) + (-4)(2) = -27
= Ax Bx + Ay By + Az Bz = (2x3) +(-5)(5) + (-4)(2) = -27
As 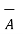 .
.  is negative it is expected that the angle between the two is greater than 90 o .
is negative it is expected that the angle between the two is greater than 90 o .
|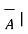 =
= 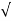 (2) 2 + (-5) 2 + (-4) 2 =
(2) 2 + (-5) 2 + (-4) 2 = 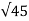
|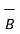 | =
| = 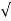 (3) 2 + (5) 2 + (2) 2 =
(3) 2 + (5) 2 + (2) 2 = 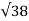
Ɵ= cos -1 {  .
. 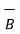 / |
/ |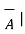 |
|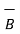 | } = cos -1 { -27 /
| } = cos -1 { -27 / 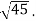
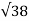 } = 130.762 o
} = 130.762 o
Given vector field 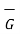 = (y-1)
= (y-1) 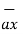 + 2x
+ 2x 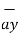 . Find this vector field at P(2,3,1) and its projection on
. Find this vector field at P(2,3,1) and its projection on 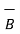 = 5
= 5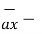
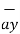 + 2
+ 2 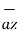 .
.
The field 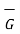 at point P is
at point P is
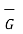 at P = 2
at P = 2 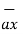
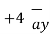 substituting co-ordinates of P in
substituting co-ordinates of P in 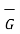
To find its projection on  first find
first find 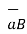 the unit vector in the direction of
the unit vector in the direction of 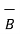
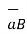 =
= 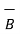 / |
/ |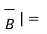 5
5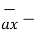
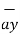 + 2
+ 2  /
/ 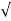 (5) 2 +(-1) 2 +(2) 2 = 0.9218
(5) 2 +(-1) 2 +(2) 2 = 0.9218 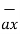 – 0.1825
– 0.1825 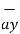 + 0.3651
+ 0.3651 
Hence projection of  at P on the vector
at P on the vector 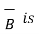
(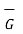 at P) .
at P) . 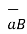 = (2x 0.9218)+(4x-0.1825)+(0x0.3651) = 1.0956.
= (2x 0.9218)+(4x-0.1825)+(0x0.3651) = 1.0956.
Cross Product :
Consider the two vectors 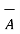 and
and 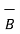 then the cross product is denoted as
then the cross product is denoted as 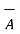 x
x  and defined as the product of the magnitudes
and defined as the product of the magnitudes 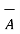 and
and 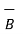 and the sine of the smaller angle between
and the sine of the smaller angle between 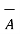 and
and 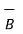 . But this product is a vector quantity and has a direction perpendicular to the plane containing the two vectors
. But this product is a vector quantity and has a direction perpendicular to the plane containing the two vectors 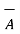 and
and 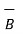
But for any plane there are two perpendicular directions upwards and downwards .
Mathematically
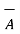 x
x 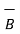 = |
= |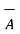 ||
||  | sin Ɵ AB
| sin Ɵ AB 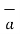 N where
N where  N = unit vector perpendicular to the plane of
N = unit vector perpendicular to the plane of 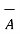 and
and 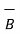 in the direction decided by the right hand screw rule.
in the direction decided by the right hand screw rule.
Properties of cross product are ,
- The commutative law is not applicable to the cross product. Thus
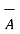 x
x 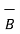 ≠
≠ 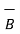 x
x 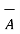
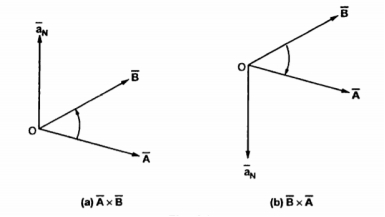
Consider two vectors shown in fig(a) . Then  x
x  gives unit vector
gives unit vector  N in the upward direction. But if
N in the upward direction. But if  x
x 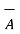 is obtained then direction of
is obtained then direction of 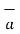 N must be determined by rotating
N must be determined by rotating  into
into 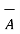 which results in down ward direction. This shown in fig(b) . Hence cross product is not commutative.
which results in down ward direction. This shown in fig(b) . Hence cross product is not commutative.
2. Reversing the order of the vectors 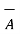 and
and 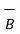 a unit vector
a unit vector 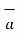 N reverses its direction. Hence we can write ,
N reverses its direction. Hence we can write ,
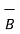 x
x 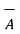 = -[
= -[ 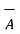 x
x 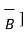
It is anticommutative in nature.
If order of cross product is changed , the magnitude remains the same but the direction is reversed.
3. The cross product is not associative.
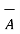 x
x 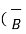 x
x  ) ≠ (
) ≠ ( 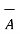 x
x 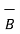 ) x
) x 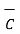
4. If the two vectors are parallel to each other that is they are in the same direction then Ɵ = 0 o and hence cross product of such two vectors is zero.
Thus if cross product of the two vectors is zero then those two vetors are parallel meaning same direction assuming none of the two vectors itself is zero.
5. If the cross product of vector 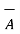 with itself is calculated it is zero as Ɵ = 0 o
with itself is calculated it is zero as Ɵ = 0 o
There fore  x
x 
Applications:
The different applications of cross product are:
- The cross product is the replacement to the right -hand rule to determine the direction of force experienced by current carrying conductor placed in a magnetic field. Thus, if I is the current flowing through conductor while
 is the vector length considered to indicate the direction of current through the conductor. The uniform magnetic flux density is denoted by
is the vector length considered to indicate the direction of current through the conductor. The uniform magnetic flux density is denoted by 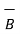 . Then the force experienced by conductor is given by
. Then the force experienced by conductor is given by
 = I
= I  x
x 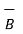
2. Another physical quantity which can be represented by cross product is the moment of force. The moment of force acting on the rigid body which can rotate about an axis perpendicular to a plane containing the force is defined to be the magnitude of the force multiplied by the perpendicular distance from the force to the axis is shown in figure.

The moment of force 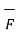 about a point O is
about a point O is 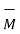 . Its magnitude is |
. Its magnitude is |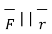 | sin Ɵ is the perpendicular distance of
| sin Ɵ is the perpendicular distance of 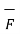 from O meaning OQ.
from O meaning OQ.
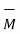 =
= 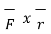 =
=  ||
||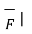 sin Ɵ
sin Ɵ 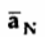 is the unit vector indicating direction of
is the unit vector indicating direction of 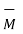 perpendicular to the plane.
perpendicular to the plane.
Problem :
Given the two coplanar vectors
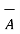 = 3
= 3 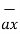 + 4
+ 4 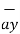 -5
-5 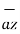 and
and 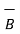 = -6
= -6  + 2
+ 2 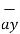 + 4
+ 4  . Obtain the unit vector normal to the plane containing vectors
. Obtain the unit vector normal to the plane containing vectors 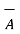 and
and 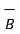

1.1.6 Triple Product
Let 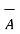 ,
, 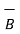 ,
,  be three given vectors. The product of these three vectors is classified in two ways called
be three given vectors. The product of these three vectors is classified in two ways called
- Scalar triple product 2. Vector triple product.
Scalar triple product :
The scalar triple product of three vectors 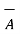 ,
, 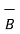 and
and 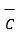 is defined as
is defined as
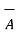 x (
x ( 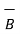 x
x 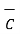 ) =
) =  . (
. ( 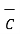 x
x 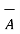 ) =
) =  . (
. ( 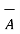 x
x  )
)
Thus if,
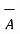 = Ax
= Ax 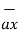 + Ay
+ Ay  + Az
+ Az 
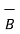 = Bx
= Bx 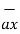 + By
+ By 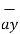 + Bz
+ Bz 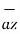
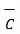 = Cx
= Cx  + Cy
+ Cy 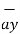 + Cz
+ Cz 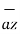
Then the scalar triple product is obtained by the determinant ,
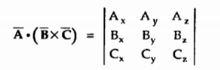
The result of this product is scalar hence the product is called scalar triple product.
Vector triple product
The vector triple product of the three vectors 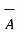 ,
, 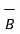 ,
,  is mathematically defined as
is mathematically defined as
 x(
x( 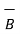 x
x  ) =
) = 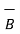 (
( 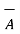 .
. 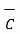 ) -
) - 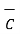 (
( 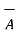 .
. 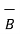 )
)
Characteristics of vector triple product :
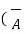 .
. 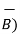
 ≠
≠ 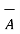 (
( 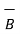 .
. 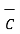 )
)
But  .
. 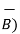
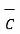 =
= 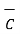 (
( 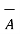 .
. 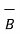 )
)
This is because  .
. 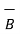 is a scalar and multiplication by scalar to a vector is commutative.
is a scalar and multiplication by scalar to a vector is commutative.
From the basic definition we can write,
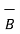 x(
x( 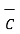 x
x 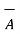 ) =
) = 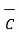 (
( 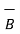 .
. 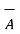 ) -
) - 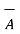 (
( 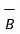 .
. 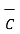 )
)
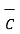 x(
x( 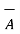 x
x 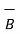 ) =
) = 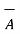 (
(  .
.  ) -
) - 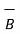 (
( 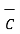 .
. 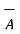 )
)
But the dot matrix is commutative hence  .
.  =
=  .
. 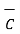 and so on. Hence,
and so on. Hence,
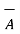 x(
x(  x
x  ) +
) + 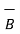 x(
x( 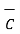 x
x 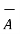 ) +
) + 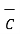 x(
x( 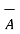 x
x  ) =0
) =0
The result of the vector triple product is a vector.
1.1.7 Three orthogonal coordinate systems
Rectangular:
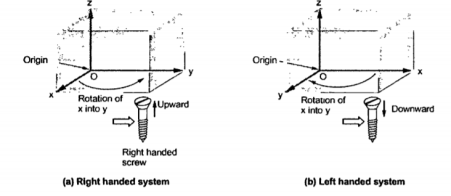
This system has three co-ordinate axes represented as x,y and z which are mutually at right angles to each other. These three axes intersect at common point called origin of the system. There are two types of such called
- Right- handed system 2. Left- handed system
The right- handed system means if x axis is rotated towards y axis through a smaller angle then this rotation causes upward movement of right- handed screw in the z-axis direction. This is shown in fig(a).
In this system if right hand is used then thumb indicates x-axis, forefinger indicates y-axis and middle finger indicates z-axis. When three fingers are held mutually perpendicular to each other.
In left-handed system x and y axes are interchanged compared to right-handed system. This means the rotation of x-axis through smaller angle causes the downward movement of right-handed screw in the z axis direction as shown in fig(b).
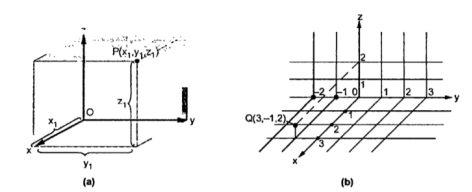
Representing a point in Rectangular Co-ordinate system
A point in rectangular co-ordinate system is located by three co-ordinates namely x,y and z co-ordinates. The point can be reached by moving from origin the distance of x in x-direction , distance of y in y-direction and finally distance of z in z direction.
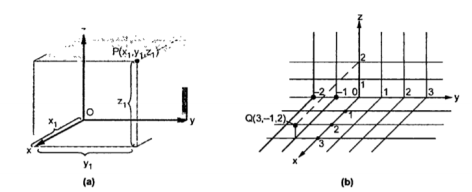
Consider a point P having co-ordinates x1,y1 and z1 which can be positive or negative.
The point Q(3,-1,2) can be shown as
Base vector :
The base vector are the unit vectors that are oriented along the directions of the co-ordinate axes of the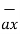 given co-ordinate system. Thus for cartesian co-ordinate system the three base vectors are unit vectors oriented in x,y and z axis of the system. Therefore
given co-ordinate system. Thus for cartesian co-ordinate system the three base vectors are unit vectors oriented in x,y and z axis of the system. Therefore  ,
, 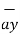 and
and 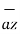 are the base vectors of the cartesian co-ordinate system.
are the base vectors of the cartesian co-ordinate system.
Any point of the x-axis having (x1,0,0) can be represented by a vector joining origin to this point to this point and denoted as x1 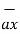 .
.
Position and Distance vectors :
Consider a point P(x1,y1,z1) in cartesian co-ordinate system as shown in figure. Then the position vector of point P from the origin directed from origin to point P. This is called radius vector as shown in figure.
The three components of position vector oriented along the three co-ordinate axes with magnitudes x1,y1and z1. Thus the position vector of point P can be represented as
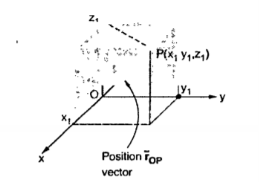
 OP = x1
OP = x1 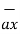 + y1
+ y1 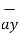 + z1
+ z1 
The magnitude of this vector in terms of three mutually perpendicular components is given by
|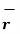 OP |=
OP |= 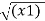 2 + (y1) 2 + (z1) 2
2 + (y1) 2 + (z1) 2
Thus, if point P has co-ordinates (1,2,3) then its position vector is
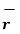 OP =1
OP =1 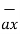 + 2
+ 2 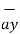 + 3
+ 3 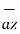
And
 OP =
OP = 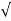 (1) 2 + (2) 2 + (3) 2 =
(1) 2 + (2) 2 + (3) 2 = 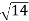 = 3.7416
= 3.7416
Consider two points in a cartesian coordinate system P and Q with the co-ordinates (x1,y1,z1) and (x2,y2,z2) respectively. The individual position vector of the points are
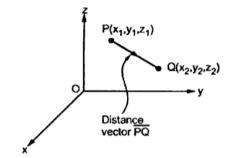
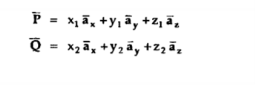
Then the displacement from P to Q is represented by the distance vector  and is given by
and is given by

This is called separation vector.
The magnitude of the vector is given by
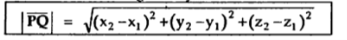
This is called as distance formula.
The unit vector along the direction PQ is given by

Obtain the unit vector in the direction from the origin towards the point P(3,-3,-2)
Solution:
The origin O(0,0,0) while P(3,-3,-2) hence the distance vector 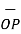 is
is
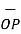 = (3-0)
= (3-0) 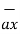 + (-3-0)
+ (-3-0)  +(-2-0)
+(-2-0) 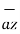 = 3
= 3 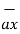 -3
-3 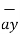 -2
-2 
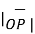 =
= 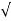 (3) 2 + (-3) 2 + (-2) 2 = 4.6904
(3) 2 + (-3) 2 + (-2) 2 = 4.6904
Hence the unit vector along the direction OP is
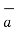 OP =
OP = 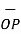 / |
/ |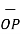 | = 3
| = 3 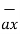 -3
-3  -2
-2  / 4.6904 =
/ 4.6904 =
= 0.6396 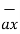 -0.63963
-0.63963 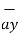 -0.4264
-0.4264 
Differential Elements in Cartesian Co-ordinate System
Consider a point P(x,y,z) in the rectangular co-ordinate system . If we increase each co-ordinate by a differential amount a new point P’ will be obtained having co-ordinates (x+dx, y +dy , z+dz)
Dx = differential length in x-direction
Dy = differential length in y-direction
Dz = differential length in z-direction
Hence differential vector length called elementary vector length
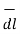 = dx
= dx 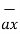 - dy
- dy 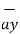 - dz
- dz 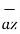 .
.
P is the intersection of the three planes and P’ is the intersection of the new three planes which are displaced from original three planes. These six planes together define a differential volume which is a rectangular parallelepiped as shown in the figure.
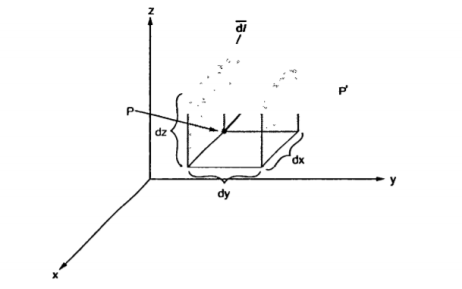
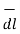 = dx
= dx 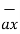 - dy
- dy 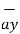 - dz
- dz  .
.
Hence the differential volume of the rectangular parallelepiped is given by
Dv = dx dy dz
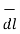 is vector and dv is scalar.
is vector and dv is scalar.
The differential surface area is given by
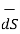 =
= 
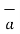 n
n
Ds = Different surfaces area of the element.
d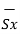 = Differential vector surface area normal to x direction dy dz
= Differential vector surface area normal to x direction dy dz 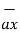
d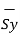 = = Differential vector surface area normal to y direction dx dz
= = Differential vector surface area normal to y direction dx dz 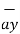
d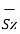 = = Differential vector surface area normal to y direction dx dy
= = Differential vector surface area normal to y direction dx dy 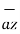
Given the three points in cartesian co-ordinate system as A(3,-2,1) B (-3,-3,5) , C (2,6,-4)
Find
i) The vector from A to C
Ii) The unit vector from B to A
Iii) The distance from B to C
Iv) The vector from A to the mid-point of the straight line joining B to C.
The position vectors for the given points are :
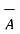 = 3
= 3  - 2
- 2 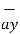 +
+ 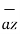 .
.
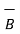 = -3
= -3 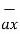 - 3
- 3 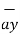 + 5
+ 5 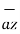 .
.
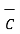 = 2
= 2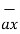 +6
+6 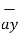 -4
-4 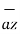 .
.
i) The vector from A to C is
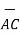 =
= 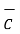 -
- 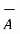 = [ 2-3]
= [ 2-3] 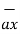 +[6 –(-2)]
+[6 –(-2)]  +[-4-1]
+[-4-1] 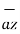 .
.
= - 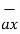 + 8
+ 8 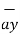 -5
-5 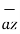 .
.
Ii) For unit vector from B to A obtain the distance vector 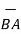 first
first
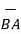 =
= 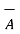 -
- 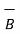
= [ 3 – (-3)]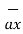 + [ (-2) –(-3) ]
+ [ (-2) –(-3) ] 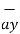 + [ -4-1]
+ [ -4-1] 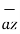
= 6 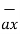 +
+  -4
-4  .
.
|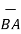 | =
| = 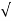 (6) 2 + (1) 2 + (-4)2 = 7.2801.
(6) 2 + (1) 2 + (-4)2 = 7.2801.
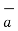 BA =
BA = 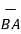 / |
/ |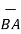 | = 6
| = 6 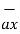 +
+ 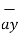 -4
-4 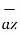 ./ 7.2801
./ 7.2801
Iii) For distance between B and C
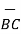 =
=  -
- 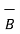 = [ 2 –(-3 ]
= [ 2 –(-3 ] 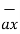 + [6-(-3)]
+ [6-(-3)] 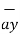 +[-4) –(-5)]
+[-4) –(-5)] 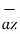 = 5
= 5 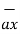 + 9
+ 9 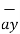 – 9
– 9 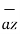
Distance BC = 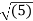 2 + (9) 2 + (-9) 2 = 13.6747
2 + (9) 2 + (-9) 2 = 13.6747
Iv) Let B(x1,y1,z1 ) and C(x2,y2,z2) then the co-ordinates of the mid-point BC are (x1+x2/2 , y1+y2/2 , z1+z2/2)
Cylindrical co-ordinate system
The circular cylindrical co-ordinate system is a three-dimensional version of polar co-ordinate system. The surfaces used to define the cylindrical co-ordinate system are :
- Plane of constant z which is parallel to xy plane.
- A cylinder of radius r with z-axis of the cylinder
- A half plane perpendicular to xy plane at angle Ø with respect to xz plane . The angle Ø is called the azimuth angle.
The ranges of the variable are :
0 ≤ r ≤ ∞------------------(1)
0 ≤Ø≤ 2π------------------------------(2)
-∞≤z≤∞--------------------------------------------------(3)
The point P in cylindrical co-ordinate system has three co-ordinates r, Ø and z whose values lie in the ranges given by equations 1,2,3.
The point P(r,Ø1,z1) can be shown in figure (b)
The point P can be defined as the intersection of three surfaces in cylindrical co-ordinate system. These three surfaces are,
r = Constant which is circular cylinder with z axis as its axis
Ø= Constant plane which is a vertical plane perpendicular to xy plane making angle Ø with respect to xz plane.
z= Constant plane is a plane parallel to xy plane.
These surfaces are shown in figure.

The intersction of any two surfaces out of the above three surfaces is either a line or a circle and intersection of three surfaces define a point.
The intersection of z=constant and r=constant is a circle. The intersection of ɸ=constant and r=constant is a line. The point P which is intersection of all three surfaces is shown in the figure.
Base vectors:
These are mutually perpendicular to each other. The  lies in a plane parallel to xy plane and perpendicular to the surface of the cylinder at a given point coming radially outwards. The vector
lies in a plane parallel to xy plane and perpendicular to the surface of the cylinder at a given point coming radially outwards. The vector 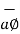 lies also in a plane parallel to xy plane but it is tangent to the cylinder and pointing in the direction of increasing
lies also in a plane parallel to xy plane but it is tangent to the cylinder and pointing in the direction of increasing  at the given point.
at the given point.
The unit vector 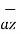 is parallel to z-axis and directed towards increasing z . Hence, vector of point P can be represented as
is parallel to z-axis and directed towards increasing z . Hence, vector of point P can be represented as
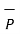 = P r
= P r 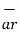 + P ɸ
+ P ɸ 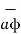 + P z
+ P z 
Differential Elements in Cylindrical co-ordinate system
Consider o point P(r,ɸ,z) in a cylindrical co-ordinate system. Let each co-ordinate be increased by differential amount. The differential increments in r,ɸ,z are dr,dɸ and dz respectively.
There are two cylinders of radius r and r+dr. There are two radial planes at the angles ɸ and ɸ+dɸ. And there are two horizontal planes at the heights z+dz. All these surfaces enclose a small volume as shown in figure.
The different lengths in r and z are dz and dr respectively. In ɸ direction dɸ is the change in angle ɸ and is not the differential length. Due to this change dɸ there exists a differential arc length in ɸ direction. This differential length due to dɸ in ɸ direction is r dɸ as shown in figure.
Thus the differential lengths are :
Dr = Differential length in r direction.
r dɸ = Differential length in ɸ direction
Dz = Differential length in z direction
Hence the differential vector length in cylindrical co-ordinate system is given by
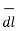 = dr
= dr 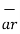 + r dɸ
+ r dɸ  + dz
+ dz 
The magnitude of the differential length vector is given y
|
 (dr) 2 +( r d ɸ) 2 + (dz) 2
(dr) 2 +( r d ɸ) 2 + (dz) 2
Hence the differential volume of the differential element is given by
Dv = r dr dɸ dz
Spherical co-ordinate system:
The surfaces which are used to define the spherical co-ordinate system on the three cartesian axes are:
- Sphere of radius r, origin as the centre of the sphere.
- A right circular cone with its apex at the origin and its axis as z-axis. It half angle is Ѳ varies from 0 to 180.
- A half plane perpendicular to xy plane containing z axis making an angle Ø with xz plane.
Thus the three co-ordinates of a point P in the spherical co-ordinate system are (r,Ѳ,Ø). These surfaces are shown in figure
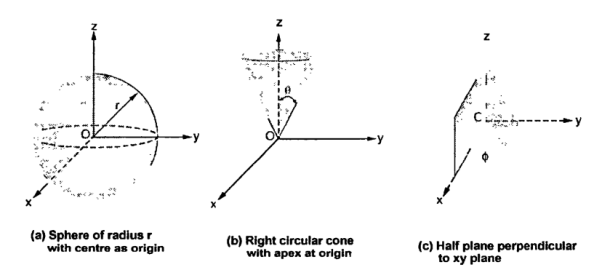
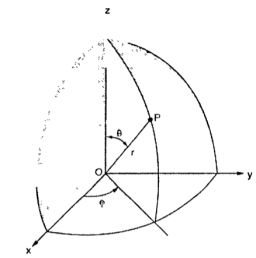
The point P(r,Ѳ,Ø) can be represented in the spherical co-ordinate system as shown in figure. The angles Ѳ and Ø are measured in radians. The point P can be defined as the intersection of three surfaces in spherical co-ordinate system. These three surfaces are:
r = Constant which is a sphere with cenre as origin
Ɵ = Constant which is right circular cone with apex as origin and axis a z axis
ɸ= Constant is a plane perpendicular to xy plane.
Base Vector :

There are three-unit vectors in r, Ɵ and ɸ directions denoted as  ,
, 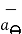 and
and  . These unit vectors are mutually perpendicular to each other as shown in figure. The unit vector
. These unit vectors are mutually perpendicular to each other as shown in figure. The unit vector 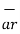 is directed from the centre of the sphere that is the origin to the given point P. It is radially outward normal to the sphere. It lies in the cone Ɵ = constant and plane ɸ= constant.
is directed from the centre of the sphere that is the origin to the given point P. It is radially outward normal to the sphere. It lies in the cone Ɵ = constant and plane ɸ= constant.
The unit vector 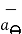 is tangent to the sphere and oriented in the direction of increasing Ɵ. It is normal to the conical surface.
is tangent to the sphere and oriented in the direction of increasing Ɵ. It is normal to the conical surface.
The third unit vector 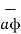 is tangent to the sphere and also tangent to the conical surface. It is oriented in the direction of increasing ɸ. It is same as defined in the cylindrical co-ordinate system.
is tangent to the sphere and also tangent to the conical surface. It is oriented in the direction of increasing ɸ. It is same as defined in the cylindrical co-ordinate system.
Hence, vector P is
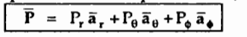
Differential elements in Spherical co-ordinate system.
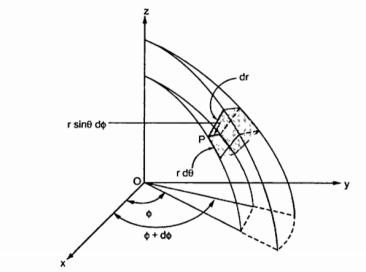
Consider a point P(r,Ɵ,ɸ) in spherical co-ordinate system. Let each co-ordinate be increased by the differential amount. The differential increments in r,Ɵ,ɸ are dr,dƟ and dɸ.
Now there are two spheres of radius r and r+dr . There are two cones with half angles Ɵ and Ɵ+dƟ. There are two planes at the angles ɸ+dɸ measured from xz plane. All these surfaces enclose a small volume as shown in figure.
Dr= Differential length in r direction
r d Ɵ = Differential length in Ɵ direction
r sin Ɵ dɸ = Differential length in ɸ direction.
Hence the differential vector length in spherical coordinate system is

The magnitude of the differential length vector is
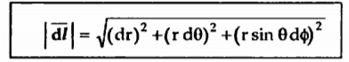
Hence differential volume is given by
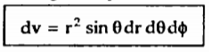
2. Vector Calculus
Differentiation
Consider a scalar valued function of scalar for example time -dependent density of a material 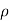 =
= 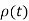
Consider vector valued function of scalar for example time -dependent displacement of a particle u = u(t). In this case the derivative in the usual way
Du/dt = lim ∆t->0 u(t+∆t) – u(t) / ∆t
Which turns out to be simply the derivative co-efficient
Du/dt = du1/dt e1 + du2/dt e2 + du3/dt = dui/dt ei
Partial differentiation:
Partial derivatives can also be defined . For example if u is a function of the coordinates u(x1,x2,x3) then
∂u/ ∂x1 = lim ∆x1->0 u(x1+ ∆x1 ,x2,x3) – u( x1,x2,x3) / ∆x1
Integration
The line integrals of vector fields as a line integral with respect to arc length as follows,

Where →T(t) is the unit tangent vector and is given by,
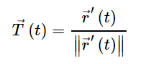
To compute line integrals with respect to arc length we can see that this second form is equivalent to the first form given above.
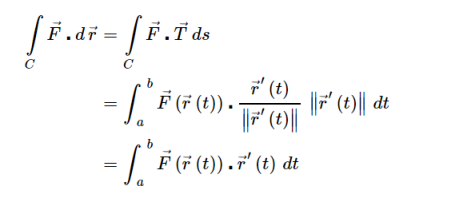
Vector operator del
Consider that in space let W be the unique function of x,y,z co-ordinates in the cartesian system. This is scalar function denoted as W(x,y,z) . Consider the vector operator in cartesian system denoted as 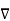 called del. It is defined as
called del. It is defined as
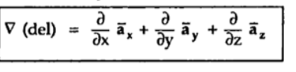
Gradient
Let ɸ(x) be a scalar field . The gradient of ɸ is vector field defined as
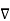 ɸ = ∂ɸ/ ∂x1 e1 + ∂ɸ2/∂x2 e2 + ∂ɸ3/∂x3 e3
ɸ = ∂ɸ/ ∂x1 e1 + ∂ɸ2/∂x2 e2 + ∂ɸ3/∂x3 e3
= ∂ɸ/∂xi ei = ∂ɸ/∂x. is important as it takes the dot product of 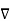 ɸ with dx it gives the increment in ɸ
ɸ with dx it gives the increment in ɸ
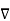 ɸ . dx = ∂ɸ/∂xi ei . Dxj ej
ɸ . dx = ∂ɸ/∂xi ei . Dxj ej
= ∂ɸ/∂xi . Dxi = dɸ
= ɸ(x+dx) - ɸ(dx)

Gradient of a vector
Properties:
The various properties of a gradient of a scalar field W are :
- The gradient
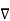 W gives the maximum rate of change of W per unit distance
W gives the maximum rate of change of W per unit distance - The gradient
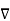 W always indicates the direction of the maximum rate of ch W.
W always indicates the direction of the maximum rate of ch W. - The gradient
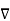 W at any point is perpendicular to the constant W surface passes through the point.
W at any point is perpendicular to the constant W surface passes through the point. - The directional derivative of W along the unit vector
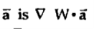 ( dot product which is the projection of
( dot product which is the projection of 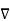 W always indicates the direction of maximum rate of ch W.
W always indicates the direction of maximum rate of ch W.
Divergence:
It is seen that 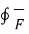 . d
. d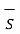 gives the flux flowing across the surface S. Then mathematically divergence is define as the net outward flow of the flux per unit volume of the flux per unit volume over a closed incremental surface. It is denoted as
gives the flux flowing across the surface S. Then mathematically divergence is define as the net outward flow of the flux per unit volume of the flux per unit volume over a closed incremental surface. It is denoted as
Div 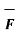 = lim w->0
= lim w->0 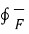 . d
. d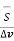 = Divergence of
= Divergence of 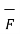
Curl
The circulation of a vector field around closed path is given by curl of vector. Mathematically it is defined as
Curl of 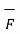 = lim ∆ SN ->0
= lim ∆ SN ->0 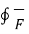 . d
. d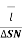
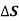 N = Area enclosed by the line integral in normal direction
N = Area enclosed by the line integral in normal direction
Thus, maximum circulation of 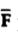 per unit area tends to zero whose direction is normal to the surface is called curl of
per unit area tends to zero whose direction is normal to the surface is called curl of 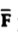 .
.
Symbolically it is represented as

3. Integral theorems of vectors
Stokes’ Theorem
For a simple region D with bounding curve C = ∂ D and two C’ fundtion P and Q on D we have
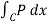 + Q dy =
+ Q dy = 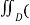 ∂Q/∂x - ∂P/∂y) dxdy
∂Q/∂x - ∂P/∂y) dxdy
Area of region is
A = 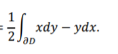
Gauss Divergence Theorem .
For a region W with boundary ∂W oriented by the outward pointing unit normal and if F is a smooth vector field defined on W then

Transformation of vector from cylindrical to cartesian
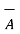 is the cylindrical system. Thus componnet
is the cylindrical system. Thus componnet 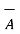 in
in 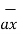 direction is given by
direction is given by
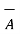 x = [
x = [ 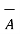 .
. 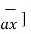 = [ Ar .
= [ Ar . 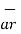 + A ɸ
+ A ɸ 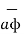 + Az
+ Az 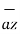 ]
] 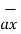
As dot product is commutative Hence ,
Ax = Ar cos ɸ - Aɸ sin ɸ
Ay = Ar sin ɸ+ Aɸ cos ɸ
Az = Az
Therefore,

References:
- Faraday, Maxwell, and the Electromagnetic Field:by Basil Mahon and Nancy Forbes.
- ELECTROMAGNETISM: Theory and Applications Book by ASHUTOSH PRAMANIK
- Field and wave electromagnetics Textbook by David K. Cheng