Module 3
Conductors, Dielectrics and Capacitances
The current is defined as the rate of flow of charge and is measured in amperes. The current is considered to be the motion of the positive charges. Hence the direction of the conventional current is assumed to be opposite to the direction of flow of the electrons.
The current which exists in the conductors due to the drifting of electrons under the influence of the applied voltage is called drift current.
While in dielectrics, there can be flow of charges under the influence of the electric field intensity. Such a current is called displacement current or convection current. The current flowing across the capacitor through the dielectric separating its plates is an example of convection current.
The analysis of such currents in the field theory is based on defining a current density at a point in the field.
The current density is a vector quantity associated with the current and denoted as 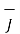 . The current density is measured in amperes per square meters.
. The current density is measured in amperes per square meters.
The relationship between 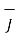 and
and 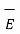 can also be expressed in terms of conductivity of the material.
can also be expressed in terms of conductivity of the material.
Thus for a metallic conductor,
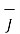 =
= 
 where
where  = Conductivity of the material.
= Conductivity of the material.
The conductivity is measured in mhos per metre. The equation is called point form of Ohm’s law . The unit of conductivity is also called Siemens per metre (S/m)
The continuity of current is based on the principle of conservation of charge. The principle states that ,
The charges can neither be created nor be destroyed.
Consider a closed surface S with current density 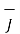 then the total current I crossing the surface is given by
then the total current I crossing the surface is given by
I =  . d
. d 
The current flows outwards from the closed surface. Hence current I is constituted due to outward flow of positive charges from the closed surface.
According to principle of conservation of energy there must be decrease of an equal amount of positive charge inside the closed surface. Hence the outward rate of flow of positive charge gets balanced by the rate of decrease of charge inside the closed surface.
Let Qi = charge within the closed surface
DQi/dt = Rate of decrease of charge inside the closed surface.
The negative sign indicates the decrease of charge.
Due to the principle of conservation of energy this rate of decrease is same as the rate of outward flow of charge which is a current.
I = 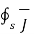 . d
. d  = -dQi/dt
= -dQi/dt
This is the integral form of the continuity equation of current.
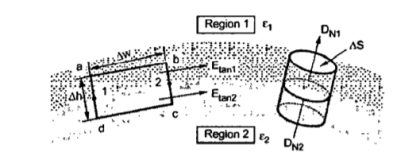
Let us consider the boundary between two perfect dielectrics. One dielectric has permittivity  while the other has permittivity
while the other has permittivity  . The interface is as shown in figure.
. The interface is as shown in figure.
The 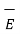 and
and 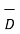 are obtained again by resolving each into two components tangential to the boundary and normal to the surface.
are obtained again by resolving each into two components tangential to the boundary and normal to the surface.
Consider a closed path abcda rectangular in shape having elementary height ∆h and elementary width ∆h as shown in figure. It is placed in such a way that ∆h/2 is in dielectric 1 while the remaining dielectric 2. Let us evaluate the integral 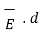
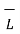
Along this path tracing it in clockwise direction as a-b-c-d-a.
 . d
. d 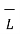 = 0
= 0
 . d
. d 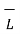 +
+ 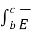 . d
. d  +
+ 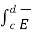 . d
. d 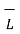 +
+ 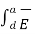 . d
. d  =0
=0
Now  =
= 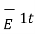 +
+  1N
1N
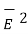 =
= 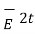 +
+  2N
2N
Both 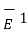 and
and 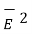 in the respective dielectrics have both the components, normal and tangential .
in the respective dielectrics have both the components, normal and tangential .
Let |  | = E tan1 |
| = E tan1 | 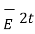 | = E tan 2
| = E tan 2
| 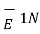 | = E 1N |
| = E 1N |  | = E 2N
| = E 2N
Now for rectangle to be reduced at the surface to analyse boundary conditions ∆h->0 . As ∆h->0 the equation reduces to
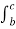 and
and  become zero as these are line integrals along ∆h and ∆h ->0.
become zero as these are line integrals along ∆h and ∆h ->0.
Hence equation reduces to
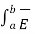 . d
. d 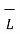 +
+ 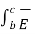 . d
. d  =0
=0
Now a-b is in dielectric 1 hence the corresponding component of 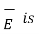 E tan1 as a-b direction is tangential to the surface.
E tan1 as a-b direction is tangential to the surface.
 . d
. d  = E tan1
= E tan1  = E tan1 ∆w
= E tan1 ∆w
Now a-b is in dielectric 1 hence the corresponding component of 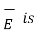 E tan1 as a-b direction is tangential to the surface.
E tan1 as a-b direction is tangential to the surface.
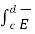 . d
. d  = E tan2 ∆w
= E tan2 ∆w
E tan1 ∆w - E tan2 ∆w =0
E tan1 = E tan2 ∆w
Thus the tangential components of field intensity at the boundary in both the dielectric remains same that is electric field intensity is continuous across the boundary.


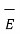
Hence if D tan1 and D tan2 are magnitudes of the tangential components of  in dielectric 1 and 2 respectively then
in dielectric 1 and 2 respectively then
D tan1 = 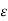

Hence if D tan1 and D tan2 are magnitudes of the tangential components of 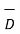 in dielectric 1 and 2 respectively then
in dielectric 1 and 2 respectively then
D tan1 =  E tan1 and D tan2 =
E tan1 and D tan2 = 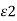 E tan2
E tan2
D tan1/ 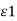 = D tan2 /
= D tan2 / 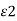
Dtan1/ Dtan2 = 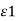 / /
/ / 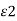 = /
= / 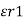 / /
/ / 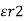
Thus tangential components of  undergoes some change across the interface hence tangential
undergoes some change across the interface hence tangential 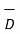 undergoes some change across the interface hence tangential
undergoes some change across the interface hence tangential  is said to be discontinuous across the boundary.
is said to be discontinuous across the boundary.
To find the normal components we need to use Gauss’s law. Consider a Gaussian surface in the form of right circular cylinder placed in such a way that half of it lies in dielectric 1 while the remaining half in dielectric 2. The height ∆h ->0 hence flux leaving from its lateral surface is zero. The surface area of its top and bottom is ∆S.
 . d
. d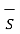 = Q
= Q
[ 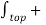

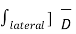 . d
. d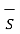 = Q
= Q
But  . d
. d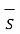 =0 as ∆h ->0
=0 as ∆h ->0
 . d
. d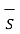 +
+  . d
. d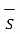 = Q
= Q
The flux leaving normal to the boundary to the top and bottom surfaces.
|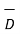 | = DN1 for dielectric 1 and DN2 for dielectric 2.
| = DN1 for dielectric 1 and DN2 for dielectric 2.
As top and bottom surfaces are elementary flux density can be assumed constant and can be taken out of integration
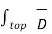 . d
. d = DN1
= DN1 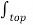 . d
. d = DN1 ∆ S
= DN1 ∆ S
For top surface the direction DN is entering the boundary while for bottom surface
|D| = DN1 for dielectric 1 and DN2 for dielectric 2
And as top and bottom surfaces are elementary flux density can be assumed constant and can be taken out of integration.
 . d
. d 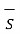 = DN1
= DN1  . d
. d 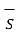 = DN1 ∆S
= DN1 ∆S
For top surface the direction of DN is entering the boundary while for bottom surface the direction of DN is leaving the boundary. Both are opposite in direction at the boundary.
 . d
. d  = -DN2
= -DN2  . d
. d 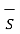 = -DN2 ∆S
= -DN2 ∆S
DN1 ∆S - DN2 ∆S = Q
But Q =  ∆S
∆S
DN1 - DN2 = = 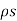
Consider two conducting materials M1 and M2 which are placed in a dielectric medium having permittivity  . The material M1 carries a positive charge Q while the material M2 carries a negative charge equal in magnitude as Q. There are no other charges present and the total charge of the system is zero.
. The material M1 carries a positive charge Q while the material M2 carries a negative charge equal in magnitude as Q. There are no other charges present and the total charge of the system is zero.
In conductors, charges cannot reside within the conductor and it resides only on the surface. Thus, for M1 and M2 charges +Q and -Q reside on the surfaces M1 and M2 respectively. This is shown in figure.

Capacitance
Such a system which has two conducting surfaces carrying equal and opposite charges separated by a dielectric is called capacitive system giving rise to capacitance.
The electric field is normal to the conductor surface and the electric flux is directed from M1 and M2 in such a system. There exists a potential difference between the two surfaces of M1 and M2. Let this potential be V12. The ratio of magnitudes of the total charge on any one of the two conductors and the potential difference between the conductors is called capacitance of the two-conductor system denoted as C.
C = Q/ V12
In general C =Q/V
Where Q = charge in coulombs
V = Potential difference in volts.
The capacitance is measured in farads.
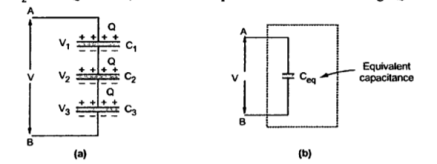
Consider the three capacitors in series connected across the applied voltage V as shown in figure.
Suppose this pushes charge Q on C1 then the opposite plate of C1 must have the same charge. This charge which is negative must have been obtained from the connecting leads by the charge separation which means that the charge on the upper plate of C2 is also Q . In short all the three capacitors have the same charge Q.

Q = C1 V1 = C2 V2 = C3 V3
V1 = Q/C1 ; V2 = Q/C2 ; V3 = Q/C3
If an equivalent capacitor stores the same charge when applied with same voltage
Ceq = Q/V or V = Q/Ceq
But V = V1 + V2 + V3
Q/Ceq = Q/C1 + Q/C2 + Q/C3
1/Ceq = 1/C1 + 1/C2 + 1/C3
For n capacitors in series
1/Ceq = 1/C1 + 1/C2 +……………….+ 1/Cn.
From the Gauss’s law in the point form Poisson’s equation can be derived. Consider the Gauss’s law in the point form as
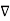 .
. 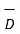 =
= 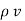
 = flux density
= flux density
 Volume charge density.
Volume charge density.
For a homogeneous isotropic and linear medium, flux density and the electric field are directly proportional. Thus,
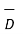 =
=  .
. 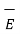
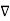 .
. 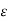 .
. 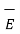 =
= 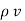
From the gradient relationship
E = -  . V
. V
 .
. 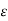 (-
(-  . V) =
. V) = 
 (
( 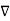 .
. 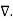 V) =
V) = 
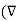 .
.  V) =-
V) =- 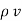 /
/ 
Now 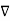 .
.  operation is called ‘del squared’ operation denoted as
operation is called ‘del squared’ operation denoted as 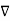 2.
2.
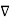 2. V = -
2. V = -  /
/ 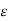
This equation is called as Poisson’s Equation
If in a certain region volume charge density is zero ( 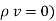 which is true for dielectric medium then the Poisson’s equation takes the form,
which is true for dielectric medium then the Poisson’s equation takes the form,
 2. V =0.
2. V =0.
This equation is called Laplace’s equation.
The procedure to solve a problem involving Laplace’s equation is :
Step 1: Solve the Laplace equation using the method of integration. Assume constants of integration.
Step2. Determine the constants by applying the boundary conditions given or known for the region. The solution obtained in step1 with constants obtained using boundary conditions is an unique solution.
Step 3: Then 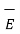 can be obtained for the potential field V obtained using gradient operation -
can be obtained for the potential field V obtained using gradient operation -  V.
V.
Step 4. For homogeneous medium  can be obtained as
can be obtained as 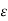
 .
.
Step 5: At the surface 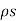 = DN hence
= DN hence 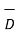 is known. The normal component DN to the surface is known. Hence the charged induced on the conductor surface can be obtained as
is known. The normal component DN to the surface is known. Hence the charged induced on the conductor surface can be obtained as
Q = - 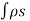 dS
dS
Step 6: Once the charged induced Q is known and potential V is known then the capacitance C of the system can be obtained.
If 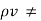 0 then the same procedure can be obtained to solve Poisson’s equation.
0 then the same procedure can be obtained to solve Poisson’s equation.
Using Laplace or Poisson’s equation we obtain:
- Potential at any point in between two surfaces when potential at two surface are given.
- We can also obtain capacitance between these two surfaces.
References:
- Faraday, Maxwell, and the Electromagnetic Field:by Basil Mahon and Nancy Forbes.
- ELECTROMAGNETISM: Theory and Applications Book by ASHUTOSH PRAMANIK
- Field and wave electromagnetics Textbook by David K. Cheng
Module 3
Conductors, Dielectrics and Capacitances
The current is defined as the rate of flow of charge and is measured in amperes. The current is considered to be the motion of the positive charges. Hence the direction of the conventional current is assumed to be opposite to the direction of flow of the electrons.
The current which exists in the conductors due to the drifting of electrons under the influence of the applied voltage is called drift current.
While in dielectrics, there can be flow of charges under the influence of the electric field intensity. Such a current is called displacement current or convection current. The current flowing across the capacitor through the dielectric separating its plates is an example of convection current.
The analysis of such currents in the field theory is based on defining a current density at a point in the field.
The current density is a vector quantity associated with the current and denoted as  . The current density is measured in amperes per square meters.
. The current density is measured in amperes per square meters.
The relationship between 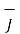 and
and 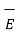 can also be expressed in terms of conductivity of the material.
can also be expressed in terms of conductivity of the material.
Thus for a metallic conductor,
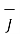 =
= 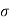
 where
where 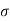 = Conductivity of the material.
= Conductivity of the material.
The conductivity is measured in mhos per metre. The equation is called point form of Ohm’s law . The unit of conductivity is also called Siemens per metre (S/m)
The continuity of current is based on the principle of conservation of charge. The principle states that ,
The charges can neither be created nor be destroyed.
Consider a closed surface S with current density  then the total current I crossing the surface is given by
then the total current I crossing the surface is given by
I = 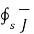 . d
. d 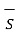
The current flows outwards from the closed surface. Hence current I is constituted due to outward flow of positive charges from the closed surface.
According to principle of conservation of energy there must be decrease of an equal amount of positive charge inside the closed surface. Hence the outward rate of flow of positive charge gets balanced by the rate of decrease of charge inside the closed surface.
Let Qi = charge within the closed surface
DQi/dt = Rate of decrease of charge inside the closed surface.
The negative sign indicates the decrease of charge.
Due to the principle of conservation of energy this rate of decrease is same as the rate of outward flow of charge which is a current.
I = 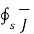 . d
. d 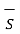 = -dQi/dt
= -dQi/dt
This is the integral form of the continuity equation of current.
Let us consider the boundary between two perfect dielectrics. One dielectric has permittivity 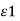 while the other has permittivity
while the other has permittivity 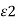 . The interface is as shown in figure.
. The interface is as shown in figure.

The  and
and 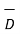 are obtained again by resolving each into two components tangential to the boundary and normal to the surface.
are obtained again by resolving each into two components tangential to the boundary and normal to the surface.
Consider a closed path abcda rectangular in shape having elementary height ∆h and elementary width ∆h as shown in figure. It is placed in such a way that ∆h/2 is in dielectric 1 while the remaining dielectric 2. Let us evaluate the integral 
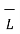
Along this path tracing it in clockwise direction as a-b-c-d-a.
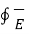 . d
. d 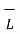 = 0
= 0
 . d
. d 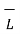 +
+ 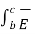 . d
. d 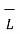 +
+ 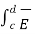 . d
. d 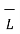 +
+  . d
. d  =0
=0
Now 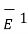 =
=  +
+ 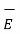 1N
1N
 =
= 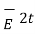 +
+ 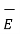 2N
2N
Both 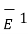 and
and  in the respective dielectrics have both the components, normal and tangential .
in the respective dielectrics have both the components, normal and tangential .
Let | 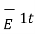 | = E tan1 |
| = E tan1 | 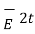 | = E tan 2
| = E tan 2
| 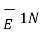 | = E 1N |
| = E 1N | 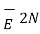 | = E 2N
| = E 2N
Now for rectangle to be reduced at the surface to analyse boundary conditions ∆h->0 . As ∆h->0 the equation reduces to
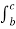 and
and 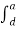 become zero as these are line integrals along ∆h and ∆h ->0.
become zero as these are line integrals along ∆h and ∆h ->0.
Hence equation reduces to
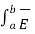 . d
. d 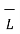 +
+ 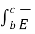 . d
. d  =0
=0
Now a-b is in dielectric 1 hence the corresponding component of 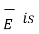 E tan1 as a-b direction is tangential to the surface.
E tan1 as a-b direction is tangential to the surface.
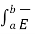 . d
. d  = E tan1
= E tan1 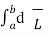 = E tan1 ∆w
= E tan1 ∆w
Now a-b is in dielectric 1 hence the corresponding component of 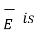 E tan1 as a-b direction is tangential to the surface.
E tan1 as a-b direction is tangential to the surface.
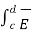 . d
. d 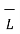 = E tan2 ∆w
= E tan2 ∆w
E tan1 ∆w - E tan2 ∆w =0
E tan1 = E tan2 ∆w
Thus the tangential components of field intensity at the boundary in both the dielectric remains same that is electric field intensity is continuous across the boundary.
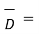
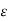
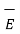
Hence if D tan1 and D tan2 are magnitudes of the tangential components of 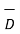 in dielectric 1 and 2 respectively then
in dielectric 1 and 2 respectively then
D tan1 = 

Hence if D tan1 and D tan2 are magnitudes of the tangential components of 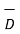 in dielectric 1 and 2 respectively then
in dielectric 1 and 2 respectively then
D tan1 = 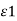 E tan1 and D tan2 =
E tan1 and D tan2 = 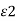 E tan2
E tan2
D tan1/ 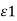 = D tan2 /
= D tan2 / 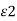
Dtan1/ Dtan2 =  / /
/ / 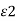 = /
= /  / /
/ / 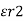
Thus tangential components of  undergoes some change across the interface hence tangential
undergoes some change across the interface hence tangential 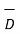 undergoes some change across the interface hence tangential
undergoes some change across the interface hence tangential  is said to be discontinuous across the boundary.
is said to be discontinuous across the boundary.
To find the normal components we need to use Gauss’s law. Consider a Gaussian surface in the form of right circular cylinder placed in such a way that half of it lies in dielectric 1 while the remaining half in dielectric 2. The height ∆h ->0 hence flux leaving from its lateral surface is zero. The surface area of its top and bottom is ∆S.
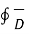 . d
. d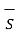 = Q
= Q
[ 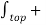
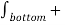
 . d
. d = Q
= Q
But 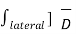 . d
. d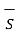 =0 as ∆h ->0
=0 as ∆h ->0
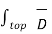 . d
. d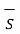 +
+  . d
. d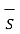 = Q
= Q
The flux leaving normal to the boundary to the top and bottom surfaces.
|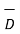 | = DN1 for dielectric 1 and DN2 for dielectric 2.
| = DN1 for dielectric 1 and DN2 for dielectric 2.
As top and bottom surfaces are elementary flux density can be assumed constant and can be taken out of integration
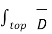 . d
. d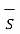 = DN1
= DN1  . d
. d = DN1 ∆ S
= DN1 ∆ S
For top surface the direction DN is entering the boundary while for bottom surface
|D| = DN1 for dielectric 1 and DN2 for dielectric 2
And as top and bottom surfaces are elementary flux density can be assumed constant and can be taken out of integration.
 . d
. d 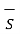 = DN1
= DN1 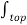 . d
. d 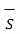 = DN1 ∆S
= DN1 ∆S
For top surface the direction of DN is entering the boundary while for bottom surface the direction of DN is leaving the boundary. Both are opposite in direction at the boundary.
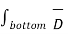 . d
. d 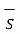 = -DN2
= -DN2 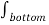 . d
. d 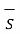 = -DN2 ∆S
= -DN2 ∆S
DN1 ∆S - DN2 ∆S = Q
But Q = 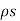 ∆S
∆S
DN1 - DN2 = = 
Consider two conducting materials M1 and M2 which are placed in a dielectric medium having permittivity 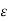 . The material M1 carries a positive charge Q while the material M2 carries a negative charge equal in magnitude as Q. There are no other charges present and the total charge of the system is zero.
. The material M1 carries a positive charge Q while the material M2 carries a negative charge equal in magnitude as Q. There are no other charges present and the total charge of the system is zero.
In conductors, charges cannot reside within the conductor and it resides only on the surface. Thus, for M1 and M2 charges +Q and -Q reside on the surfaces M1 and M2 respectively. This is shown in figure.

Capacitance
Such a system which has two conducting surfaces carrying equal and opposite charges separated by a dielectric is called capacitive system giving rise to capacitance.
The electric field is normal to the conductor surface and the electric flux is directed from M1 and M2 in such a system. There exists a potential difference between the two surfaces of M1 and M2. Let this potential be V12. The ratio of magnitudes of the total charge on any one of the two conductors and the potential difference between the conductors is called capacitance of the two-conductor system denoted as C.
C = Q/ V12
In general C =Q/V
Where Q = charge in coulombs
V = Potential difference in volts.
The capacitance is measured in farads.
Consider the three capacitors in series connected across the applied voltage V as shown in figure.
Suppose this pushes charge Q on C1 then the opposite plate of C1 must have the same charge. This charge which is negative must have been obtained from the connecting leads by the charge separation which means that the charge on the upper plate of C2 is also Q . In short all the three capacitors have the same charge Q.
Q = C1 V1 = C2 V2 = C3 V3
V1 = Q/C1 ; V2 = Q/C2 ; V3 = Q/C3
If an equivalent capacitor stores the same charge when applied with same voltage
Ceq = Q/V or V = Q/Ceq
But V = V1 + V2 + V3
Q/Ceq = Q/C1 + Q/C2 + Q/C3
1/Ceq = 1/C1 + 1/C2 + 1/C3
For n capacitors in series
1/Ceq = 1/C1 + 1/C2 +……………….+ 1/Cn.
From the Gauss’s law in the point form Poisson’s equation can be derived. Consider the Gauss’s law in the point form as
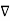 .
. 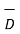 =
= 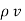
 = flux density
= flux density
 Volume charge density.
Volume charge density.
For a homogeneous isotropic and linear medium, flux density and the electric field are directly proportional. Thus,
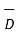 =
= 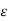 .
. 
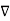 .
. 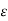 .
. 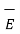 =
= 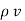
From the gradient relationship
E = - 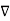 . V
. V
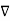 .
. 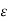 (-
(-  . V) =
. V) = 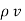
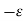 (
( 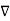 .
.  V) =
V) = 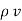
 .
.  V) =-
V) =- 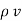 /
/ 
Now 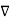 .
. 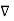 operation is called ‘del squared’ operation denoted as
operation is called ‘del squared’ operation denoted as  2.
2.
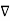 2. V = -
2. V = - 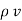 /
/ 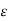
This equation is called as Poisson’s Equation
If in a certain region volume charge density is zero (  which is true for dielectric medium then the Poisson’s equation takes the form,
which is true for dielectric medium then the Poisson’s equation takes the form,
 2. V =0.
2. V =0.
This equation is called Laplace’s equation.
The procedure to solve a problem involving Laplace’s equation is :
Step 1: Solve the Laplace equation using the method of integration. Assume constants of integration.
Step2. Determine the constants by applying the boundary conditions given or known for the region. The solution obtained in step1 with constants obtained using boundary conditions is an unique solution.
Step 3: Then 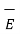 can be obtained for the potential field V obtained using gradient operation -
can be obtained for the potential field V obtained using gradient operation -  V.
V.
Step 4. For homogeneous medium 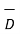 can be obtained as
can be obtained as 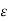
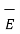 .
.
Step 5: At the surface  = DN hence
= DN hence 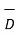 is known. The normal component DN to the surface is known. Hence the charged induced on the conductor surface can be obtained as
is known. The normal component DN to the surface is known. Hence the charged induced on the conductor surface can be obtained as
Q = -  dS
dS
Step 6: Once the charged induced Q is known and potential V is known then the capacitance C of the system can be obtained.
If 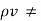 0 then the same procedure can be obtained to solve Poisson’s equation.
0 then the same procedure can be obtained to solve Poisson’s equation.
Using Laplace or Poisson’s equation we obtain:
- Potential at any point in between two surfaces when potential at two surface are given.
- We can also obtain capacitance between these two surfaces.
References:
- Faraday, Maxwell, and the Electromagnetic Field:by Basil Mahon and Nancy Forbes.
- ELECTROMAGNETISM: Theory and Applications Book by ASHUTOSH PRAMANIK
- Field and wave electromagnetics Textbook by David K. Cheng