Unit 7
Electromagnetic Waves
Maxwell’s equations in empty space (free of charges and currents) are :
Gauss’s Law for electricity 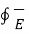 . d
. d  =0
=0
Gauss’s Law for magnetism 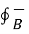 . d
. d  =0
=0
Faraday’s law of induction 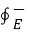 . d
. d 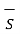 = d ɸB/dt
= d ɸB/dt
Ampere’s law  . d
. d  = μo
= μo dɸꙴ / dt
dɸꙴ / dt
According to Faraday’s Law changing magnetic fields make electric fields and according to Ampere’s law changing electric fields make magnetic fields . This is the essence of the propagation of electromagnetic waves. The fields produce each other as they change in space and time.
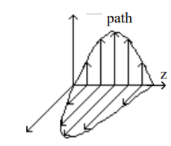
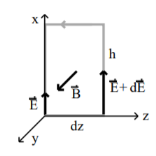


Consider a rectangular path in the x-z plane of height h and width dz as shown.
Apply Faraday’s Law  . d
. d  = d ɸB/dt
= d ɸB/dt  . d
. d 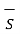 = -d/dt
= -d/dt 
The path integral only has contributions along vertical portions of the path
 . d
. d 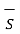 = (E + dE) h – Eh = hdE
= (E + dE) h – Eh = hdE
The flux integral can be done because the B-field is nearly constant over the rectangle.
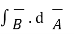 = Bhdz
= Bhdz
Putting these results in Faraday’s law hdE = -d/dt (Bhdz)
The only thing changing with time is the B-field so , dE = -dz . DB/dt = -dB/dt .
If this were done with total mathematical rigor the derivatives are actually partial derivatives.
So the relationship between E and B form Faraday’s Law is
∂E/ ∂z = ∂ B / ∂t
Now consider a rectangular path in the y-z plane of length l and width dz as shown. Apply Ampere’s law
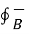 . d
. d  = μo
= μo  d/dt
d/dt 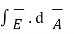
The path integral only has contributions along portions parallel to the y-axis
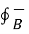 . d
. d 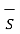 = B l – (B+ dB ) l = -l dB
= B l – (B+ dB ) l = -l dB
The flux integral can be done because the E-field is nearly constant over the rectangle
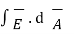 = El dz
= El dz
Putting these results into Ampere’s Law ,
-l dB = = μo  d/dt (Eldz) - dB/dz = μo
d/dt (Eldz) - dB/dz = μo 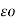 dE/dt . Because only the E-field is changing with time. Again these are actually partial derivatives. So the relationship E and B from Ampere’s law is ∂ B / ∂ z = - μo
dE/dt . Because only the E-field is changing with time. Again these are actually partial derivatives. So the relationship E and B from Ampere’s law is ∂ B / ∂ z = - μo  ∂ E/∂ t .
∂ E/∂ t .
In summary
∂ E / ∂ z = - 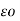 ∂ E/∂ t
∂ E/∂ t
Is ∂ B / ∂ z = - μo 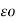 ∂ E/∂ t .
∂ E/∂ t .
Taking the derivative with respect to z of the first equation and the derivative with respect to the second equation gives
∂ 2 E / ∂ z 2 = - ∂ B / ∂ z ∂ t and ∂ 2 B / ∂ z ∂t = - μo 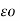 ∂ 2 E/∂ t 2
∂ 2 E/∂ t 2
Combining the results produces ∂ 2 E / ∂ z 2 = μo  ∂ 2 E/∂ t 2
∂ 2 E/∂ t 2
This is called Wave Equation.
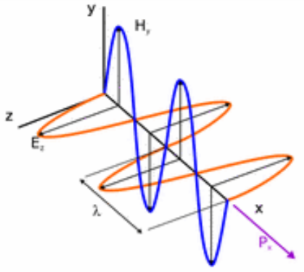
Waves with constant phase fronts whose amplitude (Eo) is uniform.
 x
x  = -jwμo H
= -jwμo H
Where E field of a uniform plane is given by
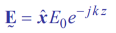
The magnetic field is then
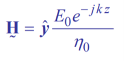
E field is in 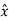 direction
direction
H field is in  direction
direction
Wave is propagating in 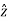 direction
direction
Or in time-domain
E(z,t) = Re { E e jwt }  =
= 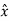 Eo cos (wt – kz)
Eo cos (wt – kz)
Similarly
H(z,t) = Re { E e jwt / 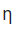 o }
o }  =
= 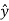 Eo /
Eo /  o cos (wt -kz)
o cos (wt -kz)
Maxwell’s equations is considered for time-harmonic fields. These fields whose only time dependence is sinusoidal which may be represented in phasor domain just like scalar time-harmonic functions.
For example, we write the relationship between time-harmonic field 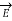 (
( , t) and its phasor field
, t) and its phasor field  (
( as
as
 (
( , t) = Real {
, t) = Real { 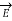 (
(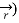 exp(j2
exp(j2 )}
)}
Where f is the frequency of radiation. The phasor representation simplifies the analysis of electromagnetic waves since it completes removes the time dependency from all field components.

Maxwell’s equations in phasor form
It is possible to express any wave as a superposition of harmonics with different frequencies. Then for each harmonic the wave equation
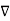 2
2 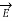 -
- 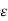 μ ∂ 2
μ ∂ 2 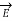 / ∂ t 2 = 0
/ ∂ t 2 = 0
Can be written in the form of equation for the phasor
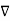 2
2 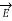 + w 2
+ w 2 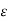 μ
μ 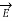 = 0 – Helmholtz equation
= 0 – Helmholtz equation
We omitted here the underline symbol in the phasor 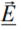 that represents the sinusoidal function of time
that represents the sinusoidal function of time 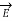 (
( , t) . Solution for every component of the phasor
, t) . Solution for every component of the phasor  can be obtained by using the procedure of separation of variables.
can be obtained by using the procedure of separation of variables.
In rectangular (Cartesian) coordinates
Ei(x,y,z) = Xi (x) Yi(y) Zi(z) (i=x,y,z)
From Helmholtz equation we obtain
∂ 2 Xi / ∂ x 2 . 1/(Xi(x)) + ∂ 2 Yi / ∂ y 2 . 1/(Yi(y)) + ∂ 2 Zi / ∂ z 2 . 1/(Zi(z) + w 2 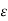 μ =0
μ =0
It follows that each of the first three terms must be constant
∂ 2 Xi / ∂ x 2 . 1/ 1/(Xi(x))= -k 2 x ( k 2 x = constant >0)
∂ 2 Yi / ∂ y 2 . 1/(Yi(y)) = -k 2 y ( k 2 y = constant >0)
∂ 2 Zi / ∂ y 2 . 1/(Zi(z)) = -k 2 z ( k 2 z = constant >0)
Where k 2 x, k 2 y, k 2 z satisfy the so-called dispersion equation.
k 2 = k 2 x+ k 2 y+ k 2 z = w 2 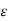 μ
μ
Xi(x) = Ai e -ikx + Bi eikx
If only first term is retained in phasor the sinusoidal in time domain solution for the field will have the form
Xi(x,t) = Re { Ai e –i(kx-wt)} = Ai cos(kx -wt)
It corresponds to the wave travelling in positive x-direction.
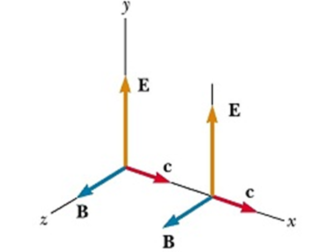
 . d S = μo ꙴ o dɸ E / dt
. d S = μo ꙴ o dɸ E / dt
In empty space where Q=0 and I=0
The following are the differential equations relating E and B . The subscripts on the components Ey and Bz
∂ E / ∂ x = - ∂ B / ∂ t
∂ B / ∂ x = - μo 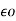 ∂E/dt
∂E/dt
For example when we evaluate ∂ E/ ∂ x we assume that t is constant . Likewise when we evaluate ∂ B / ∂ t x is held constant
∂ 2 E/ ∂ x 2 = ∂/∂x (∂B/∂t) = - ∂/∂t(∂B/∂x) = - ∂/∂t(-μoꙴ o ∂E/∂t)
∂ 2 E/ ∂ x 2 = μoꙴ o ∂ 2E/∂t 2
∂2B/∂x 2 = μoꙴ o ∂ 2B/∂t 2
The wave speed v replaced by c where
c = 1/  ꙴ o
ꙴ o
A so-called Ohmic conductor is a medium that satisfies Ohm's law, which can be written in the form
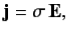 | (1) |
Where 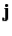 is the current density (i.e., the current per unit area),
is the current density (i.e., the current per unit area), 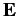 the electric field-strength, and
the electric field-strength, and 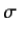 a constant known as the electrical conductivity of the medium in question.
a constant known as the electrical conductivity of the medium in question.
The 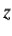 -directed propagation of a plane electromagnetic wave, linearly polarized in the
-directed propagation of a plane electromagnetic wave, linearly polarized in the  -direction, through an Ohmic conductor of conductivity
-direction, through an Ohmic conductor of conductivity 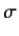 is governed by
is governed by
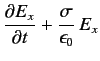 | 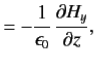 | (2) |
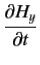 | 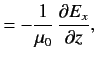 | (3) |
For a so-called good conductor, which satisfies the inequality 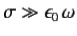 , the first term on the left-hand side of Equation (3) is negligible with respect to the second term, and the previous two equations reduce to
, the first term on the left-hand side of Equation (3) is negligible with respect to the second term, and the previous two equations reduce to
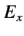 | 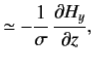 | (4) |
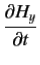 | 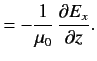 | (5) |
These equations can be solved to give
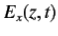 | 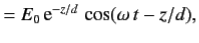 | (6) |
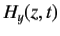 | 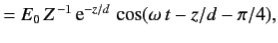 | (7) |
Where
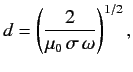 | (8) |
And
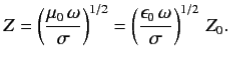 | (9) |
Equations (7) and (9) indicate that the amplitude of an electromagnetic wave propagating through a conductor decays exponentially on a characteristic length scale, 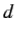 , that is known as the skin-depth.
, that is known as the skin-depth.
Consequently, an electromagnetic wave cannot penetrate more than a few skin-depths into a conducting medium.
The skin-depth is smaller at higher frequencies. This implies that high frequency waves penetrate a shorter distance into a conductor than low frequency waves.
A dielectric material can be lossy that is exhibit a nonzero conductivity 
In this situation a conduction current must be added to the displacement current when considering Ampere’s law.
 x E (r) = -jw μ H ( r )
x E (r) = -jw μ H ( r )
 x H (r) = j ( r ) + j w
x H (r) = j ( r ) + j w  E(r) = (
E(r) = ( 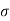 + j w
+ j w 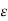 ) E( r )
) E( r )
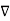 2 E (r ) – j w μ (
2 E (r ) – j w μ ( 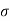 + j w
+ j w 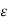 ) E (r ) =0
) E (r ) =0
Assuming as previously that the electric field is linearly polarized in the y direction and the wave propagates in the z direction
Where the propagation constant
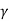 2 = j w μ (
2 = j w μ ( 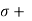 j w
j w  ) = (jw) 2 μ
) = (jw) 2 μ  ( 1 +
( 1 + 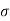 / j w
/ j w 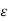 )
)
The propagation constant is complex
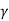 = α + j β
= α + j β
In a vacuum α = 0 and β = k. In general case the real and imaginary parts are non- linear functions of the frequency
α (w) = 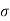

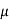 / 2
/ 2 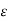 [ 1 + 1 + (
[ 1 + 1 + (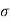 / w
/ w 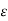 ) 2
) 2
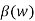 = w
= w 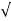

 2[ 1 +
2[ 1 + 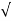 1 + (
1 + (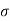 / w
/ w 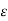 ) 2
) 2
As a result the phase velocity may depend on the waves frequency. This phenoma is called dispersion and the medium in which wave is propagating called a dispersive medium.
Consider the propagation of an electromagnetic wave through a conducting medium which obeys Ohm's law:
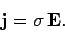 | (1) |
Here, 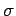 is the conductivity of the medium in question. Maxwell's equations for the wave take the form:
is the conductivity of the medium in question. Maxwell's equations for the wave take the form:
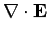 | 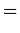 | 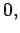 | (2) |
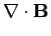 | 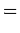 | 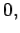 | (3) |
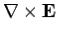 | 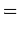 | 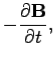 | (4) |
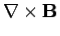 | 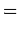 | 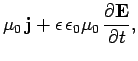 | (5) |
Where 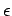 is the dielectric constant of the medium. It follows, from the above equations, that
is the dielectric constant of the medium. It follows, from the above equations, that
![\begin{displaymath}
\nabla\times\nabla\times{\bf E} = -\nabla^2{\bf E} = -\frac{...
... \epsilon_0\mu_0 \frac{\partial {\bf E}}{\partial t}\right].
\end{displaymath}](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1649483988_5335429.png) | (6) |
Looking for a wave-like solution of the form
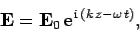 | (7) |
We obtain the dispersion relation
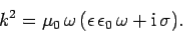 | (8) |
Consider a poor'' conductor for which 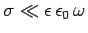 . In this limit, the dispersion relation (8) yields
. In this limit, the dispersion relation (8) yields
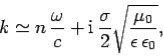 | (9) |
Where 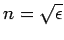 is the refractive index. Substitution into Eq. (8) gives
is the refractive index. Substitution into Eq. (8) gives
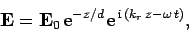 | (10) |
Where
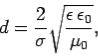 | (11) |
And 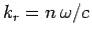 . Thus, we conclude that the amplitude of an electromagnetic wave propagating through a conductor decays exponentially on some length-scale,
. Thus, we conclude that the amplitude of an electromagnetic wave propagating through a conductor decays exponentially on some length-scale, 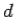 , which is termed the skin-depth.
, which is termed the skin-depth.
Note, from Eq. (11), that the skin-depth for a poor conductor is independent of the frequency of the wave.
Note, also, that 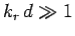 for a poor conductor, indicating that the wave penetrates many wave-lengths into the conductor before decaying away.
for a poor conductor, indicating that the wave penetrates many wave-lengths into the conductor before decaying away.
Consider a good'' conductor for which 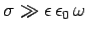 . In this limit, the dispersion relation (11) yields
. In this limit, the dispersion relation (11) yields
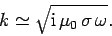 | (12) |
Substitution we get
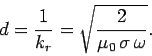 | (13) |
It can be seen that the skin-depth for a good conductor decreases with increasing wave frequency. The fact that 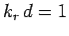 indicates that the wave only penetrates a few wave-lengths into the conductor before decaying away.
indicates that the wave only penetrates a few wave-lengths into the conductor before decaying away.
We derived the equation
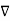 2 E = μ ꙴ ∂ 2 E /
2 E = μ ꙴ ∂ 2 E / 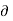 t2 + μ
t2 + μ 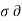 E /
E /  t ------------------------(1)
t ------------------------(1)
Where σ is the conductivity.
Substituting a plane wave
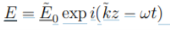 ---------------------------------------(2)
---------------------------------------(2)
Yields
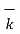 2 =
2 = 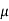
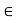 w 2 + I μ
w 2 + I μ  w --------------------------------------------(3)
w --------------------------------------------(3)
To solve this we have to take a complex wavenumber
˜k = k + iκ-------------------------------------------------------------- (4)
Equating the real and imaginary parts in (3) yields
k 2 − κ 2 = 
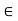 w 2 ---------------------------------------------------------- (5)
w 2 ---------------------------------------------------------- (5)
2kκ = µσω -----------------------------------------------------------------------------------. (6)
The second equation can be solved for κ = µσω /2k then eliminating κ from (5) yields
k 4 – (µσω /2) 2 = µσω 2 k 2
This is a quadratic in k 2 with solution
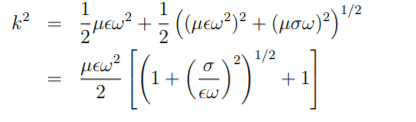
Then we can use (5) to obtain

Now the complex wavenumber (4) implies
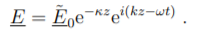
The first exponential decays with z and causes attenuation of the wave.
The characteristic distance over which the wave decays is known as the skin depth and is given by
δ = 1/k
Thus, the skin depth is the typical distance a wave penetrates into a conductor.
Poynting theorem states that the net power flowing out of a given volume V is equal to the time rate of decrease of stored electromagnetic energy in that volume decreased by the conduction losses is the total power leaving the volume = rate of decrease of stored electromagnetic energy ohmic power dissipated due to motion of charge.
Proof:
The energy density carried by the electromagnetic wave can be calculated using Maxwell's equations
Div  = 0 -----------------------------(i)
= 0 -----------------------------(i)
Div 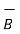 = 0 ---------------------------------(ii)
= 0 ---------------------------------(ii)
Curl  = - ∂ B / ∂t -----------------------------------(iii)
= - ∂ B / ∂t -----------------------------------(iii)
And curl 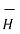 =
= 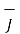 + ∂
+ ∂  / ∂t
/ ∂t
Taking scalar product of (iii) with H and (iv) with 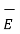
That is 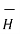 curl
curl 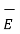 = -
= - 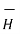 . ∂
. ∂ 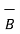 / ∂t --------------------------------------(iv)
/ ∂t --------------------------------------(iv)
 curl
curl 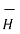 =
= 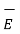 .
. 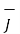 +
+ 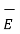 . ∂
. ∂ 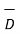 / ∂t ----------------------------------------(v)
/ ∂t ----------------------------------------(v)
So div ( x
x 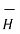 ) = - [
) = - [ 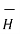 ∂
∂ 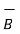 / ∂ t +
/ ∂ t + 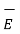 ∂
∂ 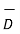 / ∂ t] -
/ ∂ t] - 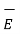 .
. 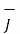
But 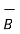 = μ
= μ 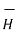 and
and  =
= 
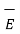
So 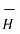 ∂
∂ 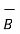 / ∂ t =
/ ∂ t = 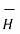 ∂
∂ 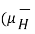 )/ ∂ t = ½ μ ∂/∂t (H 2)
)/ ∂ t = ½ μ ∂/∂t (H 2)
= ∂/∂t [ ½ 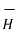 .
.  ]
]
And 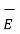 ∂
∂  / ∂ t =
/ ∂ t = 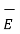 ∂ / ∂ t ( μ
∂ / ∂ t ( μ 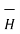 ) = ½ μ ∂ / ∂ t (H 2 )
) = ½ μ ∂ / ∂ t (H 2 )
= ∂ / ∂ t (1/2 . .
. 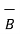 )
)
And 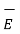 ∂
∂  / ∂ t =
/ ∂ t =  ∂ / ∂ t (
∂ / ∂ t ( 
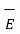 ) = ½
) = ½ 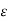 ∂ / ∂ t (E 2 ) = ∂ / ∂ t [ ½
∂ / ∂ t (E 2 ) = ∂ / ∂ t [ ½ 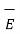 .
.  ]
]
So from equation div ( 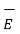 x
x  ) = - ∂ / ∂ t [ ½
) = - ∂ / ∂ t [ ½  .
. 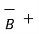
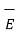 .
.  ] -
] - 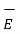 .
. 
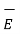 .
.  = - ∂ / ∂ t [ ½
= - ∂ / ∂ t [ ½ 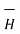 .
. 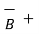
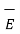 .
. 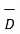 ] – div (
] – div (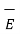 x
x 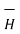 )
)
Integrating equation over a volume V enclosed by a surface S
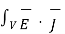 dV = - |∂ / ∂ t [ ½
dV = - |∂ / ∂ t [ ½ 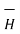 .
. 
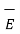 .
.  | dV -
| dV -  ((
((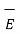 x
x  ) dV
) dV
Or 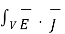 dV = -
dV = - 
 H 2 + ½
H 2 + ½  E 2 ] dV -
E 2 ] dV - 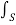 ((
(( x
x  ) ds
) ds
As  = μ
= μ 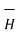
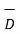 =
= 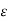
 and
and 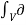 Ucm / ∂t dV -
Ucm / ∂t dV -  x
x 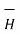 .ds
.ds
Or - 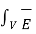 x
x  .dV = - ∂/∂t
.dV = - ∂/∂t 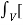 ½[ μ H 2 + ½
½[ μ H 2 + ½  E 2] dV -
E 2] dV - 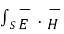 ds
ds
Or 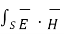 ds = -
ds = -  Ucm / ∂t dV -
Ucm / ∂t dV - 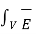 x
x 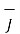 .dV
.dV
Or 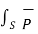 ds = - -
ds = - -  Ucm / ∂t dV -
Ucm / ∂t dV - 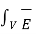 x
x  .dV
.dV
That is the Total power leaving the volume = rate of decrease of stored e.m.f energy - ohmic power dissipated due to charge motion
This equation represents the poynting theorem according to which the net power flowing out of a given volume is equal to the rate of decrease of stored electromagnetic energy in that volume minus the conduction losses.
References:
- Faraday, Maxwell, and the Electromagnetic Field:by Basil Mahon and Nancy Forbes.
- ELECTROMAGNETISM: Theory and Applications Book by ASHUTOSH PRAMANIK
- Field and wave electromagnetics Textbook by David K. Cheng