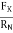UNIT 9
FRICTION
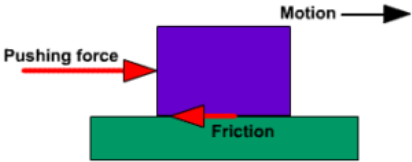
‘Friction‘is a force that resists motion of sliding or rolling of one object moving relative to another. It is a result of the electromagnetic attraction between the charged particles of two touching surfaces. We find and use it everywhere and every day whenever objects come into contact with each other. Although it always acts in the always acts in the direction opposite to the way an object wants to slide.
For example, we use car brakes if we want to stop or slow down because of the friction created between the brakes and wheels that slow/stop the car down.
Or the Friction is also define as the force that resists motion when the surface of one object comes in contact with the surface of another. The mechanical advantage of a machine is reduced by friction, or in other words, the ratio of output to input is reduced because of friction. An automobile uses one-quarter of its energy on limiting the friction. Yet, it is also friction in the tires that allows the car to stay on the road and friction in the clutch that makes it possible to drive. From matches to machines to molecular structures, friction is one of the most significant phenomena in the physical world.
Frictional force refers to the force generated by two surfaces that contacts and slide against each other.
A few factors affecting the frictional force:
- These forces are mainly affected by the surface texture and amount of force impelling them together.
- The angle and position of the object affect the amount of frictional force.
- If an object is placed flat against an object, then the frictional force will be equal to the weight of the object.
- If an object is pushed against the surface, then the frictional force will be increased and becomes more than the weight of the object.
Calculating the Force of Friction
The maximum amount of friction force that a surface can apply upon an object can be easily calculated with the use of the given formula:
Ffriction = µ • Fnormal
Find the Normal Force
The normal force is the support force exerted upon an object that is in contact with another stable object. The normal force can be simply described in most cases by the following formula:
N = mg
In this formula, m describes the mass of the object, and g stands for the acceleration due to gravity. In case of an inclined surface, the strength of the normal surface is reduced the more the surface is inclined, hence the formula becomes:
N = mg cos(θ)
θ represents the angle the surface is inclined to. In a simple calculation, you would calculate the normal force of a 2-kg block of wood sitting on a surface as4 N = 2 kg × 9.8 N/kg = 19.6 N
Finding the Right Co-efficient
The co-efficient that you would choose depends on the object and the specific situation. If the object isn’t moving across the surface, you use the coefficient of static friction μ static, but if the object under consideration is moving you use the coefficient of sliding friction μ slide. The type of materials used also affects the co-efficient. For example, if a block wood was on a brick surface, the coefficient would be 0.6, but if it were on a block of clean wood, it would range from 0.25 to 0.5.
Calculating Frictional Force
As discussed, the formula for frictional force is given by F = μN.
As an example, let us consider the block of wood that weighs 2-kg resting on a table to be pushed from rest. In this case, we consider the static friction co-efficient. 0.5 is the static co-efficient of wood.
With the given details, we can calculate the normal force as N = 2 kg × 9.8 N/kg = 19.6 N Now that we have the values of normal force and static friction co-efficient, we can calculate the frictional force as follows
F = 0.5 × 19.6 N = 9.8 N
Are there Different Types of Frictional Force
Yes, there are different types of frictional forces. The friction that takes place between solid surfaces is classified as Static, Kinetic, Rolling, and Sliding Friction. The friction that takes place between fluids and gases are termed as fluid friction. Hence, friction is broadly classified as:
- Dry Friction
- Static Friction
- Kinetic Friction
- Rolling Friction
- Sliding Friction
- Fluid Friction
Dry Friction
Dry friction describes the reaction between two solid bodies in contact when they are in motion (kinetic friction) and when they are not (static friction). Both static and kinetic friction is proportional to the normal force exerted between the solid bodies. The interaction of different substances is modelled with different coefficients of friction. By this, we mean that certain substances have a higher resistance to movement than others for the same normal force between them.
1) Static Friction
Static friction is a force that keeps an object at rest.
The friction experienced when individuals try to move a stationary object on a surface, without actually triggering any relative motion between the body and the surface which it is on.
It can be explained as the force of friction which precisely balances the applied force for the duration of the stationary state of the body. The static frictional force is a self-regulating force, i.e. static friction will at all times be equivalent and opposite to the force applied. R is the reaction force because of the weight W. the external force is F and fr is the friction. F = -fr when no motion takes place.

Static Friction Examples
Some real-life examples of static friction are given in the points below.
- Papers on a table top
- A towel hanging on a rack
- A bookmark in a book
- A car parked on a hill
Laws of Static Friction
- The maximum force of static friction is not dependent on the area of contact.
- The maximum force of static friction is comparative to the normal force i.e., if the normal force increases, the maximum external force that the object can endure without moving, also increases.
Limiting Friction:
It is the highest value of static friction which comes into play when an object is just about to slide over the surface of a different object. For an exerted external force greater than the limiting friction, the body begins to move.
Once the motion has started, static friction cannot be considered. A new type of friction termed as kinetic friction comes into play.
Laws of Limiting Friction:
- The direction of limiting frictional force is always contrary to the direction of motion.
- Limiting friction acts tangentially to the two surfaces interacting.
- The magnitude of limiting friction is proportional to the normal reaction amidst the two surfaces.
- The limiting friction hinges upon the material, the nature of the surfaces interacting, and their evenness.
- So long as the normal reaction is the same, the magnitude of limiting friction is free of the shape or the area of the surfaces in contact, for any two given surfaces.
2) Kinetic Friction
Kinetic friction is defined as a force that acts between moving surfaces. A body moving on the surface experiences a force in the opposite direction of its movement. The magnitude of the force will depend on the coefficient of kinetic friction between the two materials.
Friction is easily defined as the force that holds back a sliding object. The kinetic friction is a part of everything and it interferes motion of two or more objects. The force acts in the opposite direction to the way an object wants to slide. If a car has to stop, we apply brakes and that is exactly where the friction comes into play. While walking, when one wants to suddenly come to a halt, friction is to thank again. But when we have to stop in the middle of a puddle, things get harder since friction is less there and cannot aid one so much.

A Model For Kinetic Friction
Kinetic Friction Formula
The coefficient of kinetic friction is denoted by the Greek letter “mu” (μ), with a subscript “k”. The force of kinetic friction is μk times the normal force on a body. It is expressed in Newton’s (N). The kinetic friction equation can be written as:
Force of kinetic friction = (coefficient of kinetic friction)(normal force)
Fk= μk η
Where,
- Fk = force of kinetic friction
- μk = coefficient of kinetic friction
- η = normal force (Greek letter “eta”)
Types of Friction
There are two main types of friction which are mentioned in the points below.
- Static Friction
- Kinetic Friction.
Static friction is the one present between two objects that are not moving with respect to each other. In liquids, friction is the resistance between moving layers of a fluid better known as viscosity. Now take two moving solid objects, this is known as moving or kinetic friction due to its motion.
This friction is a particular fraction of the perpendicular force acting between two bodies. A coefficient of friction determines the fraction which in turns determined through experiments. The force is independent of the contact area and doesn’t change no matter how fast the two objects are moving. While in contrast, static friction is what affects stationary objects. The force of friction is a force that resists motion when two objects are in contact. If you look at the surfaces of all objects, there are tiny bumps and ridges. Those microscopic peaks and valleys catch on one another when two objects are moving past each other. There are of course other forces at work like chemical bonding and electrical interactions.
Applications of Kinetic Friction
- Friction also plays a huge role in everyday occurrences like while rubbing of two objects takes place. The resulting motion converts into heat and thus resulting in the fire in some instances.
- It is also responsible for wear and tear and that’s why we need oil to lubricate machine parts, as it reduces friction.
- When two objects are rubbed against each other, the frictional force is converted into thermal energy, in few cases giving rise to fire
- Kinetic friction is responsible for the wear and tear of machine parts, hence it is important to lubricate the machine parts with oil.
3)Rolling Friction
For a moving solid body, there are two principal types of friction that act upon it:
- The force resisting the motion of a rolling body on a surface is known as rolling friction or rolling resistance. Rolling of ball or wheel on the ground is an example of Rolling friction.
- The other type of friction is sliding friction. In this type of friction, there is a restriction on the body’s movement as only one side of the body is in contact with the surface. Pushing a box across the table is an example of Sliding friction.
Rolling friction is considerably weaker than sliding friction.
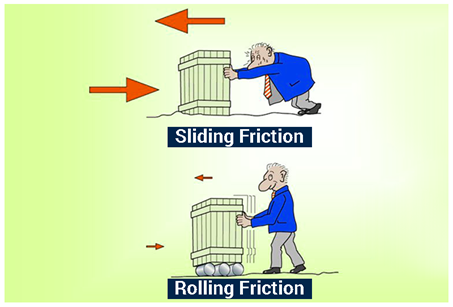
Laws of Rolling Friction
There are three laws of rolling friction:
- With the increase in smoothness, the force of rolling friction decreases.
- Rolling friction is expressed as a product of load and constant to the fractional power.
F = kLn
- Rolling friction force is directly proportional to load and inversely proportional to the radius of curvature.
F=μ×Wr
Cause of Rolling Friction
When an object is rolled on a surface, certain things happen:
- The object is deformed at the point of contact with the surface.
- The surface is deformed at the point of contact with the object.
- The motion is created below the surface as a result of the above-mentioned points.
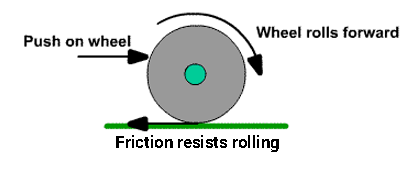
The primary cause of this friction is that the energy of deformation is greater than the energy of recovery. Also, there is an adhesive force between the two surfaces which needs to be overcome constantly. The amount of friction is based on a variety of factors such as:
- The quality of the sliding body
- The quality of the surface
- Load
- The diameter of the rolling object
- The surface area of the body
Coefficient of Rolling Friction
Determining the coefficient of this friction is considerably more complex than that of sliding friction.
“Coefficient of Rolling Friction is the ratio of the force of rolling friction to the total weight of the object.”
In empirical terms, the coefficient of rolling resistance can be expressed as:
Fr=μrW
Where,
- Fr is the resistive force of rolling resistance
- μr is the coefficient of rolling resistance
- W is the weight of the rolling body
Rolling Friction Examples
- A basketball rolled on the court will eventually come to a halt because of rolling friction.
- A bike with a broad tire will burn more fuel because of the increased rolling friction.
- A ball rolled on a field will go lesser distance than a ball rolling on a concrete floor because it will experience greater rolling friction on the former surface.
4) Sliding Friction
We can define sliding friction as the resistance created by any two objects when sliding against each other. This friction is also known as kinetic friction and is defined as the force that is needed to keep a surface sliding along another surface. It depends on two variables- one is material and the other is the weight of the object. Any change in the surface area in contact does not change the sliding friction. In most of the materials, sliding friction is less than static friction. There are exceptions that include metals having static and sliding friction coefficients and are essentially the same with small surfaces where molecular attraction forces take over.
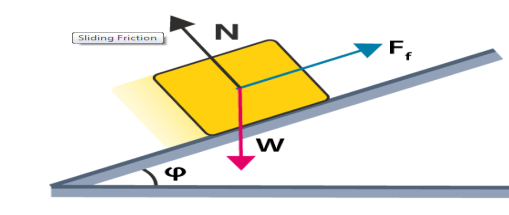
Sliding Friction Formula
The equation for sliding force includes the coefficient of sliding friction times the normal force.
FS = μSFn
Where,
FS = force of sliding friction
μS = Coefficient of sliding friction
Fn = normal force
Factors affecting sliding friction
- The surface deformation of objects.
- The roughness or smoothness of the surface of the objects.
- The original speed of either object.
- The size of the object.
- Finally, the amount of pressure on either object.
Examples of Sliding Friction
- Rubbing both the hands together to create heat.
- A child sliding down through a slide in a park.
- A coaster sliding against a table.
- A washing machine pushed along with the floor.
- The frame and the edge of the door sliding against one another.
- A block being slid across the floor.
- Two cards in a deck sliding against each other.
Sliding can occur between two objects of arbitrary shape whereas the rolling friction is the frictional force that is associated with the rotational movement. The rolling friction is usually less than the one associated with sliding kinetic friction. The values for the coefficient of rolling friction are quite less than that of sliding friction. It usually produces greater sound and thermal bi-products. For example- Movement of braking motor vehicle tires on a roadway.
Fluid Friction
Fluid Friction is the force that obstructs the flow of fluid. It is a situation where the fluid provides resistance between the two surfaces. If both the surfaces offer high resistance then it is known as high viscous and, generally, we call them greasy.
Examples of Fluid Friction
- To avoid creaking sounds from doors, we lubricate the door hinges which leads to the smooth functioning of door hinges.
- When you drop the ball in a full bucket of water, water splashes out of the bucket and is all because of buoyancy of fluid.
When the two objects slide over each other the force which opposes this type of motion is called as Friction. This force always acts tangentially to the surface and its direction is opposite to that of the motion of bodies.
Laws of Coulomb’s Friction
Coulomb friction is also known as Dry friction and was named after C. A. Coulomb who extensively studied this phenomenon. Dry friction is considered to exist between the two surfaces of objects which are in contact when there is absence of any kind of fluid lubrication.
Dry friction may take place either due to adhesion between the surfaces, or roughness or contamination of surfaces taking place.
As there is loss of mechanical energy in the form of heat during the frictional process, it turns out to be non-conservative force that is path dependent.
The force of friction is always applied in a manner that opposes the movement created within the two surfaces. Any object moving on a road or any surface slows down and then eventually stops.
Dry friction is can be further classified into static friction which is between non-moving surfaces, and kinetic friction which is between moving surfaces.
The laws are discussed as:
Laws of Static Friction:
Following are the laws of static friction
1. The force of friction always act in direction which is opposite to motion of body.
2. The magnitude of force of friction is equal to the force acting on the body externally.
3. There is constant ratio between limiting frictional force and the normal reaction forces. Mathematically:
(F/R) = Constant
Where F = Limiting friction, and R = Normal reaction.
4. The force of friction does not depend on the area of contact between the two surfaces.
5. There is dependency of frictional force on roughness of the surfaces.
Laws of Kinematic or Dynamic Friction:
Following are the laws of kinetic or dynamic friction:
1. The force of friction always act such that it opposes the motion of body.
2. There is a constant ratio between kinetic motion and normal reaction. But this ratio is slightly less when it comes to limiting friction.
3. For medium speeds, the force due to friction stays constant. But it decreases somewhat when the speed increases.
e.g. 1: The uniform crate shown in Fig. Below has a mass of 20 kg. If a force P = 80 N is applied to the crate, determine if it remains in equilibrium. The coefficient of static friction is  = 0.3.
= 0.3.
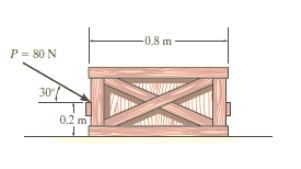
Solution:
The first step is free-body diagram i.e.
Free-Body Diagram. As shown in Fig. Diagram below, the resultant normal force NC acts at a distance of x from the centre line of crate for countering the tilting effect caused by P. Hence, there are three unknowns, F, NC and x, which can be solved by equations of equilibrium.
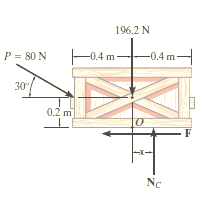
Equations of equilibrium:
Σ Fx = 0
80 cos 30° N - F = 0
Σ Fy = 0
-80 sin 30° N + NC - 196.2 N = 0
Σ M = 0
80 sin 30° N10.4 m2 - 80 cos 30° N10.2 m2 + NC (x) = 0
Thus, solving the above equations, we get,
F = 69.3 N
NC = 236 N
x = -0.00908 m = -9.08 mm
As value of x is negative, hence it acts to left of centre line of the crate. There will be no tipping since x < 0.4 m. Fmax = 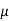 Nc = 0.3(236 N) = 70.8 N. Since F that we got is 69.3 N < 70.8 N, the crate will not slip.
Nc = 0.3(236 N) = 70.8 N. Since F that we got is 69.3 N < 70.8 N, the crate will not slip.
e.g. 2: A body of weight 300 N is lying on a rough horizontal plane having a coefficient of friction as 0.3. Determine the magnitude of the force, which is needed to move the body, acting at 25° by the horizontal.

Solution:
Given:
Weight of the body (W) = 300 N; Coefficient of friction (μ) = 0.3 and
Angle made by the force with the horizontal (α) = 25°
Let P = Magnitude of the force, which can move the body, and
F = Force of friction.
Initially, we will solve the problem in horizontal direction as,
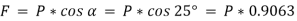
The next step is to resolve the force in vertical direction, we get,
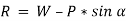
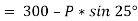
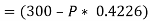
The force of friction (F) is given as,
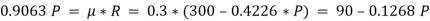
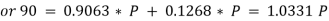
Hence, P = 87.1 N.
e.g. 3: A body, which is positioned on a rough horizontal plane, needs a pull of 180 N inclined at 30° to the plane just for moving. Also, it was found that a push of 220 N which is inclined at 30° to the plane also moved the body. Find out the weight of the body and the coefficient of friction present here.
Solution:
Given: Pull = 180 N; Push = 220 N and angle at which force is inclined with horizontal plane (α) = 30°
Let W = Weight of the body
R = Normal reaction, and
μ = Coefficient of friction.
First of all, consider a pull of 180 N acting on the body. We know that in this case, the force of friction (F1) will act towards left as shown in Fig. (a).
Resolving the forces horizontally,
F1 = 180 cos 30° = 180 × 0.866 = 155.9 N
And now resolving the forces vertically,
R1 = W – 180 sin 30° = W – 180 × 0.5 = W – 90 N
We know that the force of friction (F1),
155.9 = μR1 = μ (W – 90)
Now consider a push of 220 N acting on the body. We know that in this case, the force of friction (F2) will act towards right as shown in Fig. (b).
Resolving the forces horizontally,
F2 = 220 cos 30° = 220 × 0.866 = 190.5 N
And now resolving the forces horizontally,
R2 = W + 220 sin 30° = W + 220 × 0.5 = W + 110 N
We know that the force of friction (F2),
190.5 = μ.R2 = μ (W + 110) ...(ii)
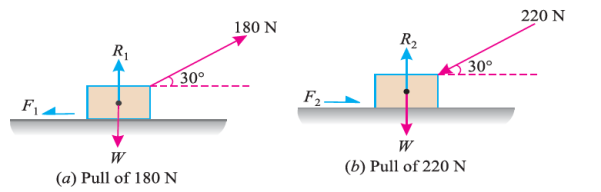
Dividing equation (i) by (ii)
155.9 W + 17 149 = 190.5 W – 17 145
34.6 W = 34 294
W = 991.2 N
Now substituting the value of W in equation (i),
155.9 = μ (991.2 – 90) = 901.2 μ
μ = 0.173
In this way, numerical based on dry friction can be solved.
Angle of repose is defines as the angle of an inclined plane, at which a body placed on it just begins to slide.
Place a body of mass m on an inclined plane. Increase the angle of inclined plane till the body just begins to slide. If θ is the angle of inclination at which the body just begins to slide, then θ is the angle of repose.

The weight mg of the body acts vertically downwards. Because of the angle of inclination, this weight can be resolved into two components; mgcosθ and mgsinθ as shown in fig.
If the body just begins to slide, then
1. Mg.sinθ is equal to the frictional force
Mgsinθ =Fc (a)
2. Mgcosθ is equal to the normal reaction
Mgcosθ=R (b)
Dividing (a) by (b),
Mgsinθ / mgcosθ = Fc / R
Tanθ = Fc / R
Tanθ = μ (2)
Thus, coefficient of limiting friction is equal to the tangent of the angle of repose.
It is “The maximum ratio of applied force to normal force with no motion” we all know Frictional force is a force which opposes motion. If we keenly observe, once you apply force to move a body from rest, there exists a point up to which the body resist to move. To move the body the applied force should be greater to overcome this resistance. This maximum resistive force offered by the body against the applied force to continue its state of motion is called Coefficient of Static Friction.
Coefficient of Static Friction Formula
The magnitude of the frictional force depends on two factors
- How heavy is the material
- How rough is the surface
The roughness of the surface is often measured by a parameter called the Coefficient Of Static Friction. It is mathematically expressed as the ratio of applied force to the normal reaction. Given by
- Coefficient of friction :
- Coefficient of static friction (
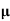 ) : from Culombs law
) : from Culombs law
 Magnitude of frictional force is directly proportional to normal reaction
Magnitude of frictional force is directly proportional to normal reaction
 FS
FS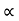 RN
RN
 FS =
FS =  S RN
S RN
 S =
S = 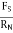
B. Coefficient of kinetic friction ( K) :
K) :
FK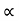 RN
RN
 FK =
FK =  K RN
K RN
 K =
K =