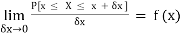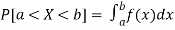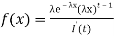Unit II

Continuous Probability Distributions

2.1           Continuous random variables and their properties

A continuous random variable is a random variable where the data can take infinitely many values. For example, a random variable measuring the time taken for something to be done is continuous since there are an infinite number of possible times that can be taken.
Continuous random variable is called by a probability density function p (x), with given properties:

p (x) ≥ 0 and the area between the x-axis & the curve is 1: ... Standard deviation of a variable Random is defined by σ x = √Variance (x).

1. A continuous random variable is known by a probability density function p(x), with these things: p(x) ≥ 0 and the area on the x-axis and the curve is 1: 

∫-∞∞ p(x) dx = 1.
 

2.     The expected value E(x) of a discrete variable is known as:
 

E(x) = Σi=1n xi pi
 

3.     The expected value E(x) of a continuous variable is called as:
 

E(x) = ∫-∞∞ x p(x) dx

4.     The Variance(x) of a random variable is known as Variance(x) = E[(x - E(x)2].
 

5.     2 random variable x and y are independent if E[xy] = E(x)E(y).
 

6.     Standard deviation of a random variable is known asσx = √Variance(x).
 

7.     Given value of standard error is used in its place of standard deviation when denoting to the sample mean.
 

σmean = σx / √n

8.     If x is a normal random variable with limitsμ and σ2 (spread = σ), mark in symbols: x ˜ N(μ, σ2).
 

9.     The sample variance of x1, x2, ..., xn is given by-

10. If x1, x2, ... , xn are explanationssince a random sample, the sample standard deviation s is known the square root of variance:

11. Sample Co-variance of x1, x2, ..., xn is known-
 

12. A random vector is a column vector of random variable. 

v = (x1 ... xn)T

13. Expected value of Random vector E(v) is known byvector of expected value of component.
If v = (x1 ... xn)T
 

E(v) = [E(x1) ... E(xn)]T

14. Co-variance of matrix Co-variance(v) of a random vector is the matrix of variances and Co-variance of component.
If v = (x1 ... xn)T, the ijth component of the Co-variance(v) is sij

Properties

Starting from properties 1 to 7, c is a constant; x and y are random variables.

1. E(x + y) = E(x) + E(y).
    
2. E(cx) = c E(y).
    
3. Variance(x) = E(x2) - E(x)2
    
4. If x and y are individual, then Variance(x + y) = Variance(x) + Variance(y).
    
5. Variance(x + c) = Variance(x)
    
6. Variance(cx) = c2 Variance(x)
    
7. Co-variance(x + c, y) = Co-variance(x, y)
    
8. Co-variance(cx, y) = c Co-variance(x, y)
    
9. Co-variance(x, y + c) = Co-variance(x, y)
    
10. Co-variance(x, cy) = c Co-variance(x, y)
     
11. If x1, x2, ...,xn are discrete and N(μ, σ2), then E(x) = μ. We say that x is neutral for μ.
     
12. If x1, x2, ... ,xn are independent and N(μ, σ2), then E(s) = σ2.   We can told S is neutral for σ2.

From given properties 8 to 12, w and v is random vector; b is a continuous vector; A is a continuous matrix.

8.     E(v + w) = E(v) + E(w)
 

9.     E(b) = b
 

10. E(Av) = A E(v)
 

11. Co-variance(v + b) = Co-variance(v)
 

12. Co-variance(Av) = A Co-variance(v) AT

Example:

Let X be a random variable with PDF given by

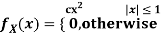
a, Find the constant c.

b. Find EX and Var (X).

c. Find P(X ).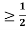

Solution.

1. To find c, we can use

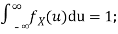
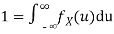
Thus we must have .

b.     To find EX we can write

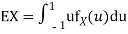
In fact, we could have guessed EX = 0 because the PDF is symmetric around x = 0. To find Var (X) we have

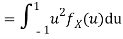
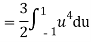
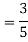
c.      To find 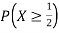we can write

Example:

Let X be a continuous random variable with PDF given by

If 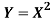, find the CDF of Y.

Solution. First we note that 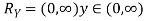, we have

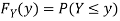
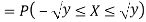
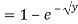
Thus,
 

Example:

Let X be a continuous random variable with PDF

Find .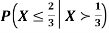

Solution. We have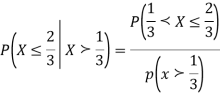
 

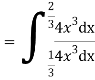
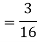
Key takeaways-

1. A continuous random variable is known by a probability density function p(x), with these things: p(x) ≥ 0 and the area on the x-axis and the curve is 1:
    
2. ∫-∞∞ p(x) dx = 1.
3. E(x) = ∫-∞∞ x p(x) dx
4. Variance(x) = E[(x - E(x)2].
5. Two random variable x and y are independent if E[xy] = E(x)E(y).
   6. Standard deviation of a random variable is known asσx = √Variance(x).

2.2           distribution functions and densities, normal, exponential and gamma densities

Probability Distribution:

A probability distribution is arithmetical function which defines completely possible values &possibilities that a random variable can take in a given range. This range will be bounded between the minimum and maximum possible values. But exactly where the possible value is possible to be plotted on the probability distribution depends on a number of influences. These factors include the distribution's mean, SD, Skewness, and kurtosis.

Discrete Probability Distribution

Suppose a discrete variate X is the outcome of some experiment. If the probability that X takes the values 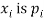, then

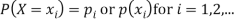
Where (i) for all values of i, (ii)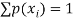

The set of values with their probabilities 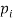constitute a discrete probability distribution of the discrete variate X.

For example the discrete probability distribution for X the sum of the numbers which turns on tossing a pair of dice is given by the following table:

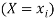	2	3	4	5	6	7	8	9	10	11	12
	1/36	2/36	3/36	4/36	5/36	6/36	5/36	4/36	3/36	2/36	1/36

Therefore there are equally likely outcomes and therefore each has the probability 1/36. We have X = 2 for one outcome i.e. (1,1): X = 3 for two outcomes (1, 2) and (2, 1): X = 4 for three outcomes (1, 3), (2, 2) and (3, 1) and so on.

Distribution function

The distribution function F (x) of the discrete variate X is defined by

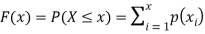where x is any integer. The graph of F (x) will be stair step form (Fig.). The distribution function is also sometimes called cumulative distribution function.

Probability Density:

Probability density function (PDF) is a arithmetical appearance which gives a probability distribution for a discrete random variable as opposite to a continuous random variable. The difference among a discrete random variable is that we check an exact value of the variable. Like, the value for the variable, a stock worth, only goes two decimal points outside the decimal (Example 32.22), while a continuous variable have an countless number of values (Example 32.22564879…).

When the PDF is graphically characterized, the area under the curve will show the interval in which the variable will decline. The total area in this interval of the graph equals the probability of a discrete random variable happening. More exactly, since the absolute prospect of a continuous random variable taking on any exact value is zero owing to the endless set of possible values existing, the value of a PDF can be used to determine the likelihood of a random variable dropping within a exact range of values.

Probability density function-

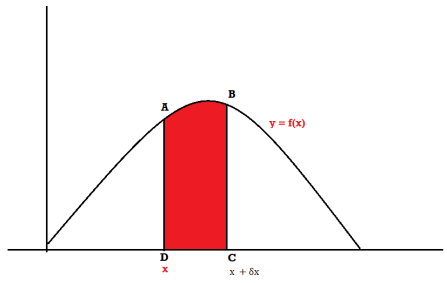
Suppose f( x ) be a continuous function of x . Suppose the shaded region ABCD shown in the following figure represents the area bounded by y = f( x ), x –axis and the ordinates at the points x and x + δx , where δx is the length of the interval ( x , x + δx ).if δx is very-very small, then the curve AB will act as a line and hence the shaded region will be a rectangle whose area will be AD × DC this area = probability that X lies in the interval ( x, x +δx )

= P[ x≤ X ≤ x +δx ]

Hence,

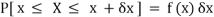
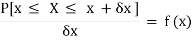
Properties of Probability density function-

1. 

2.

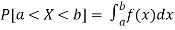
Example: If a continuous random variable X has the following probability density function:

Then find-

1. P[0.2 < X < 0.5]

Sol.

Here f(x) is the probability density function, then-

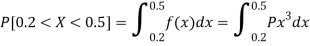
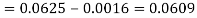
Example. The probability density function of a variable X is

(i)                Find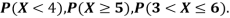

(ii)             What will be e minimum value of k so that

Solution. (i) If X is a random variable then

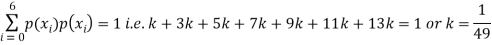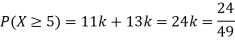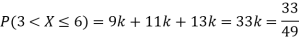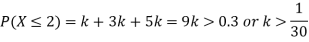
 (ii)Thus minimum value of k=1/30.

Example. A random variate X has the following probability function

x	0	1	2	3	4	5	6	7
P (x)	0	k	2k	2k	3k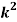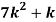

(i)                Find the value of the k.

(ii)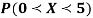            

Solution. (i) If X is a random variable then

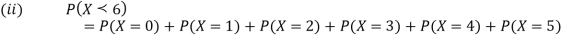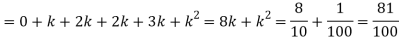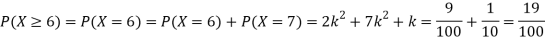
Continuous probability distribution

When a variate X takes every value in an interval it gives rise to continuous distribution of X. The distribution defined by the videos like heights or weights are continuous distributions.

a major conceptual difference however exists between discrete and continuous probabilities. When thinking in discrete terms the probability associated with an event is meaningful. With continuous events however where the number of events is infinitely large, the probability that a specific event will occur is practically zero. For this reason, continuous probability statements on must be worth did some work differently from discrete ones. Instead of finding the probability that x equals some value, we find the probability of x falling in a small interval.

Thus the probability distribution of a continuous variate x is defined by a function f (x) such that the probability of the variate x falling in the small interval 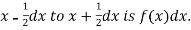Symbolically it can be expressed as Thus f (x) is called the probability density function and then continuous curve y = f(x) is called the probability of curve.

The range of the variable may be finite or infinite. But even when the range is finite, it is convenient to consider it as infinite by opposing the density function to be zero outside the given range. Thus if f (x) =(x) be the density function denoted for the variate x in the interval (a,b), then it can be written as

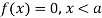
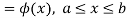
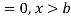
The density function f (x) is always positive and (i.e. the total area under the probability curve and the the x-axis is is unity which corresponds to the requirements that the total probability of happening of an event is unity).

(2) Distribution function

If

Then F(x) is defined as the commutative distribution function or simply the distribution function the continuous variate X. It is the probability that the value of the variate X will be ≤x. The graph of F(x) in this case is as shown in figure 26.3 (b).

The distribution function F (x) has the following properties

(i)               

(ii)             

(iii)          

(iv)            P(a ≤x ≤b)= = =F (b) – F (a).

Example.

(i)                Is the function defined as follows a density function.

(ii)             If so determine the probability that the variate having this density will fall in the interval (1.2).

(iii)          Also find the cumulative probability function F (2)?

Solution. (i) f (x) is clearly ≥0 for every x in (1,2) and

Hence the function f (x) satisfies the requirements for a density function. (ii)Required probability = This probability is equal to the shaded area in figure 26.3 (a). (iii)Cumulative probability function F(2)

Which is shown in figure

Exponential Distribution:

The exponential distribution is a C.D. Which is usually use to defineto come time till some precise event happens. Like, the amount of time until a storm or other unsafe weather event occurs follows an exponential distribution law.

The one-parameter exponential distribution of the probability density function PDF is defined:

f(x)=λ,x≥0,

Where, the rate λ signifies the normal amount of events in single time.

The mean value is μ=. The median of the exponential distribution is m=, and the variance is shown by .

Normal Distribution:

Normal distribution

Now we consider continuous distribution of fundamental importance namely the normal distribution. Any quantity whose variation depends on random causes is distributed according to the normal law. Its importance lies in the fact that a large number of distributions approximate to the normal distribution.

Latest define a variate

Where x no and S.D. so that z is a very eighth with mean zero and variance unity. In the limit as  n tends to infinity the distribution of z becomes a continuous distribution extending from .

It can be shown that the limiting form of the binomial distribution (1) for large values of n when neither p nor q is very small is the normal distribution. The normal curve is of the form

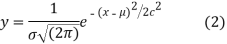
Where μ and are the mean and standard deviation respectively..

The normal distribution is the utmost broadly identified P.D. Then it defines many usual spectacles.

The PDF of the normal distribution is shown by method

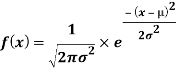
Where μ is mean of the distribution, and  is the variance.

The 2 limitations μ and σ completely describe the figure and all additional things of the normal distribution function.

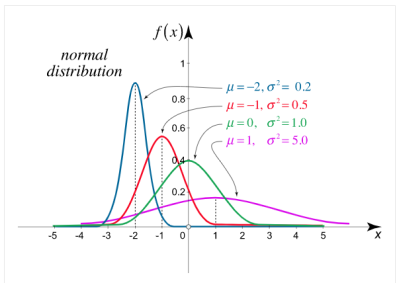Example. X is a normal variate with mean 30 and S.D. 5, find the probabilities that

(i)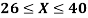               

(ii)            

(iii)          |X-30|≥5

Solution. We have μ =30 and 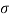=5

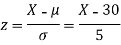
(i)                When X = 26,z = -0.8, when X =40, z =-2

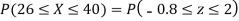
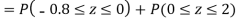
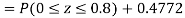
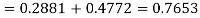
(ii)              When X =45, z =3

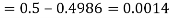
(iii)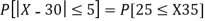          

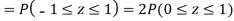
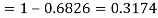
Example. In a normal distribution 31% of the items are under 45 and 8% are over 64. Find the mean and standard deviation of the distribution.

Solution.

Let 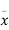be the mean and 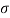the standard deviation 31% of the items are under 45 means area to the left of the ordinate x = 45 (figure 26.6)

When x = 45, let z

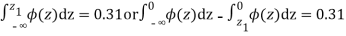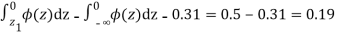
From table III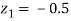

When x = 64, let 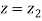so that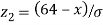

Hence,

From table III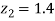

From (i) and (ii),

From (iii) and (iv),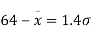

Solving these equations we get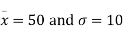

Example. In a test on 2000 electric bulbs, it was found that the life of a particular make was normally distributed with an average life of 2040 hours and standard deviation of 60 hours. Estimated number of bulbs likely to burn for

1. More than 2150 hours
2. Less than 1950 hours and
3. More than 1920 hours and but less than 2 160 hours

Solution

Here μ = 2040 hours and 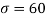hours

(a)  For x = 2150,

Area against z = 1.83 in the table III = 0.4664

We however require the area to the right of the ordinate at z = 1.83. This area = 0.5-0.4664=0.0336

Thus the number of bulbs expected to burn for more than 2150 hours.

= 0.0336×2000 = 67 approximately

(b) For x = 1950,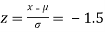

The area required in this case is to be left of z = -1.33

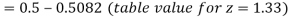
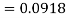
Therefore the number of bulbs expected to burn for less than 1950 hours

(c)  When x = 1920,

When x = 2160,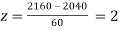

The number of bulbs expected to learn for more than 1920 hours but less than 2160 hours will be represented by the area between z = -2 and z = 2. This is twice the area from the table for z =2, i.e. 2 × 0.4772=0.9544

Thus required number of bulbs = 0.9544 × 2000 = 1909 nearly

Example. If the probability of committing an error of magnitude x is given by

Compute the probable error from the following data:

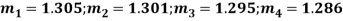
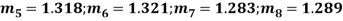
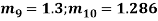
Solution. From the given data which is normally distributed, we have

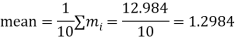
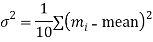
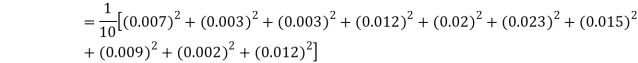
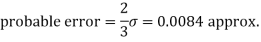
Gamma density

Consider the distribution of the sum of 2autonomous Exponential(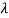) R.V.

Density of the form:
 

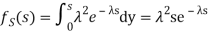
Density is known Gamma (2, density. In common the gamma density is precise with 2 reasons (t,  as being non zero on the +ve reals and called:
 

Where F (t) is the endless which symbols integral of the density quantity to one:
 

By integration by parts we presented the significant recurrence relative:

Because 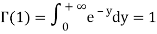, we have for integer t=m
 

The specific case of the integer t can be linked to the sum of n independent exponential, it is the waiting time to the nth event, it is the matching of the negative binomial.

From that we can estimate what the estimated value and the variance are going to be: If all the Xi's are independent exponential (, then if we sum n of them we

Have  and if they are independent: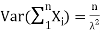 

This simplifies to the non-integer t case:

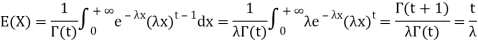
Example1:Following probability distribution

X	0	1	2	3	4	5	6	7
P(x)	0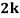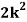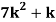

Find: (i) k   (ii)

(i)                Distribution function

(ii)             If 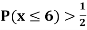  find minimum value of C

(iii)          Find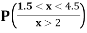

Solution:

If P(x) is p.m.f –

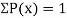
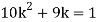
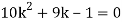
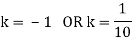
(i)

X	0	1	2	3	4	5	6	7
P(x)	0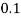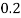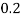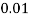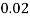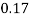

(ii)

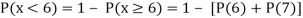
(iii)

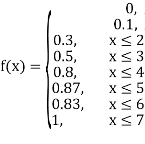
(iv)

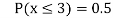
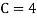
(v)

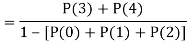
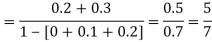
Example 2. I choose real number uniformly at random in the interval [a, b], and call it X. Buy uniformly at random, we mean all intervals in [a, b] that have the same length must have the same probability. Find the CDF of X.

Solution.

Since we conclude

Now, let us find the CDF. By definition thus immediately have

For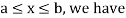

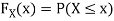
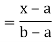
Thus, to summarize

Note that hear it does not matter if we use “<” or “≤” as each individual point has probability zero, so for example 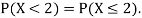Figure 4.1 shows the CDF of X. As we expect the CDF starts at 0 at end at 1.

Example 3.

Find the mean value μ and the median m of the exponential distribution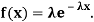

Solution. The mean value μ is determined by the integral

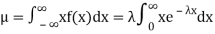Integrating by parts we have 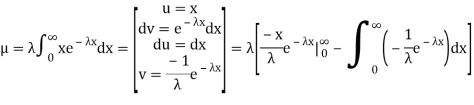We evaluate the second term with the help of 1 Hopital's Rule: 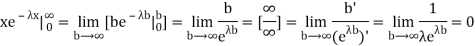Hence the mean (average) value of the exponential distribution is 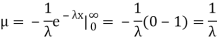Determine the median m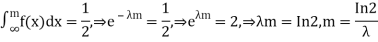

Key takeaways-

References:

 1. E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.

 2. P. G. Hoel, S. C. Port and C. J. Stone, “Introduction to Probability Theory”, Universal Book Stall, 2003.

3. S. Ross, “A First Course in Probability”, Pearson Education India, 2002.

 4. W. Feller, “An Introduction to Probability Theory and its Applications”, Vol. 1, Wiley, 1968.

 5. N.P. Bali and M. Goyal, “A text book of Engineering Mathematics”, Laxmi Publications, 2010.

 6. B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.

 7. T. Veerarajan, “Engineering Mathematics”, Tata McGraw-Hill, New Delhi, 2010.