Unit - 2

Z- Transforms

2.1 The Z-transform: Definition

The Z transform for discrete time system x(n ) is defined as

X(z) = 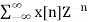        ------- (1) where z is a complex variable.

In polar form z can be expressed as

z  = r e jw ---------------(2) where r is the radius of a circle.

For n≥ 0

X(z ) = 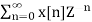       --------- (3)which is called one-sided z-transform.

By substituting z = r e jw

X(r e jw)  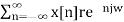=                                           ------- (4)

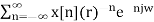                              ----- (5)

Equation(5) represents the Fourier transform of the signal x(n) r-n

Hence the inverse DTFT  X(r ejw) must be x(n) r-n.

x(n) r-n = 1/2π r e jw)  e jwndw

On multiplying both sides by rn  we get

x(n) = 1/ 2 π   r ejw) (r ejw )ndw                  [ z = r ejw

Let z= r e jw  anddw= dz/jz 

Dz = r ejwdw

Dw = dz/jrejw

x[n] =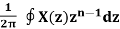

Example

Find the z-transform for the sequence

x[n] = 2 δ[n]+ 3 δ[n-1]+ 5 δ[n-2]+ 2 δ[n-3]

Solution:

X(z) = 2 + 3 z-1 + 5 z -2 + 2 z -3   

Example

If X(z)= 4 – 5 z-2 + z-3 – 2z -4    then find x[n]

Solution:

x[n] = 4 δ[n] - 5 δ[n-2] + δ[n-3] - 2 δ[n-4]

Key Takeaways:

The Z transform is the discrete time analog of the Laplace transform

2.2 Properties of the region of convergence for the Z-transform

Properties of Region of Convergence

1. The ROC is a ring or disk in z-plane centered at the origin.
2. The ROC cannot contain any poles.
3. If x(n) is finite duration casual sequence then the ROC is the entire z-plane except at z=0.
4. If x(n) is a finite duration anti-casual sequence then the ROC is the entire z-plane except at z=∞.
5. If x(n) is a finite duration two- sided sequence the ROC is entire z-plane except at z=0 and z=∞.
6. If x(n) is infinite duration two- sided sequence ROC will consist of a ring in z-plane bounded on the interior and exterior by a pole not containing any poles.
7. The ROC of an LTI stable system contains the unit circle
8. ROC must be connected region.

2.3 Z-transform properties

Linearity

If X1(z) = Z{x1(n)} and X2(z) = Z{x2(n)}

Then

Z{ax1(n) + bx2(n)} = a X1(z) + b X2(z)

Proof:

Z{ax1(n) + b x2(n) }=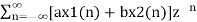                         

= a 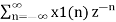 + b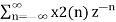     

= a X1(z) + b X2(z)

Time Shifting

If X(z) = Z{x(n)} and initial conditions for x(n) are zero then

Z{x(n-m) } = z-m X(z)

Where m is a positive integer.

Proof:

Z {x(n-m)} = 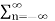x(n-m)z-n         

Let n-m = p then n= p+m

Z{x(n-m)} = 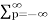 x(p) z-(m+p)                        

z-m 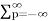x(p) z-p= z-m X(z)

Multiplication by exponential sequence

If X(z ) = Z{x(n)} then

Z [ an x(n) ] = X(a-1 z)

Proof:

Z{ an x(n) } = 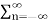x(n) an z-n

= x(n)   (az-1)n 

= X(az-1)

Convolution

We know that

Z{x(n) * h(n) } = X(z) H(z)

Proof:

Let y(n) = x(n) * h(n)

y(n)= 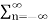x(k)h(n-k)

Taking z-transform on both sides we obtain

Y(z) = [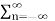x(k)h(n-k)]z-nn

x(n) z-k 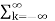h(n-k)   z –(n-k)       Replacing n-k by l

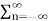x(k)  z-k 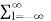h(l)   z-l

= X(k) Z(k)

Time Reversal

If X(z) = Z{x(n)} then

Z{x(-n)} = X(z-1}

Proof:

Z{x(-n)} = 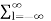h(l)   ( z-l) -1           l=-n

= X(z-1)

Multiplication by n

If Z{x(n)} = X(z) then

Z{n x(n)} = -z d/dz X(z)

X(z) = x[n]z-n   

Z{n x(n)} = 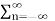nx[n]z-n 

= zx[n]z-n 

=

= 

=

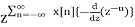
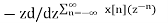
= -z d/dz X(z)

Problems:

1. Find the z-transform of the sequence

x(n) = a n-1 u(n-1)

We know that x(n) = an u(n)  is

X(z) = 1/1/az-1

By using time shifting property we have Z{ x(n-k)} = z-k X(z)

Therefore

Z{an-1 u(n-1)} = z-1/ 1-az-1  = 1/z-a.            ROC |z| > |a|

2.Find the z-transform of the sequence

x(n) = an cos nπ/2

Z{ cos w0n} = 1- (cos w0) z-1/ 1 –(2 cos w0) z-1 + z-2   

Since w0=π/2

Z{ cos π/2 n u(n)} = 1/1 + z-2

Using exponential sequence property

Z{ an x(n) } = X(a-1 z)

Z{ an cos nπ/2} = 1/1+(a-1z)-2 = 1/ 1 + a2/z2  = z2/ a2 + z2  

3.Find the z transform of the sequence x(n) = n u(n)

The z-transform of unit step sequence is given by

Z{u(n)} = z/z-1

Z{ n u(n)} = -z d/dz (z/z-1)

= z/(z-1)2    

4.If x(n) = x1(n) * x2(n) where x1(n) = (1/3)n u(n) and x2(n) = (1/5)n u(n). Find X(z) by using convolution property.

X1(z) = 1/ 1- (1/3)z-1         X2(z) = 1/1- (1/5) z-1 

X(z) = 1/1-(1/3)z-1 . 1/1-(1/5) z-1  

Using z-transform find the convolution of two sequences.

x1(n) = {1,2,-1,0,3}        x2(n) = { 1,2,-1}

Z{ x1(n) * x2(n)} = X1(z) . X2(z)

X1(z) = 1 + 2z-1 – z-2 + 3 z-4

X2(z) = 1 + 2z-1 – z-2 

(1 + 2z-1 – z-2 + 3 z-4  )  (1 + 2z-1 – z-2  )

= 1 + 4z-1 + 2z-2 – 4 z- 3 + 4 z-4 + 6 z- 5 – 3 z-6 

5.Determine the z-transform of the signal

x(n ) = rn (sin w0n ) u(n)

Z{(sin w0n ) u(n)}  = sin w0 z-1/ 1 -2 (cos w0) z-1 + z-2

Z{ an x(n)} = X(a-1 z)

Therefore

Z{ rn sin(w0n) u(n) } = (sin w0) (r-1 z)-1/ 1- 2 (cos w0)(r-1z)-1 + (r-1z)-2  

= r(sinw0) z-1/ 1-2r(cos w0) z-1 + r2 z-2

6.Determine the signal x(n) whose z-transform is given by

X(z) = log(1- az-1).

X(z)= log(1-az-1)

Differentiating both sides we get

d/dz X(z) = 1/1-az-1 (a z-2) = az-2/1- az-1

-z d/dz{ X(z)} = -az-1/1-az-1

= -az-1[ 1/1-az-1]

= -a Z[ a n-1 u(n-1)]                           -------- (1)

From differentiation property

Z{ n x(n)} = -z d/dz [ X(z)]            ------- (2)

Comparing (1) and (2) we get

n  x(n) = -a [ a n-1 u(n-1)]

Or x(n) = -a [a n-1 u(n-1)]/n

7.Determine the z-transform of the signal

x(n) =1/2 (n2 + n) (1/3) n-1 u(n-1)

=½ n2 (1/3) n-1 u(n-1) +1/2 n (1/3) n-1 u(n-1)

We know that

Z[(1/3) n u(n)] = z/ z-1/3

Using time-shifting property

Z{(1/3) n-1 u(n-1)] = 1/ z- 1/3

Z [ n (1/3) n-1 u(n-1)] = -z d/dz [1/z-(1/3)]

=-z d/dz( 1/z-1/3)= -z [-1/(z-1/3) 2]= z/ (z-1/3)2

Z [ n2 (1/3) u(n-1)] = -z d/dz [ z/(z-1/3)2]

= z(z+1/3)/(z-1/3)2 

= -z [ (z-1/3)2 -2z(z-1/3)/(z-1/3)4

= z(z+1/3)/(z-1/3)3 

X(z) = ½[z(z+1/3)/(z-1/3)3 + z/ (z-1/3)2]

= z2/(z-1/3)3

8.Find the z-transform and ROC of the signal

x(n) = an u(n)

Solution: 

X(z) =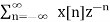 

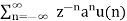=            -----(1)    u(n) = 0 for n<0

1 for n≥0

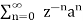= ------- (2)

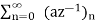=                                      ------- (3)

This is a geometric series of infinite length that is

a + ar + ar2 + ………….. ∞ = a /1-r if |r| <1

Then from equation (3) it converges when |az-1| < 1 or |z| >|a|

Therefore

X(z) = 1/ 1-az-1:  ROC    |z| > |a|

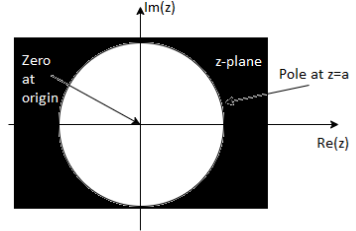
9.Find the z-transform of the signal x(n) =-b n u(-n-1). Find ROC

X(z) =  =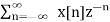 

X(z) = 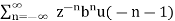                                                                                               u(-n-1) =0 for n ≥0

= 1 for n ≤ -1

=     =  =

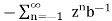= b-1z/1- b-1z = z/ z-b = 1/ 1-bz-1                                                               |z| < |b|

10. Find the z-transform of x(n) = an u(n) – bn u(-n-1)

X(z) =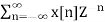  

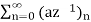=        +  b-1

= z/z-a + z/z-b       ROC |a| < |z| < |b|

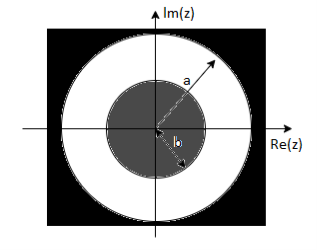
|b|< |a|

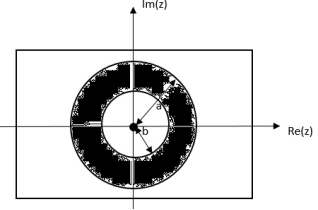
|b| >|a|

11. Find the z-transform of x(n) = {1,2,3,2}

Givenx(0) = 1  x(1) =2   x(2) =3    x(3) = 2

X(z) =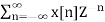 

X(z) = 1+ 2z-1 + 3 z-2 +2 z-3 

Key takeaway

2.4 Inverse Z-transform

Inverse Z transform using partial fraction and power series method

Formal inverse z-transform is based on a Cauchy integral

• Less formal ways sufficient most of the time – Inspection method – Partial fraction expansion – Power series expansion

• Inspection Method – Make use of known z-transform pairs such as

anu[n]  1/ (1-az-1)   |z|  >  |a|

Power series method

The z-transform of the sequence x(n) is given by

X(z) =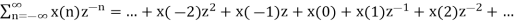

Gives the expansion in power series form. From power series we get the following sequence:

x(n) = {∙∙∙∙∙∙∙∙∙∙x(−2), x(−1), x(0), x(1), x(2), ∙∙∙∙∙∙∙∙∙∙∙}

It is possible to get the power series expansion directly or by long division. In power series expansion technique ROC has a vital role.

Partial fraction expansion method

Find the partial fraction method of

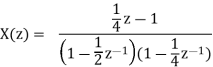
By solving A= 1 and B=-1

Therefore,

X(z) =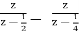

x(n) = (1/2) n u(n) – (1/4) n u(n)

Find the partial fraction of

X(z) =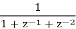

X(z) =

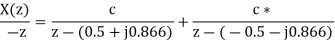
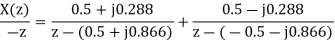
By taking inverse z-transform both sides we get

=(0.5 +j 0.288)((- 0.5 + j 0.866)n u(n)+(0.5 + j 0.288)((-0.5 – j 0.866)n u(n)

Solution of difference equations using Z transform

Z transform converts the difference into algebraic equation in z-domain.

Find the impulse response and step response for the following systems:

y(n) = -  ¾ y(n-1) + 1/8 y(n-2) = x(n)

y(n)  - ¾ y(n-1) + 1/8 y(n-2) = x(n)

Taking z-transform on both sides we get

Y(z) – ¾ [ z-1 Y(z) + y(-1) ] +1/8 [ z-2 Y(z) + z-1 y(-1)+y(-2)] = X(z)

Substituting y(-1)=y(-2)= 0

Y(z) -3/4 z-1 Y(z) + 1/8 z-2 Y(z) = X(z)

Y(z) =

Impulse response

x(n) = δ(n)       X(z) =1

Y(z) = =

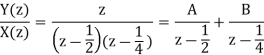
By solving A=2 and B=-1.

Y(z) =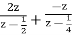

y(n) = 2 (1/2)n u(n) – (1/4) n u(n).

Step Response

x(n) = u(n) X(z) = z/z-1

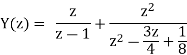
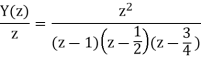
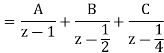
By solving A=8/3   B= -2  C= 1/3

Therefore

Y(z) =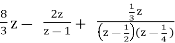

y(n) = 8/3 u(n) – 2(1/2)n u(n) +1/3 (1/4) n u(n)

Que) Find the inverse z-transform of X(z)= 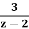. Using partial fraction method. ROC |z|>2?

Sol: X(z)=

Dividing both sides by z

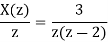
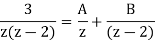
3=A(z-2)+Bz

Equating coefficients of z and z0 on both sides we get

A+B=0

-2A+B=3

Solving above two equations and we get A=-3/2   and B=3/2

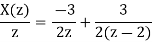
X(z)=

Taking inverse of above equation

X[n]= δ(n)+ (2)nu(n)        

Key takeaway

The methods used for finding inverse z-transform are partial fraction method and power series method.

2.5 Parseval’s theorem

Consider two periodic signals x1(t) and x2(t) with equal period T. If the Fourier series co-efficient of these two signals are cn and dn then

1/T x2(t)   =  1/T 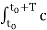n  e j n Ωot [  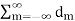e jmΩot  ]    dt---------------------(1)

= 1/T   d *m 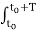 e j(n-m)Ωot  dt ------------------------------(2)

= 0     n≠ m

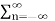
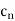= d *n   n=m --------------------------------(3)

If x1(t) = x2(t) = x(t) then eq(3) becomes

1/T |x(t)|2 = 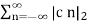                  --------------------------------(4)

The above equation can be written as

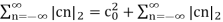
n≠0      

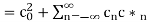
n≠0 

a0 2 + 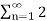[Re(c 2 n ) + Im (cn ) 2]

= a0 2 + n /2 + b 2 n /2 ---------------------------(5)

Key Takeaway:

1. Definition of Parsevals theorem
2. Derivation of the theorem

2.6 Unilateral Z-transform

• The Unilateral z-transform is also called as one-sided z- transform.
• It is defined for n>=0  i.e. Causal sequences.
• The unilateral z- transform is used to solve difference equations with initial conditions.

X(z) =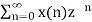

• Unilateral and bilateral transforms are same for causal signals.

Properties of Unilateral Z transform

Time Shift

x(n) ⇌ X(z)

x(n-1) ⇌ z-k X(z) + z-k+1 x(-1)+ ---------------- + z-1x(-k+1) + x(-k)

x(n) ⇌ X(z)

x(n-1) ⇌ Y(z)

Y(z) =

Let n – 1 = m

Y(z) =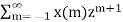

Y(z) = x(-1) + z-1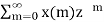

x(n-1) ⇌ z-1 X(z) + x(-1)

x(n – 2) ⇌ z-2 X(z) + z-1x(-1) + x(-2)

Final Value Theorem

x(∞) =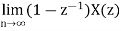

Final value and initial value theorems are valid only for causal and stable system.

x(n+1) ⇌ z X(z) – zx(0)

x(n) ⇌ X(z)

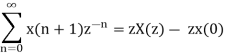
X(z) =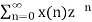

Substracting these two equations

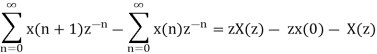
Taking the limit as    z ⟶ 1

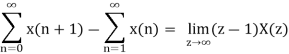
Let us expand the LHS os the above equation as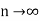   

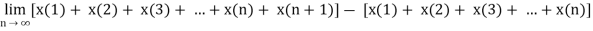
x(∞) =

Or

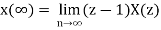
Initial Value Theorem

x(n) ⇌ X(z)

x(0) =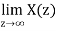

X(z) =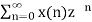

X(z) = x(0) + x(1)/z + x(2)/z2 + ...

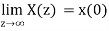
References:

1. Digital signal processing- A practical approach Second Edition, 2002.E. C. Ifeachar, B. W. Jarvis PearsonEducation

2. Sanjit K. Mitra, ‘Digital Signal Processing – A Computer based approach’

3. S. Salivahanan, A Vallavaraj, C. Gnanapriya, ‘Digital Signal Processing’, 2nd Edition McGraw Hill.

4. A. Nagoor Kani, ‘Digital Signal Processing’, 2nd Edition McGraw Hill.

5.P. Ramesh Babu, ‘Digital Signal Processing’ Scitech