Unit - 2
EHVAC Transmission
Need for EHV Transmission
- Increase in size of generating units - transmission of large amounts of power over long distances is technically and economically feasible only at voltages in the EHV and UHV range.
- Pithead steam plants and remote hydro plants - EHV Transmission Systems are needed to transmit large amount of power over long distances from these plants to load centres.
- Surge impedance loading.
- Transmission- The number of circuits and the land requirement for transmission decreases with the adoption of higher transmission voltage.
- Line costs- The line installation cost per MW per km decreases with increase in voltage level.
The following voltage levels are recognised in India as per I5-2026 for line to line voltages of 132 KV and higher.
Nominal system Voltage kV 132 220 275 345 400 500 750
Maximum operating Voltage kV 145 245 300 362 420 525 765
When the line resistance is neglected, the power that can be transmitted depends upon
a) the magnitudes of voltages at the ends (Es, Er).
b) their phase difference , and
, and
c) the total positive sequence reactance X per phase, when the shunt capacitance admittance is neglected.
Thus, P = EsEr sin /(L.X)
/(L.X)
Where P = power in MW, 3 phase
Es, Er = voltages at the sending end and receiving end respectively in kV line-line
 = phase difference between Es and Er
= phase difference between Es and Er
X = positive sequence reactance per phase , ohm/km
And L = line length, km
From consideration of stability, 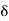 is limited to about 30° and for a preliminary estimate of P, we will take
is limited to about 30° and for a preliminary estimate of P, we will take
Es = Er = E. Thus, the power handling capacity of a single circuit is
P= E² sin 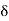 /LX
/LX
At unity power factor, at the load P, the current flowing is
I = E sin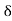 /√3 LX
/√3 LX
And the total power loss in the 3 phases will amount to
Ploss = 3 I²rL = E²sin²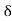 [r/Lx²]
[r/Lx²]
Therefore, the percentage power loss is
% P = (Ploss × 100 /P) = 100. Sin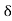 (r/X)
(r/X)
System kV | 400 | 750 | 1000 | 1200 |
X/r | 10.55 | 20 | 64.2 | 85.6 |
% Power loss Line-length km | 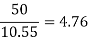 | 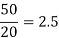 | 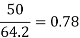 | 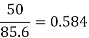 |
a) The power handling capacity of line at a given voltage level decreases with line length being inversely proportional to the length L.
b) Based on current rating, the smaller size of conductor will increase the danger of High Voltage effects giving rise to Corona on the conductors and intensifying radio interference levels and audible noise as well as Corona loss.
c) The percentage power loss in transmission remains independent of line length.
d) Percentage power loss decreases as the system voltage is increased.
Example 1
A power of 12000 MW is required to be transmitted over a distance of 1000 km at voltage levels of 400 KV, 750 KV, 1000 kV and 1200 KV, determine
i) possible number of circuits required with equal magnitudes for sending and receiving end voltages with 30° phase difference.
Ii) the currents transmitted
Iii) the total line losses.
Soln.
Voltage levels KV | 400 | 750 | 1000 | 1200 |
X Ohm/km(50Hz) | 0.327 | 0.272 | 0.231 | 0.231 |
R Ohm/km | 0.031 | 0.0136 | 0.0036 | 0.0027 |
Omit series-capacitor compensation.
P=0.5E2/LX , MW 244.64 1150 2400 3450
a) No. Of circuits
=12000/P 50 12 6 3-4
I = E sin /√3 LX
/√3 LX
b) Current, kA 17.6 9.23 6.925 5.75
c) % Power loss, P 4.76 2.5 0.78 0.584
Total Power loss, MW 571 300 93.6 70
Example 2
A Power of2000 MW is to be transmitted from a super thermal power station in Central India over 800 km to Delhi. Use 400 KV and 750 KV alternators. Suggest the number of circuits required with 50% series capacitor compensation and calculate the total power loss and loss per km.
Soln. With 50% of line reactance compensated, the total reactance will be half of the positive sequence reactance of the 800 km line.
P = 0.5 × 400²/400 × 0.327 = 670 MW/ckt at 400kV
And P = 0.5 × 750²/400 × 0.272 = 2860 MW/ckt at 750 Kv
| 400 kV | 750 kV |
No. Of ckt. Required | 3 | 1 |
Current per ckt., kA | 667/(√3×400) =0.963 | 1.54 |
R for 800km , ohms | 0.031×800 =4.8 | =0.0136 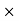 =10.88 |
Loss per ckt, MW | 3×24.8×0.9632 =69MW | 3×10.88×1.542 =77.4 MW |
Total power loss, MW | 3×69 =207 | 77.4 |
Loss/km, kW | 86.25 kW/km | 97 kW/km |
The name Corona has been derived from the glow surrounding the conductors when the operating voltage is sufficiently high. For an overhead transmission system, the atmospheric air which is the dielectric medium, behaves practically like a perfect insulator when the potential difference between the conductors is small. If the voltage impressed between conductors is of alternating nature, sustained charging current will flow due to the capacitance of the line. With the increase of the voltage, there is corresponding increase in the electric field intensity.
As long as the air is subjected to a uniform electric field intensity of peak value less than 3 × 106 V/m (3000 kV/m or 30 kV/cm) , the flow of current between the two conductors of the line is negligibly small for practical purposes. But when the electric field intensity (voltage gradient) reaches this critical value of 3 × 106 V/m, the air in the immediate vicinity of conductors no more remains a dielectric but it ionises and becomes conducting. This electric breakdown is accompanied by following phenomena:
1) A faint glow appears around the conductors which is visible in the dark.
2) There is an acoustical noise.
3) There is a tendency in the conductors to vibrate.
4) Ozone and oxides of Nitrogen are produced.
5) There is loss of Power
6) There is radio interference.
If the voltage gradient is increased further, the size and brightness of the luminous envelope goes on increasing until finally a spark or arc is established between the conductors because of complete breakdown of the insulating properties of the air between them.
The minimum voltage at the at which the breakdown of the insulating properties of air occurs and Corona starts is called the disruptive critical voltage.
The potential gradient corresponding to this value of the voltage is known as disruptive critical voltage gradient.
a) Disruptive critical voltage for a single phase line
Let E = voltage between the conductors (line to line) , volts
r = radius of each conductor in m
D = spacing between the conductors, in m
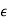 = 8.854 × 10 -12 permittivity of air
= 8.854 × 10 -12 permittivity of air
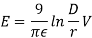
The electric field intensity or voltage gradient at the conductor surface of radius r is given by
E = 2r Gr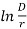
Where Gr =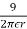 V/m
V/m
Let E0 max = maximum value of disruptive critical voltage, in volts
G0 max = maximum value of disruptive critical voltage gradient in V/m
E0 max = 2r G0 max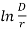
But G0 max = 3×106 V/m
E0 max = 2r×3×106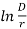
The rms value of the disruptive critical voltage for a single phase line is given by
E0 = 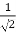 E0 max =
E0 max =  × 6×106 r
× 6×106 r 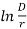 V
V
After considering surface factor m0 and relative air density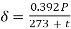
Where r and D are in meters,
E0 = × 6×106 r
× 6×106 r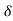 m0
m0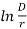 Volts
Volts
b) Disruptive critical voltage for a three phase line.
Let En = line to neutral voltage in volts.
(Phase voltage in volts)
Deq = equivalent spacing between the conductors in m = (Dab Dbc Dca)1/3
r = radius of each conductor in M
Then, En =
En =rGr 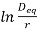
E0 max = r G0 max 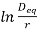
The rms value of the disruptive voltage for a three phase line given by
E0 =  E0 max =
E0 max = 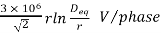
After considering surface factor m0and relative air density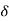 where r and Deq are in meters.
where r and Deq are in meters.
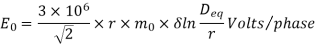
Visual glow of Corona occurs at voltage higher than the disruptive critical voltage. The minimum voltage at which the visual Corona begins is termed as visual critical voltage.
According to FW peek, the actual visual Corona does not start at the disruptive critical value of voltage. The maximum value of voltage gradient responsible for starting of Corona is 3 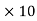 6 V/m. But this value of the voltage gradient at the surface of the conductor will not ionize the air. The maximum value of 3
6 V/m. But this value of the voltage gradient at the surface of the conductor will not ionize the air. The maximum value of 3 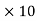 6 V/mwill cause ionization when this value is reached at a distance of (r+0.301√r) from the conductor axis, where r is in metres.
6 V/mwill cause ionization when this value is reached at a distance of (r+0.301√r) from the conductor axis, where r is in metres.
If the maximum voltage gradient at the surface of conductor be3  6 V/m, the value of the maximum voltage gradient at any other point away from the centre would be less than this and thus there will be corona discharge at that point.
6 V/m, the value of the maximum voltage gradient at any other point away from the centre would be less than this and thus there will be corona discharge at that point.
For single phase line,
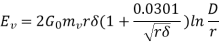
If G0 = 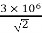 V/m
V/m
Then, 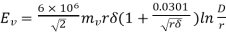 rms volts
rms volts
For three phase line,
 volts/phase
volts/phase
If G0 = 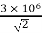 V/m
V/m
Then, 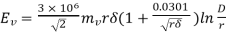 rms volts/phase
rms volts/phase
It should be noted that r, D and Deq are to be taken in metres.
mv = roughness factor or irregularity factor
mv = 1.00 for smooth conductor
mv = 0.7 to 0.75 for local corona when the effect is first visible at some places along the line.
mv = 0.8 to 0.85 for decided or general corona along the whole length of the conductor.
Example
A 3 phase 132 KV, 50Hz, 150 km long transmission line consists of three standard aluminium conductors spaced triangularly at 3.8 m between centres. Each conductor has a diameter of 19.53 mm. The surrounding air is at temperature of 30°C and at a biometric pressure of 750 mm of Mercury. If the breakdown strength of air is 21.1 kV (rms) per cm and the surface factor is 0.85, determine the disruptive critical voltage. Also, determine the visual critical voltages for local and general Corona if the surface factors are 0.72 and 0.82 for visual Corona (10 cal) and visual Corona (general) respectively.
Soln. d=19.53mm, r=0.5d = 0.5(19.53)=9.765×10-3 m
Air density factor, 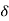 =
= 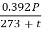
=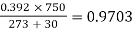
D=3.8m, m0 = 0.85
G0 = 21.1 kV (rms)per cm
=21.1×1000×100 V/m
=2.11×106 V/m
The disruptive critical rms voltage per phase is given by
E0 = G0 m0 r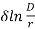
=2.11×106×0.85×9.765×10-3×0.9703×ln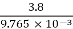
=101.347×103 V
=101.347 kV
For local corona, mv = 0.72
The visual critical rms voltage per phase for local corona is given by

=2.11×106×0.72×9.765×10-3×0.9703[1+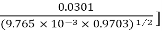 ×ln
×ln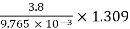 ×5.96
×5.96
=112.396×103 V = 112.393 kV
For decided corona, mv = 0.82
The visual critical rms voltage per phase for decided (general) corona is given by
Ev =2.11×106×0.82×9.765×10-3×0.9703[1+ ×ln
×ln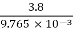
=128×103 V = 128 kV
It is to be noted that there is no corona under normal working conditions since the actual operating voltage to neutral is 132/ √3 that is 76.21kV.
The Corona discharges emit radiations which may introduce noise signals in the communication channels, radio and television receiver in the vicinity. This is called radio interference. Radio noise from overhead power lines is caused by corona on conductors and fittings, surface discharges on insulators and poor contacts and fittings and insulator strings. The Corona discharge which builds up and extinguishers itself in a short period of time of the order of fraction of a microsecond, is called Corona pulse. These pulses are known as Trichel pulses. These pulses are of two types burst and streamer pulses.
The radio and TV interferences increases with the voltage more rapidly than the Corona loss and it is very much influenced by the weather.
Example
Conductors of a three phase transmission line are equilaterally spaced 6 m apart. The radius of each conductor is 1 cm. The air temperature is 30°C and pressure is 740 mm of Mercury. If surface factor is 0.92 and irregularity factor is 0.83, calculate the disruptive critical voltage and visual critical voltage.
Soln. E0=119.475kV(rms value) m0=0.83
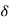 =
= 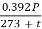
=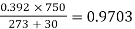
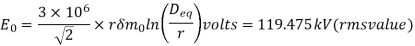
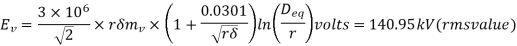
Example
Determine the Corona loss of a three phase, 220 KV, 50 Hz and 200 kilometre long transmission line of three conductors each of radius 1 cm and spaced 5m apart in an equilateral triangle formation. The air temperature is 30°C and the atmospheric pressure is 760 mm of Mercury. The surface factor or irregularity factor is 0.85.
Soln. 
f = 50 Hz 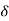 =
=  =
=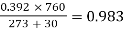
r=1cm=0.01m D=5m
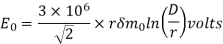
=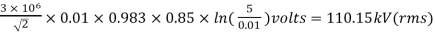
En = 220/ kV = 127 kV
kV = 127 kV
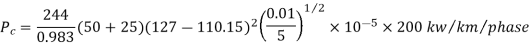
Pc = 472.73 kW/phase
Total corona loss = 3×472.73 kW = 1418.19 kW
Corona Power Loss
The power dissipated in the system due to the Corona discharges is called Corona loss. It is very difficult to estimate Corona loss accurately because of its extremely variable nature.
According to F. W. Peek, Jr, the Corona loss for single phase and equilaterally spaced 3 phase under fair weather conditions is given by the formula-
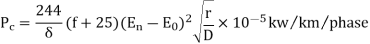
Where
Pc=corona power loss
f=frequency of supply in Hz
 =air density factor
=air density factor
En=rms phase voltage (line to neutral voltage) in kV
E0=disruptive critical voltage per phase in kV (rms)
r = radius of conductor in metres.
D = spacing between conductors in metres.
For single phase line,
En =  ×line voltage
×line voltage
For three phase line,
En = 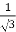 ×line voltage
×line voltage
The total loss of the line is the sum of the losses due to the three conductors. Peek's formula is applicable for decided visual corona. The experimental results indicate that corona takes place even when the voltage between the conductor is well below the disruptive critical voltage.
Peterson’s empirical formula for fair weather loss is
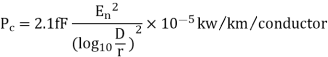
Where Pc = corona power loss
f = frequency of supply in Hz
En = voltage per phase (line to neutral voltage in kV (rms))
r = radius of conductor in metres
D = spacing between conductors in metres
The factor F is called the corona loss function. It varies with the ratio (En/E0).
Factors affecting corona loss
1) Effect of system frequency- The Corona loss varies directly as the system frequency.
2) Effect of system voltage- In the region near the disruptive voltage, the rate of increase of Corona power loss with the increase in system voltage is small but when Vphis large as compared to Vd0, Corona loss increases at a very fast rate with the increase in system voltage.
3) Effect of conductivity of air- Higher air conductivity leads to greater Corona loss.
4) Effect of density of air - Corona loss increases with the decrease in the density of air.
5) Effect of conductor radius- The electric field intensity decreases with the increase in radius of conductor. Hence, with conductors of large radius, electric field intensity decreases resulting in lower Corona power loss.
6) Effect of conductor surface- Roughness of the surface of the conductor causes a field distortion and gives rise to high potential gradient causing higher Corona loss.
7) Effect of atmospheric conditions- Corona loss, particularly local Corona discharges, increases in rain and bad atmospheric conditions, such as fog, sleet and snowstorms.
8) Effect of load current - The heating of the conductor due to flow of load current though it has an indirect reducing effect on the Corona loss. Heating of conductor prevents deposition of due or snow on the surface of the conductor and reduces Corona loss.
9) Bundling of conductors- The value of large diameter will reduce the Corona loss.
- It can be reduced by increasing the diameter of conductor which decreases the corona effect.
- It can be reduced by increasing the space between the conductors.
- The use of conductor in form of bundle can be helpful in reducing the corona effect. Due to use of bundles the diameter of the conductor increases.
- Using round corona rings can help to reduce this effect. These rings are connected to high voltage conductors, which encircles the points of corona and hence reduces the sharpness of the surface of the conductors. Hence, distributing the charge across a wider area.
Example
Estimate the Corona loss for a three phase, 110 KV, 50 Hz, 150 km long transmission line consisting of three conductors each of 10 mm diameter and displaced 2.5 metres apart in an equilateral triangle formation. The temperature of air is 30°C and the atmospheric pressure is 750 mm of Mercury. Take the regularity factor as 0.85. Ionization of air may be assumed to take place at a maximum voltage gradient of 30 kV/cm.
Soln. d = 10mm, r= 0.5d = 5mm = 5 × 10-3 m
Air density factor, 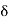 =
= 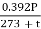
=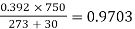
D= 2.5 m, m0 = 0.85
E0 =G0 m0 r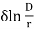 V/phase
V/phase
=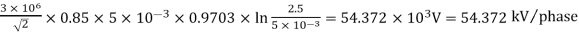
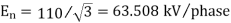
According to peek, corona loss under fair weather conditions is given by

=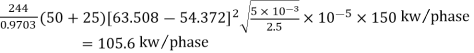
Total corona loss = 3Pc = 3×105.6 = 316.8 Kw
Example-
A three phase,220 KV transmission line with conductors radius 1.3 cm is built so that Corona takes place if the line voltage exceeds 260kV (rms). Find the spacing between conductors.
Soln. Disruptive critical voltage, Vrms =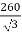 = 150.11 kV
= 150.11 kV
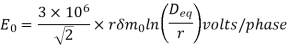
Assuming 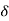 = 1 and m0 = 1 (smooth conductor)
= 1 and m0 = 1 (smooth conductor)
R = 0.013 m E0 = 150.11 kV=150.11×103 volts
150.11×103= 
 5.44
5.44
Deq = 0.013 × e5.44
Deq = 3 m
Example
A Three phase equilateral line has a total Corona loss of 55kw at 110 KV and 100 KW at 114 KV. What is the disruptive critical voltage between lines? What is the Corona loss at 120 KV?
Soln. Power loss due to corona for three phases is given by
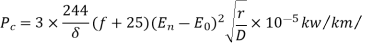
Taking  , f, r and D as constants,
, f, r and D as constants,
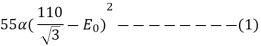
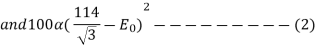
From (1) and (2),

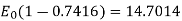
E0 = 57 kV
When Vn = 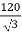
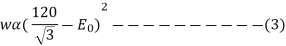
From equation 1 and 3,
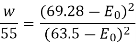

=196.3 kW
Line -line disruptive critical voltage
= √3 × E0
=√3 × 57
= 98.72 kV
Example
Find the disruptive critical voltage and visual Corona voltage (local Corona as well as General Corona) for a 3 phase 220 KV line consisting of 22.26 mm diameter conductors spaced in a 6m Delta configuration. The following data can be assumed.
Temperature 25°C , pressure 73 cm of Mercury, surface factors 0.84, irregularity factor for local Corona 0.72, irregularity factor for general Corona 0.82.
Soln. r = 0.5 × 22.26 = 11.13 mm = 1.113 × 10-2 m
 =
= 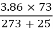 = 0.9456
= 0.9456
m0 = 0.84 D = 6m
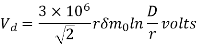
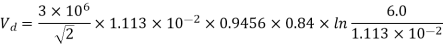
Vd = 11.8×104 V or 118 kV per phase
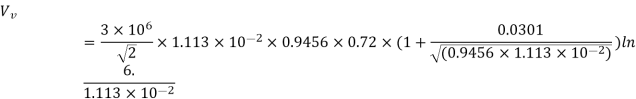
Vv = 13.07 × 104 V or 130.7 kV per phase
For general visual corona mv = 0.82 and
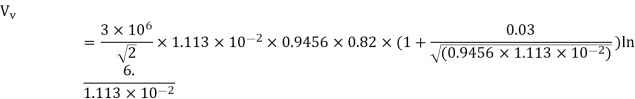
=14.88 × 104 V or 148.8 kV/phase
References:
- H. Hadi Sadat: Power System Analysis, Tata McGraw-Hill New Delhi.
- W. Stagg and El- Abiad – Computer Methods in Power System Analysis – Tata McGraw Hill, New Delhi.
- M.E.El-Hawary, Electric Power Systems: Design and Analysis, IEEE Press, New York.
- Rakash Das Begamudre, “Extra High voltage A.C. Transmission Engineering”, New age publication.
- M.A.Pai, Computer Techniques in Power System Analysis, Tata McGraw Hill Publication.
- Stevenson W.D. Elements of Power System Analysis (4th Ed.) Tata McGraw Hill, New Delhi.