Unit - 2
Delay
Consider the cascade connection of two CMOS inverter circuits shown in Figure below. The parasitic capacitances associated with each MOSFET are illustrated individually. Here the capacitances Cgd and Cgs are primarily due to gate overlap with diffusion, while Cdb and Csb are voltage-dependent junction capacitances. The 'capacitance component Cg is due to the thin-oxide capacitance over the gate area. In addition, we also consider the lumped interconnect capacitance Cint, which represents the parasitic capacitance contribution of the metal or polysilicon connection between the two inverters. It is assumed that a pulse waveform is applied to the input of the first-stage inverter. We wish to analyze the time-domain behavior of the first-stage output, Vout.
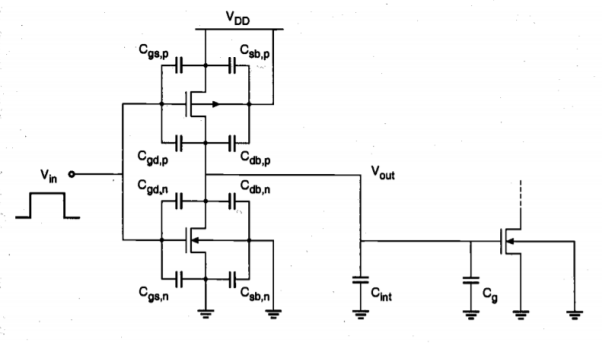
Fig.1 Cascaded CMOS inverter stages.
The problem of analyzing the output voltage waveform is fairly complicated, even for this relatively simple circuit, because a number of nonlinear, voltage-dependent capacitances are involved. To simplify the problem, we first combine the capacitances seen in Figure above into an equivalent lumped linear capacitance, connected between the output node of the inverter and the ground. This combined capacitance at the output node will be called the load capacitance, Cload.
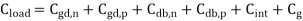
Note that some of the parasitic capacitance components shown in Figure above do not appear in this lumped capacitance expression. In particular, Csbn and CSb have no effect on the transient behavior of the circuit since the source-to-substrate voltages of both transistors are always equal to zero.
The first-stage CMOS inverter is shown with the single lumped output load capacitance Cload in Figure below. Now, the problem of analyzing the switching behavior can be handled more easily. In fact, the question of inverter transient response is reduced to finding the charge-up and charge-down times of a single capacitance which is charged and discharged through one transistor. The delay times calculated using Cload may slightly overestimate the actual inverter delay, but this is not considered a significant deficiency in a first-order approximation.
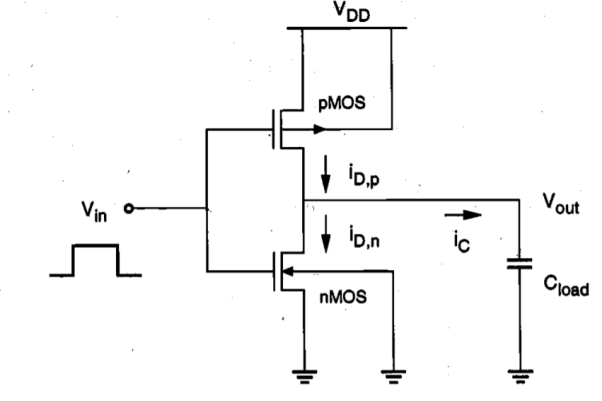
Fig.2 First-stage CMOS inverter with lumped output load capacitance.
Key takeaway
Note that some of the parasitic capacitance components shown in Figure above do not appear in this lumped capacitance expression. In particular, Csbn and CSb have no effect on the transient behavior of the circuit since the source-to-substrate voltages of both transistors are always equal to zero
The input and output voltage waveforms of a typical inverter circuit are shown in Figure below. The propagation delay times 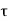 PHL and
PHL and 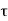 PLH determine the input-to-output signal delay during the high-to-low and low-to-high transitions of the output, respectively. By definition,
PLH determine the input-to-output signal delay during the high-to-low and low-to-high transitions of the output, respectively. By definition, 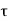 PHL is the time delay between the V50%-transition of the rising input voltage and the V50% -transition of the falling output voltage. Similarly,
PHL is the time delay between the V50%-transition of the rising input voltage and the V50% -transition of the falling output voltage. Similarly, 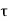 PLH is defined as the time delay between the V50% -transition of the falling input voltage and the V50%-transition of the rising output voltage. To simplify the analysis and the derivation of delay expressions, the input voltage waveform is usually assumed to be an ideal step pulse with zero rise and fall times. Under this assumption, TPHL becomes the time required for the output voltage to fall from VOH to the V50% level, and
PLH is defined as the time delay between the V50% -transition of the falling input voltage and the V50%-transition of the rising output voltage. To simplify the analysis and the derivation of delay expressions, the input voltage waveform is usually assumed to be an ideal step pulse with zero rise and fall times. Under this assumption, TPHL becomes the time required for the output voltage to fall from VOH to the V50% level, and 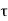 PLH becomes the time required for the output voltage to rise from VOL to the V50% level. The voltage points V50% is defined as follows.
PLH becomes the time required for the output voltage to rise from VOL to the V50% level. The voltage points V50% is defined as follows.

Fig 3 Input and output voltage waveforms of a typical inverter, and the definitions of propagation delay times. The input voltage waveform is idealized as a step pulse for simplicity.
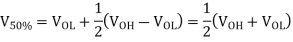
Thus, the propagation delay times  PHL and
PHL and  PLH are found from Figure above as
PLH are found from Figure above as
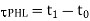
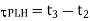
The average propagation delay of 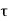 p the inverter characterizes the average time required for the input signal to propagate through the inverter.
p the inverter characterizes the average time required for the input signal to propagate through the inverter.

We will refer to Figure below for the definition of output voltage rise and fall times. The rise I time 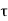 rise is defined here as the time required for the output voltage to rise from the V10% level to V90% level. Similarly, the fall time Tall is defined here as the time required for the output voltage to drop from the V90% level to V10% level. The voltage levels V10% and V90% are defined as
rise is defined here as the time required for the output voltage to rise from the V10% level to V90% level. Similarly, the fall time Tall is defined here as the time required for the output voltage to drop from the V90% level to V10% level. The voltage levels V10% and V90% are defined as
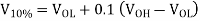

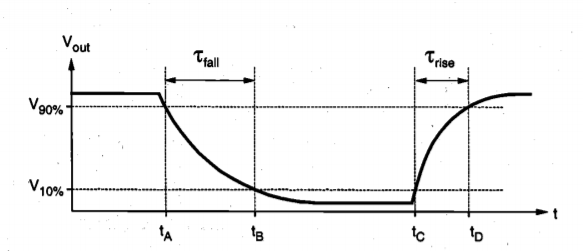
Fig 4 Output voltage rise and fall times.
Thus, the output rise and fall times are found from Figure above as follows.
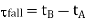
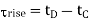
Calculation of Delay Times
The simplest approach for calculating the propagation delay times 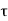 pHL and
pHL and 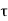 pLH is based on estimating the average capacitance current during charge down and charge up, respectively. If the capacitance current during an output transition is approximated by a constant average current Iavg the delay times are found as
pLH is based on estimating the average capacitance current during charge down and charge up, respectively. If the capacitance current during an output transition is approximated by a constant average current Iavg the delay times are found as

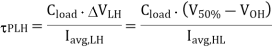
The average current during high-to-low transition can be calculated by using the current values at the beginning and the end of the transition.
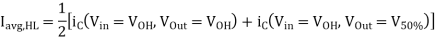
Similarly, the average capacitance current during low-to-high transition is
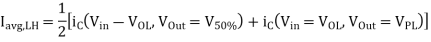
The propagation delay times can be found more accurately by solving the state equation of the output node in the time domain. The differential equation associated with the output node is given below. Note that the capacitance current is also a function of the output voltage.
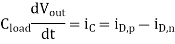
First, we consider the rising-input case for a CMOS inverter. Initially, the output Voltage is assumed to be equal to VOH. When the input voltage switches from low (VOL) to high (VOH), the nMOS transistor is turned on and it starts to discharge the load 0 capacitance. At the same time, the pMOS transistor is switched off; thus,

Note that in other types of inverter circuits, such as the resistive-load inverter or the depletion-load inverter, the load device continues to conduct a nonzero current when the input is switched from low to high. However, the load current is usually negligible in comparison to the driver current. Therefore, above equation can be used to calculate the charge- down time not only in CMOS inverters, but also in almost all common types of inverter circuits.
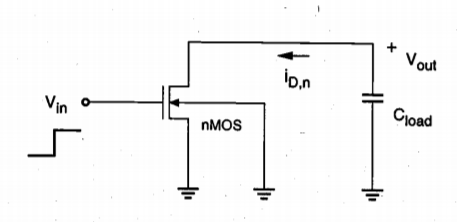
Fig 5 Equivalent circuit of the CMOS inverter during high-to-low output transition.
First, consider the nMOS transistor operating in saturation

For 
Since the saturation current is practically independent of the output voltage (neglecting channel-length modulation),

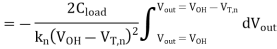
Evaluating this simple integral yields
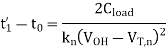
At t = t', the output voltage will be equal to (VDD - VTn) and the transistor will be at the saturation-linear region boundary. Next, consider the nMOS transistor operating in the linear region.
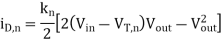
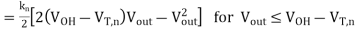
The solution in the time interval between t' and t can be found as
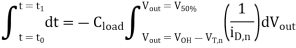
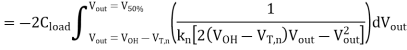
Evaluating this integral yields

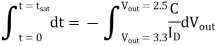
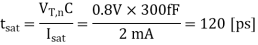
The transconductance kn of the nMOS transistor can be found as follows:
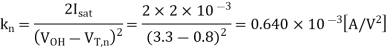
Now, the current equation for the linear operating region is
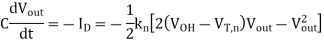
Integrating this differential equation between the two voltage boundary conditions yields the time in which the nMOS transistor operates in the linear region during this transition.
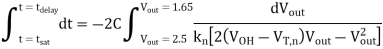
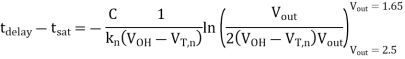
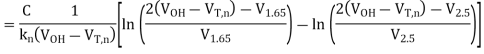
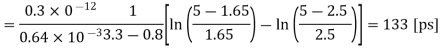
Thus, the total delay time is found to be

Note that tdelay corresponds to the propagation delay time 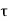 PHL for falling output.
PHL for falling output.

Finally, the propagation delay time for high-to-low output transition (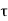 PHL) can be found by
PHL) can be found by
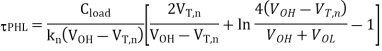
For VOH = VDD and VOL= 0, as is the case for the CMOS inverter
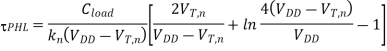
Examples
Q1) Consider the CMOS inverter circuit shown in Figure above, with VDD = 3.3 V. The I-V characteristics of the nMOS transistor are specified as follows: when VGS = 3.3 V, the drain current reaches its saturation level Isat = 2 mA for VDS 2.5 V. Assume that the input signal applied to the gate is a step pulse that switches instantaneously from 0 V to 3.3 V. Using the data above, calculate the delay time necessary for the output to fall from its initial value of 3.3 V to 1.65 V, assuming an output load capacitance of 300 fF.
A1) For the solution, consider the simplified pull-down circuit shown above in explanation of the section. We will assume that the nMOS transistor operates in saturation from t = 0 to t = tsat= t1’, and that it will operate in the linear region from t = tsat= t1’ to t = t2 = tdelay. We can also deduce from the I-V characteristics that VT,n = 0.8 V, since the nMOS transistor enters saturation when VDS > VGS - VT. The voltage VGS is equal to 3.3 V for t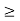 0
0
The current equation for the saturation region can be written as
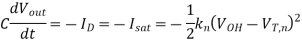
We can calculate the amount of time in which the nMOS transistor operates in saturation (tsat), by integrating this equation. The average-current method presented earlier in this Section can also be used to estimate the propagation delay times as well as the rise and fall times of inverter circuits.
Q2) For the CMOS inverter shown in Figure in explanation of this section with a power supply voltage of VDD = 5 V, determine the fall time 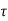 fall which is defined as the time elapsed between the time point at which Vout = V90% = 4.5 V and the time point at which VOut = Vl0% = 0.5 V. Use both the average-current method and the differential equation method for calculating
fall which is defined as the time elapsed between the time point at which Vout = V90% = 4.5 V and the time point at which VOut = Vl0% = 0.5 V. Use both the average-current method and the differential equation method for calculating  fall. The output load capacitance is 1 pF. The nMOS transistor parameters are given as
fall. The output load capacitance is 1 pF. The nMOS transistor parameters are given as  n Cox = 20, uA/V2 (W/L) n = 10, VT,n = 1.0 V
n Cox = 20, uA/V2 (W/L) n = 10, VT,n = 1.0 V
A2) We can determine the average capacitor current during the charge-down event described above.
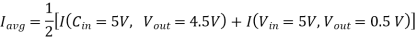
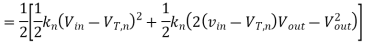
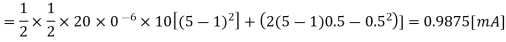
The fall time is then found as
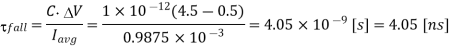
Now, we will recalculate the fall time using the differential equation approach. The nMOS transistor operates in the saturation region for 4.0 V < Vout < 4.5 V. Writing the current equation for the saturation region, we obtain
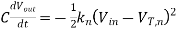 , where
, where 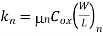
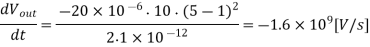
Integrating this simple expression yields the time during which the nMOS transistor operates in saturation.

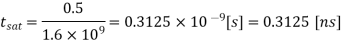
The nMOS transistor operates in the linear region for  . The current equation for this operating region is written as follows:
. The current equation for this operating region is written as follows:
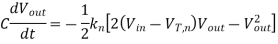
Integrating this equation, we obtain the delay component during which the nMOS transistor operates in the linear region.
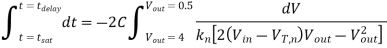
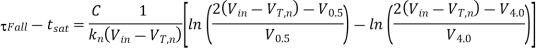
Thus, the fall time of the CMOS inverter is found as follows:
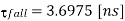
Q3) A company in Urbana, IL called Prairie Technology has access to a CMOS fabrication process with the device parameters listed below.
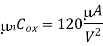
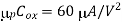
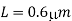 for both nMOS and pMOS devices
for both nMOS and pMOS devices
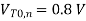
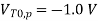
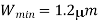
Design a CMOS inverter by determining the channel widths W, and Wp of the nMOS and pMOS transistors, to meet the following performance specifications.
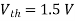 for
for 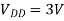
- Propagation delay times
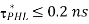 and
and 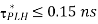
- A failing delay of 0.35 ns for an output transition from 2 V to 0.5V, assuming a combined output load capacitance 300fF and ideal step input.
A3) We start our design by satisfying the time delay constraints. First, the minimum (WIL) ratios of the nMOS and pMOS transistors which are dictated by the propagation delay constraints can be found



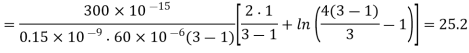
During the falling output transition (from 2 V to 0.5 V) described above, the nMOS transistor of the CMOS inverter will operate entirely in the linear region. The current equation of the nMOS transistor in this region is
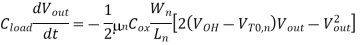
By integrating this expression, we obtain the following relationship
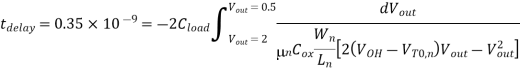

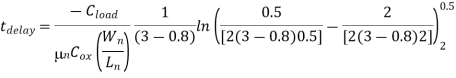
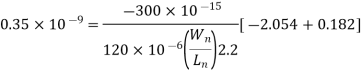
Now we solve this equation for the nMOS transistor (W/L) ratio:
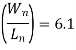
Notice that this ratio is smaller than the (W/L)-ratio found from the propagation delay constraint. Thus, we take the larger ratio which will satisfy both timing constraints, and determine the size of the nMOS transistor as Wn = 4.7 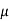 m, for the given Ln, = 0.6
m, for the given Ln, = 0.6 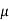 m. Next, the logic threshold constraint of Vth = 1.5 V will help determine the pMOS transistor dimensions.
m. Next, the logic threshold constraint of Vth = 1.5 V will help determine the pMOS transistor dimensions.
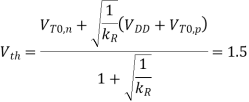
Thus, the total capacitive load of the inverter can now be expressed as
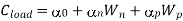
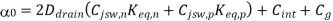
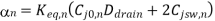
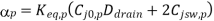
The falling and rising output transitions are rewritten as
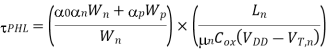
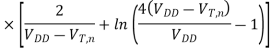
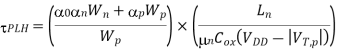
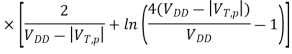
Note that the channel lengths Ln and LP are usually fixed and equal to each other. Also, the ratio between the channel widths Wn and Wp is usually dictated by other design constraints such as noise margins and the logic inversion threshold. Let this transistor aspect ratio be defined as
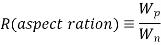

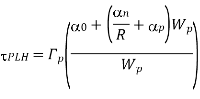
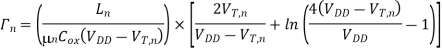
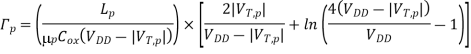
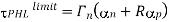
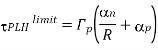
The propagation delay times of a CMOS inverter cannot be reduced ‘beyond these limit values, which are dictated by technology-related parameters such as doping densities, minimum channel length and minimum layout design rules (e.g., Drain). Also, note that the propagation delay limit is independent of the extrinsic capacitance components, Ci, and Cg. How fast this asymptotic limit is approached in a specific case depends on the ratio of intrinsic and extrinsic capacitance components of Cload. If the extrinsic components dominate the total load capacitance, then delay reduction can be achieved for wider range of Wn and We. If, on the other hand, the intrinsic capacitance component is dominant, then the speed limit is reached for smaller values of Wn and Wp
- The RC delay model is a metric used in VLSI design to calculate the signal delay between the input voltage and output voltage of the input signal.
- The input signal is a step function. In this case the transistor can be considered as a switch in series with a resistor.
- A unit nMOS transistor is characterized with resistance or effective resistance, R= Vds/Ids
- Let’s consider a k times transistor unit, here the resistor of the single transistor is R/k, k is the constant here. PMOS transistor has a bigger resistance – 2R.
- NMOS transistors are characterized with higher mobility than pMOS transistors. If the transistor is velocity-saturated, its current and resistance does not depend on the channel length.
- Let’s consider a transistor with gate capacitance C. For a k unit cell, gate capacitance of the transistor is kC.
- Diffusion capacitance depends on the size of drain or source, but with the most common approximation it is also C.

Fig 6 Time Delay

Fig 7 RC Circuit
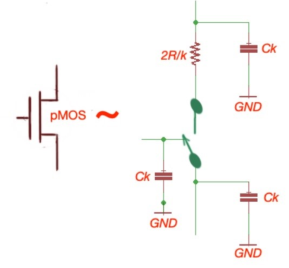
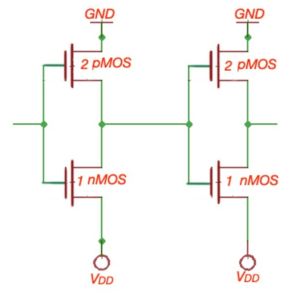
Fig 8: Equivalent RC circuits
Normalized delay of a gate can be expressed as the sum of parasitic delay and effort delay. The effort delay depends on the fan-out of the gate, here is a logical effort.
Electrical effort is a situation when a gate is driving identical to itself gates is said to have an electrical effort or fan-out. In case if the load consists of gates different from driving gate, the electrical effort of fan-out can be found by formula, here is the capacitance of the driving gate, and is the capacitance of the load gates that are being driven.
Logical effort of the gate is the ratio of the input capacitance of the gate to the input capacitance of the inverter that delivers the same output current.
Type of gate | 1 input | 2 inputs | n inputs |
Inverter | 1 |
|
|
NAND |
| 4/3 | 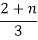 |
NOR |
| 5/3 | 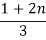 |
XOR |
| 4 |
|
XNOR |
| 4 |
|
When designing the delays in VLSI it is important to take into consideration the following parameters:
- Propagation delay time
- Contamination delay time
- Rise time
- Fall time
- Edge rate
Regarding gates, charging and discharging a node is called the driver, the gate’s wire driven is the load. The propagation delay is called the delay.
The timing analyser computes the signal arrival time. The nodes are classified as the inputs, outputs and internal nodes. The signal arrival time should be taken into consideration and the time data is required at the outputs. The arrival time at the internal node depends on the propagation delay at the gate and the arrival times of the inputs at the gates.
The timing analyser calculates the arrival times at each internal node and checks if the outputs arrive at their required times. The difference between the required and arrival time is the slack. A negative slack means that the circuit meets the required timing. Arrival times can also be calculated based on the contamination times. The summarised data gives the picture of the gate switching parameters.
Timing optimisations
The design structures must always contain the paths that are fast enough or the ones that are critical in terms of the operating times – they are called critical paths. The critical paths can be affected at the following levels:
- Architectural level
- Logic level
- Circuit level
- Layout level.
The best leverage is performed with the good microarchitecture. This level requires the broad knowledge of the both the algorithmic and technological level of the device. The next level is logic. The trade-offs can be made at the stage of the functional blocks, the number of stages of gates in the clock cycle, and at the fan-in and fan-out cycles. The delay can be also be turned at the circuit level, varying the transistor size or using different CMOS techniques. The last level is layout level, when the delay can be set up. Here the delay can be set up with the wiring lengths.
Many device designers never leave the RTL level that creates the design. The standard way to write RTL code is to synthesise it and check if the results are fast enough. The timing analysers are used to check the timing closure, and whether the circuit meets the timing requirements. The lower abstraction level is the best way to adjust and vary the timing parameters.
Timing analysis procedure
Two major steps:
- Build graph with elemental delays;
- Traverse graph to find longest path.
Must model 0-1 and 1-0 delays independently for more accurate total delay. Use value analysis to prune impossible paths.

From above example
- Make assumptions about primary inputs.
- Primitive path delay: RC delay from power supply or primary input to transistor gate or primary output. Primitive path (p0, p1, p2, p3) delays computed from RC analysis.
- Each path forms an edge in timing analysis graph.
- Timing analysis graph is analyzed to find worst-case delay through entire circuit.
- Timing graph structure: The nodes are sources and sinks of primitive delay paths. The edges represent primitive delay paths.
- Use depth-first or breadth-first search to find longest delay path.
- False paths create un exercisable paths which make delay pessimistic. Can be identified using analysis algorithms.
- Some transistor configurations only allow current flow in one direction other direction of current/signal flow is a false path.
Current signal flow analysis
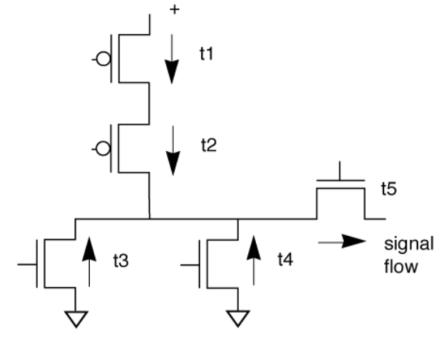
False current path example
- Many paths in barrel shifter cannot be exercised.
- Driver gates enforce current flow in one direction on data lines, eliminating some paths through the pass transistors.
- Path analysis which does not take into account feasible current flow will identify infeasible long paths.
High frequencies impose a strict limit on power consumption in computer systems as a whole [Ref Texas Instruments]. Therefore, power consumption of each device on the board should be minimized. Power calculations determine power-supply sizing, current requirements, cooling/heatsink requirements, and criteria for device selection. Power calculations also can determine the maximum reliable operating frequency. Two components determine the power consumption in a CMOS circuit:
• Static power consumption
• Dynamic power consumption
CMOS devices have very low static power consumption, which is the result of leakage current. This power consumption occurs when all inputs are held at some valid logic level and the circuit is not in charging states. But, when switching at a high frequency, dynamic power consumption can contribute significantly to overall power consumption. Charging and discharging a capacitive output load further increases this dynamic power consumption. This application report addresses power consumption in CMOS logic families (5 V and 3.3 V) and describes the methods for evaluating both static and dynamic power consumption. Additional information is also presented to help explain the causes of power consumption, and present possible solutions to minimize power consumption in a CMOS system.
Key takeaway
Two components determine the power consumption in a CMOS circuit:
• Static power consumption
• Dynamic power consumption
Static Power Consumption
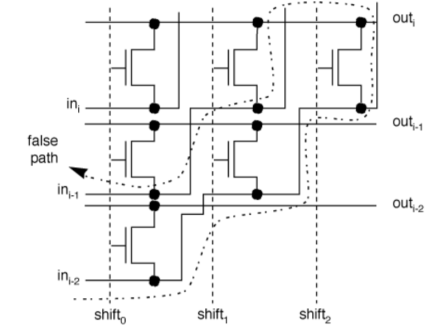
Typically, all low-voltage devices have a CMOS inverter in the input and output stage. Therefore, for a clear understanding of static power consumption, refer to the CMOS inverter modes shown in Figure.
Fig 9 CMOS inverter mode for Static Power Consumption
As shown in Figure above, if the input is at logic 0, the n-MOS device is OFF, and the p-MOS device is ON (Case 1). The output voltage is VCC, or logic 1. Similarly, when the input is at logic 1, the associated n-MOS device is biased ON and the p-MOS device is OFF. The output voltage is GND, or logic 0. Note that one of the transistors is always OFF when the gate is in either of these logic states. Since no current flows into the gate terminal, and there is no dc current path from VCC to GND, the resultant quiescent (steady-state) current is zero, hence, static power consumption (Pq) is zero.
However, there is a small amount of static power consumption due to reverse-bias leakage between diffused regions and the substrate. This leakage inside a device can be explained with a simple model that describes the parasitic diodes of a CMOS inverter, as shown in Figure below.
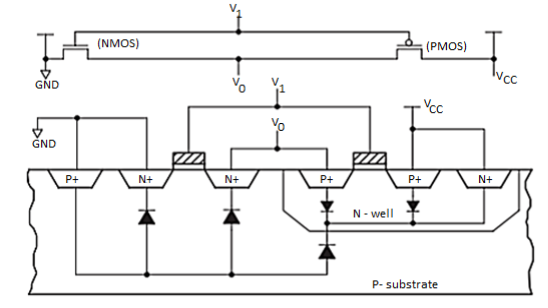
Fig 10 Model Describing Parasitic Diodes Present in CMOS Inverter
The source drain diffusion and N-well diffusion form parasitic diodes. In Figure above, the parasitic diodes are shown between the N-well and substrate. Because parasitic diodes are reverse biased, only their leakage currents contribute to static power consumption. The leakage current (llkg)of the diode is described by the following equation:
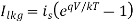
Where
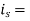 reverse saturation current
reverse saturation current
V = diode voltage
k= Boltzmann’s constant (1.38×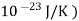
q= electronic charge (1.602 × 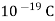 )
)
T = temperature
Static power consumption is the product of the device leakage current and the supply voltage. Total static power consumption, PS, can be obtained as shown in equation
Ps = 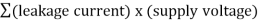
Most CMOS data sheets specify an ICC maximum in the 10-µA to 40-µA range, encompassing total leakage current and other circuit features that may require some static current not considered in the simple inverter model.
The leakage current ICC (current into a device), along with the supply voltage, causes static power consumption in the CMOS devices. This static power consumption is defined as quiescent, or PS, and can be calculated by equation
Ps = Vcc x Icc
VCC = supply voltage
ICC = current into a device
Dynamic Power Consumption
The dynamic power consumption of a CMOS IC is calculated by adding the transient power consumption (PT), and capacitive-load power consumption (PL).
Transient Power Consumption
Transient power consumption is due to the current that flows only when the transistors of the devices are switching from one logic state to another. This is a result of the current required to charge the internal nodes (switching current) plus the through current (current that flows from VCC to GND when the p-channel transistor and n-channel transistor turn on briefly at the same time during the logic transition).
The frequency at which the device is switching, plus the rise and fall times of the input signal, as well as the internal nodes of the device, have a direct effect on the duration of the current spike. For fast input transition rates, the through current of the gate is negligible compared to the switching current. For this reason, the dynamic supply current is governed by the internal capacitance of the IC and the charge and discharge current of the load capacitance. Transient power consumption can be calculated using equation
PT = Cpd x VCC2 x f1 x NSW
Where:
PT = transient power consumption
VCC = supply voltage
fI = input signal frequency
NSW = number of bits switching
Cpd = dynamic power-dissipation capacitance
Capacitive-Load Power Consumption
Additional power is consumed in charging external load capacitance and is dependent on switching frequency. The following equation can be used to calculate this power if all outputs have the same load and are switching at the same output frequency.
PL = CL x VCC2 x fo x NSW (CL is the load per output)
Where:
PL = capacitive-load power consumption
VCC = supply voltage
fO = output signal frequency
CL = external (load) capacitance
NSW = total number of outputs switching
In the case of different loads and different output frequencies at all outputs, above equation is used to calculate capacitive-load power consumption.
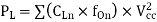
Where
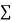 = sum of n different frequencies and loads at n different outputs
= sum of n different frequencies and loads at n different outputs
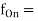 all different output frequencies at each output, numbered 1 through n (Hz)
all different output frequencies at each output, numbered 1 through n (Hz)
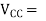 supply voltage (V)
supply voltage (V)
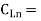 all different load capacitances at each output, numbered 1 through n.
all different load capacitances at each output, numbered 1 through n.
Therefore, dynamic power consumption (PD) is the sum of these two power consumptions and can be expressed as shown
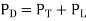
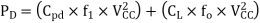
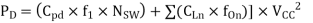
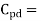 power- consumption capacitance (F)
power- consumption capacitance (F)
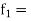 input frequency (Hz)
input frequency (Hz)
 all different output frequencies at each output, numbered 1 through n (Hz)
all different output frequencies at each output, numbered 1 through n (Hz)
 total number of outputs switching
total number of outputs switching
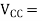 supply voltage (V)
supply voltage (V)
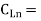 all different load capacitances at each output, numbered 1 through n
all different load capacitances at each output, numbered 1 through n
Total power consumption is the sum of static and dynamic power consumption.

Key takeaway
The dynamic power consumption of a CMOS IC is calculated by adding the transient power consumption (PT), and capacitive-load power consumption (PL).
References:
1. D. A. Pucknell and K. Eshraghian, “Basic VLSI Design: Systems and Circuits”, PHI, 3rd Ed.,1994.
2. W.Wolf, Modern VLSI Design: System on Chip, Third Edition, Pearson, 2002.