Unit-1

Small Signal Amplifiers

1.1 CB, CE, CC configurations

Common Base Configuration

• The notation and symbols of pnp and npn transistors are given below:

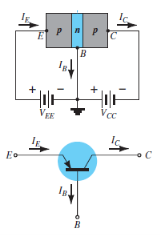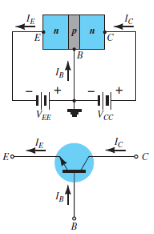Fig. 1: PNP CB and NPN CB (Ref. 2)

• Here the base is common to both the input and output sides of the configuration.
• The flow of holes will govern the direction of current.
• Hence, Ic = Ib + Ie

Where Ic, Ib, Ie are the collector, base and emitter currents respectively.

• The graphical symbol of the PNP common base configuration is

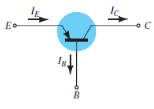Fig. 2: PNP common base (Ref. 2)

• The arrow in the above symbol shows the direction of emitter current in the device.
• Now, to study the behaviour of the device we require two characteristics:

Input Characteristic Curve

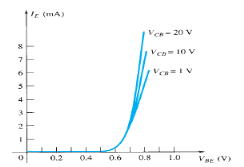Fig.3:  Input Characteristic Curve (Ref. 2)

• It is the relation between the input current IE to the input voltage VBE for various levels of output voltage VCB.
• It is also known as driving point characteristics.

Output Characteristic Curve

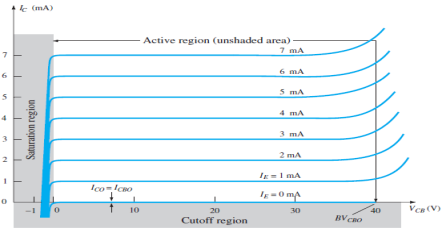Fig.4: Output Characteristic Curve (Ref. 2)

• It is the relation between the output current IC to the output voltage VCB for various levels of input current IE.
• It is also known as collector set of characteristics.
• It has three basic regions:

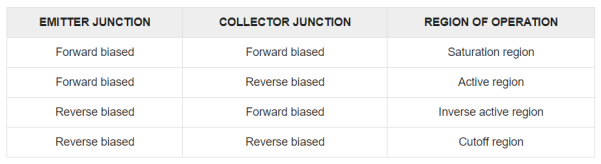
1. Active Region

• Here, base-emitter junction is forward biased and collector-base junction is reverse biased.
• As input current IE increases above zero, output current IC increases to a magnitude equal to IE as determined by the basic transistor current relationship.
• So the first approximation determined by the curve is

IC  ≈  IE

2.     Cut-off Region

• It is defined as the region where the collector current IC is equal to 0A.
• Here, the base-emitter junction and the collector-base junction both are in reverse bias.

3.     Saturation Region

• It is the region that lies towards the left of VCB = 0V.
• Here, the base-emitter junction and the collector-base junction both are in forward bias.

Common Emitter Configuration

• The notation and symbols of npn and pnp transistors are given below:

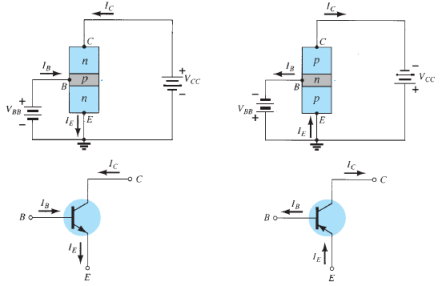Fig. 5: NPN CE and PNP CE (Ref. 2)

• In the above figure all the currents are shown in their actual conventional directions.
• The current relation developed earlier is still applicable,

                  IE = IB + IC

Where IE , IB , IC are the collector, base and emitter currents respectively.

• The graphical symbol of the PNP common emitter configuration is

Fig.6: PNP common emitter (Ref. 2)

• Now, to study the behaviour of the device we require two characteristics:

Input Characteristic Curve

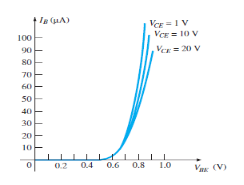Fig.7:  Input Characteristic Curve (Ref. 2)

• It is the graph between the input current IB to the input voltage VBE for a range of values of output voltage VCE.
• Note that the magnitude IB of is in micro amperes and that of IC is in milli amperes.

Output Characteristic Curve

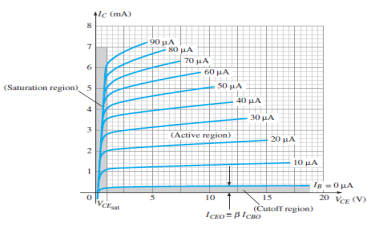Fig.8:  Output Characteristic Curve (Ref. 2)

• It is the graph between the output current IC to the output voltage VCE for a range of values of input current IB.
• It has three basic regions:

Active Region

• Here, the base-emitter junction is forward biased and collector base junction is reverse biased.
• These are the same conditions that existed in the active region of the common base configuration.
• This can be employed for voltage, current or power amplification.

Cut-off Region

• Here IC is not equal to zero when IB is zero.
• For linear amplification purposes, it is defined as IC = ICEO .
• The region below IB = 0µA is to be avoided for undistorted output signal.
• When the transistor is used as a switch, the condition should be ideally IC = 0mA for a chosen VCE voltage.

Saturation Region

• It is the region that lies towards the left of VCE = 0V.

Common Collector Configuration

• The notation and symbols of npn and pnp transistors are given below:

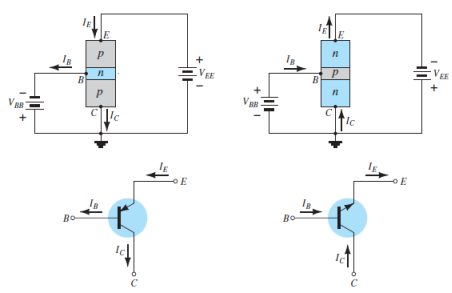Fig. 9: NPN CC and PNP CC (Ref. 2)

• In the above figure all the currents are shown in their actual conventional directions.
• It is used for impedence matching purposes as it has high input impedence and low output impedence.
• It can be designed using common emitter characteristics.
• The output characteristics of common collector is same as that of common emitter configuration for all practical purposes.
• The output characteristics are a plot between  IE versus VCE for all values of IB.
• The input current of common collector is same as that of common emitter configuration.
• Here the region of operation will ensure that maximum ratings are not being exceeded and output ratings have minimum distortion.

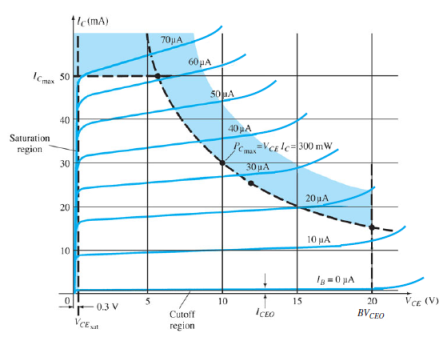Fig.10:  Output Characteristic Curve (Ref. 2)

• The characteristics specifying the minimum VCE that can be applied without entering the non-linear region is saturation region.
• The maximum power dissipation is given by,

P = VCE . IC

Key takeaway

Q1) In a CB IE= 2mA, IC=1.5mA. Calculate IB?

Sol: IE =IB+IC

2= IB+1.5

IB=0.5mA

Q2) In a CB current amplification factor is 0.9. If emitter current is 1.2mA. Determine the value of base current?

Sol: α = 0.9

IE =1.2mA

α = IC/ IE

IC = α IE =0.9 x 1.2 = 1.08mA

IE =IB+IC

1.2= IB+1.08

IB= 0.12mA

Q3) In a CB connection IC=1.0mA and IB= 0.02mA. Find the value of current amplification factor?

Sol: IE =IB+IC =1+0.02 = 1.02mA

α = IC/ IE

α = 1.0/1.02 = 0.98

Q4) In a CB connection the emitter current is 0.98mA. If the emitter circuit is open the collector current becomes 40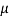A. Find total collector current. α =0.92

Sol: ICBO=40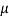A

IC = α IE+ICBO

    = (0.92 x 0.98x10-3) + 40x10-6

IC =0.94mA

Q5) In a common base connection, α = 0.95. The voltage drop across 3 kΩ resistance which is connected in the collector is 2.5 V. Find the base current.

Sol: IC = 2.5/3000 = 0.83mA

α = IC/ IE

IE = IC/α =0.83/0.95=0.87mA

IE =IB+IC

0.87 =IB+0.83

IB=0.04mA

Q6) Find the value of β if (i) α = 0.9 (ii) α = 0.98 (iii) α = 0.99.

Sol: 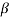= α/1- α = 0.9/1-0.9 = 9

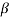= α/1- α = 0.98/1-0.98 = 49

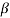= α/1- α = 0.99/1-0.99 = 99

Q7) The collector leakage current in a transistor is 200 μA in CE arrangement. If now the transistor is connected in CB arrangement, what will be the leakage current? Given that β = 120.

Sol: ICEO=200 μA

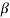= 120

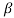α = /1+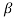= 120/121=0.99

ICEO=ICBO/1- α

ICBO= 1.6 μA

Q8) For a certain transistor, IB = 18 μA; IC = 2 mA and β = 60. Calculate ICBO.

Sol: IC = 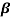IB+ICEO

ICEO= IC - 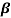IB= 2x10-3-(60x18x10-6) = 0.92mA

α =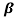 /1+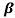= 60/61=0.98

ICBO= (1- α) ICEO = (1-0.98)x 0.92=15.08 μA

1.2 Hybrid model for transistor at low frequencies

The hybrid two port model is shown below.

Fig 11 Hybrid model of transistor

Vi = h11Ii + h12Vo

Io = h21Ii + h22Vo

h11 = hi = Vi/Io for Vo =0  [Input resistance]

h12 = hr = Vi/Vo for Ii =0  [Reverse voltage gain]

h21 = hf = Io/Ii for Vo =0   [forward current gain]

h22 = ho = Io/Vo for Ii =0   [output admittance]

The hybrid equivalent model is shown below

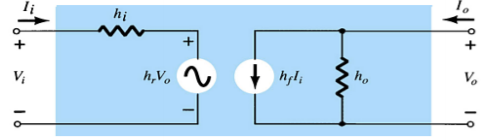Fig 12 hybrid equivalent mode

The transistor model has three terminals with two ports.

hi = input resistance

ho= output conductance

hr= Vi/Vo = reverse transfer voltage

hf= Io/Ii = forward transfer current ratio

The simplified model is shown below

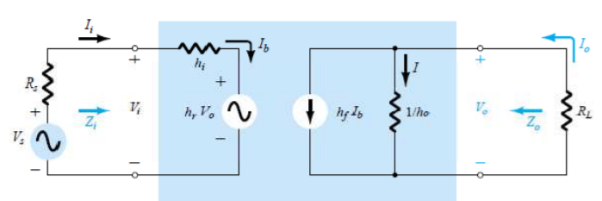Fig 13 Simplified model

Finding current gain Ai

Applying KCL at the output of above circuit

Io =I + hf Ib = Vo ho + hf Ib

Vo = -Io RL

Io = -Io RL ho + hf Ib

Io (1 + RL ho) = hf Ib

Ai = Io/ Ib = hf/(1 + RL ho)

Finding Voltage Gain AV

Applying KVL at input of the above h-model

Vi = hi Ib + hr Vo

But Ib = (1 + ho RL)/hf

Io = - Vo/RL

Substituting in above equation and solving for Vo/Vi­­ we get

Av = - hf RL/hi + (hi ho- hf hr) RL

Finding Input Impedance Zi

Vi = hi Ib + hr Vo

Io = - Vo/RL

Ai = Io/ Ib

Vi = hi Ib - hrRLAiIb

Zi = Vi/Ib = hi - hrRLAi

Finding Output impedance Zo

It is ratio of output voltage to output current with Vs =0

Io = Voho + hfIb

Ii = -hrVo/Rs + hi

Zo = Vo/Io = 1/[ho – (hfhr/hi+ Rs)]

Key takeaway

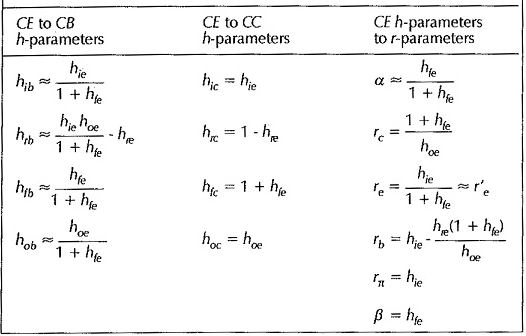
Table of hybrid parameters for CE, CB and CC

1.3 RC coupled amplifiers

It is used for voltage amplification. There are two capacitors one is coupling capacitor Cc connected to output of first stage and base of second stage. The resistances R1, R2 and RE are biasing and stabilisation network. The capacitor CC blocks DC signal and transmits AC signals.

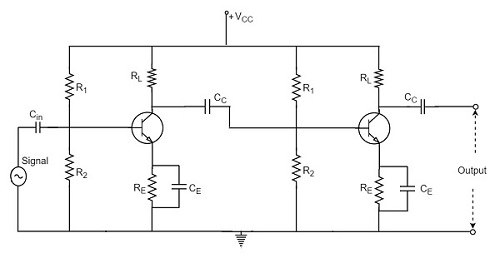Fig 14 RC Coupled Amplifier

When AC signal is applied to base of first transistor it is amplified and appears across its collector Rc. This signal id fed to base of next stage. The second stage amplifies the signal and is received through RL.

Frequency Response: At low frequency the reactance of CC is high and hence very small part of signal passes from first stage to second. At high frequency the reactance of CC is small and it behaves as short circuit. The capacitive reactance of base-emitter junction is low and causes decrease in current amplification factor 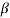. At mid-frequency the voltage gain is constant. As frequency increases gain increases as reactance of CC decreases. This result is higher loading effect of first stage to the next and hence gain decreases. These two factors cancel each other and result in uniform gain.

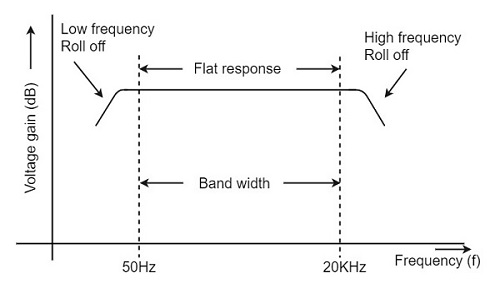Fig 15 Frequency Response of RC coupled Amplifier

Key takeaway

It is used for voltage amplification. There are two capacitors one is coupling capacitor Cc connected to output of first stage and base of second stage. At low frequency the reactance of CC is high and hence very small part of signal passes from first stage to second. At high frequency the reactance of CC is small and it behaves as short circuit. The capacitive reactance of base-emitter junction is low and causes decrease in current amplification factor .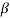

1.4 Mid band model, gain and impedance

The mid band gain of transistor is the transistors gain at its mid frequencies where the transistors gain is at the highest.

The mid band gain is the most important region of transistor amplification. This is because this is the region of frequencies where a transistor produces a constant and high level of gain. When a transistor is rated for its gain or amplification factor, it is the mid band region that this is referring to.

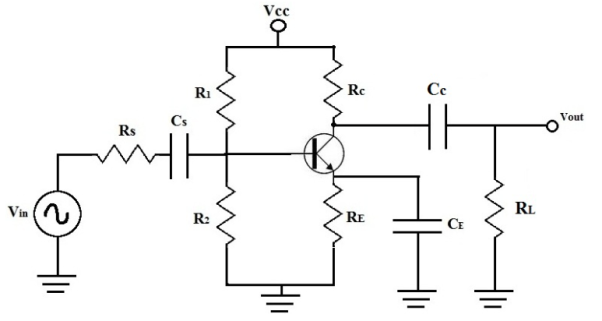Fig 16 Transistor for mid band gain 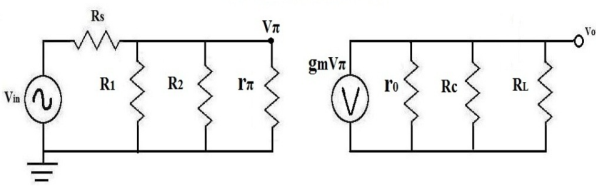Fig 17 AC equivalent Circuit of transistor for mid band gain

The mid band gain of the transistor circuit is

AM = Vout/Vin

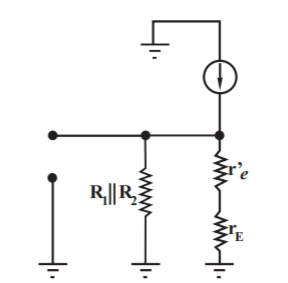
Let us consider the below circuit.

Now calculating the impedance

RB = R1||R2 = [(R1+R2)/R1R2]

Now the value of resistance RB’ is

RB’ = RB||r= [(RB r)/ RB r]

The value of output resistance RL’

RL’ = r0||Rc||RL

The value of voltage drops across r is

V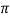 = [RB’Vin/(RB’+RS)]

The reduced circuit now can be redrawn as

Fig 18 Reduced Equivalent Circuit

Vout = -gm V RL’= - gm RL’[RB’Vin/(RB’+RS)]

The mid-band gain is given as

AM= Vout/Vin = - gm RL’[RB’Vin/(RB’+RS)]/Vin

AM= - gm RL’[RB’/(RB’+RS)]

Key takeaway

The value of output resistance RL’

RL’ = r0||Rc||RL

The value of voltage drops across r is

V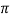 = [RB’Vin/(RB’+RS)]

The mid-band gain is given as

AM= - gm RL’[RB’/(RB’+RS)]

1.5 Comparisons of different configurations

1.6 Emitter follower, Darlington pair (derive voltage gain, current gain, input and output impedance).

1.6.1 Emitter Follower

This is also called as common collector amplifier. It is basically used to provide current gain and for impedance matching. The circuit is shown below where the input is applied through base and output is obtained from emitter. The voltage gain is always<1 and output voltage are in phase with input voltage. The output follows the input hence it is called as emitter follower.

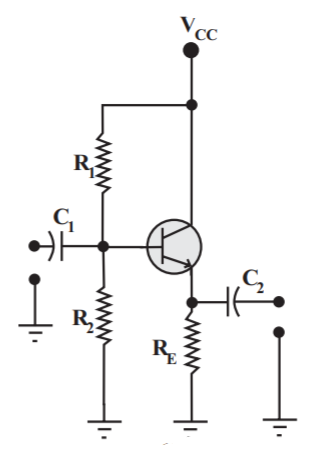Fig 19 Emitter Follower

The base voltage can be obtained by applying voltage division rule on R2 and R1

VB =   VCC

The emitter voltage is VE = VB – 0.7

The emitter current is IE =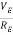

VCEQ = VCC-VE

For A.C analysis the circuit can be drawn as shown below

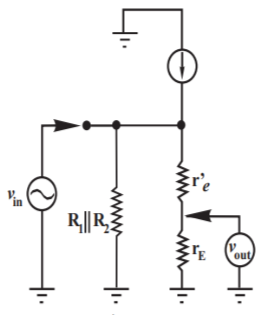
Fig 20 A.C equivalent circuit

The total equivalent ac emitter resistance is rE which is

rE = RE||RL

• The voltage gain AV = rE/(re’ +rE)

Practically re’ << rE. The voltage gain then becomes

AV = 1

• Current Gain Ai = hfe (Zin rE/Zbase RL)

This relationship is due to the current divisions that occur in both the input and output circuits. We have used in place of hfe. We are assuming that is approximately equal to hfe. The subscript “c” merely indicates that the parameter applies to the emitter follower (common collector) rather than the common emitter amplifier. The exact equation for hfc is

hfc = hfe +1

Since is normally much greater than 1, we normally assume that they are approximately equal.

• Input Impedance Zin = R1||R2||Zbase
• Base Input Impedance Zbase = hfe (re’+rE)

Where:

hfe= transistor current gain

re’= the ac emitter resistance

rE = RL||RE

• Output Impedance (Zout)

The output impedance is the impedance that the circuit presents to its load. When a load is connected to the circuit, the output impedance of the circuit acts as the source impedance for that load.

Zout = RE|| [re’ + (Rin’/hfe)]

1.6.2 Darlington Pair –

The Darlington pair is a combination of two common collector cascade configuration. In Darlington pair the collectors of the two transistors are connected together, emitter of Q1 is connected to the base of Q2 and emitter of Q2 acts as the emitter of Darlington connection.

The important feature of the Darlington connection is that the composite will act as a single unit, the current gain of which is equal to the product of the individual current gains β1 and β2 .

Fig 21: Darlington connection of transistors

In general Darlington connection with more than 2 transistors is not used because

1)     With increase in transistors, leakage current increases.

2)     The voltage gain of CC is approximately 1 but that of the Darlington is much less than 1. With increase in transistor, voltage gain will decrease further.

Advantages:

1)     Very high current gain.

2)     Very low voltage gain.

3)     Very high input impendence.

4)     Very low output impendence.

Disadvantage – more than 2 transistors cannot be used.

Analysis of Darlington emitter follower –

The circuit diagram of the Darlington emitter follower is shown above.

Assumptions –

1)     Both Q1 and Q2 are identical.

2)     hoe 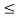0.1 i.e. approximate analysis.

3)     hfe RE >> hie

1.Current gain of the Darlington emitter follower (AI):

a)     current gain  of Q2 :

AI2 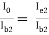= (1 + hfe)

b)    current gain of Q1 :

The input resistance of stage 2 acts as the load for Q1

Ri2 = hie + (1 + hfe)RL2

         = hie + AI2RE            {where RL2 = RE}

As Ri2 is large, the condition hoe RL’ < 0.1 is not satisfied by first stage

Where RL’ = RL2 = RE

Hence using exact analysis for Q1

AI1 =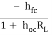

Substitute 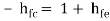and , we get

AI1 = 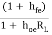                 -------------(1)

But 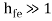hence, RL1 = Ri2 = hie + hfeRE

Substituting the expression for RL1 in equation (1)

AI1 =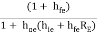

hoehie is very small so neglecting it,

AI1 =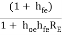

Overall current gain :  AI =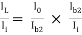

i.e. AI = AI1 AI2

           =

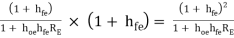
AI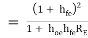              -------------(2)

The above equation shows that overall current gain of the Darlington connection is much higher than that of the single  emitter follower (common collector).

2.Overall input resistance (Ri) :

The overall input resistance will be same as the input resistance of first stage Q1

Ri = Ri1

Ri1 = hie + AI1RL1     where  RL1 = Ri2

Substituting the value of AI1 and Ri2, we get

Ri1 = hie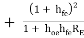RE                       --------------(3)

2nd term in equation (3) is much larger than first term, so neglecting hie

Input resistance, Ri1 =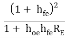RE   

If hoehfeRE << 1, then

Ri1 =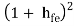RE        ----------------(4)

For a single CC amplifier Ri = hi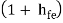e + RE

Equation (4) shows that due to Darlington connection, there is tremendous increase in input resistance.

3.Voltage Gain of Darlington connection (AV) :

Overall voltage gain AV =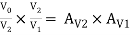

AV2 is calculated using approximate analysis.

AV1 is obtained by exact analysis.

a)     Voltage gain AV2 =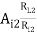

AI2 = 1 + hfe

Ri2 = hie + (1 + hfe)RL2

RL2 = RE

                                                                            {Adding and subtracting hie in numerator}

AV2 = 1 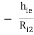            ----------(5)

b)    Voltage gain AV1: AV1 = AI1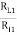

But for single emitter follower,

AI1 = (1 + hFe),

Ri1 = hie + AI1RL1

AV1 = 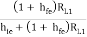   where RL1 = Ri2

Adding and subtracting hie in numerator of right-hand side, we get

AV1 =

AV1 = 1 -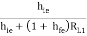

AV1 = 1 - 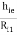              -----------(6)

Overall voltage gain = AV = AV1 × AV2

i.e. AV = AV2 =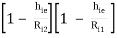 

AV =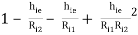 

It is evident that Ri1 >> Ri2 hence 3rd and 4th term in above equation can be neglected

AV = 1 -                              -------------(7)

Comparing (5) and (7)

AV 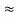AV2

The overall voltage gain is approximately equal to the voltage gain of second stage.

4.Overall output resistance RO :

The overall output resistance of the emitter follower Darlington circuit is same as the output resistance of second stage.

YO = hoc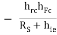

Hence  YO2 = hOC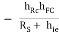

Hence YO2 = hOC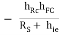

RS for 2nd stage is R01 i.e. output resistance of 1st stage.

But hrc = 1 , hOC = hOe , hFC = - (1 + hFe)  and hiC = hie

YO2 = hoe +

Neglect hOe because we are performing approximate analysis for the second stage we get,

YO2 =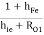

Hence, RO2 =

But, RO1 =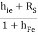

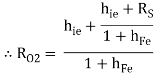
RO = RO2 = +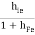

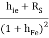
Neglect the 2nd term due to in denominator

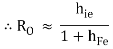
The above equation tells us that the RO of Darlington emitter follower is much less than that of a single emitter follower.

Key takeaway

For emitter follower

The value of Z is typically higher than the common emitter amplifier. The voltage gain is always less than 1 The heavy swamping of the circuit virtually eliminates the effect of r’ on the voltage gain.

Que. For T1  hie1 = 6 KΩ     hFe1 = 80       hre1 = hoe1 = 0

             For T2  hie2 = 1 KΩ     hFe2 = 100     hre2 = hoe2 = 0

             For the Darlington pair emitter follower, shown in figure, determine:

a)     Input impendence R1                      

b)    Voltage gain  VO / VS

c)     Current gain IO / IS

d)    Output impendence

Sol – Given: hie1 = 6 KΩ     hFe1 = 80       hre1 = hoe1 = 0

                       hie2 = 1 KΩ     hFe2 = 100     hre2 = hoe2 = 0

Amplifier configuration:

Q1 → CC           Q2 → CC

Therefore, approximate analysis is used, for both stages

For second stage:

Current gain (Ai2)

AI2 = 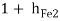= 1 + 100 = 101

Input resistance (Ri2)

RL1 = Ri2 = hie2 + (1 + hFe2)RL = 1 × 103 + (1 + 100) × 103 = 102 KΩ

Voltage gain (AV2):

AV2 = 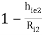=1 - 0.99

For first stage:

Current gain (Ai1):

Ai1 = 1 + hFe1 = 81

Input resistance (Ri1):

Ri1 = hie1 + (1 + hFe1 )RL

      = 6 × 103 + (1 + 80) × 102 × 103 = 8.268 MΩ

Voltage gain (AV1):

AV1 = = 1 - 0.999

RO1 = 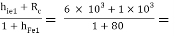86.42 Ω

RO2 =  10.76 Ω

Overall voltage gain (AV):

AV = AV1 × AV2 = 0.999 × 0.99 = 0.989

AVS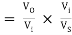

Figure shows equivalent circuit of the input side

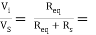0.998

AVS = 0.989 × 0.998 = 0.987

Overall voltage gain:

AI = Ai = Ai1 × Ai2 = 81 × 101 = 8181                      Ans.

Input impendence:

Ri = 0.89 MΩ                                                            Ans.

Overall voltage gain:

AV = 0.989                                                                 Ans.

Voltage gain include source:

AVS = 0.987                                                               Ans.

Output Impendence:

RO = 10.76 Ω                                                             Ans.

Que. For the bootstrap circuit shown, calculate AI , Ri and AV. The transistor parameters are hie = 2 KΩ , hFe = 100 , = 40 K and hre = 2.5 × 10-4.

Sol – Given  : hie = 2 KΩ , hFe = 100 , 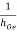= 40 K , hre = 2.5 × 10-4.

Amplifier configuration : common emitter with Re

AC analysis : For a.c. Analysis of amplifier we consider the d.c. Supply voltage as ground and capacitor as short circuit and apply Miller’s theorem across feedback resistor (10K)  then modified circuit is given as :

The circuit down in fig. (a) represents a CE amplifier. But to analyse the bootstrapped element we need to consider the CC voltage gain first.

AV = 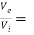common collector voltage gain

RL’ = 2K || 4K || 4K || 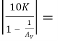1 K || 490 K = 1 KΩ

Assume AV 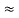0.98

Checking approximation :

hoeRL’ 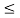0.1

0.025 < 0.1

Hence , valid approximation

Approximate analysis :

AI = 1 + hFe = 101

Ri = hie + (1 + hFe)RL’ = 2 + 101 = 103 KΩ             Ans.

AV = AI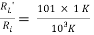= 0.98

From fig. (a) : R1 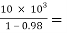 500 KΩ

Now, fig. (a) can be analysed by CE and the modified circuit is given as,

Checking approximation :

hoe (Re + RL) 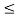0.1

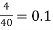
Hence, valid approximation

Approximate analysis :

AI’= 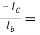-hFe = -100

Ri’= hie + (1 + hFe)Re’ = 2 + 101 × 1 = 103 KΩ

AV’ =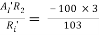

AV = AV’ = -2.9126

From fig. (b) : Ri = Ri’ || 500K = 100 || 500 = 85.406 KΩ

AI =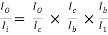

    = (-1) × 100 ×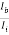

From fig. (c) : - 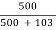= 0.8291

Hence, AI = - 100 × 0.82918 = -82.918

Que. The bootstrapped Darlington pair uses identical transistors with the following h-parameters.

hie = 1 KΩ  , hre = 2.5 × 10-4 , hoe = 2.5 × 10-4 A/V , hFe = 100

Find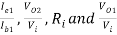

Sol - Given  : hie = 1 KΩ  , hre = 2.5 × 10-4 , hoe = 2.5 × 10-4 A/V , hFe = 100

Q1 – CC , Q2 - CC

For a.c. Analysis of amplifier we consider the d.c. supply voltage as ground and capacitor as short circuit.

Apply Miller’s theorem across R3 = (100K)

Voltage Gain :

AV = 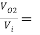AV1 × AV2

Let us assume AV = 0.98

Where , 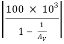= 4900 KΩ

RL’ = 0.1K || 82K || 10K || 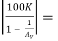0.1 K || 82 K || 10 K || 4900 K  = 0.0988 KΩ

Analysis for Q2 [CC] :

Checking approximation :

hoeRL’ = 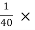0.0988 = 2.47 × 10-3 < 0.1

Approximate analysis :

AI2 = 1 + hFe = 101

Ri2 = hie + (1 + hFe)RL’ = 1 + 101 × 0.0988 = 10.9788 KΩ          

AV2 = AI2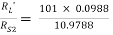= 0.908915

Analysis for Q1 [CC] :

RL = Ri2

hoeRL1 = 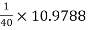= 0.27447 > 0.1

Exact analysis :

AI2 = 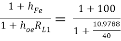= 79.2486

Ri1 = hie + AI1hrcRL1 = 1 + 79.2486 × 10.9788

       = 871.054 KΩ                     (hrc 1)

AV1 =

         = 0.99885

AV 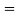AV1 × AV2 = 0.99885 × 0.908915

= 0.9079                                      (Ans)

Ri = R || Ri1 = 1085.78 || 871.054                {Fig. (a)}

        = 483.32 KΩ

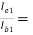AI1 = 79.2486

AI =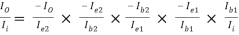

     =

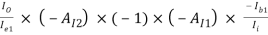
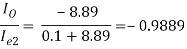
AI = (-0.9889) × (-101) × (-1) × (-79.2486) × 0.55487

    = 4391.94                                (Ans)

Equation for VO/Vi :

Analysis of Q2 [CC] :

hoe(Re+RL)

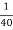×[0.0988 + 1]  = 0.02747 < 0.1

Approximate analysis

AI2 = - hFe =  -100

Ri2 = hie + (1 + hFe)Re

     = 1 +(1 + 100)0.0988 = 10.9788 KΩ

AV2 = = 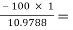-9.1084

Analysis of Q1 [CC] :

RL1 = Ri2 = 10.9788 KΩ

hoeRL1 = 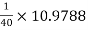 = 0.27447 > 0.1

Exact analysis :

AI1 = = 79.2486

RL1 = hie + AI1RL1 = 1 + 79.2486 × 10.9788

   = 871.054 KΩ

AV1 = =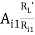

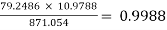
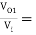AV = AV1 × AV2 = -9.0975

Hence, -AI1 = 79.248

Ri = 483.32 KΩ

-9.0975                                 (Ans)

Que. A bootstrapped Darlington amplifier shown in fig. Uses identical transistor with h-parameters, hie = 1.5 KΩ , hoe = 50 μA/V. If the circuit is to have Ri of 268 MΩ. Find the value of hFe for the transistor used.

Sol – Given  : hie = 1.5 KΩ , hoe = 50 μA/V, Ri = 2.68 MΩ, R1 = 1 MΩ , R2 = 1 MΩ , Re2 = 1 KΩ

RLeft = RC1 || RC2 = ∞ || 1 K = 1 KΩ

Amplifier configuration : bootstrapped Darlington pair amplifier [CC - CC]

Checking for approximation :

hoeRLeft 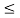0.1

hoeRLeft = 25 × 10-6 × 1 K = 0.025 < 0.1

Which is less than 0.1

Approximate analysis :

Calculation for hFe

Ai2 = 1 + hFe

Ri2 = hie2 + Ai2RLeft = 1.5 K + (1 + hFe)1 K

Ai1= 1 + hFe

Ri1 = hie1 + Ai1RL1

Where RL1 = Ri2

Ri1 = 1.5K + (1 + hFe)[1.5K + (1 + hFe)1K]

2.68 MΩ = 1.5K + 1.5K + (1 + hFe)1K + 1.5Khfe + (1+hFe) 1KhFe

                 = 3K + 1K + 1KhFe + 1.5KhFe + 1KhFe + 1KhFe2

                 = 4K + 3.5KhFe + 1KhFe2

    = (4 + 3.5hFe + hFe2) × 103

hFe2 + 3.5hFe + 4 = 2680

hFe2 + 3.5hFe - 2676 = 0

The quadratic equation can be solved as,

hFe =

Substituting values we get,

hFe

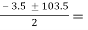       = 50 or -53.5

hFe is always positive.

hFe = 50                                                          Ans.

Overall voltage gain :

(AV) : AV = AV1 × AV2 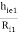= ( 1 - 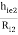)( 1 - )

                                   = ( 1 - )( 1 - )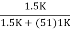

        = 0.999 × 0.971 = 0.97

Overall current gain –

Ai = Ai1 × Ai2

     = (1 + hFe) (1 + hFe)

     = (51)(51)

     = 26.01

Key takeaway

Sr. No.	Parameter	Expression
1	Current gain (AI)	AI
2	Input resistance (Ri)	Ri = 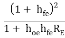RE
3	Voltage gain (AV)	AV = 1 -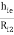
4	Output resistance (RO)	RO = +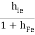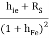

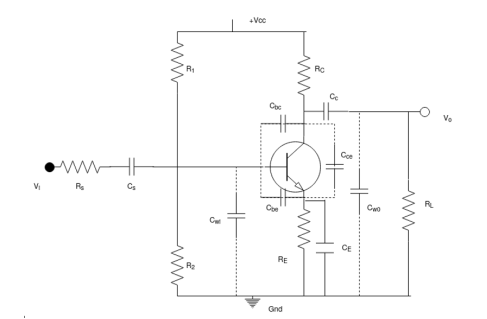1.7 Hybrid-model at high frequencies (pi - model)

Fig 22 Transistor model 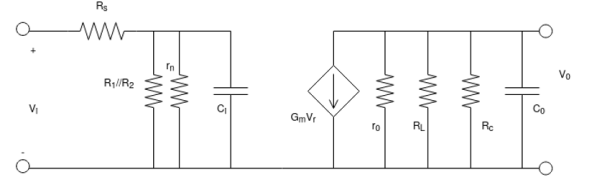Fig 23 Hybrid equivalent pi-model

Ci = cwi + cbe + cbc( 1-av)                                  Co = cwo + cce + cbc( 1-AV)

      = cwi + cbe + cmi = cwo + cce + cmo

Where cmi = input miller capacitance     where cmo = o/p miller capacitance

At increasing frequencies, the reactance xc will decrease in magnitude resulting in a shorting effect across the output and a decrease in gain.

For high frequency response, various parasite capacitances (cbe, cbc, cce) of the transistors are included along with the wiring capacitors ( cwi, cwo) for analysis.

For high frequency response, cs, cc, ce are assumed to be in short circuit state.

Input capacitance ci includes wiring capacitance cwi, the transistor capacitance.

Cbe and miller capacitance cmi.

The o/p capacitance co includes wiring cce and miller capacitance cmo

Cmi = cbc (1-av)

Cmo = cbc (1−11−1/av)

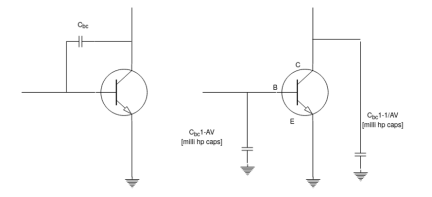
Fig 24 Output capacitance

For the input network, the – 3db frequency is defined by

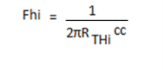
Rthi = rsrs // r1r1 // r2r2 // rππ

Ci = cwi + cbc + cmi

Cmi = cbc (1-av)

At very high frequency, the effect of ci is to reduce the total impedance of the parallel combination of r1r1, r2r2 , rπrπ & ci. The route is a reduced level of voltage across ci, a reduction in In and a gain for the system.

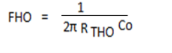
Rtho = rc // rlrl // re

c0c0 = cwot + cce + cmo

Cme = cbe ( 1 - 1av)1av)

∵∵ 1 >> yav cmo = cbc

At very high frequency, XCO will decrease and consequently reduced the total impedance of o/p parallel branches. The net result is vo will also decline towards ‘o’ as the reactance xc becomes (zero) or smaller.

Reference:

1 “Electronic Devices and Circuit Theory”, Boylestad and Nashelsky, PEARSON

PUBLICATION.

2 “Electronic devices and circuits”, Salivahanan, Suresh Kumar, Vallavaraj,

TMH, 1999

3 “Integrated Electronics, Analog and Digital Circuits and Systems”, J. Millman

And Halkias, TMH, 2000

4 “Micro Electronic Circuits”, Sedra and Smith, Oxford University Press, 2000

5 “Electronic Devices and Circuits”, David A Bell, Oxford University Press, 2000