Unit 2

Modulation and Demodulation

2.1 Modulation (upward frequency translation) and demodulation (downward frequency translation) and the need for modulation

Modulation (upward frequency translation)

      It is a process through which audio, video, image or text information is added to an electrical or optical carrier signal that is to be transmitted over a telecommunication or electronic medium.

      It enables the transfer of information on an electrical signal to a receiver that is capable of demodulating the signal to extract the blended information.

1. Amplitude Modulation (AM): Amplitude of the carrier is modulated.
2. Frequency Modulation (FM): Frequency of the carrier is modulated.
3. Phase Modulation (PM): Phase of the carrier is modulated.

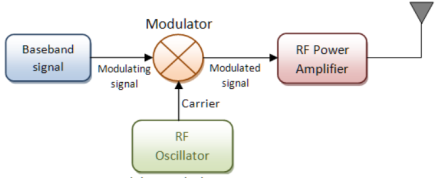
Fig.1: Modulation

Demodulation (downward frequency translation)

      It is the process of extracting the original information-carrying signal from a modulated carrier wave.

      A demodulator is an electronic circuit that is mainly used to recover the information from the modulated carrier wave.

      There are different types of demodulators.

      The output signal via demodulator may be sound, images or binary data.

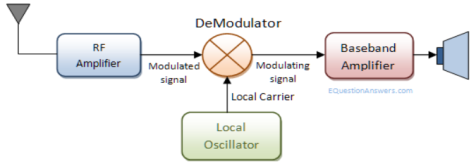
Fig.2: Demodulation

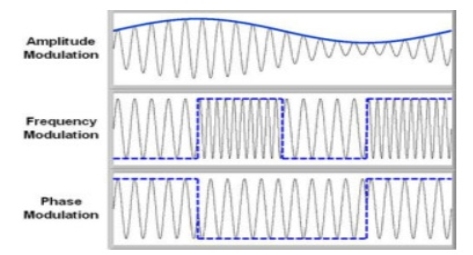
Fig.3: Demodulated Output

Necessity of Modulation: -

1>. Antenna height reduces

2>. Avoids mixing of signal

3>. Increases the range of communication [ In Kilometres]

4>. Multiplexing of signals is possible

5>. Improves quality of reception of signal.

1>. Antenna height Reduces: - Antenna theory specifies that the height of the antenna required for radiation of radio waves is a function of wavelength of the frequency fed at the i/p of the antenna. Antenna height must be multiple of ( d/4 ),

Where ‘ d ‘ is the wavelength.

d = speed of light / frequency of signal

d = c / f = 3 x 108 / f

Eg : Consider the voice as analog baseband signal with f = 4 KHz

d = 3 x 108 / 4 x 103

d = 75 x 103 m

d = 75 km

Height of antenna required is d / 4

= 75 km / 4 = 18.75 km

Q. Practically you cannot build the antenna of 18.7 km height. Consider this voice signal of 4 kHz frequency is used to modulate the carrier signal of 2 MHz frequency.

F = 2 MHz

D = c / f = 3 x 108 / 2 x 106 = 150 m

Minimum height of antenna required = d / 4 = 150 / 4 = 37.5 m

Therefore, antenna height required for radio communication reduces from 75 km to 37.5 meters due to modulation.

2>. Increase range of communication: - The frequency of baseband signal is low. At low frequency the signal radiation from antenna is poor or weak. Due to this reason the signal gets attenuated and can’t travel long distance when it is transmitted.

Attenuation of the transmitted signal reduces when the frequency is increased.

Thus modulation increases the frequency of the signal to be radiated. Thus, increase in frequency increases the range of communication.

Key Takeaways:

1. Modulation increases the frequency of the signal to be radiated.
2. Antenna height must be multiple of ( d/4 ).
3. Demodulation is the process of extracting the original information-carrying signal from a modulated carrier wave.
4. Modulation is a process through which audio, video, image or text information is added to an electrical or optical carrier signal that is to be transmitted over a telecommunication or electronic medium.

2.2 Broad classification of modulation [linear (amplitude-AM) and exponential (frequency-FM and Phase-PM)]

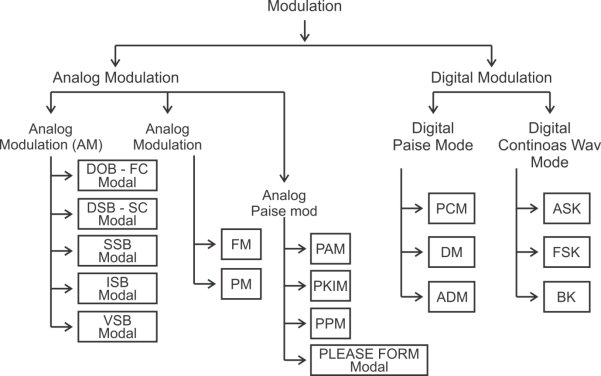
Fig.4: Classification of Modulation

Amplitude Modulation

The amplitude of the carrier signal varies in accordance with the instantaneous amplitude of the modulating signal. That is the amplitude of the carrier signal containing no information varies as per the amplitude of the signal containing information, at each instant.

Consider the following diagram

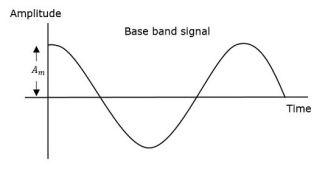
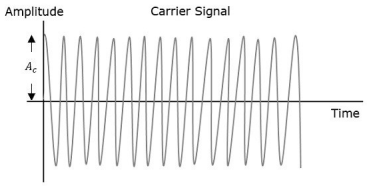
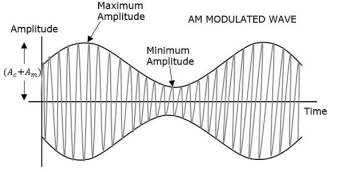
Fig.5 : AM

The first figure shows the modulating wave, which is the message signal. The next one is the carrier wave, which is a high frequency signal and contains no information. While, the last one is the resultant modulated wave.

It can be observed that the positive and negative peaks of the carrier wave are interconnected with an imaginary line. This line helps recreating the exact shape of the modulating signal. This imaginary line on the carrier wave is called as Envelope. It is the same as that of the message signal.

Therefore we can say that Amplitude Modulation is the process of changing the amplitude of a relatively high frequency carrier signal in accordance with the amplitude of the modulating signal (Information). The carrier amplitude varies linearly by the modulating signal  which usually consists of a range of audio frequencies. The frequency of the carrier is not affected.

The various forms of Amplitude Modulation are:

• Conventional Amplitude Modulation Full AM or Double Sideband Large carrier modulation (DSBLC) /Double Sideband Full Carrier (DSBFC)
• Double Sideband Suppressed carrier (DSBSC) modulation.
• Single Sideband (SSB) modulation

Angle Modulation

Another type of modulation in continuous-wave modulation is Angle Modulation.

Angle Modulation is the process in which the frequency or the phase of the carrier

Signal varies according to the message signal.

The standard equation of the angle modulated wave is

s(t)=Ac cosθi(t)-------------------(1)

Where,

Ac is the amplitude of the modulated wave, which is the same as the amplitude of the carrier signal

θi(t) is the angle of the modulated wave

Angle modulation is further divided into frequency modulation and phase modulation.

• Frequency Modulation is the process of varying the frequency of the carrier signal linearly with the message signal.
• Phase Modulation is the process of varying the phase of the carrier signal linearly with the message signal.

Phase Modulation

In frequency modulation, the frequency of the carrier varies whereas, in Phase Modulation (PM), the phase of the carrier signal varies in accordance with the instantaneous amplitude of the modulating signal.

So, in phase modulation, the amplitude and the frequency of the carrier signal remains constant.

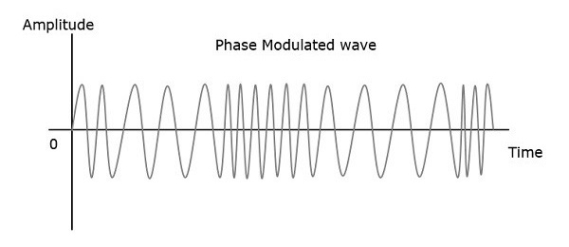
Fig.6: Phase Modulation

The phase of the modulated wave has  infinite points, where the phase shift in a wave can take place. The instantaneous amplitude of the modulating signal changes the phase of the carrier signal. When the amplitude is positive, the phase changes in one direction and if the amplitude is negative, the phase changes in the opposite direction.

Representation

The equation for instantaneous phase ϕi in phase modulation is

ϕi=kpm(t)----------------------(1)

Where,

• Kp is the phase sensitivity
• m(t) is the message signal

The standard equation of angle modulated wave is

s(t)=Ac cos(2πfct+ϕi)---------------------------------(2)

Substitute, ϕi value in the above equation.

s(t)=Ac cos(2πfct+kpm(t))-----------------------------------(3)

This is the equation of PM wave.

If the modulating signal, 

m(t)=Am cos(2πfmt)--------------------------------(4)

Then the equation of PM wave will be

s(t)=Ac cos(2πfct+βcos(2πfmt))-----------------------------------(5)

Where,

• β = modulation index = Δϕ=kpAm
• Δϕ is phase deviation

Phase modulation is used in mobile communication systems, while frequency modulation is used mainly for FM broadcasting.

Bessel Function and its Mathematical Analysis

Time – Domain Expression:

Since the FM wave is a nonlinear function of the modulating wave, the frequency modulation is a nonlinear process.

Let us consider a single-tone sinusoidal message signal defined by

n(t) = An cos(2nƒnt) -----------------------(1)

The instantaneous frequency is

ƒ(t) = ƒc+kƒAn cos(2nƒnt) -----------------------(2)

= ƒc+∆ƒ cos(2nƒnt)-----------------------------(3)

∆ƒ = kƒAn

= 2 πfct + 2πKf 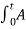m cos(2 πfmt) dt -------------------(4)

= 2 πfct + 2πKf  Am / 2πfm sin(2πfmt)  --------------------(5)

= 2 πfct + Kf  Am/fm sin(2πfmt)  ------------------------(6)

= 2 πfct + β f sin(2πfmt) ---------------------------(7)

Where  β = ∆ƒ/fm = Kf  Am/fm = modulation index.

Therefore, the single-tone FM wave is expressed by

FM(t) = Ac cos[2nƒct + þƒ sin(2nƒnt)] ------------------------------(8)

This isthe desired time-domain expression of the single-tone FM wave

Similarly, single-tone phase modulated wave may be determined where

PM(t) = Ac cos[2nƒct + kp An cos(2nƒnt)] -------------------------(9)

Or, PM(t) = Ac cos[2nƒct +þp cos(2nƒnt)] --------------------------(10)

þp = kpAn ---------------------------(11)

The frequency deviation of the single-tone PM wave is

FM(t) = Ac cos[2 πfct + β f sin(2πfmt)]-----------------(12)

Frequency Modulation

In amplitude modulation, the amplitude of the carrier signal varies, whereas in Frequency Modulation (FM), the frequency of the carrier signal varies in accordance with the instantaneous amplitude of the modulating signal.

Hence, in frequency modulation, the amplitude and the phase of the carrier signal remains constant.

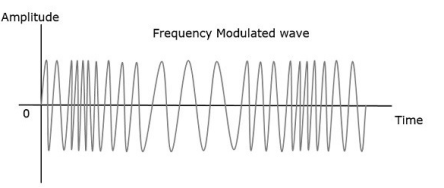
Fig.7: Frequency Modulation

• The frequency fi of the information signal controls the rate at which the carrier frequency increases and decreases. As with AM, fi must be less than fc. The amplitude of the carrier remains constant throughout this process.
• When the information voltage reaches its maximum value then the change in frequency of the carrier will have also reached its maximum deviation above the nominal value.
• Similarly, when the information reaches a minimum the carrier will be at its lowest frequency below the nominal carrier frequency value.
• When the information signal is zero, then no deviation of the carrier will occur. The maximum change that can occur to the carrier from its base value fc is called the fc. This sets the dynamic range i.e. voltage frequency deviation, of the transmission. The dynamic range is the ratio of the largest and smallest analogue information signals that can be transmitted.

Representation:

The equation for instantaneous frequency fi in FM modulation is

Fi=fc+kfm(t)------------------------(1)

Where,

Fc is the carrier frequency

Kt is the frequency sensitivity

m(t) is the message signal

We know the relationship between angular frequency ωi and angle θi(t) as

ωi=dθi(t)/dt -------------------------(2)

2πfi=dθi(t)dt-------------------------(3)

θi(t)=2π 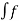i dt -------------------------(4)

Substitute, fi value in the above equation.

θi(t)=2π 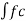+k fm(t))dt-----------------(5)

θi(t)=2πfct+2πkf 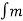(t)dt --------------------(6)

This is the equation of FM wave.

If the modulating signal is m(t)=Am cos(2πfmt)  then the equation of FM wave will be

s(t)=Ac cos(2πfct+βsin(2πfmt))-------------------(1)

Where,

β = modulation index =Δf/fm=kfAm/fm----------------------(2)

The difference between FM modulated frequency which is the instantaneous frequency and normal carrier frequency is termed as Frequency Deviation. It is denoted by Δf which is equal to the product of kf and Am.

FM can be divided into Narrowband FM and Wideband FM based on the values of modulation index β.

Key Takeaways:

1. In amplitude modulation, the amplitude of the carrier signal varies, whereas in Frequency Modulation (FM), the frequency of the carrier signal varies in accordance with the instantaneous amplitude of the modulating signal.
2. In frequency modulation, the frequency of the carrier varies whereas, in Phase Modulation (PM), the phase of the carrier signal varies in accordance with the instantaneous amplitude of the modulating signal.

References:-

1. “Electronic communication system”, by Kennedy, TMH
2. “Communication system”, by haykin wiley
3. “Communication system”, by bruce carison, TMH
4. “Modern digital and analog communication”, B.P. LATHI, Oxford