Unit 2
Boolean laws and theorems
- It deals with binary numbers & variables.
- Therefore, also known as Binary Algebra or logical Algebra.
- A mathematician named as George Boole had developed this algebra in 1854.
- The variables that are used in this algebra are known as Boolean variables.
- Considering the range of voltages as logic ‘High’ is represented with ‘1’ and logic ‘Low’ is represented with ‘0’.
Boolean Postulates
- Considering the binary numbers 0 and 1, boolean variable (x) and its complement (x’).
- They known as literal.
- The possible logical OR operations are:
x + 0 = x
x + 1 = 1
x + x = x
x + x’ = 1
- Similarly, the possible logical AND operations are:
x.1 = x
x.0 = 0
x.x = x
x.x’ = 0
- These are the simple Boolean postulates and verification can be done by substituting the Boolean variable with ‘0’ or ‘1’.
Key Takeaways:
- The range of voltages as logic ‘High’ is represented with ‘1’ and logic ‘Low’ is represented with ‘0’.
- Logical OR is summing of the literals and logical AND is multiplication of the two literals.
- Digital electronic circuits operate at two logic levels namely Logic Low and Logic High.
- The Logic Low is represented with ‘0’and Logic High is represented with ‘1’.
- The basic digital electronic circuit which has one or more inputs and single output is known as Logic gate.
- These Logic gates are known as the building blocks of any digital system. They can classified as:
Basic gates
Universal gates
Special gates
Basic Gates
The basic gates are namely AND gate, OR gate & NOT gate.
AND gate
It is a digital circuit that consists of two or more inputs and a single output which is the logical AND of all those inputs. It is represented with the symbol ‘.’.
The following is the truth table of 2-input AND gate.
A | B | Y = A.B |
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Here A, B are the inputs and Y is the output of two input AND gate.
If both inputs are ‘1’, then only the output, Y is ‘1’. For remaining combinations of inputs, the output, Y is ‘0’.
The figure below shows the symbol of an AND gate, which is having two inputs A, B and one output, Y.

Fig.1 : AND gate (ref. 1)
OR gate
It is a digital circuit which has two or more inputs and a single output which is the logical OR of all those inputs. It is represented with the symbol ‘+’.
The truth table of 2-input OR gate is:
A | B | Y = A + B |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 1 |
Here A, B are the inputs and Y is the output of two input OR gate.
When both inputs are ‘0’, then only the output, Y is ‘0’. For remaining combinations of inputs, the output, Y is ‘1’.
The figure below shows the symbol of an OR gate, which is having two inputs A, B and one output, Y.
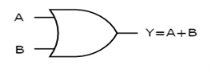
Fig.2 : OR gate (ref. 1)
NOT gate
It is a digital circuit that has one input and one output. Here the output is the logical inversion of input. Hence, it is also called as an inverter.
The truth table of NOT gate is:
A | Y = A’ |
0 | 1 |
1 | 0 |
Here A and Y are the corresponding input and output of NOT gate. When A is ‘0’, then, Y is ‘1’. Similarly, when, A is ‘1’, then, Y is ‘0’.
The figure below shows the symbol of NOT gate, which has one input, A and one output, Y.
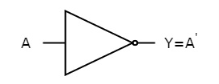
Fig.3 : NOT gate (ref. 1)
Universal gates
NAND & NOR gates are known as universal gates.
We can implement any Boolean function by using NAND gates and NOR gates alone.
NAND gate
It is a digital circuit which has two or more inputs and single output and it is the inversion of logical AND gate.
The truth table of 2-input NAND gate is:
A | B | Y = (A.B)’ |
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Here A, B are the inputs and Y is the output of two input NAND gate. When both inputs are ‘1’, then the output, Y is ‘0’. If at least one of the input is zero, then the output, Y is ‘1’. This is just the inverse of AND operation.
The image shows the symbol of NAND gate:
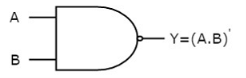
Fig.4 : NAND gate (ref. 1)
NAND gate works same as AND gate followed by an inverter.
NOR gate
It is a digital circuit that has two or more inputs and a single output which is the inversion of logical OR of all inputs.
The truth table of 2-input NOR gate is:
A | B | Y = (A+B)’ |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 0 |
Here A and B are the two inputs and Y is the output. If both inputs are ‘0’, then the output is ‘1’. If any one of the input is ‘1’, then the output is ‘0’. This is exactly opposite to two input OR gate operation.
The symbol of NOR gate is:
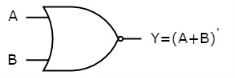
Fig.4 : NAND gate (ref. 1)
NOR gate works exactly same as that of OR gate followed by an inverter.
Special Gates
Ex-OR gate
It stands for Exclusive-OR gate. Its function varies when the inputs have even number of ones.
The truth table of 2-input Ex-OR gate is:
A | B | Y = A⊕B |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Here A, B are the inputs and Y is the output of two input Ex-OR gate. The output (Y) is zero instead of one when both the inputs are one.
Therefore, the output of Ex-OR gate is ‘1’, when only one of the two inputs is ‘1’. And it is zero, when both inputs are same.
The symbol of Ex-OR gate is as follows:
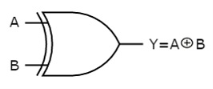
Fig.4 : XOR gate (ref. 1)
It is similar to that of OR gate with an exception for few combination(s) of inputs. Hence, the output is also known as an odd function.
Ex-NOR gate
It stands for Exclusive-NOR gate. Its function is same as that of NOR gate except when the inputs having even number of ones.
The truth table of 2-input Ex-NOR gate is:
A | B | Y = A⊙B |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Here A, B are the inputs and Y is the output. It is same as Ex-NOR gate with the only modification in the fourth row. The output is 1 instead of 0, when both the inputs are one.
Hence the output of Ex-NOR gate is ‘1’, when both inputs are same and 0, when both the inputs are different.
The symbol of Ex-NOR gate is:
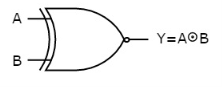
Fig.5 : XNOR gate (ref. 1)
It is similar to NOR gate except for few combination(s) of inputs. Here the output is ‘1’, when even number of 1 is present at the inputs. Hence is also called as an even function.
Basic Laws of Boolean Algebra
- The three basic laws of Boolean Algebra are:
- Commutative law
- Associative law
- Distributive law
Commutative Law
- The logical operation carried between two Boolean variables when gives the same result irrespective of the order the two variables, then that operation is said to be Commutative. The logical OR & logical AND operations between x & y are shown below
x + y = y + x
x.y = y.x
- The symbol ‘+’ and ‘.’ indicates logical OR operation and logical AND operation.
- Commutative law holds good for logical OR & logical AND operations.
Associative Law
- If a logical OR operation of any two Boolean variables is performed first and then the same operation is performed with the remaining variable providing the same result, then that operation is said to be Associative. The logical OR & logical AND operations of x, y & z are:
x + (y + z) = (x + y) + z
x.(y.z) = (x.y).z
- Associative law holds good for logical OR & logical AND operations.
Distributive Law
- If a logical OR operation of any two Boolean variables is performed first and then AND operation is performed with the remaining variable, then that logical operation is said to be Distributive. The distribution of logical OR & logical AND operations between variables x, y & z are :
x.(y + z) = x.y + x.z
x + (y.z) = (x + y).(x + z)
- Distributive law holds good for logical OR and logical AND operations.
- These are the Basic laws of Boolean algebra and we can verify them by substituting the Boolean variables with ‘0’ or ‘1’.
Key Takeaways:
- The basic digital electronic circuit which has one or more inputs and single output is known as Logic gate.
- These Logic gates are known as the building blocks of any digital system. They can classified as:
Basic gates (AND, OR, NOT)
Universal gates (NAND, NOR)
Special gates( XOR, XNOR)
- The three basic laws of Boolean Algebra are:
- Commutative law
- Associative law
- Distributive law
- Four product combinations is obtained by combining two variables x and y with logical AND operation. They are called as min terms or standard product terms. The min terms are given as x’y’, x’y, xy’ and xy.
- In the same way, four Boolean sum terms is obtained by combining two variables x and y with logical OR operation. They are called as Max terms or standard sum terms. The Max terms are given as x + y, x + y’, x’ + y and x’ + y’.
The following table represents the min terms and MAX terms for 2 variables.
x | y | Min terms | Max terms |
0 | 0 | m0=x’y’ | M0=x + y |
0 | 1 | m1=x’y | M1=x + y’ |
1 | 0 | m2=xy’ | M2=x’ + y |
1 | 1 | m3=xy | M3=x’ + y’ |
- If the binary variable is ‘0’, then it is represented as complement of variable in min term and as the variable itself in Max term.
- Similarly, if it is ‘1’, then it is represented as complement of variable in Max term and as the variable itself in min term.
- From the above table, we can easily notice that min terms and Max terms are complement of each other.
- If there are ‘n’ Boolean variables, then there will be 2n min terms and 2n Max terms.
Canonical SoP and PoS forms
- A truth table comprises of a set of inputs and output(s).
- If there are ‘n’ input variables, then there shall be 2n possible combinations comprising of zeros and ones.
- So the value of every output variable depends on the combination of input variables.
- Hence, each output variable have ‘1’ for some combination and ‘0’ for other combination of input variables.
Therefore, we can express each output variable in two ways.
- Canonical SoP form
- Canonical PoS form
Example
Considering the following truth table.
Inputs | Output | ||
P | q | r | f |
0 | 0 | 0 | 0 |
0 | 0 | 1 | 0 |
0 | 1 | 0 | 0 |
0 | 1 | 1 | 1 |
1 | 0 | 0 | 0 |
1 | 0 | 1 | 1 |
1 | 1 | 0 | 1 |
1 | 1 | 1 | 1 |
- Here, the output (f) is ‘1’ for only four combinations of inputs.
- The corresponding min terms are given as p’qr, pq’r, pqr’, pqr.
- By doing logical OR, we get the Boolean function of output (f).
- Hence, the Boolean function of output is,
f = p’qr + pq’r + pqr’ + pqr.
- This is the desired canonical SoP form of output, f.
- It can also be represented as:
f=m3+m5+m6+m7f=m3+m5+m6+m7
f=∑m(3,5,6,7)f=∑m(3,5,6,7)
- First, we represented the function as sum of respective min terms and then, the symbol for summation of those min terms is used.
Standard SoP and PoS forms
Standard SoP form
- It stands for Standard Sum of Products form.
- In this, each product term need not contain all literals.
- So, the product terms can or cannot be the min terms.
- Therefore, it is therefore the simplified form of canonical SoP form.
Standard SoP of output variable can be obtained by two steps.
- Getting the canonical SoP form of output variable
- Simplification the above Boolean function.
The same procedure is followed for other output variables too, if there is more than one output variable.
Numerical
Convert the Boolean function into Standard SoP form.
f = p’qr + pq’r + pqr’ + pqr
Solution:
Step 1 – By using the Boolean postulate, x + x = x and also writing the last term pqr two more times we get
⇒ f = p’qr + pq’r + pqr’ + pqr + pqr + pqr
Step 2 – By Using Distributive law for 1st and 4th terms, 2nd and 5th terms, 3rdand 6th terms.
⇒ f = qr(p’ + p) + pr(q’ + q) + pq(r’ + r)
Step 3 – Then Using Boolean postulate, x + x’ = 1 we get
⇒ f = qr(1) + pr(1) + pq(1)
Step 4 – hence using Boolean postulate, x.1 = x we get
⇒ f = qr + pr + pq
⇒ f = pq + qr + pr
This is the required Boolean function.
Standard PoS form
- It stands for Standard Product of Sum form.
- Here, each sum term need not contain all literals.
- So, the sum terms can or cannot be the Max terms.
- Therefore, it is the desired simplified form of canonical PoS form.
Standard PoS form of output variable is obtained by two steps.
- Getting the canonical PoS form of output variable
- Simplification of the above Boolean function.
The same procedure is followed for other output variables too.
Numerical
Convert the Boolean function into Standard PoS form.
f = (p + q + r).(p + q + r’).(p + q’ + r).(p’ + q + r)
Solution:
Step 1 – By using the Boolean postulate, x.x = x and writing the first term p+q+r two more times we get
⇒ f = (p + q + r).(p + q + r).(p + q + r).(p + q + r’).(p +q’ + r).(p’ + q + r)
Step 2 – Now by using Distributive law, x + (y.z) = (x + y).(x + z) for 1st and 4thparenthesis, 2nd and 5th parenthesis, 3rd and 6th parenthesis.
⇒ f = (p + q + rr’).(p + r + qq’).(q + r + pp’)
Step 3 − Applying Boolean postulate, x.x’=0 for simplifying of the terms present in each parenthesis.
⇒ f = (p + q + 0).(p + r + 0).(q + r + 0)
Step 4 − Using Boolean postulate, x + 0 = x we get
⇒ f = (p + q).(p + r).(q + r)
⇒ f = (p + q).(q + r).(p + r)
This is the simplified Boolean function.
Hence, both Standard SoP and Standard PoS forms are Dual to one another.
Key Takeaways:
- Four product combinations is obtained by combining two variables x and y with logical AND operation. They are called as min terms or standard product terms. The min terms are given as x’y’, x’y, xy’ and xy.
- In the same way, four Boolean sum terms is obtained by combining two variables x and y with logical OR operation. They are called as Max terms or standard sum terms. The Max terms are given as x + y, x + y’, x’ + y and x’ + y’.
Canonical SoP form
- It means Canonical Sum of Products form.
- In this, each product term contains all literals.
- So that these product terms are nothing but the min terms.
- Hence is also known as sum of min terms form.
- Firstly, identification of the min terms is done and then the logical OR of those min terms is taken in order to get the Boolean expression (function) corresponding to that output variable.
- This Boolean function will be in sum of min terms form.
- Then following the same procedure for other output variables too.
Canonical PoS form
- It means Canonical Product of Sums form.
- Here In this form, each sum term contains all literals.
- These sum terms are the Max terms.
- Hence, canonical PoS form is also known as product of Max terms form.
- Identification of the Max terms for which the output variable is zero is done and then the logical AND of those Max terms is done in order to get the Boolean expression corresponding to that output variable.
- This Boolean function is in the form of product of Max terms.
- Following the same procedure for other output variables too.
Any arbitrary logic function can be expressed in the following forms:
- Sum-of-Products form (SOP)
Eg: Y(A,B,C,D)= AB+BC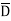 +CD ---------- Eq.(1)
+CD ---------- Eq.(1)
- Product-of-Sums form (POS)
Eg: Y(A,B,C,D)= (A+B+D) (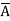 +
+ 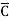 ) ---------- Eq.(2)
) ---------- Eq.(2)
Notice that in Eq.(1) and Eq.(2) , all the individual terms do not involve all the four literals.
If each term in SOP and POS forms contains all the literals then these are known as Standard (or Canonical) SOP and POS.
Thus, a Standard SOP form is one in which a number of product terms, each one of which contains all the variables of the function either in complemented or non-complemented form, are summed together. Each individual product term in standard SOP form is called a minterm.
Eg: Y = ABCD+ABC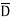 +
+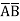 CD
CD
A Standard POS form is the one in which a number of sum terms, each one of which contains all the variables of the function either in complemented or in non-complemented form, are multiplied together. Each individual sum term in standard POS form is called a maxterm.
Eg: Y= (A+B+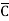 +D) (
+D) (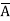 +B+
+B+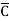 +D)
+D)
Any given SOP/POS function which is not in its standard form, can always be converted to a standard from by unreducing, that is, “expanding’ the function.
EXPANSION OF A BOOLEAN FUNCTION TO STANDARD SOP FORM
Any SOP equation can be converted to standard SOP by ANDing the terms in the expression with terms formed by ORing the variable and its complement which are not present in that term.
Eg: ConvertY = A + B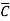 +AB
+AB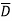 +ABCD to standard SOP form.
+ABCD to standard SOP form.
Solution: Y = A + B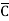 +AB
+AB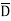 +ABCD
+ABCD
= A(B+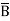 )(C+
)(C+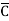 )(D+
)(D+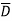 ) + B
) + B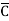 (A+
(A+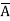 )( D+
)( D+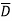 ) + AB
) + AB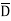 (C+
(C+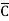 )
)
= ABCD+ ABC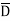 +AB
+AB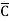 D +AB
D +AB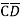 +A
+A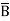 CD+ A
CD+ A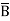 C
C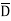 +A
+A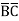 D +A
D +A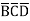 +
+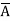 B
B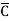 D+
D+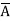 B
B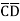
= m15 + m14 + m13+ m12 + m11+ m10 + m9+ m8 + m5 + m4
=∑m(15,14,13,12,11,10,9,8,5,4)
NOTE: Each minterm is represented by mi where the subscript i is the decimal equivalent of the natural binary number corresponding to the minterm with uncomplemented variables taken as 1’s and the complemented variables taken as 0’s.
EXPANSION OF A BOOLEAN FUNCTION TO STANDARD POS FORM
Any POS equation can be converted to standard POS by ORing the terms in the expression with terms formed by ANDing the variable and its complement which are not present in that term.
Eg: Convert Y = (A+B)(A+C)(B+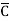 ) to a standard POS form.
) to a standard POS form.
Solution: Y = (A+B)(A+C)(B+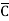 )
)
= (A+B+C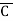 )(A+B
)(A+B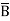 +C) (A
+C) (A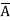 +B+
+B+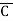 )
)
= (A+B+C)(A+B+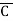 )(A+B+C)(A+
)(A+B+C)(A+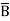 +C) (A+B+
+C) (A+B+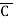 )(
)(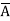 +B+
+B+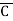 )
)
= (A+B+C) (A+B+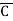 )(A+
)(A+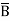 +C) (
+C) (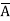 +B+
+B+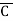 )
)
= M0 + M1 + M2 + M5
= πM (0,1,2,3)
NOTE: Each maxterm is represented by Mi where the subscript i is the decimal equivalent of the natural binary number corresponding to the maxterm with uncomplemented variables taken as 0’s and the complemented variables taken as 1’s.
In general, for a n-variable logical function there are 2n minterms and 2n maxterms. The possible minterms/maxterms for a 4-variable function is shown below:
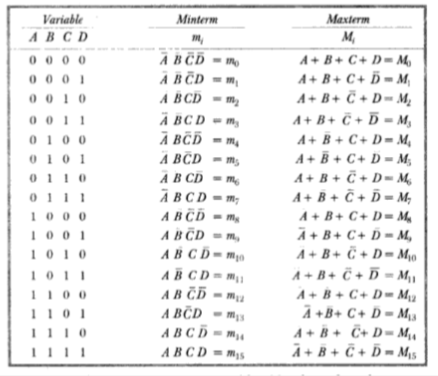
If a logical function is specified interms of minterms/maxterms its minterm/maxterm representation can be determined using complementary property. For example, for a 4-variable function if:
Y = ∑m (0,3,6,7,10,12,15)
Then Y = πM (1,2,4,5,8,9,11,13,14)
Theorems of Boolean Algebra
- The following theorems are used in Boolean algebra.
- Duality theorem
- De Morgan’s theorem
Duality Theorem
- It states that “The dual of the Boolean function is obtained by interchanging the logical AND operator with logical OR operator and zeros with ones”.
- For every Boolean function, there is a Dual function.
- Let us make the Boolean equations (relations) of Boolean postulates and basic laws into two groups. The following table shows these two groups.
Group1 | Group2 |
x + 0 = x | x.1 = x |
x + 1 = 1 | x.0 = 0 |
x + x = x | x.x = x |
x + x’ = 1 | x.x’ = 0 |
x + y = y + x | x.y = y.x |
x + (y + z) = (x + y) + z | x.(y.z) = (x.y).z |
x.(y + z) = x.y + x.z | x + (y.z) = (x + y).(x + z) |
- Every row comprise of two Boolean equations and they are dual to one other.
- We can also verify the Boolean equations of Group1 and 2 by using duality theorem.
De Morgan’s Theorem
- It is useful in finding the complement of Boolean function.
- It states that “The complement of logical OR of at least two Boolean variables is equal to the logical AND of each complemented variable”.
- It can be represented using 2 Boolean variables x and y as
(x + y)’ = x’.y’
- The dual of the above Boolean function is
(x.y)’ = x’ + y’
- Therefore, the complement of logical AND of the two Boolean variables is equivalent to the logical OR of each complemented variable.
- Similarly, DeMorgan’s theorem can be applied for more than 2 Boolean variables also.
Numerical
- Simplify the Boolean function,
f = p’qr + pq’r + pqr’ + pqr
Method 1
Given
f = p’qr + pq’r + pqr’ +pqr.
In first and second term r is common and in third and fourth terms pq is common.
So, taking out the common terms by using Distributive law we get,
⇒ f = (p’q + pq’)r + pq(r’ + r)
The terms present in first parenthesis can be simplified by using Ex-OR operation.
The terms present in second parenthesis is equal to ‘1’ using Boolean postulate we get
⇒ f = (p ⊕q)r + pq(1)
The first term can’t be simplified further.
But, the second term is equal to pq using Boolean postulate.
⇒ f = (p ⊕q)r + pq
Therefore, the simplified Boolean function is f = (p⊕q)r + pq
Method 2
Given f = p’qr + pq’r + pqr’ + pqr.
Using the Boolean postulate, x + x = x.
Hence we can write the last term pqr two more times.
⇒ f = p’qr + pq’r + pqr’ + pqr + pqr + pqr
Now using the Distributive law for 1st and 4th terms, 2nd and 5th terms, 3rdand 6th terms we get.
⇒ f = qr(p’ + p) + pr(q’ + q) + pq(r’ + r)
Using Boolean postulate, x + x’ = 1 and x.1 = x for further simplification .
⇒ f = qr(1) + pr(1) + pq(1)
⇒ f = qr + pr + pq
⇒ f = pq + qr + pr
Therefore, the simplified Boolean function is f = pq + qr + pr.
Hence we got two different Boolean functions after simplification of the given Boolean function. Functionally, these two functions are same. As per requirement, we can choose one of them.
Numerical
Find the complement of the Boolean function,
f = p’q + pq’.
Solution:
Using DeMorgan’s theorem, (x + y)’ = x’.y’ we get
⇒ f’ = (p’q)’.(pq’)’
Then by second law, (x.y)’ = x’ + y’ we get
⇒ f’ = {(p’)’ + q’}.{p’ + (q’)’}
Then by using, (x’)’=x we get
⇒ f’ = {p + q’}.{p’ + q}
⇒ f’ = pp’ + pq + p’q’ + qq’
Using x.x’=0 we get
⇒ f = 0 + pq + p’q’ + 0
⇒ f = pq + p’q’
Therefore, the complement of Boolean function, p’q + pq’ is pq + p’q’.
Key Takeaways:
- Two theorems are used in boolean algebra duality theorem and de-morgan’s theorem.
- Duality theorem states that “The dual of the Boolean function is obtained by interchanging the logical AND operator with logical OR operator and zeros with ones”.
- De-morgan’s theorem states that “The complement of logical OR of at least two Boolean variables is equal to the logical AND of each complemented variable”.
Karnaugh’s map, don’t care conditions
- Karnaugh introduced a method for simplification of Boolean functions in an very easy way.
- This method is known as Karnaugh map method or K-map method.
- It is a graphical method, which comprises of 2n cells for ‘n’ variables.
- Here, the adjacent cells varies only in single bit position.
K-Maps for 2 to 5 Variables
It is the most suitable method for minimizing Boolean functions of 2 variables to 5 variables.
2 Variable K-Map
It has 4 number of cells since the number of variables is two.
The 2 variable K-Map is :
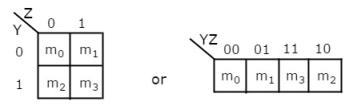
Fig.6 : 2 variable K-Map (ref. 1)
- The only way to group 4 adjacent min terms.
- The possible combinations are {(m0, m1), (m2, m3), (m0, m2) and (m1, m3)}.
3 Variable K-Map
It has 8 number of cells since the number of variables is 3.
The 3 variable K-Map is:
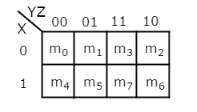
Fig.7 : 3 variable K-Map
- The only way to group 8 adjacent min terms.
- The possible are {(m0, m1, m3, m2), (m4, m5, m7, m6), (m0, m1, m4, m5), (m1, m3, m5, m7), (m3, m2, m7, m6) and (m2, m0, m6, m4)}.
- The possible combinations of grouping 2 adjacent min terms are {(m0, m1), (m1, m3), (m3, m2), (m2, m0), (m4, m5), (m5, m7), (m7, m6), (m6, m4), (m0, m4), (m1, m5), (m3, m7) and (m2, m6)}.
- If x=0, then 3 variable K-map becomes 2 variable K-map.
4 Variable K-Map
It has 16 number of cells since the number of variables is 4.
The 4 variable K-Map is:
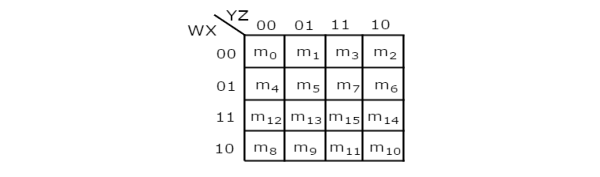
Fig.8 : 4 variable K-Map
- The only way to group 8 adjacent min terms.
- Let R1, R2, R3 and R4 represents the min terms of first row, second row, third row and fourth row respectively.
- Similarly, C1, C2, C3 and C4 represents the min terms of first column, second column, third column and fourth column respectively.
- The possible combinations are {(R1, R2), (R2, R3), (R3, R4), (R4, R1), (C1, C2), (C2, C3), (C3, C4), (C4, C1)}.
- If w=0, then 4 variable K-map becomes 3 variable K-map.
Rules for simplifying K-maps:
- Selecting K-map on the basis of number of variables present in the Boolean function.
- If the Boolean function is in Max terms form, then place the zeroes at respective Max term cells in theK-map.
- If the Boolean function is in PoS form, then place the zeroes wherever required in K-map for which the given sum terms are valid.
- The maximum possibilities of grouping is checked for adjacent zeroes.
- It should be of powers of two.
- Starting from highest power of two and to the least power of two.
- Highest power is equivalent to the number of variables considered in K-map and least power is zero.
- Each group will give either a literal or one sum term.
- It is known as prime implicant.
- The prime implicant is an essential prime implicant when at least a single ‘0’ is not covered with any other groups but only that grouping covers.
- The simplified Boolean function contains all essential prime implicants and only the required prime implicants.
Numericals
Simplify f(X,Y,Z)=∏M(0,1,2,4)f(X,Y,Z)=∏M(0,1,2,4)using K-map.
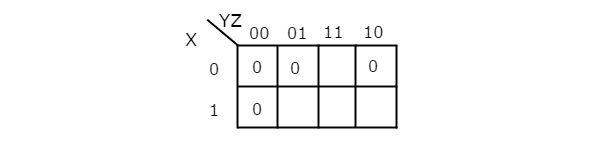
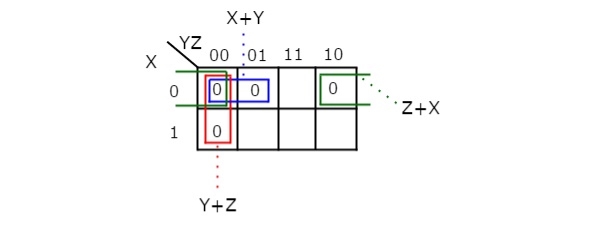
Therefore, the simplified Boolean function is
f = (X + Y).(Y + Z).(Z + X)
Simplify:
F(P,Q,R,S)=∑(0,2,5,7,8,10,13,15)
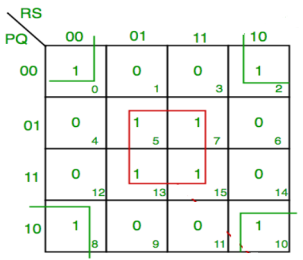
F = P’Q’R’S’ + PQ’R’S’ + P’Q’RS’ +PQ’RS’ + QS
F = P’Q’S’ + PQ’S’ + QS
F = Q’S’ +QS
Simplify:
F(A,B,C)=π(0,3,6,7)
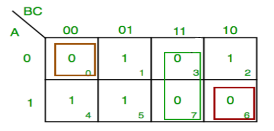
F = A’BC +ABC +A’B’C’ +ABC’
F = BC + C’ ( A’B’ + AB )
For more details please visit https://www.youtube.com/watch?v=wjM2RDG5yTI
Key Takeaways:
- K-map is a graphical method, which comprises of 2n cells for ‘n’ variables.
- It is a method for simplification of Boolean functions in an very easy way.
- It is used for 5 variables at the max.
Reference Books:-
1) “Digital Fundamentals”, Floyd and Jain, Pearson
2) “Digital Logic and Computer design”, M. Morris Mano, Pearson
3) “Fundamentals of Digitals Circuits”, A. Anand Kumar, PHI
4) “Digital Systems”, Ronald J. Tocci, Neal S. Widmer, Pearson