UNIT 1
Atomic Structure And Bonding In Materials
Every atom consists of a small nucleus composed of protons and neutrons, which is encircled by moving electrons in their orbital, specific energy levels.
The top most orbital electrons, valence electrons, affect most material properties that are of interest to engineer. E.g.: chemical properties, nature of bonding, size of atom, optical/magnetic/electrical properties.
Electrons and protons are negative and positive charges of the same magnitude being 1.60x10-19 coulombs.
Neutrons are electrically neutral.
Protons and neutrons have approximately the mass, 1.67x10-27 kg, which is larger than that of an electron, 9.11x10-31 kg.
Atomic number (Z) - is the number of protons per atoms.
Atomic mass (A) - is the sum of the masses of protons and neutrons within the nucleus.
Atomic mass is measured in atomic mass unit (amu) where
1amu=(1\12) the mass of most common isotope of carbon atom, measured in grams.
A = Z+N, where N is number of neutrons.
Isotopes - atoms with same atomic number but different atomic masses.
A mole is the amount of matter that has a mass in grams equal to the atomic mass in amu of the atoms. Thus a mole of carbon has a mass of 12 grams.
Bonds are two kinds – Primary, and Secondary
Primary bonds – relatively stronger. Exists in almost all solid materials. E.g.: Ionic, Covalent, and Metallic bonds.
Secondary bonds – relatively weaker bonds. Exists in many substances like water along with primary bonds. E.g.: Hydrogen and Vander Waals forces.
- All solid materials are made of atoms/molecules, which are arranged in specific order in some materials, called crystalline solids. Otherwise non-crystalline or amorphous solids.
- Groups of atoms/molecules specifically arranged – crystal.
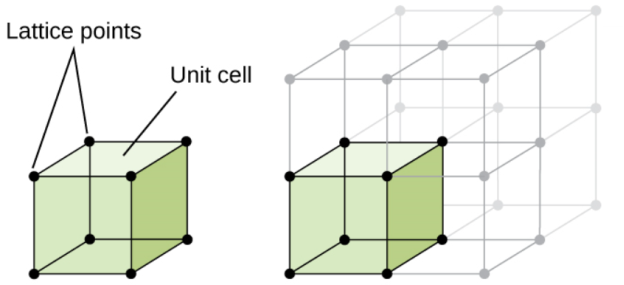
- Lattice is used to represent a three-dimensional periodic array of points coinciding with atom positions.
- Unit cell is smallest repeatable entity that can be used to completely represent a crystal structure. It is the building block of crystal structure.
It is characterized by:
Type of atom and their radii, R
Cell dimensions, a and c (for hexagonal structures)
Number of atoms per unit cell, n
Coordination number (CN)– closest neighbours to an atom
Atomic packing factor, APF
Most common unit cells – Face-centred cubic, Body centred cubic and Hexagonal.
Single-crystal X-ray Diffraction is a non-destructive analytical technique which provides detailed information about the internal lattice of crystalline substances, including unit cell dimensions, bond-lengths, bond-angles, and details of site-ordering. Directly related is single-crystal refinement, where the data generated from the X-ray analysis is interpreted and refined to obtain the crystal structure.
Principle
X-ray diffraction is based on constructive interference of monochromatic X-rays and a crystalline sample. These X-rays are generated by a cathode ray tube, filtered to produce monochromatic radiation, collimated to concentrate, and directed toward the sample. The interaction of the incident rays with the sample produces constructive interference (and a diffracted ray) when conditions satisfy Bragg's Law (nλ=2d sinθ).
This law relates the wavelength of electromagnetic radiation to the diffraction angle and the lattice spacing in a crystalline sample. These diffracted X-rays are then detected, processed and counted. By changing the geometry of the incident rays, the orientation of the centered crystal and the detector, all possible diffraction directions of the lattice should be attained.
All diffraction methods are based on generation of X-rays in an X-ray tube. These X-rays are directed at the sample, and the diffracted rays are collected. A key component of all diffraction is the angle between the incident and diffracted rays. Powder and single-crystal diffraction vary in instrumentation beyond this.
Working:
X-ray diffractometer consist of three basic elements, an X-ray tube, a sample holder, and an X-ray detector. X-rays are generated in a cathode ray tube by heating a filament to produce electrons, accelerating the electrons toward a target by applying a voltage, and impact of the electrons with the target material. When electrons have sufficient energy to dislodge inner shell electrons of the target material, characteristic X-ray spectra are produced.
These spectra consist of several components, the most common being Kα and Kβ. Kα consists, in part, of Kα1 and Kα2. Kα1 has a slightly shorter wavelength and twice the intensity as Kα2. The specific wavelengths are characteristic of the target material. Filtering, by foils or crystal monochromators, is required to produce monochromatic X-rays needed for diffraction. Kα1and Kα2 is sufficiently close in wavelength such that a weighted average of the two is used.
Molybdenum is the most common target material for single-crystal diffraction, with MoKα radiation = 0.7107Å. These X-rays are collimated and directed onto the sample. When the geometry of the incident X-rays impinging the sample satisfies the Bragg Equation, constructive interference occurs.
A detector records and processes this X-ray signal and converts the signal to a count rate which is then output to a device such as a printer or computer monitor. X-rays may also be produced using a synchotron, which emits a much stronger beam.
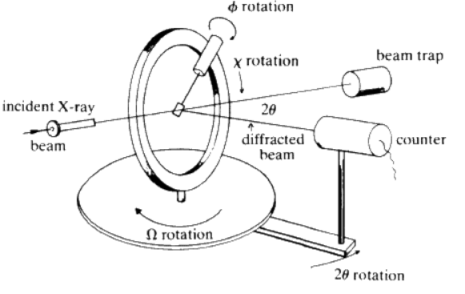
Fig: Circle Diffractometer
- A system of notation is required to identify particular direction(s) or plane(s) to characterize the arrangement of atoms in a unit cell.
- Formulas involving Miller indices are very similar to related formulas from analytical geometry – simple to use.
- Use of reciprocals avoids the complication of infinite intercepts.
- Specifying dimensions in unit cell terms means that the same label can be applied to any plane with a similar stacking pattern, regardless of the crystal class of the crystal. Plane (111) always steps the same way regardless of crystal system
Direction:
- A vector of convenient length is placed parallel to the required direction.
- The length of the vector projection on each of three axes is measured in terms of unit cell dimensions.
- These three numbers are made to smallest integer values, known as indices, by multiplying or dividing by a common factor.
- The three indices are enclosed in square brackets, [uvw].
- A family of directions is represented by <uvw>
Plane:
- Determine the intercepts of the plane along the crystallographic axes, in terms of unit cell dimensions.
- If plane is passing through origin, there is a need to construct a plane parallel to original plane.
- Take the reciprocals of these intercept numbers Clear fractions Reduce to set of smallest integers
- The three indices are enclosed in parenthesis, (hkl).
- A family of planes is represented by {hkl}
The three cubic unit cells: simple cubic, body-centred cubic unit cell, and face-centred cubic unit cell
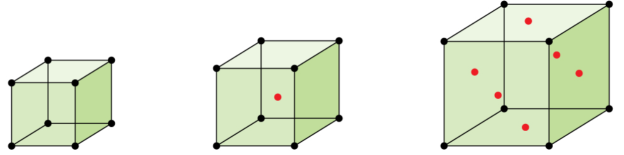
Fig: Lattice point location
Some metals crystallize in an arrangement that has a cubic unit cell with atoms at all of the corners and an atom in the centre, as shown in Figure. This is called a body-centred cubic (BCC) solid. Atoms in the corners of a BCC unit cell do not contact each other but contact the atom in the centre. A BCC unit cell contains two atoms: one-eighth of an atom at each of the eight corners (8×18=18×18=1 atom from the corners) plus one atom from the centre. Any atom in this structure touches four atoms in the layer above it and four atoms in the layer below it. Thus, an atom in a BCC structure has a coordination number of eight.
Many other metals, such as aluminium, copper, and lead, crystallize in an arrangement that has a cubic unit cell with atoms at all of the corners and at the centres of each face, as illustrated in Figure. This arrangement is called a face-centred cubic (FCC) solid. A FCC unit cell contains four atoms: one-eighth of an atom at each of the eight corners (8×18=18×18=1 atom from the corners) and one-half of an atom on each of the six faces (6×12=36×12=3 atoms from the faces). The atoms at the corners touch the atoms in the centres of the adjacent faces along the face diagonals of the cube. Because the atoms are on identical lattice points, they have identical environments.
Numerical:
Calculation of Atomic Radius and Density for Metals
Calcium crystallizes in a face-centered cubic structure. The edge length of its unit cell is 558.8 pm.
(a) What is the atomic radius of Ca in this structure?
(b) Calculate the density of Ca.
Solution:
(a) In an FCC structure, Ca atoms contact each other across the diagonal of the face, so the length of the diagonal is equal to four Ca atomic radii (d = 4r). Two adjacent edges and the diagonal of the face form a right triangle, with the length of each side equal to 558.8 pm and the length of the hypotenuse equal to four Ca atomic radii:
a2+a2=d2⟶(558.8pm)2+(558.5pm)2=(4r)2
Solving this gives
r=√[(558.8pm)2+(558.5pm)2]/16
=197.6pmg
(b) Density is given by density=mass/volume.
The density of calcium can be found by determining the density of its unit cell: for example, the mass contained within a unit cell divided by the volume of the unit cell. A face-centered Ca unit cell has one-eighth of an atom at each of the eight corners (8×1/8=1 atom) and one-half of an atom on each of the six faces(6×1/2=3), for a total of four atoms in the unit cell.
The mass of the unit cell can be found by: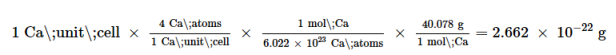
The volume of a Ca unit cell can be found by:
V=a3= (558.8×10−10cm)3=1.745×10−22cm3
(Note that the edge length was converted from pm to cm to get the usual volume units for density.)
Then, the density of Po=2.662×10−22g/1.745×10−22cm3=1.53g/ cm3
Ionic Solid
Ionic solids are solids held together by ionic bonds. They are lattices composed of oppositely charged ions. Ionic solids tend to have high melting points ("high" generally being higher than metallic but lower than covalent). Because the electrons in ionic solids are localized (in the ions) these solids tend to be stiff and brittle like covalent solids.
As solids they do not conduct electricity (again because of the localize electrons). However, they do conduct electricity as liquids (or when dissolved in water) since then the ions can move.
Examples of ionic solids include NaCl and Ca(CO3). Ionic compounds are all generally found in nature as ionic solids.
Covalent Solids
Covalent solids, also called network solids, are solids that are held together by covalent bonds. As such, they have localized electrons (shared between the atoms) and the atoms are arranged in fixed geometries. Distortion away from this geometry can only occur through a breaking of covalent sigma bonds. As a result, the melting point of covalent solids is extremely high. They also tend to be extremely hard substances that will break into pieces rather than smoothly change shape. We say that they are stiff and brittle.
Examples of covalent solids include diamond and silica (SiO2).
The definition of an amorphous solid is any substance that lacks long-range order or geometrical shape. A great way to remember this type of solid is to think of the prefix 'amorph-', which means lacking shape.
A solid is a material that has a defined shape. In chemistry, solids are referred to as states of matter that are not just defined by shape but also volume. There are two types of solids: crystalline and amorphous solids. Think of these as the odd couple. They are complete opposites. Crystalline solids have long-range order, meaning that their structure is much defined and carries a distinct pattern. This is quite different from our friend, the amorphous solid, who lacks rigidity and distinct patterning
Because these solids lack a defined shape, the strength of the bonds that hold the atoms together can vary. Some of those bonds (seen in diagram 1) can be weaker or stronger than others. This contributes to another property of amorphous solids: they do not have a well-defined melting point.
The melting point of this solid can change, depending on the heat applied to the substance. Substance A may melt very fast as the bonds are weak and susceptible to breaking, when heat is applied. On the other hand, substance B may take a longer time to melt as those bonds are much stronger and refuse to break when heat is applied.
Single Crystalline
Crystalline can be a crystal, composed of crystal, or resemble a crystal. Crystalline solids or crystals have ordered structures and symmetry. The atoms, molecules, or ions in crystals are arranged in a particular manner, thus have a long-range order. In crystalline solids, there is a regular, repeating pattern; thus, we can identify a repeating unit. By definition, “a crystal is a homogenous chemical compound with a regular and periodic arrangement of atoms. Examples are halite, salt (NaCl), and quartz (SiO2).
Polycrystalline
In nature, most of the time, crystals appear to have disrupted their long-range order. Polycrystalline are solids that are composed of many numbers of small crystals. These are arranged in different orientations and are bound by highly defective boundaries. The crystals in a polycrystalline solid are microscopic, and they are known as crystallites. These are also known as grains. There are solids, which are composed of a single crystal like gems, silicon single crystals. However, these occur very rarely in nature. Most of the time solids are polycrystalline. In a structure like this, number of single crystals is held together by a layer of amorphous solids. Amorphous solid is a solid, which lacks a crystalline structure. That is, it does not have long range ordered arrangement of atoms, molecules or ions within the structure. Therefore, in a polycrystalline structure, the long-range order has been disrupted. For example, all the metals and ceramics are polycrystalline.
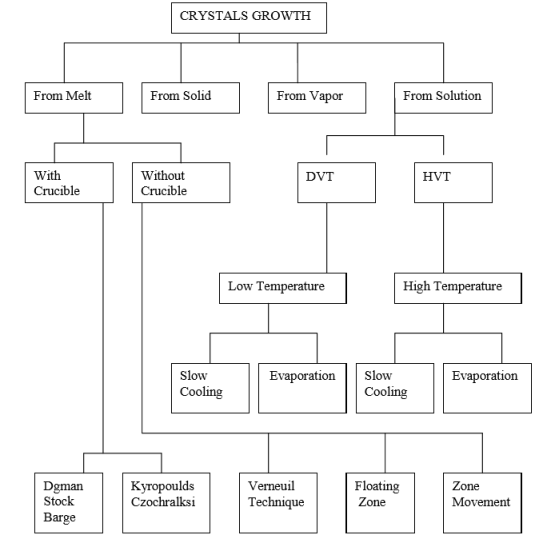
Crystal growth is a challenging task and the technique followed for crystal growth depends upon the characteristics of the materials under investigation, such as its melting point, Volatile nature, solubility in water or other organic solvents and so on.
- Growth from melt.
- Growth from vapour.
- Growth from solution.
- Growth from solid.
Reference
i) Electrical Engineering Materials, Dr. G.P. CHHALOTRA & Dr. B.K.BHAT, Khanna Technical Publications.
