Unit – 1
Polynomials
Legendre’s Equation
Another differential equation of importance in Applied Mathematics, particularly in boundary value problems for spheres, is Legendre’s equation
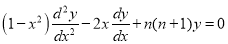… (1)
Here n is a real number. But in most applications only integral values of n are required. Substituting
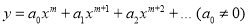
(1) Takes the for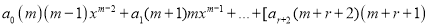 
Equating to zero the coefficient of the lowest power of x, i.e., of
, we get
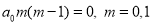
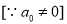
Equating to zero the coefficient of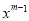 
and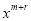
, we get 
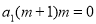…. (2)
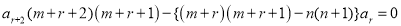…. (3)
When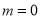
, (2) is satisfied and therefore, 
. Then (3) gives, taking 
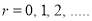in turn,
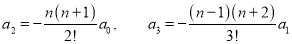
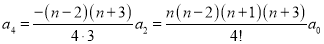
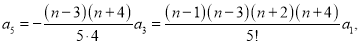Etc.
Hence for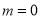
, there are two independent solutions of (1):
…. (4)
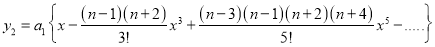…. (5)
When m=1, (2) shows that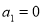
. Therefore, (3) gives
And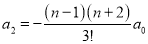 
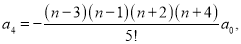Etc.
Thus for
, we get the solution (5) again. Hence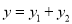
is the general solution of (1).
If n is a positive even integer, the series (4) terminates at the term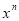 
and 
becomes a polynomial. Similarly if n is an odd integer, (5) becomes a polynomial of degree n. Thus, whenever n is a positive integer, the general solution of (1) consists of polynomial solution and an infinite series solution.
These polynomial solutions, with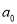 
or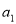 
so chosen that the value of the polynomial is 1 for
, are called Legendre polynomials of order n and are denoted by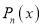
. The infinite series solution with (
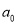or 
properly chosen) is called Legendre function of the second kind and is denoted by
.
Rodrigue’s Formula
We shall prove that 
…. (1)
Let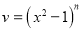 
. Then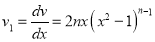 
i.e.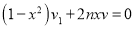 
…. (2)
Differentiating (2), (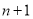
) times by Leibnitz’s theorem
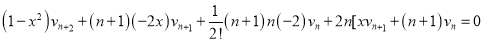
Or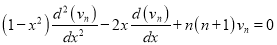 
Which is Legendre’s equation and 
is its solution. Also its finite series solution is
.
…. (3)
To determine the constant c, put x=1 in (3). Then
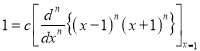
Terms containing
and its powers
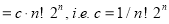
Substituting this value of c in (3), we get (1), which is known as the Rodrigue’s formula.
Obs: All roots of  |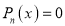
(2) Legendre polynomials. Using (1), we get
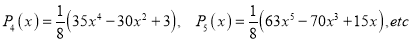
In general, we have
…. (4)
Where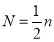 
or 
according as n is even or odd.
Let us derive (4) from (1).
By Binomial theorem, 
This is same as (4), and the last term
is such that the power of 
for this term is either 0 or 1.
Example. Express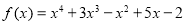 
in terms of Legendre polynomials.
Solution:
Since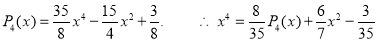 
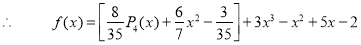
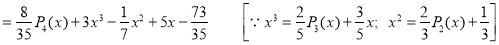
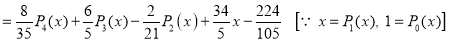
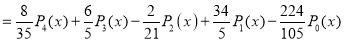
Example:
Show that for any function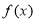
, which the nth derivative is continuous,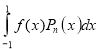 
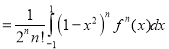
Solution: Using Rodrigue’s Formula: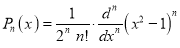
[Integrate by parts]
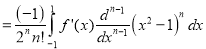
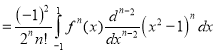[Again integrating by parts]
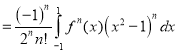[Integrating by parts (n - 2) times]
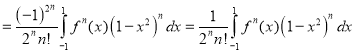
Orthogonality of Legendre Polynomials
We shall prove that,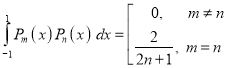 
We know that the solutions of
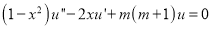…. (1)
…. (2)
Are 
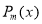and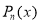
respectively.
Multiplying (1) by v and (2) by u and subtracting, we get
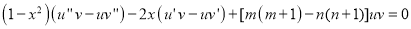
Or 
Now integrating from -1 to 1 we get
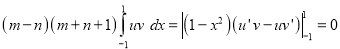
Hence 
This is known as the orthogonality property of Legendre polynomials.
When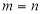
, we have from Rodrigue’s formula,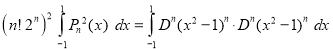
Since 
has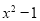 
as a factor, the first term on the right vanishes for
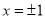. Thus
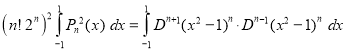
[Integrate by parts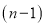 
times]
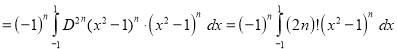
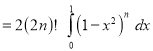[Put
]
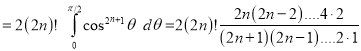
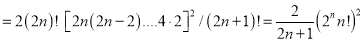
Hence,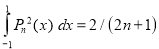 
Example.
Prove that
Solution:
We know that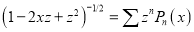 
Squaring both sides we get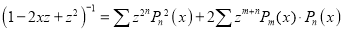 
Integrating both sides between -1 and 1 we have
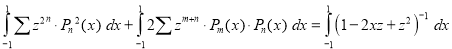
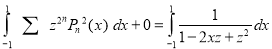
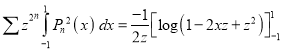
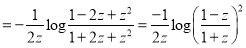
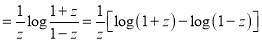
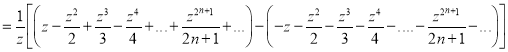
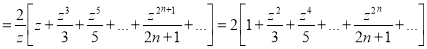
Equating the coefficient of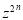 
on both sides, we have
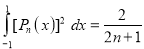
Hence
Example:
Assuming that a polynomial 
of degree n can be written as
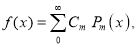
Show that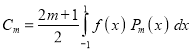 
Solution:
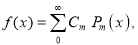
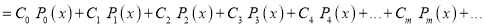
Multiplying both sides by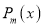
we get
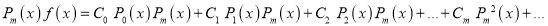
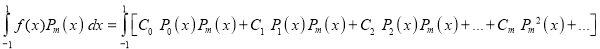
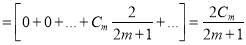
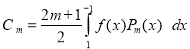
CHEBYSEV POLYNOMIALS (Techebcheff or Tschebyscheff polynomials)
The Chebysev polynomials of first kind
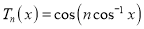
And the second kind
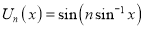
Where n is non – negative integer.
Chebyshev equation
…. (1)
Prove that 
and
are the independent solution of the Chebyshev equation
Proof:
Let 
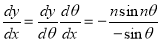
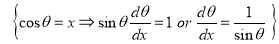
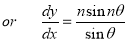
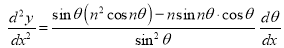
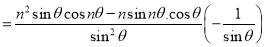
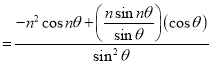
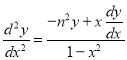
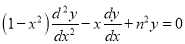
Which is satisfied by
.
Similarly we can prove that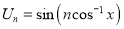 
is a solution of Chebyshev equation.
Hence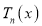 
and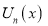 
both are the solutions of (1). But
cannot be expressed as a constant multiple of 
as shown below:
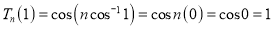
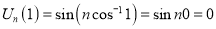
Thus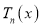 
and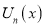 
are independent solutions of Cheybshev’s Equation.
Orthogonal Properties of Chebyshev Polynomials
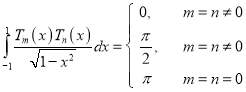
Proof: We know that
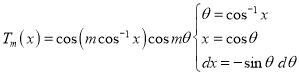
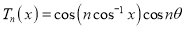
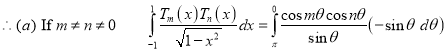
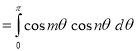
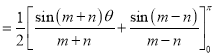
(b) If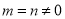 
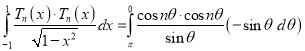
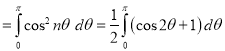
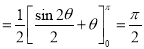
(c) If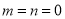 
Note: (1) Similarly we can prove that
(2) The polynomials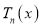 
are orthogonal with the function
.
Example 1: Prove that (a) 
(b)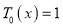 
(c)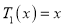
Solution: The Chebyshev polynomial of degree n over the integral [-1, 1] is define as
…. (1)
(a) On putting –n for n in (1) we get
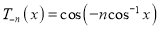
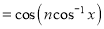
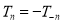
(b) Let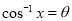 
so that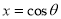 
On Putting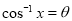 
in (1), it becomes
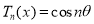…. (2)
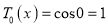
(c) If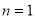 
on putting 
in (1) we get 
Example 2:
Prove that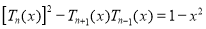 
Solution:
Let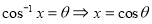 
Hence proved.
Example 3:
Prove that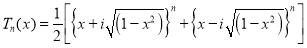 
Solution:
We know that 
…. (1)
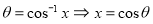
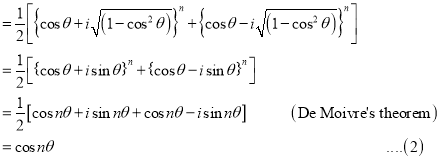
From (1) and (2) we have
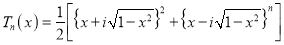
Hence Proved.
In the mathematical subfields of numerical analysis and mathematical analysis, a trigonometric polynomial is a finite linear combination of functions sin (nx) and cos (nx) with n taking on the values of one or more natural numbers. The coefficients may be taken as real numbers, for real-valued functions. For complex coefficients, there is no difference between such a function and a finite Fourier series.
Trigonometric polynomials are widely used, for example in trigonometric interpolation applied to the interpolation of periodic functions. They are used also in the discrete Fourier transform.
The term trigonometric polynomial for the real-valued case can be seen as using the analogy: the functions sin (nx) and cos (nx) are similar to the monomial basis for polynomials. In the complex case the trigonometric polynomials are spanned by the positive and negative powers of eix
By a trigonometric polynomial we mean a function of the form
(1)
Where 
and 
are constants which allowed to be complex. One can think of such function as a combination of several harmonics (described by sinusoidal functions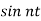 
and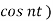 
for a musical instrument;
An alternative description of this function is
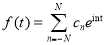(2)
Indeed, using 
and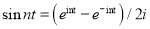
, we can convert (1) into the form (2) Using
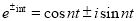we can turn (1) back to (1).
We prefer to use (2) because
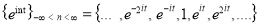
Is an orthonormal system with respect to the inner product
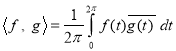
As we know, the general theory of orthonormal systems tells us that the coefficient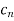 
(7.2) is given by the following recipe:
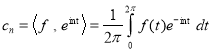(3)
In the present chapter, we use the method of harmonic analysis to derive Cauchy’s formula for polynomials and Poisson formula for trigonometric polynomials, which will be extended in the future for more general functions. Both formulas are extremely important: they are keys to our future chapters, one for complex analysis and the other for harmonic analysis. The basic tactic in our approach is to exploit the orthonormality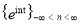
. Before we start, we show two (related) examples in order help the reader to appreciate this tactic.
Example 1: We wish to find the integral
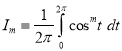
For any positive integer m. When m is odd, clearly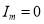
. So we may assume m to be even, say 
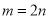. Now.
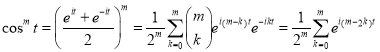
Notice that, from the above discussion, we have
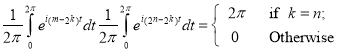
So, writing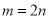
, we have
Example 2:
We have established that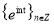 
is an ONS (orthonormal system). The identity
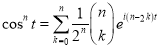
Can be viewed as an orthogonal decomposition with respect to this ONS (Here we replace m by n. This identity holds without assuming m even.) So we may apply Pythagoras identity to obtain
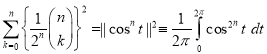
Which is
, according to the last example, so we obtain
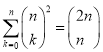
Take a polynomial function
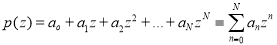
In a complex variable z. For convenience, we ignore N and rewrite it as
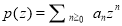(7.4)
With the understanding that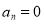 
for
. Let us restrict it to the unit circle by considering the function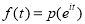
. Then
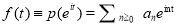(7.5)
This is a trigonometric polynomial and its coefficient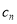 
are given by
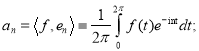
Wavelet Transform:
The wavelet transform is similar to the Fourier transform (or much more to the windowed Fourier transform) with a completely different merit function. The main difference is this: Fourier transform decomposes the signal into sines and cosines, i.e. the functions localized in Fourier space; in contrary the wavelet transform uses functions that are localized in both the real and Fourier space. Generally, the wavelet transform can be expressed by the following equation:
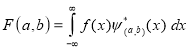
Where the * is the complex conjugate symbol and function ψ is some function. This function can be chosen arbitrarily provided that it obeys certain rules.
As it is seen, the Wavelet transform is in fact an infinite set of various transforms, depending on the merit function used for its computation. This is the main reason, why we can hear the term “wavelet transform” in very different situations and applications. There are also many ways how to sort the types of the wavelet transforms. Here we show only the division based on the wavelet orthogonality. We can use orthogonal wavelets for discrete wavelet transform development and non-orthogonal wavelets for continuous wavelet transform development. These two transforms have the following properties:
- The discrete wavelet transform returns a data vector of the same length as the input is. Usually, even in this vector many data are almost zero. This corresponds to the fact that it decomposes into a set of wavelets (functions) that are orthogonal to its translations and scaling. Therefore we decompose such a signal to a same or lower number of the wavelet coefficient spectrum as is the number of signal data points. Such a wavelet spectrum is very good for signal processing and compression, for example, as we get no redundant information here.
2. The continuous wavelet transform in cotrary returns an array one dimension larger than the input data. For a 1D data we obtain an image of the time-frequency plane. We can easily see the signal frequencies evolution during the duration of the signal and compare the spectrum with other signals spectra. As here is used the non-orthogonal set of wavelets, data are highly correlated, so big redundancy is seen here. This helps to see the results in a more humane form.
Discrete Wavelet Transform 
The discrete wavelet transform (DWT) is an implementation of the wavelet transform using a discrete set of the wavelet scales and translations obeying some defined rules. In other words, this transform decomposes the signal into mutually orthogonal set of wavelets, which is the main difference from the continuous wavelet transform (CWT), or its implementation for the discrete time series sometimes called discrete-time continuous wavelet transform (DT-CWT).
The wavelet can be constructed from a scaling function which describes its scaling properties. The restriction that the scaling functions must be orthogonal to its discrete translations implies some mathematical conditions on them which are mentioned everywhere, e.g. The dilation equation
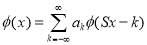
Where S is a scaling factor (usually chosen as 2). Moreover, the area between the function must be normalized and scaling function must be orthogonal to its integer translations, i.e.
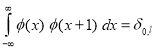
After introducing some more conditions (as the restrictions above does not produce a unique solution) we can obtain results of all these equations, i.e. the finite set of coefficients ak that define the scaling function and also the wavelet. The wavelet is obtained from the scaling function as N where N is an even integer. The set of wavelets then forms an orthonormal basis which we use to decompose the signal. Note that usually only few of the coefficients ak are nonzero, which simplifies the calculations.
In the following figure, some wavelet scaling functions and wavelets are plotted. The most known family of orthonormal wavelets is the family of Daubechies. Her wavelets are usually denominated by the number of nonzero coefficients ak, so we usually talk about Daubechies 4, Daubechies 6, etc. wavelets.Roughly said, with the increasing number of wavelet coefficients the functions become smoother. See the comparison of wavelets Daubechies 4 and 20 below. Another mentioned wavelet is the simplest one, the Haar wavelet, which uses a box function as the scaling function.
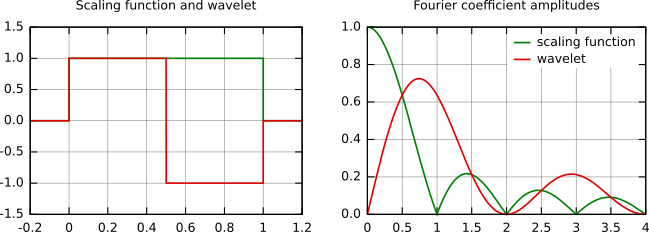
Haar scaling function and wavelet (left) and their frequency content (right).
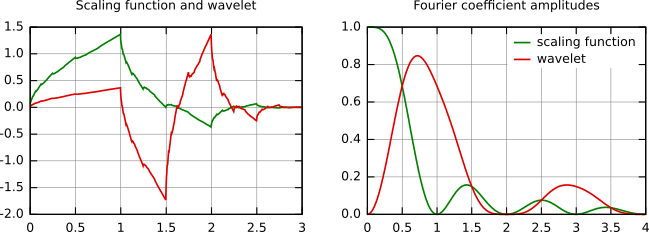
Daubechies 4 scaling function and wavelet (left) and their frequency content (right).
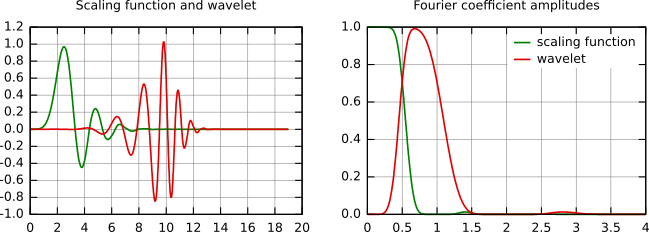
Daubechies 20 scaling function and wavelet (left) and their frequency content (right).
There are several types of implementation of the DWT algorithm. The oldest and most known one is the Mallat (pyramidal) algorithm. In this algorithm two filters – smoothing and non-smoothing one – are constructed from the wavelet coefficients and those filters are recurrently used to obtain data for all the scales. If the total number of data D = 2N is used and the signal length is L, first D/2 data at scale L/2N - 1 are computed, then (D/2)/2 data at scale L/2N - 2, … up to finally obtaining 2 data at scale L/2. The result of this algorithm is an array of the same length as the input one, where the data are usually sorted from the largest scales to the smallest ones.
Discrete wavelet transform can be used for easy and fast de-noising of a noisy signal. If we take only a limited number of highest coefficients of the discrete wavelet transform spectrum, and we perform an inverse transform (with the same wavelet basis) we can obtain more or less de-noised signal. There are several ways how to choose the coefficients that will be kept. Within Gwyddion, the universal thresholding, scale adaptive thresholding and scale and space adaptive thresholding is implemented. For threshold determination within these methods we first determine the noise variance guess given by
Where Yij corresponds to all the coefficients of the highest scale sub-band of the decomposition (where most of the noise is assumed to be present). Alternatively, the noise variance can be obtained in an independent way, for example from the AFM signal variance while not scanning. For the highest frequency sub-band (universal thresholding) or for each sub-band (for scale adaptive thresholding) or for each pixel neighborhood within sub-band (for scale and space adaptive thresholding) the variance is computed as
Threshold value is finally computed as
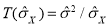
Where
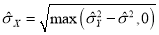
When threshold for given scale is known, we can remove all the coefficients smaller than threshold value (hard thresholding) or we can lower the absolute value of these coefficients by threshold value (soft thresholding).
DWT denoising can be accessed with
→ → .
Continuous Wavelet Transform 
Continuous wavelet transform (CWT) is an implementation of the wavelet transform using arbitrary scales and almost arbitrary wavelets. The wavelets used are not orthogonal and the data obtained by this transform are highly correlated. For the discrete time series we can use this transform as well, with the limitation that the smallest wavelet translations must be equal to the data sampling. This is sometimes called Discrete Time Continuous Wavelet Transform (DT-CWT) and it is the most used way of computing CWT in real applications.
In principle the continuous wavelet transform works by using directly the definition of the wavelet transform, i.e. we are computing a convolution of the signal with the scaled wavelet. For each scale we obtain by this way an array of the same length N as the signal has. By using M arbitrarily chosen scales we obtain a field N×M that represents the time-frequency plane directly. The algorithm used for this computation can be based on a direct convolution or on a convolution by means of multiplication in Fourier space (this is sometimes called Fast Wavelet Transform).
The choice of the wavelet that is used for time-frequency decomposition is the most important thing. By this choice we can influence the time and frequency resolution of the result. We cannot change the main features of WT by this way (low frequencies have good frequency and bad time resolution; high frequencies have good time and bad frequency resolution), but we can somehow increase the total frequency of total time resolution. This is directly proportional to the width of the used wavelet in real and Fourier space. If we use the Morlet wavelet for example (real part – damped cosine function) we can expect high frequency resolution as such a wavelet is very well localized in frequencies. In contrary, using Derivative of Gaussian (DOG) wavelet will result in good time localization, but poor one in frequencies.
CWT is implemented in the CWT module that can be accessed with
→ → .
Application of Wavelets:
Wavelets are a powerful statistical tool which can be used for a wide range of applications, namely
• Signal processing
• Data compression
• Smoothing and image denoising
• Fingerprint verification
• Biology for cell membrane recognition, to distinguish the normal from the pathological membranes
• DNA analysis, protein analysis
• Blood-pressure, heart-rate and ECG analyses
• Finance (which is more surprising), for detecting the properties of quick variation of values
• In Internet traffic description, for designing the services size
• Industrial supervision of gear-wheel
• Speech recognition
• Computer graphics and multi-fractal analysis
• Many areas of physics have seen this paradigm shift, including molecular dynamics, astrophysics, optics, turbulence and quantum mechanics.
Inverse wavelet transform
Where
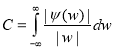
Provided
Reference
- Erwin Kreyszig, Advanced Engineering Mathematics, 9th Edition, John Wiley and amp; Sons, 2006.
- N.P. Bali and Manish Goyal, A text book of Engineering Mathematics, Laxmi Publications, Reprint, 2010.
- Veerarajan T., Engineering Mathematics (for semester III), Tata McGraw- Hill, New Delhi, 2010
- C. L. Liu, Elements of Discrete Mathematics, 2nd Ed., Tata McGraw-Hill, 2000.
