Unit – 2
Sets, relations and functions
The basic operations are:
- Union of Sets –
Union of two given sets is the smallest set which contains all the elements of both the sets.
To find the union of two given sets A and B is a set which consists of all the elements of A and all the elements of B such that no element is repeated.
The symbol for denoting union of sets is ‘∪’.
For example;
Let set A = {2, 4, 5, 6}
and set B = {4, 6, 7, 8}
Taking every element of both the sets A and B, without repeating any element, we get a new set = {2, 4, 5, 6, 7, 8}
This new set contains all the elements of set A and all the elements of set B with no repetition of elements and is named as union of set A and B.
Example: If A = {1, 3, 7, 5} and B = {3, 7, 8, 9}. Find union of two set A and B.
Solution:
A ∪ B = {1, 3, 5, 7, 8, 9}
No element is repeated in the union of two sets. The common elements 3, 7 are taken only once.
Example 2. Let X = {a, e, i, o, u} and Y = {ф}. Find union of two given sets X and Y.
Solution:
X ∪ Y = {a, e, i, o, u}
Therefore, union of any set with an empty set is the set itself.
- Intersection of sets –
Intersection of two given sets is the largest set which contains all the elements that are common to both the sets.
To find the intersection of two given sets A and B is a set which consists of all the elements which are common to both A and B.
The symbol for denoting intersection of sets is ‘∩‘.
For example:
Let set A = {2, 3, 4, 5, 6}
And set B = {3, 5, 7, 9}
In this two sets, the elements 3 and 5 are common. The set containing these common elements i.e., {3, 5} is the intersection of set A and B.
The symbol used for the intersection of two sets is ‘∩‘.
Therefore, symbolically, we write intersection of the two sets A and B is A ∩ B which means A intersection B.
The intersection of two sets A and B is represented as A ∩ B = {x: x ∈ A and x ∈ B}
Example: If A = {2, 4, 6, 8, 10} and B = {1, 3, 8, 4, 6}. Find intersection of two set A and B.
Solution:
A ∩ B = {4, 6, 8}
Therefore, 4, 6 and 8 are the common elements in both the sets.
- Complement of the Set –
In complement of a set if ξ be the universal set and A a subset of ξ, then the complement of A is the set of all elements of ξ which are not the elements of A.
Symbolically, we denote the complement of A with respect to ξ as A’.
For Example; If ξ = {1, 2, 3, 4, 5, 6, 7}
A = {1, 3, 7} find A'.
Solution:
We observe that 2, 4, 5, 6 are the only elements of ξ which do not belong to A.
Therefore, A' = {2, 4, 5, 6}
Note:
The complement of a universal set is an empty set.
The complement of an empty set is a universal set.
The set and its complement are disjoint sets.
Difference of two sets -
If A and B are two sets, then their difference is given by A - B or B - A.
• If A = {2, 3, 4} and B = {4, 5, 6}
A - B means elements of A which are not the elements of B.
i.e., in the above example A - B = {2, 3}
In general, B - A = {x : x ∈ B, and x ∉ A}
• If A and B are disjoint sets, then A – B = A and B – A = B
Example1: A = {1, 2, 3} and B = {4, 5, 6}.
Find the difference between the two sets:
(i) A and B
(ii) B and A
Solution:
The two sets are disjoint as they do not have any elements in common.
(i) A - B = {1, 2, 3} = A
(ii) B - A = {4, 5, 6} = B
Example 2: Let A = {a, b, c, d, e, f} and B = {b, d, f, g}.
Find the difference between the two sets:
(i) A and B
(ii) B and A
Solution:
(i) A - B = {a, c, e}
Therefore, the elements a, c, e belong to A but not to B
(ii) B - A = {g)
Therefore, the element g belongs to B but not A.
Example 3: Given three sets P, Q and R such that:
P = {x: x is a natural number between 10 and 16},
Q = {y: y is a even number between 8 and 20} and
R = {7, 9, 11, 14, 18, 20}
(i) Find the difference of two sets P and Q
(ii) Find Q - R
(iii) Find R - P
(iv) Find Q – P
Solution:
According to the given statements:
P = {11, 12, 13, 14, 15}
Q = {10, 12, 14, 16, 18}
R = {7, 9, 11, 14, 18, 20}
(i) P – Q = {those elements of set P which are not in set Q}
= {11, 13, 15}
(ii) Q – R = {those elements of set Q not belonging to set R}
= {10, 12, 16}
(iii) R – P = {Those elements of set R which are not in set P}
= {7, 9, 18, 20}
(iv) Q – P = {Those elements of set Q not belonging to set P}
= {10, 16, 18}
Empty Set or Null Set:
A set which does not contain any element is called an empty set, or the null set or the void set and it is denoted by ∅ and is read as phi. In roster form, ∅ is denoted by { }. An empty set is a finite set, since the number of elements in an empty set is finite, i.e., 0.
For example: (a) The set of whole numbers less than 0.
(Ans) Clearly there is no whole number less than 0.
Therefore, it is an empty set.
Singleton Set:
A set which contains only one element is called a singleton set.
For example:
• A = {x: x is neither prime nor composite}
It is a singleton set containing one element, i.e., 1.
• B = {x: x is a whole number, x < 1}
This set contains only one element 0 and is a singleton set.
Equal sets:
Two sets A and B are said to be equal if they contain the same elements. Every element of A is an element of B and every element of B is an element of A.
For example:
A = {p, q, r, s}
B = {p, s, r, q}
Therefore, A = B
Equivalent Sets:
Two sets A and B are said to be equivalent if their cardinal number is same, i.e.
n (A) = n (B). The symbol for denoting an equivalent set is ‘↔’.
For example:
A = {1, 2, 3} Here n (A) = 3
B = {p, q, r} Here n (B) = 3
Therefore, A ↔ B
Cardinal Number of a Set:
The number of distinct elements in a given set A is called the cardinal number of A. It is denoted by n (A).
For example:
• A {x: x ∈ N, x < 5}
A = {1, 2, 3, 4}
Therefore, n (A) = 4
• B = set of letters in the word ALGEBRA
B = {A, L, G, E, B, R}
Therefore, n (B) = 6
Cartesian product
Before getting with this term, let us understand what does Cartesian mean. Remember the terms used when plotting a graph paper like axes (x- axis, y-axis), origin etc. For example, (2, 3) depicts that the value on the x-plane (axis) is 2 and that for y is 3 which is not the same as (3, 2).
The way of representation is fixed that the value of the x coordinate will come first and then that for y (ordered way). Cartesian product means the product of the elements say x and y in an ordered way.
Cartesian product of Sets
The Cartesian products of sets mean the product of two non-empty sets in an ordered way. Or, in other words, the collection of all ordered pairs obtained by the product of two non-empty sets. An ordered pair means that two elements are taken from each set.
For two non-empty sets (say A&B), the first element of the pair is from one set A and the second element is taken from the second set B. The collection of all such pairs gives us a Cartesian product.
The Cartesian product of two non-empty sets A and B is denoted by A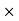 B. Also known as the cross-product or the product set of A and B. The ordered pair
B. Also known as the cross-product or the product set of A and B. The ordered pair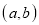 is such that
is such that 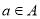 and
and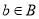 . So
. So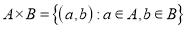 . For example, Consider two non-empty sets
. For example, Consider two non-empty sets 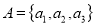 and
and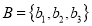 .
.
Cartesian product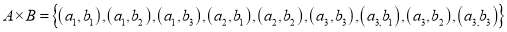 .
.
Note:
If either A or B are null sets, then A ×B will also be an empty set, i.e., if A = ∅ or
B = ∅, then A × B = ∅
For Example:
Example1. If A = {7, 8} and B = {2, 4, 6}, find A × B.
Solution:
A × B = {(7, 2); (7, 4); (7, 6); (8, 2); (8, 4); (8, 6)}
The 6 ordered pairs thus formed can represent the position of points in a plane, if a and B are subsets of a set of real numbers.
Example 2. If A × B = {(p, x); (p, y); (q, x); (q, y)}, find A and B.
Solution:
A is a set of all first entries in ordered pairs in A × B.
B is a set of all second entries in ordered pairs in A × B.
Thus A = {p, q} and B = {x, y}
Example 3. If A and B are two sets, and A × B consists of 6 elements: If three elements of
A × B are (2, 5) (3, 7) (4, 7) find A × B.
Solution:
Since, (2, 5) (3, 7) and (4, 7) are elements of A × B.
So, we can say that 2, 3, 4 are the elements of A and 5, 7 are the elements of B.
So, A = {2, 3, 4} and B = {5, 7}
Now, A × B = {(2, 5); (2, 7); (3, 5); (3, 7); (4, 5); (4, 7)}
Thus, A × B contain six ordered pairs.
Example 4. If A = {1, 3, 5} and B = {2, 3}, then
Find: (i) A × B (ii) B × A (iii) A × A (iv) (B × B)
Solution:
A ×B={1, 3, 5} × {2,3} = [{1, 2},{1, 3},{3, 2},{3, 3},{5, 2},{5, 3}]
B × A = {2, 3} × {1, 3, 5} = [{2, 1},{2, 3},{2, 5},{3, 1},{3, 3},{3, 5}]
A × A = {1, 3, 5} × {1, 3, 5}= [{1, 1},{1, 3},{1, 5},{3, 1},{3, 3},{3, 5},{5, 1},{5, 3},{5, 5}]
B × B = {2, 3} × {2, 3} = [{2, 2},{2, 3},{3, 2},{3, 3}]
What is a disjoint set?
A pair of sets which does not have any common element are called disjoint sets. For example, set 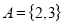 and set
and set  are disjoint sets. But set
are disjoint sets. But set 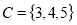 and
and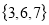 are not disjoint as both the sets C and D are having 3 as a common element. The Venn diagram of a disjoint set is given here:
are not disjoint as both the sets C and D are having 3 as a common element. The Venn diagram of a disjoint set is given here:
Another definition of disjoint sets is: when the intersection of two sets is a null or empty set then they are called disjoint sets then;
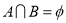
Definition of disjoint sets can be extended further to a family sets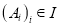 : the family is disjoint if
: the family is disjoint if 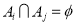 whenever
whenever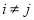 . When coming to the notation for families, it can be defined as the notion of pairwise disjoint or mutually disjoint is sometimes defined in a subtly different manner, in that repeated identical members are allowed.
. When coming to the notation for families, it can be defined as the notion of pairwise disjoint or mutually disjoint is sometimes defined in a subtly different manner, in that repeated identical members are allowed.
State whether 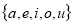 and
and 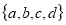 are disjoint sets or not.
are disjoint sets or not.
Solution: Suppose, 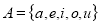 and
and 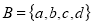
Now we have to find the intersection of the two sets, such as;
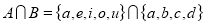
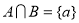
Since the intersection of the two sets does not result in a null set, therefore, 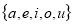 and
and are not disjoint sets.
are not disjoint sets.
Problems on Disjoint Sets
Q 1: Show that 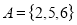 and set
and set 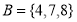 are disjoint sets.
are disjoint sets.
Solution: Given
Set 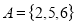
Set 
To prove: Set A and Set B are disjoint.
Proof: Two sets are disjoint if their intersection results to the null set.
Therefore,
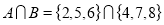
As you can see, A and B do not have any common element.
So, 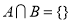
Hence proved A and B are disjoint.
Q 2: Are set 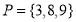 and set
and set 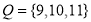 disjoint sets? If no justify your answer
disjoint sets? If no justify your answer
Solution: set 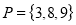
Set 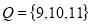
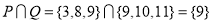
Since the intersection of the two sets P and Q results to a common element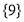 , therefore P and Q are not disjoint sets.
, therefore P and Q are not disjoint sets.
Disjoint Set Union
A disjoint set union is a binary operation on two sets. The elements of any disjoint union can be described in terms of ordered pair as  where j is the index that represents the origin of the element
where j is the index that represents the origin of the element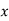 . With the help of this operation, we can join all the different (distinct) elements of a pair of sets.
. With the help of this operation, we can join all the different (distinct) elements of a pair of sets.
A disjoint union may indicate one of two conditions. Most commonly, it may intend the union of two or more sets that are disjoint. Else if they are disjoint, then their disjoint union may be produced by adjusting the sets to obtain them disjoint before forming the union of the altered sets. For example, two sets may be presented as a disjoint set by exchanging each element by an ordered pair of the element and a binary value symbolising whether it refers to the first or second set. For groups of more than two sets, one may likewise substitute each element by an ordered pair of the element and the list of the set that contains it.
The disjoint union is denoted as 
Assume that,
The disjoint union of sets 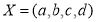 and
and 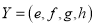 is as follows:
is as follows:
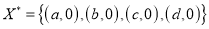 and
and 
Then
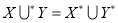
Therefore, the disjoint union set is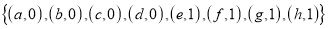 .
.
Power sets:
We have defined a set as a collection of its elements so, if S is a set then the collection or family of all subsets of S is called the power set of S and it is denoted by P(S).
Thus, if S = a, b then the power set of S is given by P(S) = {{a}, {b}, {a, b}, ∅}
We have defined a set as a collection of its elements if the element be sets themselves, then we have a family of set or set of sets.
Thus, A = {{1}, {1, 2, 3}, {2}, {1, 2}} is a family of sets.
The null set or empty set having no element of its own is an element of the power set; since, it is a subset of all sets. The set being a subset of it-self is also as an element of the power set.
For example:
Example 1: The collection of all subsets of a non-empty set S is a set of sets. Thus, the power set of a given set is always non-empty. This set is said to be the power set of S and is denoted by P(S). If S contains N elements, then P(S) contains 2^n subsets, because a subset of P(S) is either ∅ or a subset containing r elements of S, r = 1, 2, 3…
Let S = {1, 2, 3} then the power set of S is given by P(S) = {{1}, {2}, {3}, {1, 2}, {2, 3}, {1, 3}, ∅, S}.
Example 2: If S = (a), then P(S) = {(a), ∅}; if again S = ∅, then P(S) = {∅}. It should be notated that ∅ ≠ {∅}. If S = {1, 2, 3} then the subset of S {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}, ∅.
Hence, P(S) = {{1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}, ∅}.
Example 3: We know, since a set formed of all the subset of a set M as its elements is called a power set of M and is symbolically denoted by P (M). So, if M is a void set ∅, then P(M) has just one element ∅ then the power set of M is given by P(M) = {∅}
Example:
For a set  let us calculate the subsets-
let us calculate the subsets-
Subsets with 0 elements - 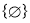 {the empty set}
{the empty set}
Subsets with 1 element - 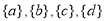
Subsets with 2 elements - 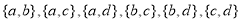
Subsets with 3 elements - 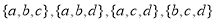
Subsets with 4 elements - 
Hence, 
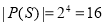
Types of Relations
Empty Relation
An empty relation (or void relation) is one in which there is no relation between any elements of a set. For example, if set 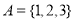 then, one of the void relations can be
then, one of the void relations can be 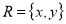 where,
where, 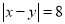 . For empty relation
. For empty relation
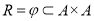
Universal Relation
A Universal (or full relation) is a type of relation in which every element of a set is related to each other. Consider set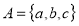 . Now one of the universal relations will be
. Now one of the universal relations will be 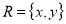 where,
where,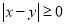 . For universal relation,
. For universal relation,
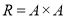
Identity Relation
In an identity relation, every element of a set is related to itself only. For example, in a set , the identity relation will be
, the identity relation will be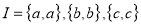 . For Identity relation,
. For Identity relation,

Inverse Relation
Inverse relation is seen when a set has elements which are inverse pairs of another set. For example, if set  then the inverse relation will be
then the inverse relation will be . So for an inverse relation
. So for an inverse relation
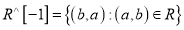
Reflexive Relation
In a reflexive relation, every element maps to itself. For example, consider a set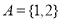 . Now an example of reflexive relation will be
. Now an example of reflexive relation will be . The reflexive relation is given by-
. The reflexive relation is given by-

Symmetric Relation
In a symmetric relation, if 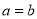 is true then
is true then 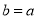 is also true. In other words, a relation R is symmetric only if
is also true. In other words, a relation R is symmetric only if 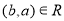 is true when
is true when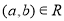 . An example of symmetric will be
. An example of symmetric will be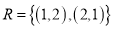 for a set
for a set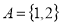 . So, for a symmetric relation
. So, for a symmetric relation

Transitive Relation
For a transitive relation, if , then
, then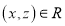 . For a transitive relation,
. For a transitive relation,
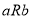 and
and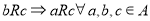 .
.
Equivalence Relation
If a relation is reflexive, symmetric and transitive at the same time it is known as an equivalence relation.
For Example
Consider a set A containing elements as {1, 2, 3} and set B contains elements as
{2, 4, 6}.
Then the relation between Set A and B from A to B will be set of any combinations from Set A to set B.
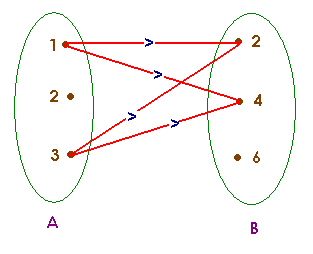
From the above diagram, we can see that Relation from A to B i.e. R will be set of {(1, 4). (1, 2), (3, 4), (3, 2)}. This relation is a subset of the Cartesian product of two sets A X B.
Let’s take another example where, set A = {1, 2, 3} and set B = {1, 2, 3, 4, 5, 6, 7, 8, 9}.
If the Relation between A and B is as: elements of B is the squares of elements of set A, then the relation is written in the form of sets as:
R = {(a, b): where b is square of a and a ∈ A & b ∈ B}
Then R = {(1, 1), (2, 4), (3, 9)}
Example: 1 A is {2, 3, 5}
B is {1, 4, 9, 25, 30}
If a R b → b is square of a
Discrete element of relation are {(2, 4), (3, 9). (5, 25)}
Example: 2 A = {Jaipur, Lucknow, Kanpur, Bhopal}
B = {Rajasthan, Uttar Pradesh, Madhya Pradesh}
ARb → a is capital of b,
A X B = {(Jaipur, Rajasthan), (Lucknow, Uttar Pradesh), (Bhopal, Madhya Pradesh}
Inverse of a Relation
Inverse of Ordered pairs
Relation : 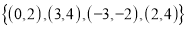
Inverse : 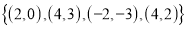
Swap ordered pairs:
If your function is defined as a list of ordered pairs, simply swap the x and y values. Remember the inverse relation will be a function only if the original function is one-to-one.
Example 1:
Given function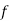 , find the inverse relation. Is the inverse relation also a function?
, find the inverse relation. Is the inverse relation also a function?

Answer:
Given function 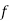 is a one-to-one function since the
is a one-to-one function since the  and
and 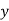 values are used only once. Sice function
values are used only once. Sice function 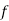 is a one-to-one function. The inverse relation is also a function. Therefore, the inverse function is
is a one-to-one function. The inverse relation is also a function. Therefore, the inverse function is
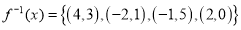
Example 2:
Determine the inverse of this function. Is the inverse also a function?
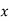 | 1 | -2 | -1 | 0 | 2 | 3 | 4 | -3 |
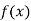 | 2 | 0 | 3 | -1 | 1 | -2 | 5 | 1 |
Answer:
Swap the x and y variables to create the inverse relation. The inverse relation will be the set of ordered pairs:
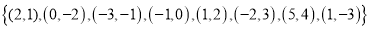
Since function 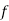 was not a one-to-one function (the y value of 1 was used twice), the inverse relation will not be a function (because the x value of 1 now gets mapped to two separate y values which is not possible for functions).
was not a one-to-one function (the y value of 1 was used twice), the inverse relation will not be a function (because the x value of 1 now gets mapped to two separate y values which is not possible for functions).
Solve algebraically:
Solving for an inverse relation algebraically is a three step process:
- Set the function
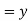
- Swap the x and y variables
- Solve for y
Example 1:
Find the inverse of the function 
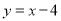 Remember:
Remember:
 Set
Set
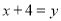 Swap the variables;
Swap the variables;
Solve for y
 You can use the inverse function notation since
You can use the inverse function notation since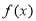 is a one-to-one function.
is a one-to-one function.
Example 2:
Find the inverse of the function (given that x is not equal to 0).
(given that x is not equal to 0).
Answer:
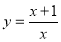 Remember: Set
Remember: Set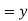 :
:
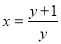 Swap the variables.
Swap the variables.
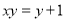
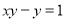 Eliminate the fraction by multiplying each side by y.
Eliminate the fraction by multiplying each side by y.
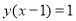 Get the y’s on side of the equal sign by subtracting y from each side. Isolate the y by factoring out the y.
Get the y’s on side of the equal sign by subtracting y from each side. Isolate the y by factoring out the y.
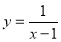 Solve for y.
Solve for y.
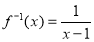 You can use the inverse function notation since f(x) is a one-to-one function.
You can use the inverse function notation since f(x) is a one-to-one function.
Example 3:
Given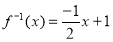 , express the equation of f(x).
, express the equation of f(x).
Answer:
At first glance, this question may look like a completely different type of problem, but it is not. Apply the same strategy that was used in Example 1. (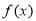 is actually the inverse of
is actually the inverse of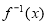 .)
.)
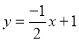

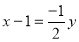 (Multiply both sides by - 2)
(Multiply both sides by - 2)
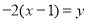

Graph:
The graph of an inverse relation is the reflection of the original graph over the identity line, .
.
It may be necessary to restrict the domain on certain functions to guarantee that the inverse relation is also a function.
Example 1:
Graph the inverse of 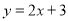
Consider the straight line,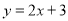 , as the original function. It is drawn in blue.
, as the original function. It is drawn in blue.
If reflected over the identity line, 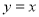 , the original function becomes the red dotted graph. The new red graph is also a straight line and passes the vertical line test for functions. The inverse relation of
, the original function becomes the red dotted graph. The new red graph is also a straight line and passes the vertical line test for functions. The inverse relation of is also a function.
is also a function.
Not all graphs produce an inverse relation which is also a function.
The following differential equation is useful in certain problems in electrical engineering.
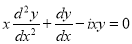 …. (1)
…. (1)
Its solutions 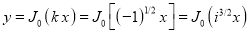
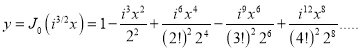
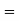

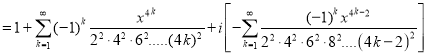
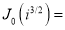 Ber (Bessel real) + Bei (Bessel imaginary)
Ber (Bessel real) + Bei (Bessel imaginary)
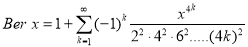
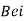
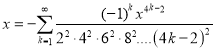
Example.
Show that 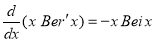
Solution:
We know that
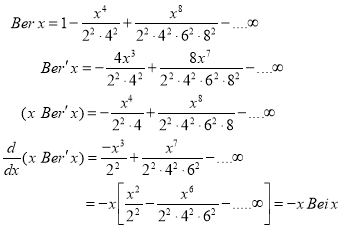
Example:
Show that 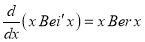
Solution
We know that 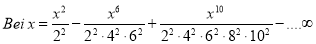 … (1)
… (1)
On differentiating (1) w.r.t ‘x’ we get
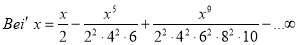
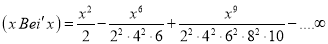


Example:
Show that 
Solution:
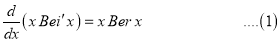
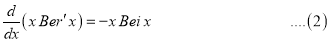
Multiplying (1) by 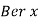 and (2)
and (2) and subtracting, we get
and subtracting, we get
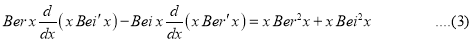
Integrating both sides of (3) from 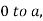 we get
we get
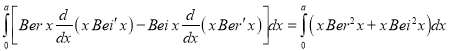
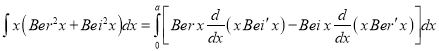
On adding and subtracting 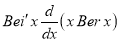 on R.H.S
on R.H.S
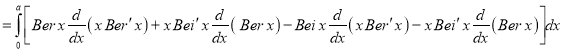

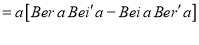
Hence proved.
Definition
A recurrence relation is an equation that recursively defines a sequence where the next term is a function of the previous terms (Expressing 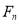 as some combination of
as some combination of 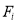 with
with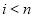 )
)
Example – Fibonacci series , Tower of Hanoi –
, Tower of Hanoi – 
Linear recurrence relations
A Linear recurrence equation of degree k or order k is a recurrence equation which is in the format 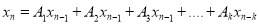
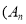 is a constant and
is a constant and 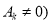 on a sequence of numbers as a first –degree polynomial.
on a sequence of numbers as a first –degree polynomial.
There are some examples of linear recurrence equations.
Recurrence relations | Initial values | Solutions |
 |  | Fibonacci number |
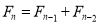 | 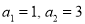 | Lucas Number |
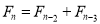 | 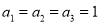 | Padovan sequence |
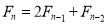 |  | Pell number |
How to solve linear recurrence relation
Suppose, a two ordered linear recurrence relation is -  where A and B real numbers.
where A and B real numbers.
The characteristic equation for the above recurrence relation is-
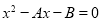
Three cases may occur while finding the roots-
Case 1 – If this equation factors as 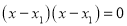 and it produces two distinct real roots
and it produces two distinct real roots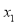 and
and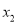 , then
, then  is the solution. [Here a and b are constants]
is the solution. [Here a and b are constants]
Case 2 – If this equation factors as 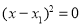 and it produces single real root
and it produces single real root 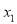 then
then is the solution.
is the solution.
Case 3 – If the equation produces two distinct complex roots, 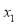 and
and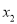 in polar form
in polar form and
and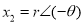 , then
, then 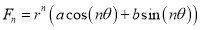 is the solution.
is the solution.
Problem 1:
Solve the recurrence  where
where 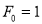 and
and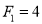
Solution
The characteristic equation of the recurrence relation is

So, 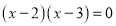
Hence the roots are  and
and 
The roots are real and distinct. So, this is in the form of case 1
Hence the solution is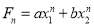
Here, 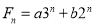 (As
(As 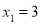 and
and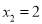 )
)
Therefore,
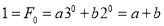
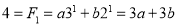
Solving these two equations, we get 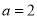 and
and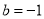
Hence the final solution is -
Problem 2:
Solve the recurrence relation -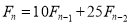 where
where  and
and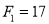
Solution:
The characteristic equation of the recurrence relation is 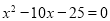
So 
Hence there is single real root 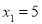
As there is single real valued root, this is in the form of case 2
Hence the solution is - 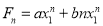
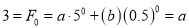
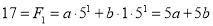
Solving these two equations, we get 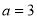 and
and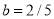
Hence the final solution is 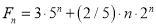
Problem 3:
Solve the recurrence relation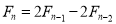 where
where and
and 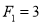
Solution
The characteristic equation of the recurrence relation is -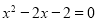
Hence the roots are 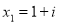 and
and 
In polar form,
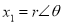 and
and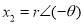 , where
, where  and
and 
The roots are imaginary so, this is in the form of case 2.
Hence the solution is
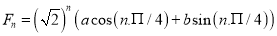

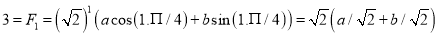
Solving these equations, we get 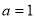 and
and 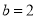
Hence the final solution is 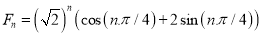
Orthogonality is a system design property which guarantees that modifying the technical effect produced by a component of a system neither creates nor propagates side effects to other components of the system.
In Euclidean geometry, orthogonal objects are related by their perpendicularity to one another. Lines or line segments that are perpendicular at their point of intersection are said be related orthogonally. Similarly, two vectors are considered orthogonal if they form a 90-degree angle.
Orthogonality property 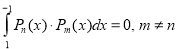 and
and 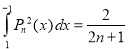
Proof: 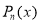 is a solution of
is a solution of  …. (1)
…. (1)
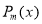 is the solution of
is the solution of 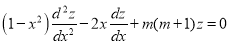 …. (2)
…. (2)
Multiplying (1) by z and (2) by y and subtracting, we get
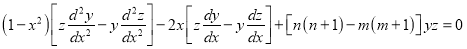
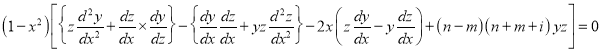

Now integrating from -1 to 1, we get
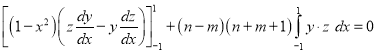

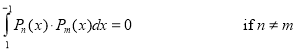
Example 1:
Prove that 
Solution: We know that 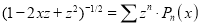
Squaring both sides we get
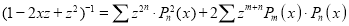
Integrating both sides between -1 and 1, we have
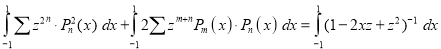
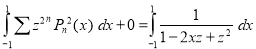
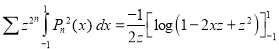
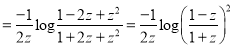
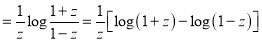

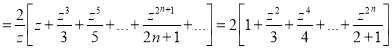
Equating the coefficient of 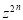 on both sides, we have
on both sides, we have
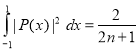
Hence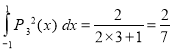
Example 2:
Assuming that a polynomial  of degree n can be written as
of degree n can be written as
 . Show that
. Show that 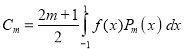
Solution:
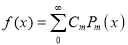
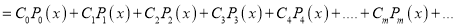
Multiplying both sides by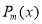 , we get
, we get
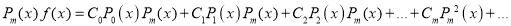



Example 3:
Using the Rodrigue’s formula for Legendre function, prove that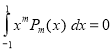 , where m, n are positive integers and
, where m, n are positive integers and 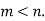
Solution:


On integrating by parts we get

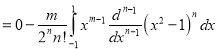
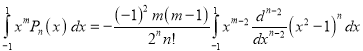
Integrating 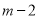 times, we get
times, we get
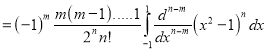
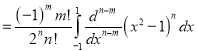
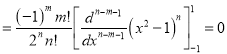
Reference
- Erwin Kreyszig, Advanced Engineering Mathematics, 9th Edition, John Wiley and amp; Sons, 2006.
- N.P. Bali and Manish Goyal, A text book of Engineering Mathematics, Laxmi Publications, Reprint, 2010.
- Veerarajan T., Engineering Mathematics (for semester III), Tata McGraw- Hill, New Delhi, 2010
- C. L. Liu, Elements of Discrete Mathematics, 2nd Ed., Tata McGraw-Hill, 2000.