Unit – 3
Introduction to Graphs
What is a Graph?
A graph is a pictorial representation of a set objects where some pairs of objects are connected by links, the interconnected objects are represented by points termed as vertices and the links that connect the vertices are called edges.
Formally, a graph is a pair of sets 
where V is the set of vertices and E is the set of edges, connecting the pairs of vertices. Take a look at the following graph
In the above graph,
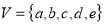
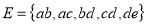
A graph is a diagram of points and lines connected to the points. It has at least one line joining a set of two vertices with no vertex connecting itself. The concept of graphs in graph theory stands up on some basic terms such as point, line, vertex, edge, degree of vertices, properties of graphs, etc. Here in this chapter we will cover these fundamentals of graph theory.
Point
A Point is particular position in a one dimensional, two-dimensional or three-dimensional space. For better understanding, a point can be denoted by an alphabet. It can be represented with a dot.
Example
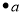
Here, the dot is a point named ‘a’
Edge
An edge is the mathematical term for a line that connects two vertices. Many edges can be formed from a single vertex. Without a vertex, and edge cannot be formed. There must be a starting vertex and an ending vertex for an edge.
Example
Here, ‘a’ and ‘b’ are the two vertices and the link between them is called an edge.
Graph
A graph ‘G’ is defined as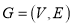 
where V is a set of all vertices and E is a set of all edges in the graph.
Example 1:
In the above example ab, ac, cd and bd are the edges of the graph. Similarly a, b, c and d are the vertices of the graph.
Line:
A Line is a connection between points. It can be represented with a solid line.
Example:
Here, ‘a’ and ‘b’ are the points. The link between these two points is called a line.
Vertex
A Vertex is a point where multiple lines meet. It is also called a node. Similar to points, a vertex is also denoted by an alphabet.
Example
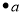
Here, the vertex is named with an alphabet ‘a’.
Example 2:
In this graph, there are four vertices a, b, c, and d and four edges ab, ac, ad and cd.
Loop
In a graph, if an edge is drawn from vertex to itself it is called a loop.
Example 1:
In the above, V is a vertex for which it has an edge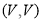 
forming a loop
Example 2
In this graph, there are two loops which are formed at vertex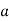 
, and vertex 
.
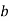Degree of vertex
It is the number of vertices adjacent to a vertex V
Notation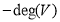
In a simple graph with n number of vertices, the degree of any vertices is
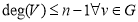
A vertex can form an edge with all other vertices except by itself. So the degree of a vertex will be up to the number of vertices in the graph minus 1. This 1 is for the self-vertex as it cannot form a loop by itself. If there is a loop at any of the vertices, then it is not a Simple Graph.
Degree of vertex can be considered under two cases of graphs-
- Undirected Graph
- Directed Graph
Degree of Vertex in an Undirected Graph
An undirected graph has no directed edges. Consider the following examples.
Example 1
Take a look at the following graph
In the above undirected Graph,
, as there are 2 edges meeting at vertex ‘a’
, as there are 3 edges meeting at vertex ‘b’
, as there is 1 edge formed at vertex ‘c’- So ‘c’ is pendent vertex.
, as there are 2 edges meeting at vertex‘d’.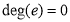
, as there are 0 edges formed at vertex ‘e’.
Example 2:
Take a look at the following graph-
In the above graph,
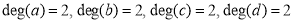and 
The vertex ‘e’ is an isolated vertex. The graph does not have any pendent vertex.
Degree of vertex in a Directed Graph
In a directed graph each vertex has an indegree and an outdegree.
Indegree of a graph
- Indegree of vertex V is the number of edges coming into the vertex V.
- Notation -
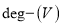
Outdegree of a Graph
- Outdegree of vertex V is the number of edges which are going out from the vertex V
- Notation
Example 1
Take a look at the following directed graph. Vertex ‘a’ has two edges, ‘ad’ and ‘ab’, which are going outwards. Hence its outdegree is 2. Similarly, there is an edge ‘ga’, coming towards vertex ‘a’. Hence the indegree of ‘a’ is 1.
The indegree and outdegree of other vertices are shown in the following table-
Vertex | Indegree | Outdegree |
a | 1 | 2 |
b | 2 | 0 |
C | 2 | 1 |
d | 1 | 1 |
e | 1 | 1 |
f | 1 | 1 |
g | 0 | 2 |
Example 2:
Take a look at the following directed graph. Vertex ‘a’ has an edge ‘ae’ going outwards from vertex ‘a’. Hence its outdegree is 1. Similarly, the graph has an edge ‘ba’ coming towards vertex ‘a’. Hence the indegree of ‘a’ is 1.
The indegree and outdegree of other vertices are shown in the following table-
Vertex | Indegree | Outdegree |
a | 1 | 1 |
b | 0 | 2 |
C | 2 | 0 |
d | 1 | 1 |
e | 1 | 1 |
Basic properties of graph:
Graphs come with various properties which are used for characterization of graphs depending on their structures. These properties are defined in specific terms pertaining to the domain of graph theory. In this chapter, we will discuss a few basic properties that are common in all graphs.
1. Distance between Two Vertices
It is number of edges in a shortest path between Vertex U and Vertex V. If there are multiple paths connecting two vertices, then the shortest path is considered as the distance between the two vertices.
Notation − d (U, V)
There can be any number of paths present from one vertex to other. Among those, you need to choose only the shortest one.
Example
Take a look at the following graph-
Here, the distance from vertex‘d’ to vertex ‘e’ or simply ‘de’ is 1 as there is one edge between them. There are many paths from vertex‘d’ to vertex ‘e’-
- Da, ab, be
- Df, fg, ge
- De (It is considered for distance between the vertices
- Df, fc, ca, ab, be
- Da, ac, cf, fg, ge
2. Eccentricity of a Vertex
The maximum distance between a vertex to all other vertices is considered as the eccentricity of vertex.
Notaion – e(V)
The distance from a particular vertex to all other vertices in the graph is taken and among those distances, the eccentricity is the highes of distances.
Example
In the above graph, the eccentricity of ‘a’ is 3.
The distance from ‘a’ to ‘b’ is 1 (ab’)
From ‘a’ to ‘c’ is 1(‘ac’),
From ‘a’ to ‘d’ is 1 (‘ad’),
From ‘a’ to ‘e’ is 2 (‘ab’-’be’) or (‘ad’-’de’),
From ‘a’ to ‘f’ is 2 (‘ac’-‘cf’) or (‘ad’-‘df’),
From ‘a’ to ‘g’ is 3 (‘ac’-‘cf’-‘fg’) or (‘ad’-‘df’-‘fg’)
So the eccentricity is 3, which is a maximum from vertex ‘a’ from the distance between ‘ag’ which is maximum.
In other words,
e(b) =3
e(c) =3
e (d) =3
e(e) =3
e(f)=3
e(g)=3
3. Radius of a Connected Graph
The minimum eccentricity from all the vertices is considered as the radius of the Graph G. The minimum among all the maximum distances between a vertex to all other vertices is considered as the radius of the Graph G.
Notation − r (G)
From all the eccentricities of the vertices in a graph, the radius of the connected graph is the minimum of all those eccentricities.
Example
In the above graph r (G) = 2, which is the minimum eccentricity for‘d’.
4. Diameter of a Graph
The maximum eccentricity from all the vertices is considered as the diameter of the Graph G. The maximum among all the distances between a vertex to all other vertices is considered as the diameter of the Graph G.
Notation − d (G) − from all the eccentricities of the vertices in a graph, the diameter of the connected graph is the maximum of all those eccentricities.
Example
In the above graph, d (G) = 3; which is the maximum eccentricity.
5. Central Point
If the eccentricity of a graph is equal to its radius, then it is known as the central point of the graph. If
e (V) = r (V),
Then ‘V’ is the central point of the Graph ’G’.
Example
In the example graph,‘d’ is the central point of the graph.
e (d) = r(d) = 2
6. Centre
The set of all central points of ‘G’ is called the centre of the Graph.
Example
In the example graph, {‘d’} is the centre of the Graph.
7. Circumference
The number of edges in the longest cycle of ‘G’ is called as the circumference of ‘G’.
Example
In the example graph, the circumference is 6, which we derived from the longest cycle a-c-f-g-e-b-a or a-c-f-d-e-b-a.
8. Girth
The number of edges in the shortest cycle of ‘G’ is called its Girth.
Notation: g (G).
Example − In the example graph, the Girth of the graph is 4, which we derived from the shortest cycle a-c-f-d-a or d-f-g-e-d or a-b-e-d-a.
9. Sum of Degrees of Vertices Theorem
If G = (V, E) be a non-directed graph with vertices V = {V1, V2,…Vn} then
n Σ i=1 deg (Vi) = 2|E|
Corollary 1
If G = (V, E) be a directed graph with vertices V = {V1, V2,…Vn}, then
n Σ i=1 deg+(Vi) = |E| = n Σ i=1 deg− (Vi)
Corollary 2
In any non-directed graph, the number of vertices with Odd degree is Even.
Corollary 3
In a non-directed graph, if the degree of each vertex is k, then
k|V| = 2|E|
Corollary 4
In a non-directed graph, if the degree of each vertex is at least k, then
k|V| ≤ 2|E|
| Corollary 5
In a non-directed graph, if the degree of each vertex is at most k, then
k|V| ≥ 2|E|
A graph is traversable if you can draw a path between all the vertices without retracing the same path. Based on this path, there are some categories like Euler’s path and Euler’s circuit which are described as -
Euler’s Path
An Euler’s path contains each edge of ‘G’ exactly once and each vertex of ‘G’ atleast once A conncected graph G is said to be traversible if it contains an Euler’s path.
Example
Euler’s Path=d-c-a-b-d-e.
Euler’s Circuit
In a Euler’s path, if the starting vertex is same as its ending vertex, then it is called an Euler’s circuit.
Example
Euler’s Circuit Theorem
A connected graph ‘G’ is traversable if and only if the number of vertices with odd degree in G is exactly 2 or 0. A connected graph G can contain an Euler’s path, but not an Euler’s circuit if it has exactly two vertices with an odd degree.
Note: This Euler path begins with a vertex odd degree and ends with other vertex of odd degree.
Euler’s path – b-e-a-b-d-c-a is not an Euler’s circuit, but it is an Euler’s path. Clearly it has exactly 2 odd degree vertices.
Note: In a connected graph G, if the number of vertices with odd degree=0, then Euler’s circuit exists.
Hamiltonian Graph
A connected graph G is said to be Hamiltonian graph, if there exists a cycle which contains all the vertices of G.
Every cycle is a circuit but a circuit may contain multiple cycles. Such a cycle is called a Hamiltonian cycle of G.
Hamiltonian Path
A connected graph G is said to be Hamiltonian if it contains each vertex G exactly once. Such a path is called a Hamiltonian path.
Example
Hamiltonian path – e-d-b-a-c
Note:
- Euler’s circuit contains each edge of the graph exactly once.
- In a Hamiltonian cycle, some edges of the graph can be skipped.
Example:
Take a look at the following graph-
For the graph shown above-
- Euler path exists – false
- Euler circuit exists – false
- Hamiltonian cycle exists –true
- Hamiltonian path exists –true
G has four vertices with odd degree, hence it is not traversable. By skipping the internal edges, the graph has a Hamiltonian cycle passing through all the vertices.
Cycle graph
A simple graph with ‘n’ vertices (n>=3) and ‘n’ edges is called a cycle graph if all its edges form a cycle of length ‘n’.
If the degree of each vertex in the graph is two, then it is called a Cycle Graph.
Notation -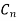 
Example
Take a look at the following graphs-
- Graph I has 3 vertices with 3 edges which is forming a cycle ‘ab-bc-ca’
- Graph II has 4 vertices with 4 edges which is forming a cycle ‘pq-qs-sr-rp’.
- Graph III has 5 vertices with 5 edges which is forming cycle ‘ij-km-ml-lj-ji’.
Hence all the given graphs are cycle graphs.
Cyclic Graph
A graph with at least one cycle is called a cyclic graph.
Example
In the above example graph, we have two cycles a-b-c-d-a and c-f-g-e-c. Hence it is called a cyclic graph.
Acyclic Graph
A graph with no cycles is called an acyclic graph.
Example:
In the above example graph, we do not have any cycles. Hence it is a non-cyclic graph.
A subgraph S of a graph G is a graph whose set of vertices and set of edges are all subsets of G. (Since every set is a subset of itself, every graph is a subgraph of itself.)
All the edges and vertices of G might not be present in S; but if a vertex is present in S, it has a corresponding vertex in G and any edge that connects two vertices in S will also connect the corresponding vertices in G.
All of these graphs are subgraphs of the first graph.
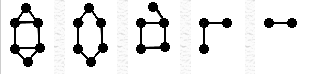
A vertex-induced subgraph is one that consists of some of the vertices of the original graph and all of the edges that connect them in the original. An edge-induced subgraph consists of some of the edges of the original graph and the vertices that are at their endpoints.
 | The second two figures are vertex-induced subgraphs of the first figure. |
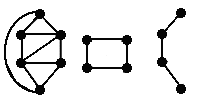 | The second two figures are edge-induced subgraphs of the first figure. |
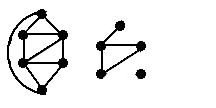 | The second figure is a subgraph of the first figure, but it is neither edge-induced nor vertex-induced. |
A spanning subgraph is a subgraph that contains all the vertices of the original graph. A spanning tree is a spanning subgraph that is often of interest. A cycle in a graph that contains all the vertices of the graph would be called a spanning cycle. However it's more common name is a Hamiltonian cycle.
Example: Graph S is a subgraph of G:
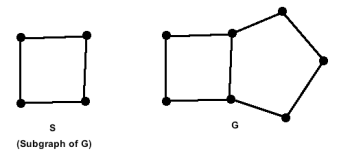
A graph can exist in different forms having the same number of vertices, edges, and also the same edge connectivity. Such graphs are called isomorphic graphs.
Isomorphic Graphs
Two graphs 
and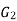 
are said to be isomorphic if
- Their number of components (vertices and edges) are same
- Their edge connectivity is retained.
Note: In short out of the two isomorphic graphs, one is a tweaked version of the other. An unlabelled also can be thought of as an isomorphic graph.
There exists a function ‘f’ from vertices of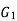 
to vertices of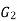 
[f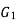 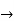: V(
) 
V(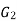
)], such that
Case (i): f is a bijection (both one-one and onto).
Case (ii): f preserves adjacency of vertices, i.e., if the edge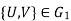
, then the edge
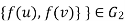, then 
Note
If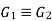 
then 
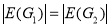
Degree sequences of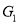 
and 
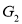are same.
If the vertices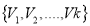 
form a cycle of length K in
, then the vertices
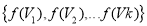should form a cycle for length K in
.
All the above conditions are necessary for the graphs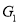 
and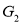 
to be isomorphic but not sufficient to prove that the graphs are isomorphic.
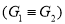If and only 
where 
and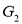 
are simple graphs.
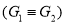If the adjacency matrices of
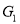and
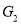are same.
If and only if the corresponding subgraphs of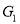 
and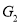 
(obtained by deleting some vertices in 
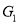and their images in graph
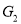) are isomorphic.
Example
Which of the following are isomorphic?
In the graph
, vertex ‘w’ has only degree 3, whereas all the other graph vertices has degree 2. Hence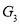
not isomorphic to 
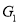or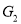
.
Taking compliments of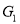 
and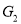
, you have
Here,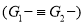 
, hence 
.
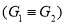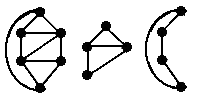
Trees are graphs that do not contain even a single cycle. They represent hierarchical structure in a graphical form. Trees belong to the simplest class of graphs. Despite their simplicity, they have a rich structure.
Trees provide a range of useful applications as simple as a family tree to as complex as trees in data structures of computer science.
Tree
A connected acyclic graph is called a tree. In other words, a connected graph with no cycles is called a tree.
The edges of a tree are known as branches. Elements of trees are called their nodes. The nodes without child nodes are called leaf nodes.
A tree with ‘n’ vertices has ‘n-1’ edges. If it has one more edge extra than ‘n-1’, then the extra edge should obviously has to pair up with two vertices which leads to form a cycle. Then it becomes a cyclic graph which is a violation for the tree graph.
Example 1
The graph shown here is a tree because it has no cycles and it is connected. It has four vertices and three edges, i.e., for ‘n’ vertices ‘n-1’ edges as mentioned in the definition.
Note – every tree has at least two vertices of degree one.
Example 2
In the above example, the vertices ‘a’ and ‘d’ has degree one. And the other two vertices ‘b’ and ‘c’ has degree two. This is possibe because for not forming a cycle, there should be at least two single edges anywhere in the graph. It is nothing but two edges with a degree of one.
Forest
A disconnected acyclic graph is called a forest. In other words, a disjoint collection of trees is called a forest.
Example
The following graph looks like two sub-graphs looks like two sub-graphs; but it is a single disconnected graph. There are no cycles in this graph. Hence, clearly it is a forest.
Spanning Trees
Let G be a connected graph, then the sub-graph H of G is called a spanning tree of G if
- H is a tree
- H contains all vertices of G
A spanning tree T of an undirected graph G is a subgraph that includes all of the vertices of G.
Example
In the above example, G is a connected graph and H is a subgraph of G.
Clearly, the graph H has no cycles, it is a tree with six degrees which is one less than the total number of vehicles. Hence H is the spanning tree of G.
Reference
- Erwin Kreyszig, Advanced Engineering Mathematics, 9th Edition, John Wiley and amp; Sons, 2006.
- N.P. Bali and Manish Goyal, A text book of Engineering Mathematics, Laxmi Publications, Reprint, 2010.
- Veerarajan T., Engineering Mathematics (for semester III), Tata McGraw- Hill, New Delhi, 2010
- C. L. Liu, Elements of Discrete Mathematics, 2nd Ed., Tata McGraw-Hill, 2000.
