Unit – 2
System modelling in terms of differential equations
Initial and Final Condition of Network
INTIAL CONDITIONS: -
Time t=0- , time t=0-1-time t= infinity
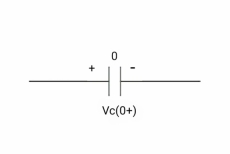
Diagram
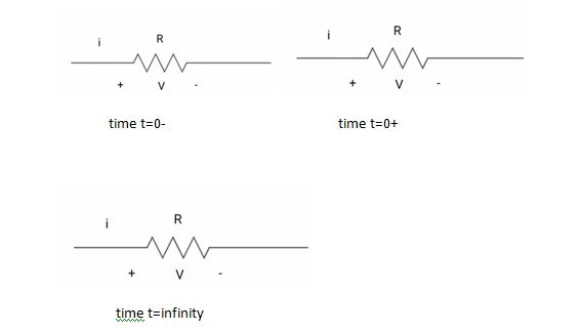
# In case of capacitor: -
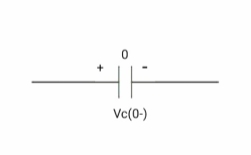
At time t= 0-
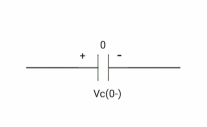
:. Capacitor is initially uncharged
Q (0-) =0
Q=cv
Q (0-) = cvc (0-)
Vc (0-) =0
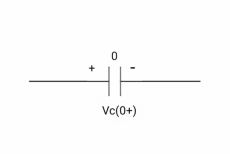
At time t= 0+
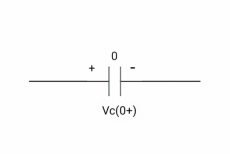
By low of conservation of charges
Q (0-) = Q (0+)
Cvc (0-) =cvc (0+)
Vc (0+) =0
Hence acts as
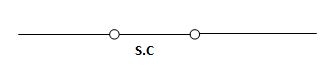
If capacitor is initially uncharged at t= 0- than voltage across capacitor is zero at t=0+ capacitor will follow low of consvation of charges and Vc (0+) =0 it means at t=0+ capacitor behaves as short circuit in other words, voltage across capacitor cannot change instantaneously.
At time t= infinity,
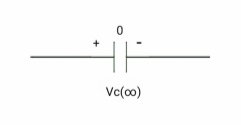
I = cdvc/dt constant and maximum
Hence, i= 0
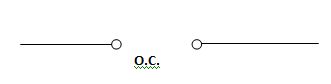
At t= infinity capacitor will be fully charged or voltage across capacitor is constant and current through capacitor is zero so, capacitor will behave as open –circuit
Say capacitor is initially charged
At time t= 0-,
At time t= 0+,
At time t= 0+
Q (0-) = Q (0+)
Cvc (0-) =cvc (0+)
V1 = Vc (0+)
Hence acts as
Its capacitor is initially charged at t= 0- as voltage across capacitor is V1 than at t=0+ capacitor behaves as a voltage as a voltage source with value V1
At time t = infinity
If capacitor is initially charged and it is connected to any independent source for long time than current through capacitor is 3 etw and capacitor will be fully charged and it behaves as o.c
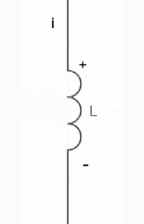
# for Inductor: -
At time t= 0-
Ø= Li =0
Ø (0) = Li (0-)
i (0-) =0
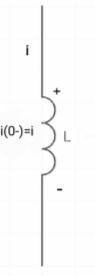
At t= 0+,
By low of conservation of flux
Ø (0-) = Ø (0+)
Li (0-) = Li (0+)
0 =i (0+)
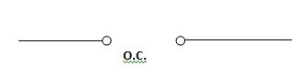
Hence, acts as short circuit
System Modelling in terms of Differential Equation:
A linear differential equation which describes any circuit has two parts in its solution, one is complimentary function and other is particular solution. The complimentary solution gives the transient response and the particular solution deals with steady state response. The complete or total response of network is the sum of the transient response and steady state response which is represented by general solution of differential equation.
First order homogenous differential equation.
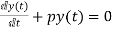
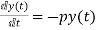
Integrating both sides
y(t)=k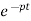
First order non homogenous differential equation
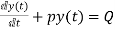
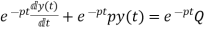
Integrating above equation we get
y(t)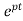 =∫ Q
=∫ Q 
y(t)= ∫ Q
∫ Q 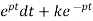
The first term of above solution is known as particular Integral and second is known as complementary function.
FOR RL Circuit
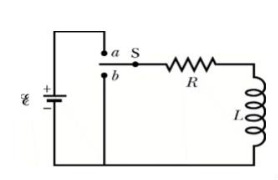
Fig: Series RL circuit
After switch is closed applying KVL
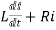 =0
=0
This is first order homogeneous differential equation so
 dt
dt
Integrating both sides
Ln i=  t+K
t+K
Taking antilog of both sides
i=k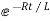
At t=0
i (0) =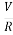 =I0
=I0
 =ke0
=ke0
The particular solution is given as
i= 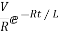 for t≥0
for t≥0
= for t<0
for t<0
FOR RC Circuit
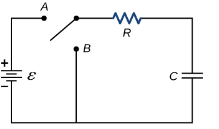
Fig: Series RC circuit
 =V
=V
For t>0 applying KVL
Ri(t)+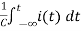 +V=0
+V=0
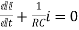
Hence general solution of above equation is calculated same as for RL circuit
i=k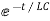
i (0) =- 
Hence, particular solution for network is given as
i=- 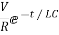 for t for t≥0
for t for t≥0
=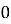 for t<0
for t<0
Time Constant
Time constant for RL circuit
From above section for RL circuit at t≥0
i= 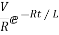
i=I0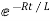
I0= 

Time taken for current to drop from unity to zero is called as time constant T.
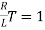
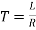 sec
sec
FOR RC Circuit
It can be calculated in the same manner as for series RL circuit
The time constant is given as 
T=RC
Que: - diagram
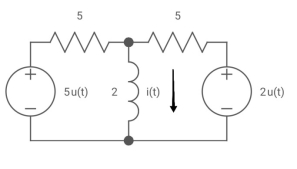
V0 (t) =? t =o if capacitor is uncharged?
Soln: - diagram
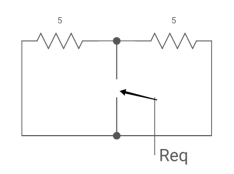
Req = R1R2 /R1+R2
V0(0) =0
V0 (infinity) = VR R2/R1+R2
V0 (t) = V0 (infinity) + [Vo (0) – V0 (infinity)] e-t/c
=VR R2/R1+R2 *[ 1- e+(R1+R2)/R1R2]
Ques
Diagram
Time constant, c= L/Req = L/R
V(infinity) = 0
V (0) = VR
I(infinity) = VR/R, I (0) =0
By KVL,
VR=i(t) R + L di/dt(t)
On solving
V0(t)= VR e-tR/L
Ques
Diagram

Find i(t)
For t>0?
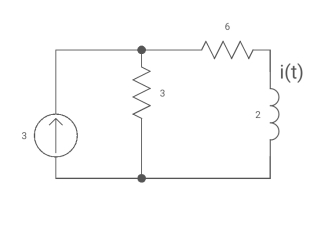
Soln
Diagram
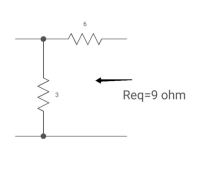
Req = 673
= 9 ohms
Diagram
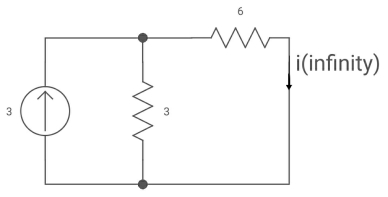
T= L/Req = 2/9 sec
I (0) =0
I(infinity) = 3*3/6+3 = 1A
i (+) = 1 [1-e4.51]
Ques
Diagram
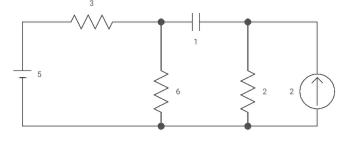
Capacitor is initially uncharged find
Vc (t); t >0
Diagram
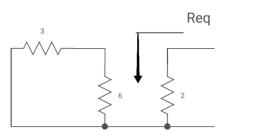
Req = (3116) +2
=2+2 = 4ohm
C= c Req
= 2 sec
Clearly Vc (0) =0
Diagram

By voltage divides, VA = 5*6/3+B = 30 v/9
Clearly by ohms low
VB = 2*2 = 4v
Apply KVL, VA-Vc-VB =0
Vc(infinity) = 30/9 – 4 = -2/3 V
Vc (t) = -2/3 [1- e0.5t]
CURVE: -
Diagram
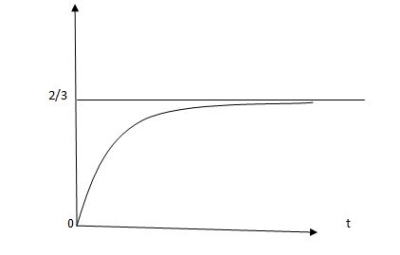
Vc(t) =2/3 [1-e-0.25]
Diagram
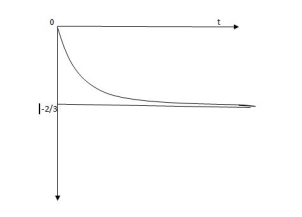
Vc(t) = -2/3 [1-e]
Ques
Diagram
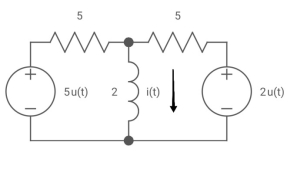
(t) =?
Soln: - we know i(t) = I (infinity) + [i (0)- i(infinity0] e-t/c
Diagram
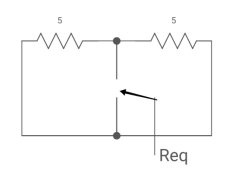
Req = 5*5/5+5 = 5?2 ohm
:. T=L/Req = 4/5 sec
Also, i (0) =0
i(infinity) = u(t) +2/5 u(t)
:. I(t) = 1.4 [1-e-5/4t)] u(t)
Transient Response Of R-L, R-C And R-L-C Network in Time Domain
The transient response means the change in the response of output with respect to time. So, using initial conditions, and solution for differential equations we solve some numerical.
Ques: Diagram

If switch ‘s’ closed at t= 0 find out the voltage across capacitor and current through capacitor at t= 0+?
Soln: at t= 0- switch was open so,
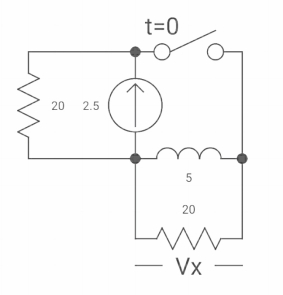
:. There is no potential so Vc (0-) = 0
At t= 0+, Vc (0-) = Vc (0+) = 0
Diagram
Isc = 10/5 = 2 A
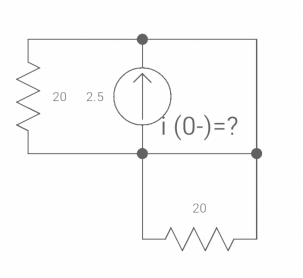
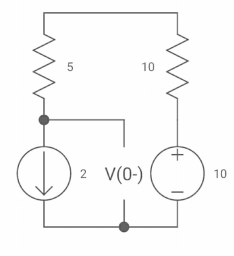
Ques: Diagram
The switch was closed for long time before
Opening at t=0- find VX (0+)?
(a) 25V (b) 50 V (c)-50V (d) 0V
Soln at time t=0-
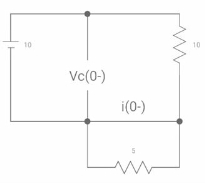
Clearly, il (0-) = 2.5 A
At t= 0+, as inductor is initially charges
So il (0-) = il (0+)
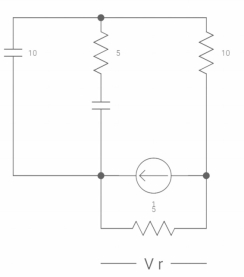
-VX= 20/2.5 20*2.5
VX= -50A
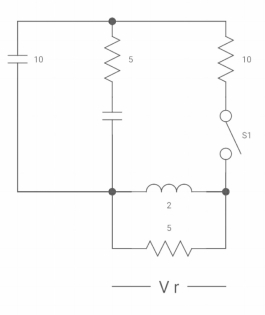
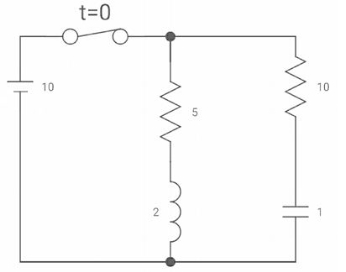
Ques:
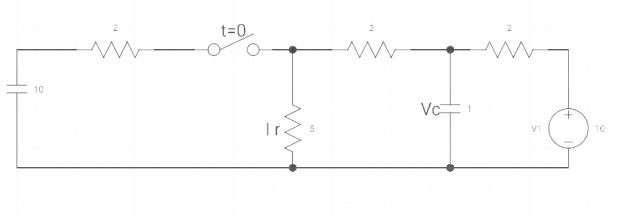
VR (0+) =
Dil/dt(t) = 0+?
If switch is opened at t= 0?
Soln: -
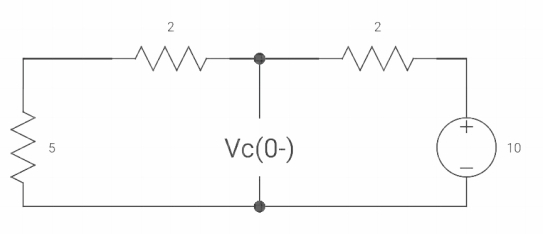
At t=0-
Vc (0-) = 10V
IL (0-) = 10/10 = 1 A
Also, iL (0-) = iL (0+) = 1A
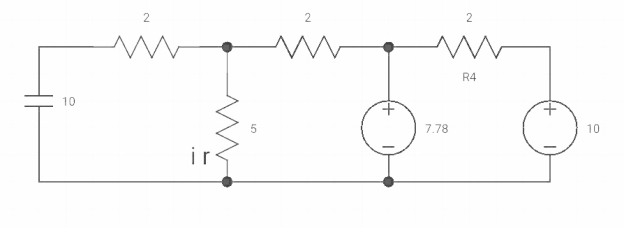
VR(0+) = 5V
Ldi(t)/dt = VL (t)
DiL(t)/dt = VL(t)/L
At t= 0+
d/dt iL (0+) = VL (0+)/L
-VL (0+)-VR =0
VL (0+) = -5V
Dt(t) at t = ot = vl (ot)/L
=-5/2
Dil/dt(o+) = 2.5 A/s
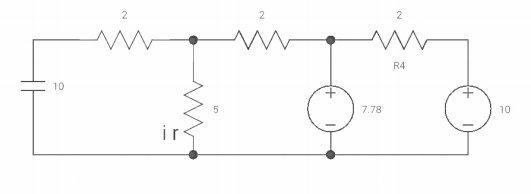
Vc(o+) and iR (o+) it switches ‘s’ is closed at t=0?
At t=0
As capacitor is fully charged so acts as
Vc (0-) = 7*10/7+2 = 70/9v
At t=0+
Vc (0+) = Vc (0) = 40/9v
By applying kcl at A,
VA-10/2+ VA/5+VA-7019/2 =0
VA [1/5+1/2+1/2] = 5+35/9
Va [6/5] = 80/9
Va= 400/54v
IR (0+) = Va/5 = 400/54*5 = 80/54 A
Exponential Rising or Decaying curve
x(t)=x (∞) + [x (0)-x (∞)]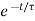
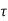 =time constant
=time constant
From above relation x(t)=0+ [1-0] =
=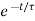
At t=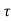 , x (
, x (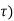 =
=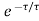 =e-1=0.367
=e-1=0.367
For exponentially decaying signal time at which magnitude of x(t) becomes 36.7% of maximum magnitude of x(t) is called time constant.
x(t)=0+ [1-0]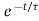 =1-
=1-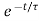
At t=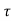
x (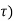 =0.632.
=0.632.
For exponentially rising signal time at which magnitude of x(t) becomes 63.2% of maximum value of x(t) is called time constant.
TRANSIENT RESPONSE :-
Total response = transient response +steady state response
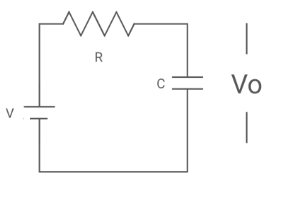
V1 –i(t) R-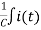 dt=0
dt=0
Differentiate
0+R +
+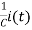 =0
=0
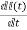 +
+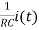 =0
=0
I.F=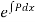
=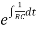 =
=
Hence solution is y(t)I. F=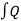 IF dx+k
IF dx+k
i(t) =k
=k
i(t)=k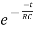
At t=0, i (0) =k=V1/R
i(t)=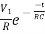
NOTE: Time constant for RC circuit=RC, and for LR circuit =L/R
V0(t)= dt=
dt=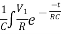 dt=V1(1-
dt=V1(1-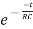 )
)
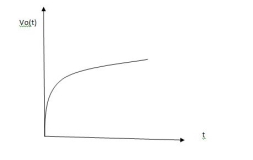
The plot for above equations is

ALTERNATE METHOD: -
i(t) = i (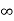 )+[ i (0)- i (
)+[ i (0)- i (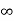 )]
)]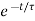
V0(t) =V0 (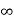 ) + [V0(0)-V0(
) + [V0(0)-V0(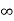 )]
)]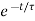
And time constant,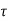 =C Req
=C Req
i(0) = V1/ R
i (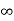 ) = 0
) = 0
V0(0) =0
V0 (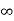 ) = V1
) = V1
Req = R, 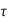 =RC
=RC
On substituting we get similar results.
Que: -
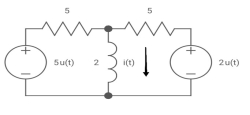
V0 (t) =? t =o if capacitor is uncharged?
Soln: - We know i(t) = i (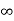 )+[ i (0)- i (
)+[ i (0)- i (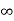 )]
)]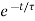
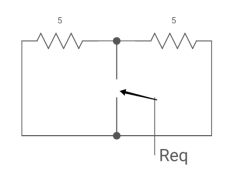
Req = R1R2 /R1+R2=(5x5)/ (5+5) =5/2ohm
 =L/Req=4/5 sec
=L/Req=4/5 sec
i (0) =0
i( )=u(t)+
)=u(t)+ u(t)=1.4u(t)
u(t)=1.4u(t)
i(t)=1.4[1-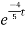 ]u(t)
]u(t)
Ques
Diagram
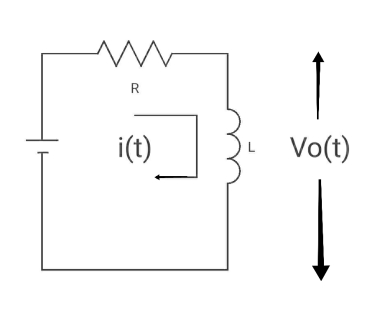
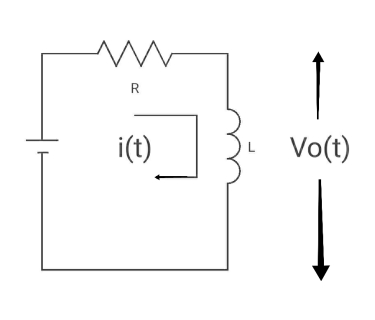
Time constant  =L/Req = L/R
=L/Req = L/R
V (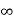 ) = 0, V (0) =VR (supply voltage)
) = 0, V (0) =VR (supply voltage)
i (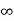 ) = VR/R, i (0) =0
) = VR/R, i (0) =0
By KVL,
VR=i(t) R + L di/dt(t)
On solving
V0(t)= VR e-tR/L
Sinusoidal Steady State Analysis:
1) The method used is phasor method.
2) Take Laplace transform of R, L and C in the circuit.
3) Make all initial conditions zero.
4) Derive the expression for desired voltage and current.
5) Replace S by jω where ω is the frequency at which the circuit is operating.
Que) If V1=6cos2t, find i2 at steady state.
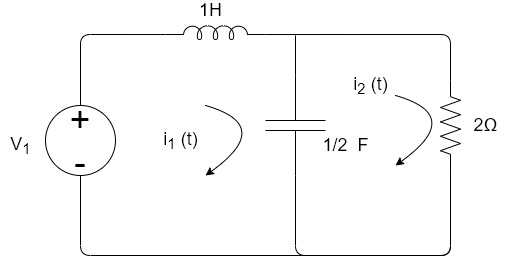
Sol: Apply KVL
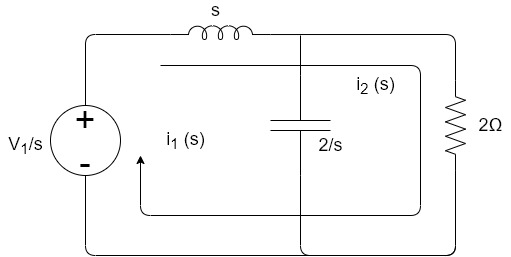
6 -sI1(s)-2I2(s)=0
-sI1(s)-2I2(s)=0
-2I2(s)-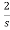 I2(s)+
I2(s)+ I1(s)=0
I1(s)=0
I2(s)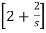 =
= I1(s)
I1(s)
I1(s)= [
[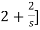 I2(s)
I2(s)
Substituting I1(s) in first equation
6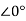 -s
-s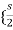 [
[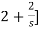 }I2(s)- 2I2(s)=0
}I2(s)- 2I2(s)=0
Solving above equation we get
I2(s)=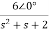
Replace s=jω, s=2j
I2(jω) = =
=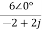 =
=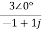
=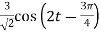
Que) If V1=2sin2t, Va at steady state will be?
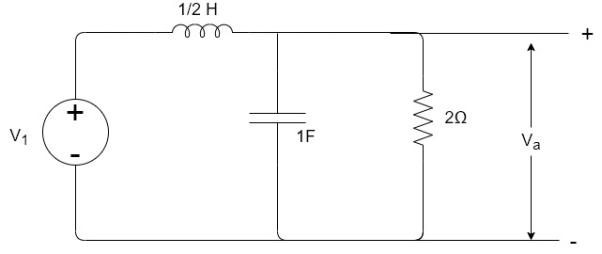
Sol: Zeq=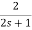
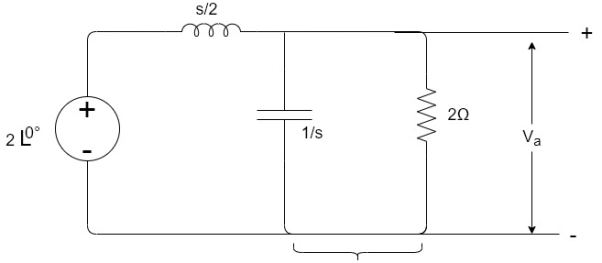
By voltage divider rule Va=
Replace s by jω , s=2j
Va=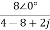 =
=
Va=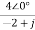 =
=
Va=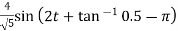
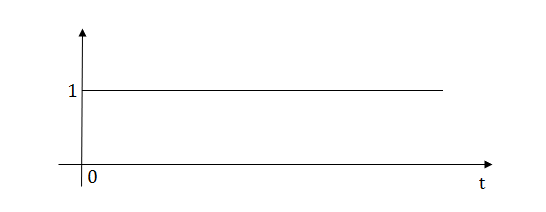
1) Step Function:
U(t)=1 t≥0
=0 t<0


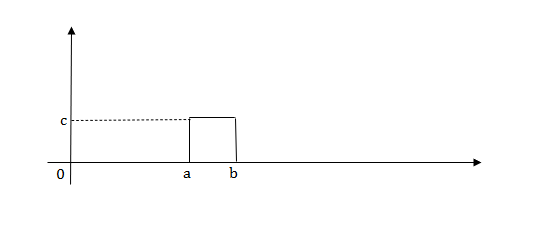
2) Pulse Function:
L[u(t)]=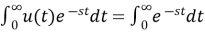 =
=
f(t)<—>F(s)
f(t-a)= F(s)
F(s)
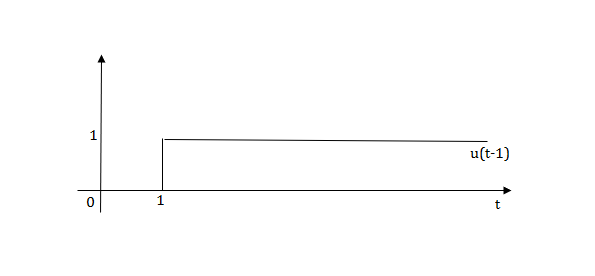
L[u(t-a)]=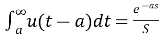
Laplace transforms of pulse


Q.1) Write equation for given waveform
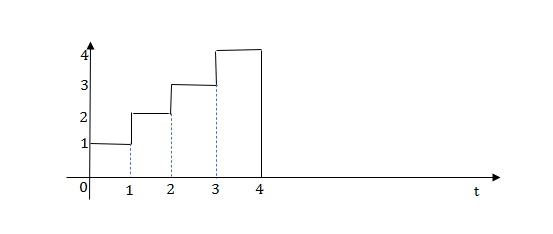
Sol: 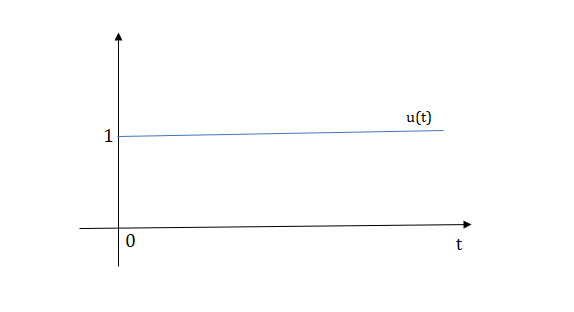
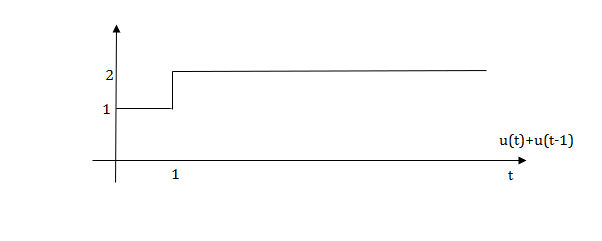
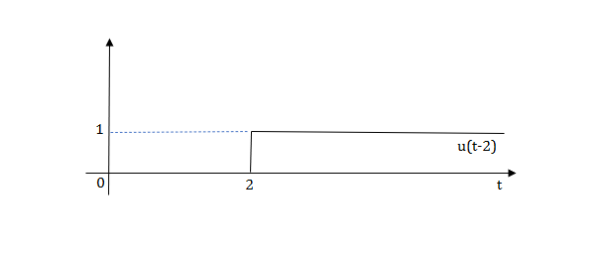

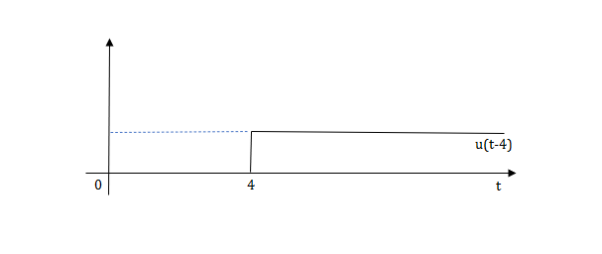

The final equation is=u(t)+u(t-1) +u(t-2) +u(t-3)-4u(t-4)
As the waveform is stopped at t=4 with amplitude 4, so we have to balance that using -4u(t-4).
Ramp function:
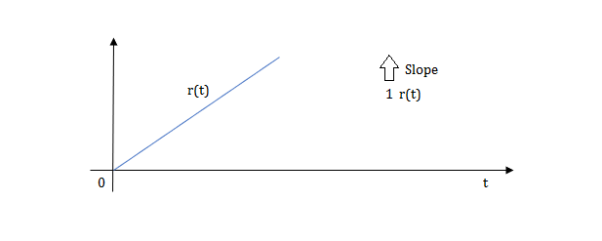

L[r(t)] =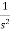
R(t)=tu(t)
R(t)=∫u(t)
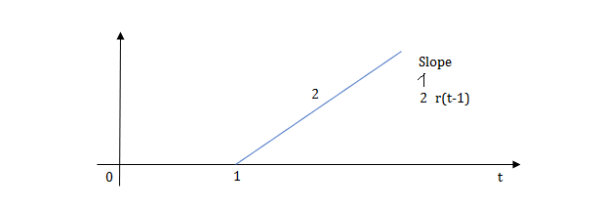
Q.3) Write the equation for the given waveform?
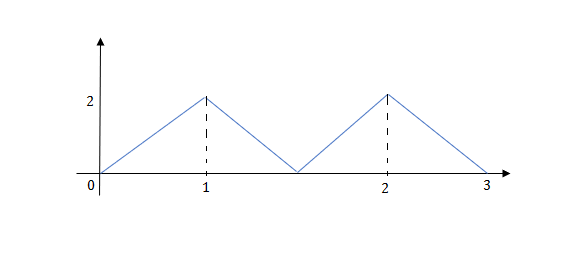
Sol: Calculating slope of above waveform
Slope for (0,0) and (1,2)
a1 slope=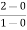 =2
=2
a2 slope=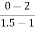 =-4
=-4
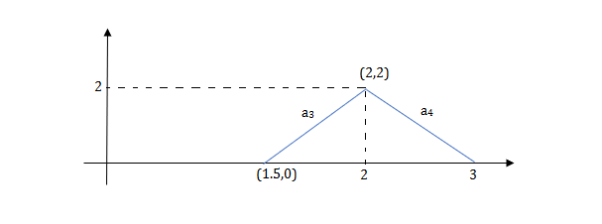
a3 slope =4 and a4= -2

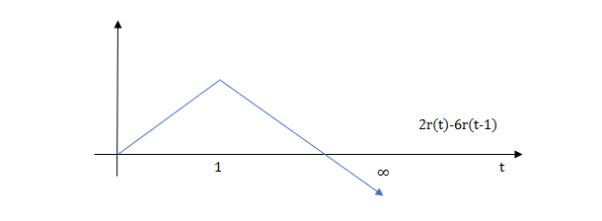
At t=1 slope change from 2 to -4 so we need to add -6r(t-1) to 2r(t) to get the slope of -4.

At t=1.5 slope changes from -4 to 4 so adding 8r(t-1.5) to get slope of 4
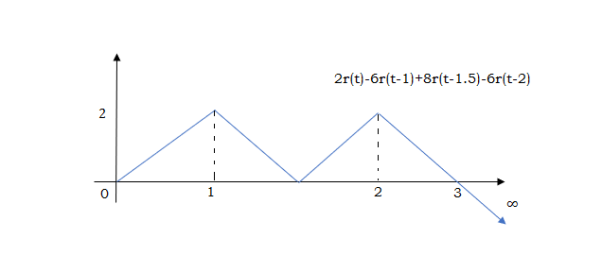
At t=2 slope changes from +4 to -2 so we add -6r(t-2). But we need to stop the waveform at t=3. Hence, we have to make slope 0. Which can be done by adding +2r(t-3). Final equation is given as
2r(t)-6r(t-1.5) +8r(t-1.5)-6r(t-2) +2r(t-3)
Their Laplace transforms, Representation of R, L, C in S domain
If LT[f(t)] = F(s)
Where F(s)=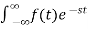 dt
dt
f(t) F(s)
F(s)
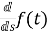
 sF(s)-f(0-)
sF(s)-f(0-)
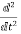 f(t)
f(t) S2F(s)-sf(0-)-f’(0-)
S2F(s)-sf(0-)-f’(0-)
Now, we find Laplace for 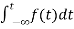
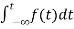 =
=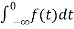 +
+
Now if f(t)=ic(t) [current through capacitor]
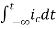 =
=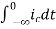 +
+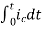
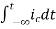 =
=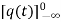 +
+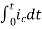
= [q (0)-q (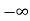 )]+
)]+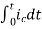
=[q(0)-0]+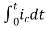
Multiplying both sides by 1/C
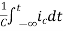 =
=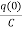 +
+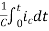
Vc(t)= +
+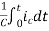
Vc(t)=Vc(0)+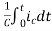
By Laplace Transform
Vc(s)= +
+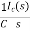
Vc(s)=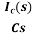 +
+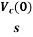

Now by source conversion
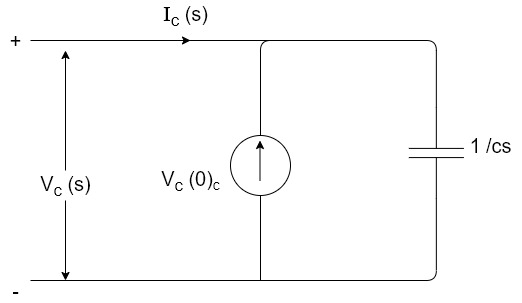
 =
= +
+
Now if f(t)=VL(t) [voltage across inductor]
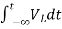 =
=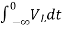 +
+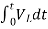
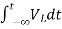 =
=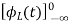 +
+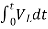
=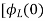 -
-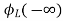 ]+
]+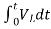
=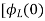 -0] +
-0] +
Multiplying both sides by 1/L

 =
=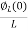 +
+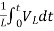
iL(t)=iL(0)+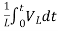
By Laplace Transform
IL(s)=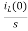 +
+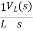
IL(s)=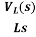 +
+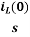
NOTE: Voltage------->Series circuit
Current------->Parallel circuit
By source transformation
Current through capacitor
iC(t)=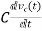
IC(s)=C[sVc(s)-Vc(0)]
Vc(s)=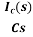 +
+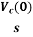
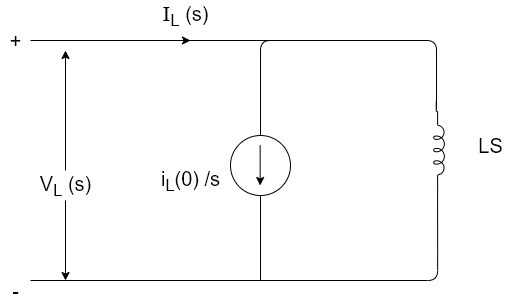
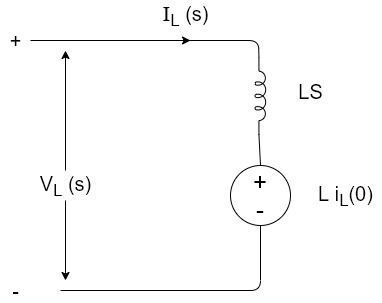
Voltage about inductor,
VL(t)=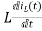
VL(s)=L[sIL(s)-iL(0)]
IL(s)=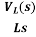 +
+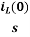

Transformed Network

Table for R,L and C and its Laplace Transform
Application of Laplace Transform:
Ques:- Find IL(0)
Diagram
Soln: - comparing with ckf,
L = 2H
LiL (0) = 25 mv
IL (0) = 12.5 m A
Que: -
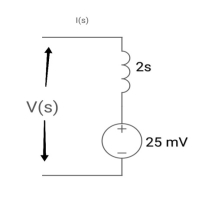
Soln: - comparing with circuit,
1/cs = 2/5
C=1/2f
Vc (0)/s = 0.25v/5
Vc (0) = .25v
Ques: -
Diagram
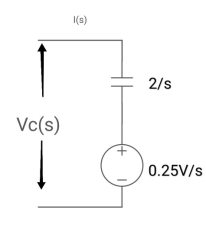
Soln: - 1/cs = 1/2S
C=2F
CVc (0) = 0.02
Vc (0) = 0.01
Que: -
Diagram
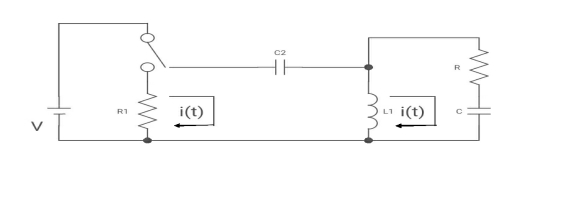
(a) switch is at before moving to position = at t= 0, at t= 0+, i1(t) is
(a) –V/2R (b) –V/R (c) – V/4R d0
Soln: -
I1(t) L.T I1(s)
I2(t) L.T I2(s)
Then express in form
[ I1(s)/I2(s)] [:]. [:]
Drawing the ckl at t = 0-
Diagram
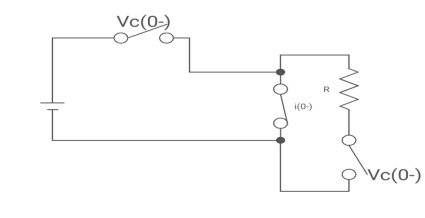
:. The capacitor is connected for long
Vc1 = v
IL (0-) = v
IL (0-) =0
Vc2(0-) =0
At t= 0+
Diagram
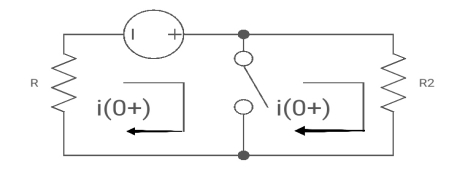

i1 (0+) = -V/2R
For t>0 he circuits ø
Diagram
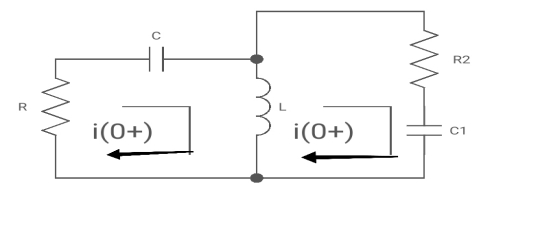
Apply KVL
-R i1(t) -1/c |i1 (t) dt – Ld./dt [i1(t) - i2 (t)]=0
Also, we can deduce i1(t)- i2 (t) = iL(t)
-RT1(t) -1/c |i1(t)-i2(t) = iL(t)
-RT1(s)- |I1(s)/cs – Vc1(0)/5] – L [ s.I1 (s) – iL (0)]
-RI1(s) –I1(s)/cs –v/s – LS Il(s) =0
-I1(s) [R +1/cs +Ls] – Ls I2(s) = -v/s -------(1)
Again,
-Ri2(t) – 1/c | i2(t) dt – d/dt [i2(t) dt – L d/dt [i2(t)- i1(t)] = 0
-R i2 (t) – 1/c |-1/c |i2(t) dt – L d/dt iL(t) = 0
Taking Laplace transform
- RI2(s) – [I2(s)/cs + vc (00/s] + L [sI1(s)- iL (0) ]= 0
-RI2(s) – I2(s)/cs +Ls [ I1cs) –I2(s)] = 0
I2 (s) [R+1/cs+Ls] – LsT1(s) = 0 --------(2)
Hence, in matrix representation,
[R+1/cs +Ls –Ls [I1(s)] [-v/s]
[-Ls R+1/cs+Ls] [I2 (s)] [0]
Ques: - diagram

All initial conditions are zero it L.T, I(s) = ?
Drawing Laplace circuit
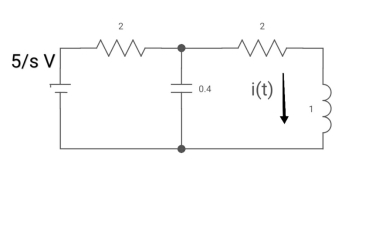
(2+S) 11 2/S
Zeq = [(2+S)2/S]/[2+S+2/S]=[2(S+2)]/[S2+2s+2]
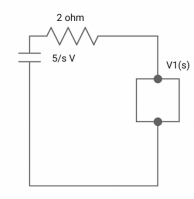
V1(s) = [5/S{2(S+2)/S2+2S+2}]/[2+{2(S+2)/ S2+2S+2}]
V1(s) = [5(S+2)/S]/[S2+ 3S +4]
I(s) = V1(s)/(S+2) = (5/S)/(S2+35+4)
Reference
- Engineering Circuit Analysis”, by W H Hayt, TMH Eighth Edition
- “Network analysis and synthesis”, by F F Kuo, John Weily and Sons, 2nd Edition.
- “Circuit Theory”, by S Salivahanan, Vikas Publishing House 1st Edition, 2014
- “Network analysis”, by M. E. Van Valkenburg, PHI, 2000
- “Networks and Systems”, by D. R. Choudhary, New Age International, 1999
- Electric Circuit”, Bell Oxford Publications, 7th Edition.