Unit 1
Introduction to Signal and System
- Signal
A signal is a description of how one parameter varies with another parameter.
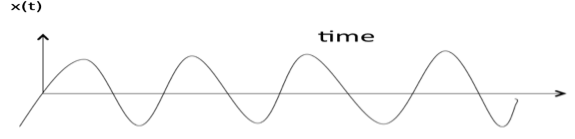
For example: voltage changing over time in an electronic circuit.
Picture brightness: A camera senses the incoming light and records the light reflectivity as a function of space onto a magnetic film.
- System
A system is a process that produces an output signal in response to an input signal.
Communication System
As illustrated in the figure system produces output signal in response to an input signal.
Also,
Continuous systems input and output continuous signals, such as analog electronics where the signal varies continuously with respect to time.
Discrete systems input and output discrete signals, such as computer programs that manipulate the values stored in arrays.
Continuous –time System and Discrete Systems
A continuous time system is one which operates on the continuous time input signal and produces a continuous-time output signal.
x(t) y(t)
If the input is x(t) and output is y(t) then
y(t) = T{x(t)}
That is x(t) is transformed to y(t).
Example: Amplifiers, filters, motors etc
Discrete time system is one which operates on discrete time input signal and produces a discrete-time output signal.
x(n) y(n)
If the input is x(n) and output y(n) then
y(n) = T[x(n)]
Static and Dynamic Systems
A system is said to be static or memoryless if its output at any instant depends on the input at that instant but not on the past or future values of input.
Otherwise the system is dynamic or with memory.
Example for static:
y(t) = x2(t)
y(n) = nx(n)
Example for dynamic
y(t) = dx(t)/dt
y(n) = x(n-1)
Find whether the following systems are dynamic or not:
a) y(t) = x(t-2)
Here, the output depends on the past value of input therefore the system is dynamic
b) y(n) = x(n+2)
The output depends on the future value of input. Therefore, system is dynamic.
c) y(t) = x2(t)
The output depends on the present input. Therefore, system is static.
Linear and Non-linear Systems.
Superposition principle states that the response to a weighted sum of input signals be equal to the weighted sum of the outputs corresponding to each of the individual input signals. A system that satisfies the superposition principle is said to be linear system.
T [a1 x1(t) + a2 x2(t)] = a1 T[x1(t)] + a2 T[x2(t)]
∴, T [a1 x1(t) + a2 x2(t)] = a1 y1(t) + a2 y2(t)
Similarly, for discrete –time linear system
T [ax1(n) + bx2(n)] = a T[x1(n) + bTx2(n)]
Example:
Check whether the systems are linear or not.
a) dy/dt + 3t y(t) = t2 x(t)
b) y(t) =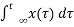 
c) y(n) = Ax(n) + B
Solution:
a) dy/dt + 3t y(t) = t2 x(t)
For input x1(t) the output is y1(t)
Dy1(t)/dt + 3t y1(t) = t2 x1(t) --------- (1)
Similarly, for x2(t) output is y2(t)
Dy2(t)/dt + 3t y2(t) = t2 x2(t) ---------- (2)
Multiply (1) with a and (2) with b
a dy1(t) /dt + 3at y1(t) + b dy2(t)/dt + 3by2(t) = at2 x1(t) + bt2 x2(t)
d/dt[ay1(t) +by2(t)] + 3t[ay1(t) + by2(t)] = t2[ax1(t) + bx2(t)]
The system is linear because weighted sum of inputs produces the corresponding weighted sum of outputs.
b) y(t) =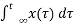 
For x1 input output is y1(t)
y1(t) =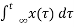
y2((t)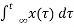 
Linear combination of both yields
ay1(t) + by2(t) = a 
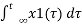+ b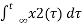 
= 
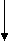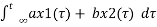
Linear combination of inputs
Linear combination of outputs
Therefore, system is linear.
c) y(n) = Ax(n) + B
For input x1(n) the corresponding output is y1(n)
y1(n) = T[x1(n)] = Ax1(n) + B; y2(n) = Tx2(n)] = A x2(n) + B
Ay1(n) + by2(n) = a[Ax1(n) + B] + b[Ax2(n) +B]
The output will be y3(n) = A[x1(n) + x2(n)] +B
y3(n) ≠ ay1(n) + by2(n)
Therefore, system is non-linear.
d) y(t) = e x(t)
y1(t) = e x1(t)
y2(t) = e x2(t)
y3(t) = T[ax1(t) + b x2(t)] = e[ax1(t)+bx2(t)]
Ay1(t) + by2(t) = a ex1(t) + b ex2(t)
y3(t) ≠ ay1(t) + b y2(t)
Hence, system is not linear.
Time Variant and Time Invariant Systems
A system is said to be time-variant if its input-output characteristics does not change with time.
Suppose we apply a signal(t) to a system to a system and obtain an output y(t) as shown in the figure.
If we delay by T seconds then for a time-invariant system the output will be delayed by T seconds.
Example
Determine whether the following systems are time variant or time invariant.
a) y(t) = x(t) cos 50πt
b) y(t) = e x(t)
c) y(t) = x(t2)
d) y(n) = x2(n-1)
a) y(t) = x(t) cos 50πt
If the input is delayed by T sec then output
y(t,T) = T[x(t-T)] = x(t-T) cos (50πt)
If the output is delayed by T sec then
y(t-T) = x(t-T) cos 50 π(t –T)
y(t,T) ≠ y(t – T)
Hence the system is time-variant.
b) y(t) = ex(t)
The output for delayed input is
y(t,T) = e x(t-T)
The delayed output is
y(t-T) = ex(t-T)
y (t, T) = y(t-T)
Hence, system is time-invariant.
c)y(t) = x(t2)
The output for delayed input is
y(t,T) = x (t2 –T)
The delayed output is
y(t-T) = x(t-T)2
y(t,T) ≠ y(t – T)
Hence the system is time variant
d)y(n) = x2 (n-1)
The output for delayed input is
y(n-k) = x2(n-1-k)
The delayed output is
y(n-k) = x2 (n-1-k)
y(n,k) = y(n-k)
System is time invariant.
Causal and Non-casual systems.
System is said to be casual if its output depends on the present and past inputs and not on the future input.
If the output depends on the future inputs then it is non- casual system.
. For example
y(t) = 2 x(t) + 3 x(t-3)
Let t=1 therefore y (1) = 2 x(1) + 3 x(-2)
The system output only depends upon present and past inputs. Hence, the system is causal.
y(t) = 2 x(t) + 3 x(t – 3) + 6 x( t+3)
Let t=1 the system output is
y(1) = 2x(1) + 3 x(-2) + 6 x( 4)
Here the output depends future input. Hence non –casual.
Problem:
a) y(n) = x(-n)
Let n=0 then y (0) = x (0)
n=1 then y(1) = x(1)
n=-1 then y(-1) = x(-1)
n =-2 then y(-2) = x(-2)
For negative value of n it output depends on the future input. Therefore system is non-casual.
c)y(t) =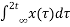 
When t=0
y(0)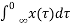 
= z(0) – z(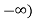
When t=1
y(1) =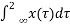 
= z(2) – z(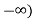
The output depends on the future value hence the system is non-casual.
Invertible and Non-Invertible systems
A system is said to invertible if the input of the system appears at the output.
Y(S) = X(S) H1(S) H2(S)
= X(S) H1(S) · 1(H1(S))/ (H1(S))
Since H2(S) = 1/( H1(S) )
∴, Y(S) = X(S)
→ y(t) = x(t)
Hence, the system is invertible.
If y(t) ≠ x(t), then the system is said to be non-invertible.
To test whether the system is invertible or not:
- If the system produces zero output for any input the system is non-invertible.
- If the system gives same output for different inputs the system is non-invertible.
Problem:
Determine if the following systems are invertible or not.
a) y(t) = cos[x(t)]
For input signals separated by 2 π the system gives the gives the same output . Hence system is non-invertible.
b) y(t) = x(t-3)
Invertible: The inverse system is x(t+3)
c) y(t) = dx(t)/dt
If x(t) is constant then the output is zero. Therefore, system is non-invertible.
d) y(n) = x(n)x(n-2)
For input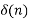 
and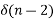 
the output is zero. Hence the system is non-invertible.
Stable and Unstable Systems
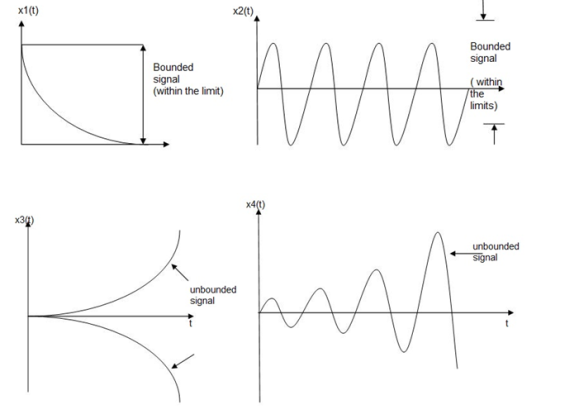
An input signal x(t) is said to be bounded if it satisfies the condition |x(t) |≤Mx < ∞ for all t.
Similarly the output signal is bounded if it satisfies the condition |y(t)| ≤My < ∞
The example for bounded and unbounded signals is as shown in the figure.
Note: For a bounded signal, amplitude is finite.
Example 1: y (t) = x2(t)
Let the input is u(t) that is unit step then output y(t) = u2(t) = u(t) = bounded output.
Hence, the system is stable.
Example 2: y (t) = ∫x(t)dt∫x(t)dt
Let the input be u (t) then
Output y(t) = ∫u(t)dt but ∫ u(t)dt = ramp signal
It is unbounded because the amplitude of ramp is not finite and tends to become infinite when t →infinite
Hence, the system is unstable.
Problems:
Check whether the following systems are
Static or dynamic
Linear or Non-linear
Causal or non-casual
Time Invariant or time variant
a) y(t) d2y(t) /dt2 + 3t dy(t)/dt + y(t) = x(t)
- Since it is a differential equation the system is dynamic.
- The input x1(t) and output y1(t) can be described by
y1(t) d2 y1(t)/dt2 + 3t dy1(t)/dt + y1(t) = x1(t)
Similarly, y2(t) d2y2(t)/dt2 + 3t dy2(t)/dt + y2(t) =x2(t)
a y1(t) d2y1(t)/dt2 + 3at dy1(t)/dt + a y1(t) + b y2(t) d2y1(t)/dt2 + 3bt dy1(t)/dt +by2(t) = ax1(t) + b x2(t)
Ay1 d2 y1(t)/dt2 + by2(t) d2 y(t)/dt2 + 3t d/dt[ay1(t) + b2 y2(t)] + ay1(t) + b y2(t) = ax1(t) + bx2(t)
Since the differentiation ay1(t) d2 y1(t)/dt2 + by2(t) d2 y2(t)/dt2 is not a function of the weighted sum of outputs, superposition principle is not satisfied hence the system is non-linear.
- The output depends on the present input only hence the system is causal.
- The co-efficient of the differential equations are function of time. Hence the system is time-variant.
y(n) = x(n) x(n-1)
The output depends the past values of input. Hence it requires memory therefore the system is dynamic.
The output y1(n) for input x1(n) is
y1(n) = x1(n) x1(n-1)
y2(n) = x2(n) x2(n-1)
y3(n) = ax1(n) + b x2(n) [ax1(n-1) + b x2(n-1)]
a y1(n) + by2(n) = a x1(n) x1(n-1) + bx2(n) x2(n-1)
Since y3(n) ≠ ay1(n) + b y2(n)
Hence the system is non-linear.
The output depends on the present and past values of input. Hence the system is casual.
y(n) = x(n) x(n-1)
y (n, k) = x(n-k) x(n-1-k)
y(n-k) = x(n-k) x(n-1-k)
Since y(n,k) = y(n-k) the system is time-invariant.
b) y (n) = cos[x(n)]
The output depends on the input at that instant. Therefore, system is static.
For input x1(n)
y1(n) = cos[x1(n)]
For input x2(n)
y2(n) = cos[x2(n)]
y3(n) = cos[ax1(n)+ b x2(n)]
a y1(n) + b y2(n) = a cos [x1(n)] + b cos[x2(n)]
Hence the system is non-linear.
The output depends on the present input hence the system is casual.
y(n) = cos[x(n)]
y(n,k) = cos[x(n-k)]
y(n-k) = cos[x(n-k)]
y(n,k) = y(n-k)
Hence system is time –invariant.
For the given system check whether the system is linear, time-invariant ,casual memoryless or stable.
Y(t) = x(t-2) + x(2-t)
- System is not memoryless since the output depends on the past and future values of input.
- The system is non-casual since output depends on the future values of input.
y (t,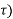
= x1(t-2-
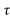)+x1(2-t-
)
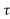y(t-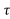
) = x(t-2-
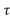) + x2(2-t+
)
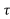y (t,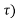
≠ y (t-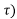
System is time variant.
y1(t) = x1(t-2) + x1(2-t)
y2(t) = x2(t-2) + x2(2-t)
a1y1(t) + a2 y2(t) = a1 x1(t-2)+ a1x1(2-t) + a2x2(t-2)+a2x2(2-t)
= a1x1(t-2) + ax2(t-2) +a1x1(2-t)+a2 x2(2-t)
= System is linear.
For bounded input, the output is also bounded. Hence the system is stable.
We need to obtain the response of the signal for a specific input. But the question is, the input can be varying signal or sometimes random signal. Therefore, some standard test signals are required to know the performance of the system. Thus, the standard input signals include:
- An impulse
- Step
- Ramp
- Parabolic input.
Impulse Signal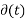 
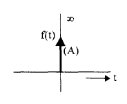
The impulse response is as shown in the figure.
- The impulse response is zero for t ≠ 0.
- It rises to infinity at t = 0– and comes back to zero at t = 0+ enclosing a finite area.
- If this area is A it is called as an impulse function of strength A.
- If A = 1 it is called a unit impulse function.
Thus, an impulse signal is denoted by f(t) = A (t).
Properties on Impulse function:
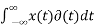= x (0)
=x(t0)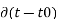 
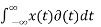= x(t0)
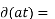1/|a| 
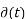
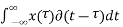=x(t)
Evaluate the following integrals:
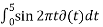
(t-3) 2 dt
Solution:
1) 
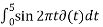
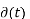= 1 for t=0. For t≠ 0 =0.
= 
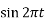|t=0 = 0
2) 
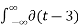(t-3) 2 dt for t=3 
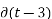= 1
(t-3) 2 |t=3 =0
Step Signal
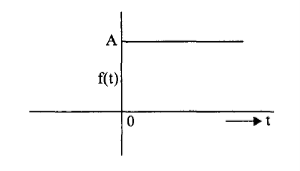
The step signal is as shown in the figure.
- For t<0 it is zero.
- For t=0 it rises to A
- For t>0 it remains the same.
Thus, the step signal is denoted by f(t) = A u(t). If A=1 it is called unit step function.
Ramp Signal
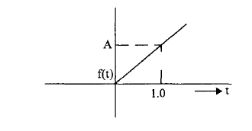
The ramp signal is as shown in the figure.
- For t<0 it is zero.
- Uniformly increases with slope = A.
It is denoted by f(t) = At. If the slope is unity then it is called a ramp signal.
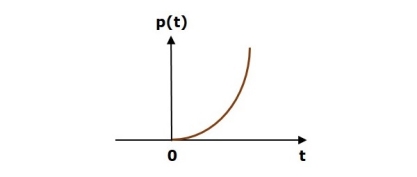
Unit Parabolic Signal
A unit parabolic signal, p(t) is defined as,
p(t) = t2/2; t≥0
=0; t<0 and t=0
We can write unit parabolic signal p(t) in terms of unit step signal u(t) as
P(t) = t2/2 u(t).
The following figure shows the unit parabolic signal.
- Periodicity
The signal’s behaviour/graph repeats after every T. Therefore,
x(t) = x(t + nT) or
x(t) = x (t – nT)
Where, T is the fundamental period. So, we can say that the signal remains unchanged when shifted by multiples of T.
Find the fundamental period T of the following continuous time signals
- Sin 50 π t
x(t) = sin 50 π t where Ωo = 50 π.
Time period T = 2 π/ Ωo = 2 π/50 π = 1/25. Sec
2. x(t) = 20 cos (10 πt + π/6) Ωo = 10 π
T = 2π/ Ωo = 2π/10 π = 1/5 sec.
Check whether the following signals are periodic or not
x(t) = 2 cos (10t+1) – sin(4t-1)
Time period 2 cos (10t+1) is T1 = 2 π/10 = π/5
Sin(4t-1) T2 = 2π/4 = π/2
T1/T2 = π/5/ π/2 = 2/5.
Since it is rational number the signal is periodic with period T = 2T2 =5 T1
= π sec.
x(t) = sin2t
= 1-cos2t
2
Period of the signal is T = 2 π/ Ω0 = 2 π/ 2= π
Signal is periodic.
x(t) = ej2 π/3n + ej 3 π/4n
Time period for ej2 π/3n
N1 = (2 π/ (2 π/3)) = 3m Here m=1 N1=3
Time period for ej 3 π/4n
N2 = (2 π/ (3 π/4)) = 8/3m here m=3 N2=8
N1/N2 = 3/8
8 N1 = 3 N2
N = 8N1=3N2 = 24.
N=24.
- Even and Odd
An even signal is symmetric about the Y-axis.
x(t) = x(-t) even
x(t) = - x(-t) odd
The signal can be broken into even and odd parts by
x(t) = x (t + nT)
x(t) = x (t – nT)
Find the even and odd of the signal as shown in the figure
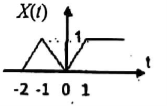
Step 1: Find the signal x(-t)
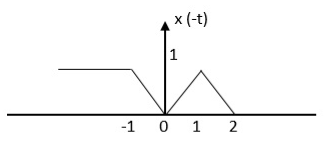
The even signal is xe(t) = x(t) +x(-t)
Therefore
Xe(t) = ½ x(t) +x(-t)/2
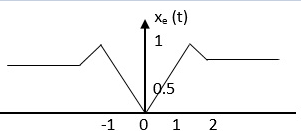
For odd the signal is
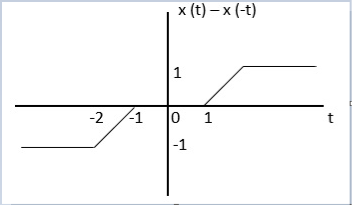
Xo(t)
- Time Invariant
Any delay provided in the input must be reflected in output for time invariant system
Take x2(t) = x(t –T)
Then y(x2(t)) must be x2(y(t))
Here x2(t) is a delayed input.
We see that if there is a delayed input through the system is the same delay is in the output signal.
y(t) = e x(t)
y(t) = ex(t-T)
y(t-T) = ex(t-T)
y(t) = y(t-T)
System is in-variant.
Properties of Linear System
There are the properties
Homogeneity
Additivity
Homogeneity
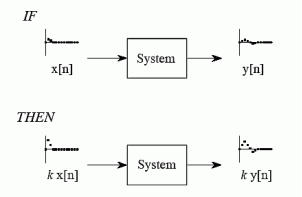
Homogeneity means change in input signals amplitude results in a corresponding change in the output signal’s amplitude.
That is a change in x[n] will result in a change in y [n]
Also, a change in k x[n] will result in a change in k y[n]
Additivity
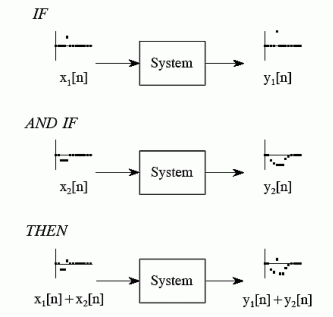
Consider a system where input x1[n] produces an output y1[n]. Similarly, x2[n] produces y2[n].
The system is additive when
x1[n] + x2[n] = y1[n] + y2[n]
In other words, signals added at the input will produce signals added at the output.
- BIBO stability
Bounded input bounded output stability.
The system is BIBO stable if
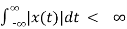
- Causality
Causal signals are signals that are zero for all negative time. If any value of the output signal depends on a future value of the input signal then the signal is non-causal.
Example
Y(t) = ½[x(t) – x(-t)]
For negative values of t the output depends on future values of input
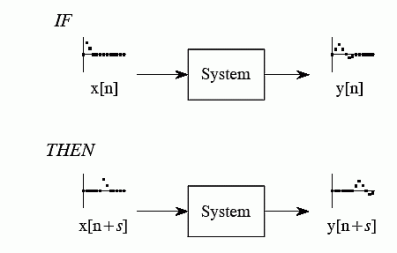
Shift Invariance
Shift invariance means that a shift in the input signal will result in an identical shift in the output signal
If x[n] -> y[n]
Then x[n+s] -> y[n +s] for any constant s
Check whether the following systems are casual or not.
y(n) = x(n) + 1/x(n-1)
For n=0
y(0) = x(0) + 1/x(0 -1)
For n=1
y(1) = x(1) + 1/ x(0)
For n=2
y(2) = y(2) + 1/x(1)
For n=-1
y(-1) = x(-1) + 1/x(-2)
For all values of n the output depends on the present and past values of input. Hence the system is casual.
References:
Signals and Systems by Simon Haykin
Signals and Systems by Ganesh Rao
Signals and Systems by P. Ramesh Babu
Signals and systems by Chitode
