Unit 2
Linear time-invariant Systems
A linear time-invariant system is represented by its impulse response. If X(t) is the input signal to the system, then output is represented as
Y(t) = 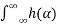 X(t-
X(t-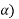 d
d 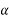 =
=  h(t-
h(t-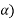 d
d 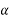 ---------------(1)
---------------(1)
The above integral is called convolution of h and X where
Y(t) = h(t) * X(t) = X(t) * h(t) -----------------------------(2)
The impulse response can be obtained is the input is unit impulse function. For discrete-time systems the output is written as
Y(n) = h(n) * X(n) = X(n) * h(n) = 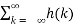 X (n-k) = =
X (n-k) = = 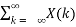 h(n-k)--------(3)
h(n-k)--------(3)

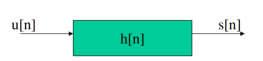
The step response of a discrete-time LTI system is the convolution of the unit step with the impulse response-
s[n]=u[n]*h[n]. -------------------(1)
Commutative property of convolution,
s[n]=h[n]*u[n]. ----------------------------------------(2)
That means s[n] is the response to the input h[n] of a discrete-time LTI system with unit impulse response u[n].

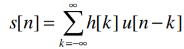 -------------------------(1)
-------------------------(1)
Since u [n- k]< 0 is for n- k< 0, i.e. k> n and 1 for n -k> 0, i.e. k≤ n.
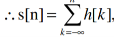 ----------------------------------------(2)
----------------------------------------(2)
That is the step response of the discrete LTI system is the running sum of its impulse response.

From here h[n] can be recovered from s[n], the impulse response of discrete-time LTI system is the first difference of its step response.
For continuous time system
The unit step response is the running integral of its impulse response.
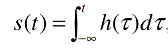
The unit impulse response is the first derivative of the unit step response: -
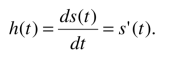
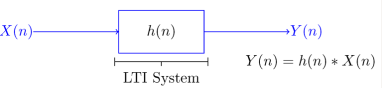
The input signal to the system is x(n) and the output is y(n).


 x(n) y(n) = T[x(n)]
x(n) y(n) = T[x(n)]
If the input to the system is unit impulse then the output of the system is known as impulse response of the system denoted by h(n).
h(n) = T [ ∂(n)]
The arbitrary sequence x(n) can be represented aa a weighted sum of discrete impulses given by
x(n) = 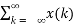 ∂(n-k)
∂(n-k)
Then the output
y(n) = T [ 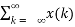 ∂(n-k)]
∂(n-k)]
Using linear property of the system, interchange the system operator T with the summation x(k) to obtain
y(n) = 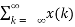 T [ ∂(n-k)]
T [ ∂(n-k)]
Now
y(n) =  h(n,k)
h(n,k)
For a time-invariant system
h(n,k) = h(n-k)
Therefore
y(n) =  h(n-k)
h(n-k)
Thus, the output of the LTI system is given by the weighted sum of the time-shifted responses.
This sum is termed as convolution sum represented as
y(n) = x(n) * h(n) where * denotes convolution.
Problem:
The impulse response h[n] of a discrete-time LTI system. Determine and sketch the output y[n] of this system to the input x[n]
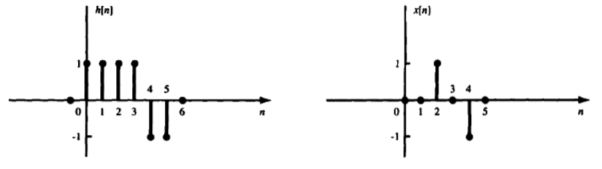

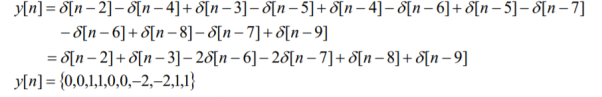

Stability:
A system is said to be stable if a bounded input sequence produces bounded output sequence. For bounded input sequence x(n) if the output is unbounded the system is said to be unstable system.
Let x(n) be a bounded input sequence satisfying |x(n) | ≤ Mx < ∞. Let h(n) be the impulse response of the system then the output y(n) can be found by convolution sum . That is
y(n) = 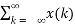 h(n-k) = =
h(n-k) = =  x(n-k)----------------------(1)
x(n-k)----------------------(1)
The magnitude of the output is given by
|y(n)| = | 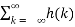 x(n-k)|-------------------------(2)
x(n-k)|-------------------------(2)
We know that the magnitude of the sum of terms is less than or equal to the sum of the magnitudes, hence
|y(n)| = | 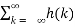 x(n-k)|≤
x(n-k)|≤ 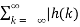 || x(n-k)| --------------------(3)
|| x(n-k)| --------------------(3)
Let the bounded value of the input be equal to M then eq(3) can be written as
|y(n) | ≤ M 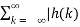 |------------------------------(4)
|------------------------------(4)
The above condition is satisfied when
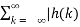 | < ∞ ------------------------(5)
| < ∞ ------------------------(5)
Therefore, the necessary and sufficient condition for stability is
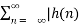 | < ∞ -----------------------(6)
| < ∞ -----------------------(6)
Therefore, the LTI system is stable if its impulse response is absolutely summable.
Causality:
If x(t) = ∂(t) then according to convolution theorem
y(t) = x(t) * h(t) = h(t) * ∂(t) = h(t)
A casual system is one where the output at the present instant does not anticipate input from future instants.
X(t) , t<to ------- y(t) , t<to
An LTI system is casual if and only if
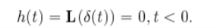
The impulse response of the system has to be zero for negative time for the system to be casual.
For discrete time system the impulse response of the sequence h[n] of LTI system has to be right -sided sequence
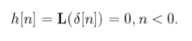
For the given impulse response h(n) of the system determine if the system are casual or stable.
h(n) = 2 n u(-n)
The given system is non casual since h(n) ≠0 for n<0. For stability the impulse response must be absolutely summable.
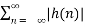 < ∞
< ∞
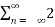 n u(-n) =
n u(-n) =  n =
n = 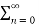 (1/2) n = 1+1/2 +………………. = 1/ 1-1/2 = 2
(1/2) n = 1+1/2 +………………. = 1/ 1-1/2 = 2
Hence system is stable.
An LTI system is specified by equation
d 2 y(t)/ dt 2 + 5 d y(t) /dt + 6 y(t) = dx(t) / dt + 4 x(t)
The input is x(t) = e -t u(t)
Find the natural response for initial conditions:
y (0+) = 3 d y(0+)/dt =0
Forced response
Total response.
Given d 2 y(t) / dt 2 + 5 d y(t)/dt + 6 y(t) = d x(t)/dt + 4 x(t)
The natural response can be obtained by equating input terms in differential equation to zero.
d 2 y(t) / dt 2 + 5 d y(t)/dt + 6 y(t)=0
The characteristic equation is
- 2 + 5
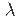 + 6=0
+ 6=0
- 1=-2 and
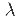 2 = -3
2 = -3
The homogenous solution is
Yh(t) = c1 e -2t + c2 e -3t
y (0+) = c1 + c2
d y (0+)/dt = 2 c1 e -2t + (-3) c2 e -3t |t=0
= 2c1 – 3c2
From initial conditions
y (0+) = 3
Dy (0+)/dt =0
Comparing we get c1 + c2 =3
2c1 + 3c2 =0.
c2 =-6 and c1=9
Yn(t) = 9 e -2t – 6 e -3t
Forced response:
The homogeneous solution is given by
Yn(t) = c1 e -2t + c2 e -3t
For input x(t) = e -t
The particular solution is of the form
Yp(t) = k e -t
From which
Dyp(t)/dt = -k e-t
d2 yp(t)/dt2 = k e-t
Therefore,
d 2 yp(t)/dt2 + 5 d yp(t)/dt + 6 yp(t) = dx(t)/dt + 4 x(t)
k e -t – 5 k e-t + 6 k e-t = - e-t + 4 e-t
2k = 3
K=1.5
Yp(t) = 1.5 e -t.
The forced response is the sum of homogeneous solution for particular solution.
Yf(t) = c1 e -2t + c2 e -3t + 1.5 e -t
y(0+) = c1 + c2 +1.5
Dy(0+)/dt = -2c1 e -2t -3 c2 e -3t – 1.5 e -t |t=0
To obtain forced response equate initial conditions to zero
C1 + C2 = -1.5
2C1 + 3C2 = -1.5
Solving for c1 and c2 we get
C2 = 1.5
C1 =-3
y(t) = yn(t) + yf(t)
Substituting yn(t) and yf(t) we get
y(t) = 6 e -2t – 4.5 e -3t + 1.5 e -t
y(0) = c1 + c2 + 1.5 =3
Dy(0+)/dt = -2c1 -3c2 -1.5 =0
c1 =6 and c2 =-4.5
y(t) = 6 e -2t -4.5 e -3t + 1.5 e -t
Problem:
Consider the difference equation given by
y[n] + 0.5 y[n-1] = (-0.8) n u[n]
The solution is composed of natural response and forced response of the system.
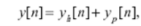
Where the particular solution satisfies for n≥0 and the homogeneous solution satisfies
Yh[n] + 0.5 yh[n-1] = 0
For n ≥0 yp(n) = y (-0.8) n
Then we get
Y (-0.8) n + 0.5Y(-0.8) n-1 = (-0.8) n
Y [ 1+0.5(-0.8) -1] = 1
Y=8/3
Which yields yp(n) = 8/3 (-0.8) n
To determine yh(n)

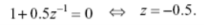

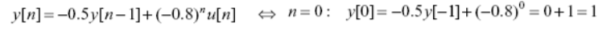
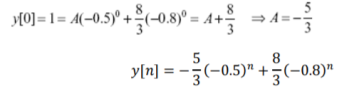
References:
Signals and Systems by Simon Haykin
Signals and Systems by Ganesh Rao
Signals and Systems by P. Ramesh Babu
Signals and Systems by Chitode