Unit 3
Laplace Transformation
Consider an LTI system by a complex exponential signal of the form
x(t) = Gest.
Where s = any complex number = σ+jω
σ = real of s, and
ω = imaginary of s
The response of LTI can be obtained by the convolution of input with its impulse response i.e.
y(t)=x(t)×h(t)=
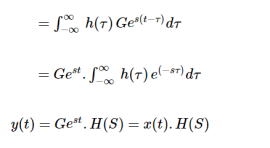
Where H(S) = Laplace transform of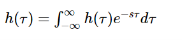 
Similarly, Laplace transform of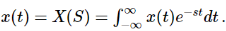 
Example :
Find the Laplace transform of e –t .
F(s) = 
F(s) =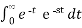 
F(s) =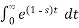 
F(s) = 1 / 1-s [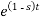
]0 
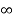
F(s = 1/ s-1.
Find the Laplace transform of unit -step function.
f(t) = 1 (t≥0)
F(s) = 
-st dt = -1/s e -st | 0 ∞ = 1/s [ e -∞ - e -0] = 1
F(s) = 1/s.
Find the Laplace transform of
f(t) = cos wt
f(t) = (1/2) e jwt + (1/2) e – jwt
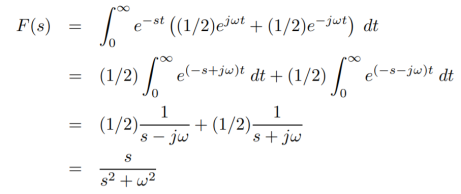
Find the Laplace transform of :
f(t) = t n ( n ≥ 1)
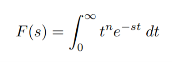
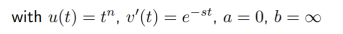
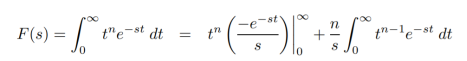
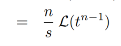
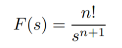
Impulse function
f(t) =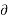 
The important functions are:
- Linearity
If there are two signals f and g and a is scalar then
L(af) = a F.
L(f + g) = F + G
That is homogeneity and superposition holds good.
Example :
Find the Laplace transform of L (
) .
F(s) =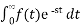 
= 3 L((
- 
))
= 3 – 2/s-1 [ e-t = 1/s-1]
= 3s-5/s-1.
Time Scaling
Definition:
If g(t ) = f(at) then where a>0 then
G(s) = 1/a F(s/a)
Here the time is scaled by a therefore frequency by 1/a
G(s) =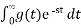 
G(s) = 
G(s) =
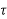
G(s) = 1/a F(s/a)
L(e at) = 1/a(1/(s/a) – 1)
L (e at ) = 1/s-a.
Exponential Scaling
Definition:
Let f be a signal and a be scalar then
g(t) = e at f(t) then
G(s) = F(s-a) .
G(s) =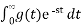 
G(s) =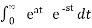 
G(s) =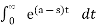 
G(s) =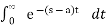 
= F(s-a)
Example
Find the L(cos t) = s/ s2 + 1
Therefore L( e-t cos t) = s+1/ (s+1)2 + 1
Derivative
If the signal f is continuous at t=0 then
L(f) = s F(s) – f(0).
- Time-domain differentiation becomes multiplication by frequency variable s
- The initial condition is –f(0).
For higher order derivatives apply the formula twice that is
L(f’’) = s L(f’) – f’(0)
= s (sF(s) – f(0)) – f’(0)
= s2 F(s) – s f(0) – f’(0)
Example :
Find the derivative of et
L(f) = 1/s-1
L’(f) = s(1/s-1) – 1
= s/s-1 – 1
= 1/s-1.
Find the derivative of sinwt.
L(sin wt) =- 1/w d/dt coswt
L(sin wt) = -1/w ( s s/s2 + w2 - 1 )
= w / s2 + w2
Integral
Let g be the running integral of signal f
g(t)=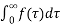 
then
G(s) = 1/s F(s)
That is the time-domain integral becomes division by frequency variable s.
Example :
Find the Laplace function of f=δ that is F(s) =1
Here g is the unit step function Therefore G(s) = 1/s.
For ramp function
g(t) = t for t≥0
G(s) =1/s2
First shifting theorem:
This theorem states that
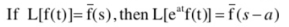
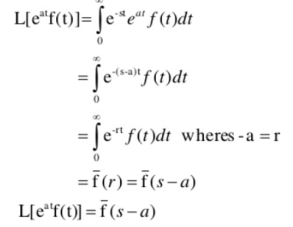
Similarly,
Find the Laplace transform of :
L ( e -3t cos 4t)
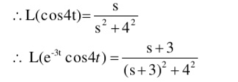
Find the Laplace transform of :
L ( e 2t cosh 2t)
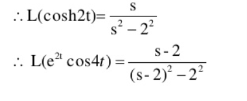
Second Shift Theorem
If L{f(t)} = F(s) and g(t) = {f(t-a) t>a }
0 t<a
Then L{g(t)} = e-as F(s)
Proof:
g(t) = f(t-a) t>0
0 t<0
Proof:
L{g(t)} =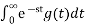 
= 
+ 
= 
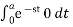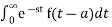
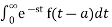
Let z =t-a or t = z+a ; dt = dz.
When t=a z =0;
t = ∞ z = ∞ ;
Therefore,
L { g(t) }= 
L{g(t)}=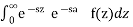 
= 
= 
L { f(z)}
L{ g(t) } = 
L { f( t-a)}
= 
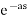F(s)
Second shifting theorem
L { f(t) } =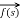 
then
L { f(t-a) u(t-a) } = e -as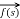 
Proof :
By definition of Laplace transform we have
L{f(t-a) u(t-a) } = 
-st f(t-a) u(t-a) dt
= 
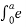-st f(u-a) (0) dt + 
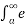-st f(t-a) (1) dt
= 
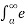-st f(u-a) dt Substituting t-a = r
= 
-s(a+r) f(r) dr
= e -as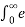 
-sr f(r) dr = e -as f (s)
L{f(t-a) u(t-a)} = e -as 
L [f(t)]
L -1 { e -at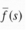 
] = f(t-a) u(t-a)
Problem:
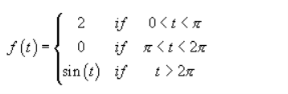
Can be written as
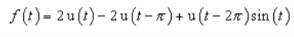
The Laplace transform can be written as
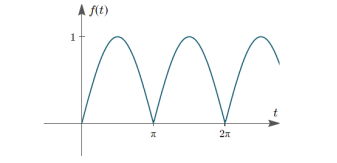
If function f(t) is periodic with p>0 so that f(t+p) = f(t) and f1(t) is one period of the function.
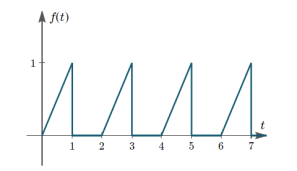
Find the Laplace transforms of the periodic functions shown below:
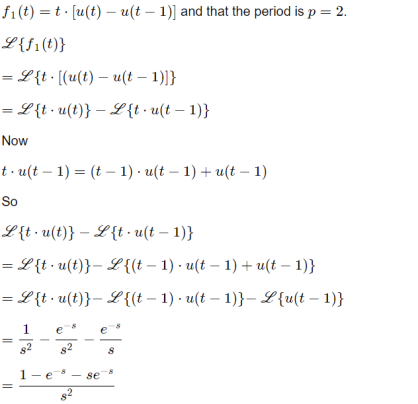
Hence, the Laplace transform of the periodic function, f(t) is given by:
Saw tooth waveform
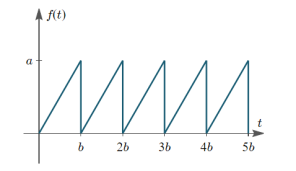
We can see from the graph that
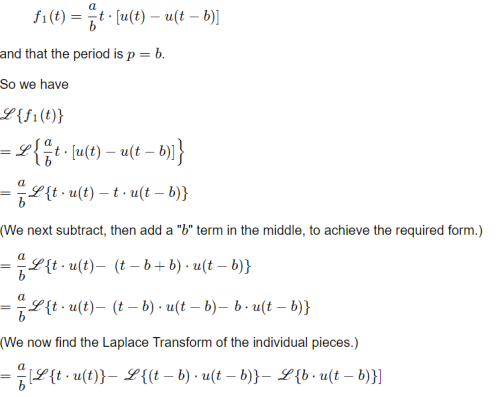
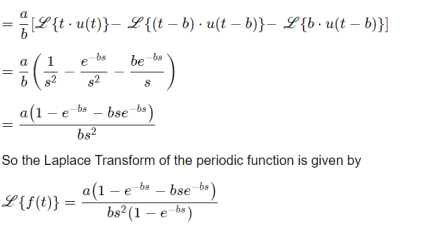
Full-wave rectification of sin t
The impulse response of linear system hr(t) is the output of the system at time t and impulse time 
. This can be written as
h r = H(∂r) ----------------(1)
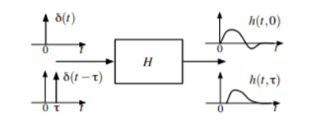
When hτ (t) = H(δτ (t)) the variable t serves different roles on each side of the equation. t on the left is a specific value for time, the time at which the output is being sampled. t on the right is varying over all real numbers, it is not the same t as on the left.
The output at time specific time t on the left in general depends on the input at all times t on the right (the entire input waveform).
Assume the input impulse is at τ = 0, h = h0 = H(δ0). To know the impulse at time t = 2. δ (2) is something like zero, so H(0) would be zero. This is not the case but h(2) depends on the entire waveform not just the value at t=2.
Output of an LTI system
To derive an expression for output y(t) of an LTI for given input x(t)
The signal x(t) as a sample
x(t) =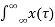 
T (t) d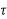
--------------------(1)
This means that x(t) can be written a weighted integral of ∂ functions.
Applying the system H to the input x(t)
y (t ) = H (x(t))
= H 
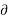T (t) d
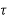---------------(2)
If the system obeys extended linearity, we can interchange the order of the system operator and the integration
y(t) = 
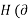T (t)) d
The impulse response is
Hr(t) = H (∂ r(t)) -----------------------------(3)
Substituting for the impulse response gives
y(t) =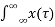 
h T (t) d
This is called superposition integral. The values x(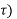
h(t,
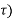d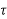 
are superimposed for each input time 
.
If H is time invariant this is written as
y(t) = 
h T (t) d 
This is convolutional integral.
Graphically this can be represented as :
System Equation:
The system equation relates the output of a system to its inputs.
The system is described by
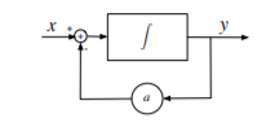
Has system equation y’ + ay = x. In addition the initial conditions must be given to uniquely specify the solution.
Solving the system equation tells us the output for a given input . The output consists of two components :
The zero-input response – which is what the system does with no input at all. This is due to intial conditions such as energy stored in capacitors and inductors.
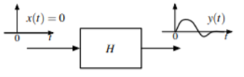
The zero state response which is the output of the system with all initial conditions zero.
If H is a linear system is zero-input response is zero. Homogenity states if y=F(ax) then y=a F(x). If a=0 then a zero input requires zero output.
Solve for the voltage across the capacitor y(t) for an arbitrary input voltage x(t) given an initial value y(0) = Yo
x(t) = R i(t) + y(t)
Using i(t) = C y’(t)
R = C y’(t) + y(t) = x(t)
To solve for homogeneous solution set the RHS to zero
C y’(t) + y(t) =0
The solution is
y(t) = A e -t/RC which can be verified by direct substitution.
To solve for total response, we let the undetermined co-efficient be function of time
y(t) = A(t) e -t/RC
Substituting this in differential equation is
RC [ A’(t) e-t/RC – 1/RC A(t) e – t/RC ] + A(t) e-t/RC = x(t)
Simplifying
A’(t) = x(t) [1/RC e t/RC] which can be integrated from t=0 to get
A(t) = 
[ 1/RC e τ/RC ] dτ + A(0)
Initial value theorem and Final value theorem are together called as Limiting Theorems.
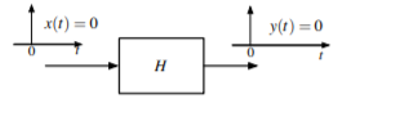
Conditions for the existence of Initial value theorem
- The function f(t) and its derivative f(t) should be Laplace transformable.
- If time t approaches to (0+) then the function f(t) should exists.
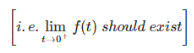
The function f(t) = 0 for t > 0 and contains no impulses or higher order singularities at origin.
If f(t) and F(s) is Laplace transform pairs. That is 
then Initial value theorem is given by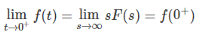
Proof
Laplace transform of a function f(t) is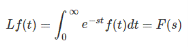
then Laplace transform of its derivative f ‘ (t) is
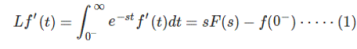
Consider the integral part first
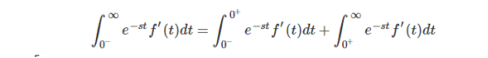
[lim s->∞ e -st is indeterminate and hence splitted into two integrals
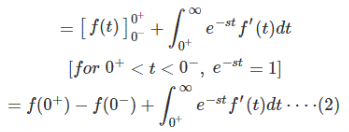
Substituting (2) in (1) we get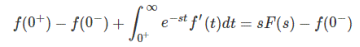
Upon cancelling f (0–) on both sides we get
On considering (s) tends to infinity on both sides in (3)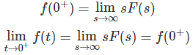
Hence, Initial value theorem is proved.
Example 1 :
Find the initial value for the function f (t) = 2 u (t) + 3 cost u (t)
Sol:
f(t) = 2 u(t) + 3 cos(t) u(t) then
F(s) = 2/s + 3s/ s 2 + 1
s F(s) = 2 + 3 s 2 / s 2 + 1
By initial value theorem
Lim t -> 0+ f(t) = lim s-> ∞ s F(s) = f(0+)
Here lim s-> ∞ s F(s) = lim s-> ∞ [ 2 + 3 / 1 + 1/ s 2 ] = 5 = f(0+)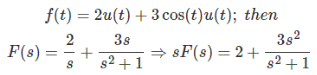 
The initial value is given by 5.
Example 2:
Find initial value of the transformed function
Sol:
By initial value theorem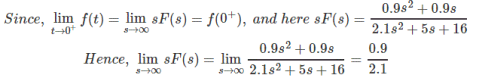
[as s → ∞ the values of s become more and more insignificant hence the result is obtained by simply taking the ratio of leading co-efficient]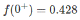
Example 3:
Find the initial value of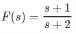 
Solution:
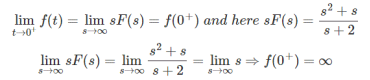
Final value theorem
If f(t) and f'(t) both are Laplace Transformable, and sF(s) has no pole in jw axis and in the R.H.P. (Right half Plane) then,
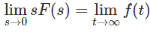
Proof
We know differentiation property of Laplace Transformation: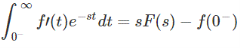
Now we take limit as s → 0. Then e-st → 1 and the whole equation looks like
If sF(s) has poles on the right side of s plane.
If sF(s) has conjugate poles on jw axis.
If sF(s) has pole on origin.
Then apply
Find the final values of the given F(s) without calculating explicitly f(t)
Answer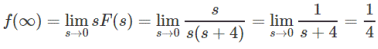
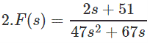
Answer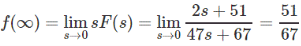
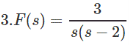
Answer
In Example 1 and 2 we have checked the conditions too but it satisfies them all. So we refrain ourselves of showing explicitly. But here the sF(s) has a pole on the R.H.P as the denominator have a positive root.
So, here we can’t apply Final Value Theorem.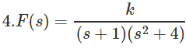
Answer
In this example sF(s) has poles on jw axis. +2i and -2i specifically.
So, here we can’t apply Final Value Theorem as well.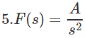
Answer
In this example sF(s) has pole on the origin.
So here we can’t apply Final Value Theorem as well.
Laplace transform in circuit analysis
Time domain S- domain
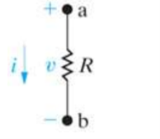
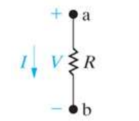
v(t) = R i(t) V(s) = R I(s)
Laplace transforms of inductors
Time domain S domain
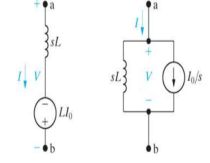
V(t) = L di/dt V(s) = s L I(s) – L Io
i(0) = Io I(s) = V(s) / sL + Io / s
Laplace transforms of capacitance
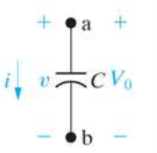
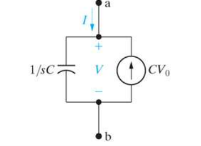
i(t) = C dv/dt I(s) = s CV(s) – C Vo
v(0) = Vo
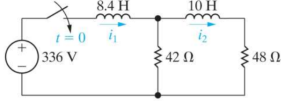
Problem:
For the circuit given find i1 and i2.
Electrical & Elect
For t> 0
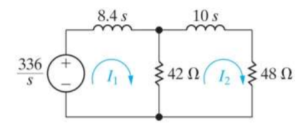
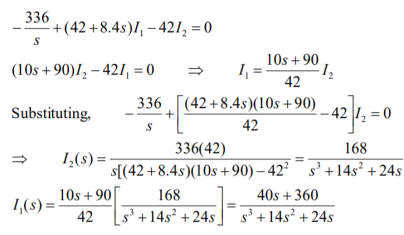
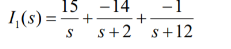
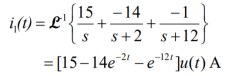
The forced response is 15 u(t) A
The natural response is [-14 e -2t – e -12t ] u(t) A
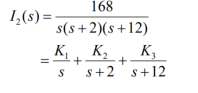
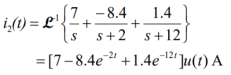
The forced response is 7 u(t) A;
The natural response is [ -8.4 e -2t – 1.4 e -12t ] u(t) A
Properties of ROC:
Property 1:
The ROC of X(s) consists of strips parallel to the jΩ – axis in the s-plane.
Property 2.
ROC does not contain any poles.
Property 3.
If x(t) is of finite duration and is absolutely integral then ROC is the entire s-plane.
Property 4:
If x(t) is a right sided signal that x(t) = 0 for t<to <∞ then ROC is of the form Re(s) >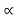 
max. Where 
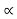max equals to the maximum real part of any poles of X(s).
Property 5:
If x(t) is left-sided that is x(t) =0 for t>t1 >- ∞. Then the ROC is of the form Re(s) < >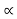 
min.
Property 6:
If x(t) is two-sided than the ROC is of the form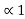 
< Re(s) < 
Find the Laplace transform of the signal
x(t) = e -3t u(t) + e -2t u(t) and find the ROC
What are the pole-zero location.
X(s) =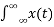 
e -st dt
e -3t u(t) e -st dt + 
e -2t u(t) e -st dt
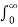e –(s+3) t dt + 
e –(s+2)t dt
Converges if Re(s) >-3 and converges if Re(s) > -2
X(s) = -1/s+3 e –(s+3) t | 0 ∞ + -1/s+2 e –(s+2)t | 0 ∞
= 1/s+3 + 1/ s+2 ROC : Re(s) >-2
= 2s + 5 / s2 +5s + 6 ROC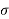 
> -2
The poles are obtained (s+2)(s+3) at s=-2 and s=-3. and zero is at s=-5/2.
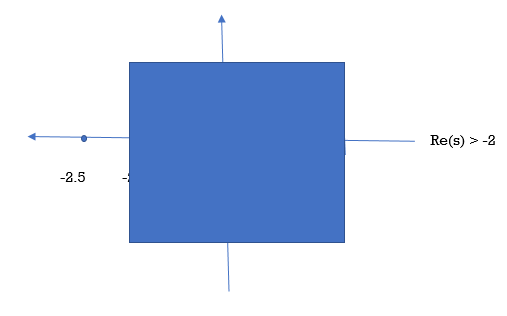
ROC are always vertical half plane stripes bounded by poles.
Right side signals -> ROC in right half plane
Left side signals -> ROC in left half plane
Double sided signals -> ROC in a central stripe or does not exist.
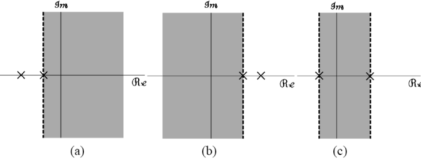
XX(s) = s+3/ (s+1) (s-2) = A/ s+1 + B/s-2
AA = -2/3 B = 5/3
1/s + 1 = e-t
1/ s-2 = e 2t
ROC: Left sided signal
ROC: Two -sided signal
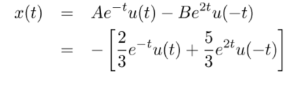
ROC: Right sided signal
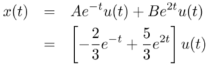
All Laplace transforms in the above examples are rational, i.e., they can be written as a ratio of polynomials of variable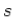 
in the general form
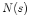is the numerator polynomial of order 
with roots 
,
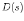is the denominator polynomial of order 
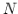with roots 
.
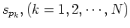In general, we assume the order of the numerator polynomial is always lower than that of the denominator polynomial,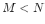 
. If this is not the case, we can always expand 
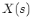into multiple terms so that 
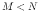is true for each of terms.
Example:
X(s) = s2 – 2s + 2 / s3 + 5s2 + 12 s + 8
= s2 – 2s + 2 / (s+1) ( s2 + 4s + 8)
= [ s-(1+j)] [ s-(1-j)] / [ s-(-1)][s-(-2 + 2j) ][s-(-2 -2j)]
Two zeros: s1 = 1+j s2 = 1-j
Three poles sp1 = -1, sp2 = -2+2j and sp3 = -2 -2j
Example:
X(s) = s2 -3/ s+2
As the order of the numerator M=2 is higher than that of denominator N=1 we expand the following terms
X(s) = s2 -3 / s+2 = A + Bs + C/ s+2
And get
s2 – 3 / s+2 = A + Bs + C/ s+2
And get
s2 – 3 = (A+Bs)(s+2) + C = B s2 + (A+2B ) s + (2A + C)
Equating the coefficients for terms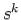 
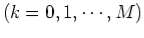on both sides, we get
Solving this equation system, we get coefficients
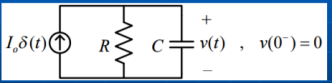
In time-domain
At t=0 , v(0-) = 0
Therefore v(0) = 0 short circuit.
v(0+) = 1/C 
∂(x) dx = Io/C
The impulse current source has stored energy. ½ C ((v(0+)) 2 in capacitor as an initial voltage in an infinitesimal moment.
For t>0+ , ∂ (t) = 0 open circuit.
C dv/dt + v/R =0 natural response
v(0+) = Io/C
v(t) = Io/C e -t/τ u(t) , τ = RC
In s-domain
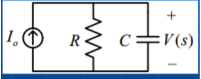
V(s) = Io R x 1/Cs / R + 1/Cs = Io/C / s + 1/RC
v(t) = Io/C e -t/τ u(t) ; τ = RC
Impulse caused by switching operation. The switch is closed at t=0 in the following circuit.
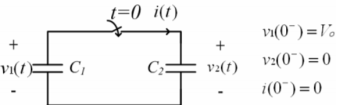
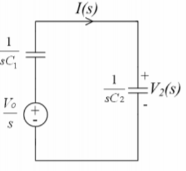
I(s) = Vo/s / 1/sC1 + 1/sC2 x Vo Ce
Ce = C1 . C2 / C1 + C2 ; V2(s) = Vo. Ce / sC2 = Vo/s . C1/C1 + C2
Therefore i(t) = Vo Ce ∂(t)
v2(t) = C1 / C1 + C2 Vo
At t=0 a finite charge of C1 is transferred to C2 instantaneously.
When the switch is closed the voltage across C2 does not jump to Vo of C1 but to its final value of the two paralleled capacitors.
Q2 = C2 V2 = C1.C2 / C1 + C2 Vo for t>0+
Q1 = C1 V2 = C1 2 / C1 + C2 . Vo ; t > 0+
Q1 + Q2 = c1 Vo ; t>0+
At t=0_ Q1 = C1 Vo; Q2 =0
Q1 + Q2 = C1 Vo
Conservation of charge.
Laplace transform can be used to solve (first‐ and second‐order) differential equations with constant coefficients. The differential equations must be IVP's with the initial condition (s) specified at x = 0.
Method:
For the given IVP apply Laplace transform to both the sides of the differential equation.
This will transform the differential equation to algebraic equation which is unknown.
F(p) is the Laplace transform of desired solution.
Solve the algebraic equation for F(p) and take inverse Laplace transform on bot sides to get the result which is the solution to the original IVP.
Solve the following IVP
y′′−10y′+9y=5t,y(0)=−1y′(0)=2y″−10y′+9y=5t,y(0)=−1y′(0)=2
The first step in using Laplace transforms to solve an IVP is to take the transform of every term in the differential equation.
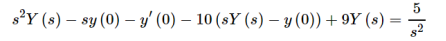
Plug in the initial conditions we get
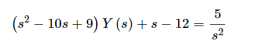
Solve for Y(s)
Combining the two terms we get
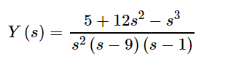
The partial fraction decomposition for this transform is,
Taking the inverse transform gives us the solution to the IVP.
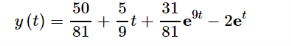
References:
Signals and Systems by Simon Haykin
Signals and Systems by Ganesh Rao
Signals and Systems by P. Ramesh Babu
Signals and Systems by Chitode
