Unit 4
Analysis of Fourier Methods
To represent any periodic signal x(t) Fourier developed an expression called Fourier series. This is in terms of an infinite sum of sines and cosines or exponentials.
A periodic signal is one which repeats itself periodically over -∞ < t < ∞
A sinusoidal signal x(t) = A sin Ω0t is periodic with period T = 2π/ Ω0.
Let us consider a signal x(t) is a sum of sine and cosine functions whose frequencies are integer multiple of Ω0.
x(t) = a0 + a1 cos (Ω0t) + a2 cos (2 Ω0t) + a3 cos ( 3 Ω0t) ……. + ak cos(k Ω0t) + b1 sin(Ω0t) + b2 sin (2Ω0t) + b3 sin(3Ω0t) + ……….. + bk sin( k Ω0t) ------------- (1)
= a0 + 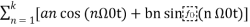
Where a0,a1……. Ak and b1,b2………bk are constants and 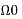 is the fundamental frequency.
is the fundamental frequency.
If the signal x(t) has to be periodic then it should satisfy the condition
x(t + T) = x(t)
x(t + T) = a0 +  ---------------- (2)
---------------- (2)
= a0 + 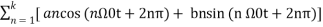 Here
Here 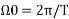
= a0 + 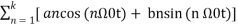 -------------- (3)
-------------- (3)
= x(t)
Evaluation of Fourier Coefficients
The constants a0,a1,a2 ……… an , b1,b2…….bn are called Fourier coefficients. To evaluate ao we have to integrate both sides of eq(3) over one period (t0,t0+T)n of x(t) from an arbitrary time t0.
Thus 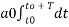 +
+ 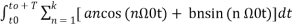 -------(4)
-------(4)
 +
+ 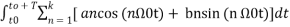 ------(5)
------(5)
= a T + 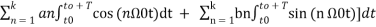 ------(6)
------(6)
Each of the integrals in the summation in the above equation(6) is zero since the net areas of sinusoids over the complete periods are zero for any nonzero integer n .
Therefore
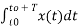 = aoT----------(7)
= aoT----------(7)
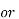 a0 = 1/T
a0 = 1/T  ------(8)
------(8)
To evaluate an and bn
 = 0 for m≠n when m=n ≠0 = T/2.-------(9)
= 0 for m≠n when m=n ≠0 = T/2.-------(9)
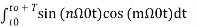 = 0 for values of m and n-------(10)
= 0 for values of m and n-------(10)
 = 0 when m≠n when m=n ≠0 = T/2------(11)
= 0 when m≠n when m=n ≠0 = T/2------(11)
To find an multiply eq(3) by cos(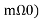 and integrate over one period. That is
and integrate over one period. That is
 +
+ t -----------(12)
t -----------(12)
The first integral on the RHS of the above equation yields to zero because we are integrating over one period.
Therefore
 = am T/2-----(13)
= am T/2-----(13)
Am = 2/T 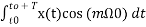 or
or
An = 2/T 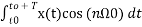
Similarly
Bn=2/T 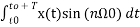
The Fourier series of functions is used to find the steady-state response of a circuit.
There are different types of symmetry that can be used to simplify the process of evaluating the Fourier coefficients.
- Even function symmetry
A function is defined to be even if and only if
f(t) = f(-t)
If a function satisfies the equation then it is said to be even because polynomial functions with only even exponents have this type of behavior.
Av = 2/T 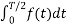
Ak = 4/T  bk=0 for all values of k.
bk=0 for all values of k.
The function is even if the coefficients of b are zero.
When t0 = -T/2 then
Av = 1/T 
Av = 1/T  +
+ 
When t= -x we observe that f(-x) =f(x) since it is even function.
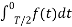 =
= 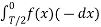 =
= 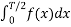
Which does show that integrating from -T/2 to 0 is the same as integrating from 0 to T/2
Therefore
Ak = 2/T  + 2/T
+ 2/T 
 =
= 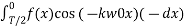 =-
=- 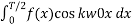
Similarly
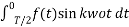 =
= 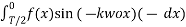 =
= 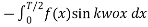
To find the Fourier coefficients the integration lies between 0 and T/2.
- Odd function symmetry
A periodic function is defined to be odd if f( t) = -f(t) due to the fact that polynomial functions with only odd exponents behave this way.
The expression is
Av= 0 ; ak = 0 for all k;
Bk = 4/T 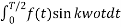

The evenness (oddness) of a function can be dismantled by shifting the periodic function along the time axis.
Example:
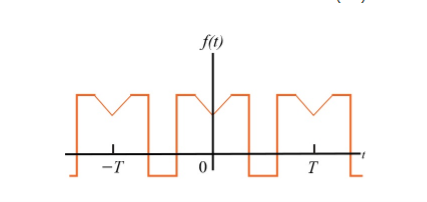
For the following diagram explain whether it is even or odd.

Solution:
The signal is neither even nor odd.
To make the signal even there is a slight shift to be applied as shown in the figure.
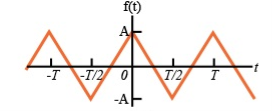
To make the signal odd
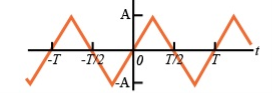
- Half-wave symmetry:
A periodic signal satisfying the condition
x(t) = -x(t ± T/2)
Is said to half symmetry. The Fourier series expansions of such type of periodic signals contains odd harmonics only.
Example:
Show that the signal x(t) that satisfies half wave symmetry contains Fourier coefficients with odd harmonics only.
A signal with half-wave symmetry that satisfies the condition x(t+T/2) = - x(t)
The Fourier coefficients of the signal are
Cn = 1/T 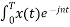 Ω0 dt
Ω0 dt
= 1/T [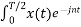 Ω0 dt +
Ω0 dt + 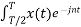 Ω0 dt
Ω0 dt
= 1/T 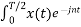 Ω0 dt +
Ω0 dt +  Ω0 dt
Ω0 dt
= 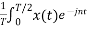 Ω0 dt -
Ω0 dt - 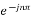
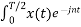 Ω0 dt
Ω0 dt
Here e-jnπ = 1 for n
Even.
Hence Cn=0
Ω0 = 2π/T
- Quarter-wave symmetry
If a function has half-wave symmetry and symmetry about the midpoint of the positive and negative half-cycles, the periodic function is said to have quarter--wave symmetry.
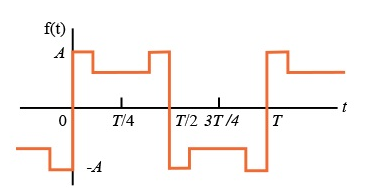
Problems:
Find the trigonometric Fourier series for a square wave periodic signal x(t).
For the given signal the period T =4.
For our convenience let us choose one period signal from t= -1 to t=3
That is t0=-1 and t0+ T =3.
The fundamental frequency
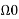 = 2 π/T =2 π/4= π/2.
= 2 π/T =2 π/4= π/2.
x(t) = { 1 for -1 ≤t ≤1
-1 for 1≤t≤3}
a0= 1/T 
= ¼  = ¼[
= ¼[  +
+  ]
]
= ¼ [ t |-1 1 + (-t)| 1 3 ]
= ¼ [ 1 – (-1) – (3-1)] = 0
a0 = 0.
An = 2/T 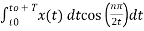
½ 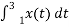
= ½ 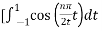 +
+ 
= ½ [ 2/ nπ sin(nπ/2t) | -1 1 - 2/nπ sin(nπ/2t)|1 3
= ½ [ 8/nπ sin(nπ/2)] = 4/nπ sin(nπ/2)
An=4/nπ sin(nπ/2)
Bn = 1/2 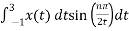
= ½ 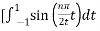 +
+ 
= ½ [ -2 /nπ cos(nπ/2t) | -1 1 + 2/nπ cos(nπ/2t) | 1 3
= -2/nπ(cosnπ/2 – cos nπ/2) + 2/nπ (cos 3nπ/2 – cosnπ/2)
= 0
Therefore 4/nπ sinnπ/2 = { 0 n even
4/nπ = 1,,9,13…..
- 4/nπ 3,7,11,15…….
x(t) = 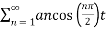
= 4/π cos (π/2 t) – 4/3π cos (3π/2 t)+ 4/5π cos(5π/2 t) - …………..
= 4/π [ cos(π/2 t) -1/ 3 cos( 3π/2 t ) + 1/5 cos (5 π/2 t) – 1/7 cos(7π/2 t) + ………..
The exponential Fourier series is another form of Fourier series. Using Euler’s identity we can write
An cos(Ω0nt + 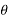 n ) = An [ ej(Ω0nt +
n ) = An [ ej(Ω0nt + 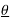 n) –e -j(Ω0nt +
n) –e -j(Ω0nt + 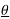 n)]
n)]
2
x(t) = A0 +  ej(Ω0nt +
ej(Ω0nt +  n) –e- j(Ω0nt +
n) –e- j(Ω0nt + 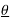 n)]
n)]
= A0 +  e j(Ωont) ejƟn – e - j(Ωont) e j(-Ɵn)
e j(Ωont) ejƟn – e - j(Ωont) e j(-Ɵn)
= A0 + 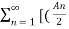 ej
ej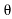 n ) ej(Ω0nt ) + (An/2 e-j
n ) ej(Ω0nt ) + (An/2 e-j 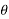 n ) e- j(Ω0t ) ] -------- (1)
n ) e- j(Ω0t ) ] -------- (1)
Let n=-k
x(t) = A0 +  ejƟn ) ej(Ω0nt ] +
ejƟn ) ej(Ω0nt ] + 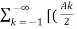 e j Ɵk ) e j(Ω0kt ) ------- (2)
e j Ɵk ) e j(Ω0kt ) ------- (2)
Comparing (1) and (2) we get
An = Ak (-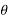 n ) =
n ) =  k n>0 k<0-------------------(3)
k n>0 k<0-------------------(3)
Let us define c0 = A0 ; cn =An/2 ej Ɵn for n>0
By changing the index from k to n and combining into one equation we get
x(t) = A0 + 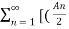 e j ) ej(Ω0nt) +
e j ) ej(Ω0nt) + 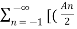 ej
ej n) ej(Ω0nt)]
n) ej(Ω0nt)]
x(t) = 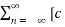 n ej(Ω0nt) ]
n ej(Ω0nt) ]
The above series is known as Exponential Fourier Series.
To develop the coefficients of the the exponential Fourier series
We know that
x(t) =  n ej(Ω0nt) ] where Ω0 = 2π/T
n ej(Ω0nt) ] where Ω0 = 2π/T
Multiply e-jk Ω0 t and integrate over one period .Then
 e-jk Ω0 t dt =
e-jk Ω0 t dt = 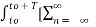 cn ej(Ω0nt) ] e-jk Ω0 t dt
cn ej(Ω0nt) ] e-jk Ω0 t dt
= 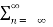 cn
cn  ej(Ω0nt) e-jk Ω0 t dt
ej(Ω0nt) e-jk Ω0 t dt
Substituting the relation  e-jk Ω0 t dt = 0 for k ≠n and T when k=n
e-jk Ω0 t dt = 0 for k ≠n and T when k=n
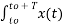 e-jk Ω0 t dt = T ck
e-jk Ω0 t dt = T ck
Therefore
Ck = 1/T 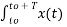 e-jk Ω0 t dt
e-jk Ω0 t dt
Or
Cn = 1/T 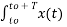 e-jk Ω0 t dt
e-jk Ω0 t dt
Where Cn are the Fourier series coefficients of exponential Fourier series.
Problems:
- Compute the Exponential series of the following series.
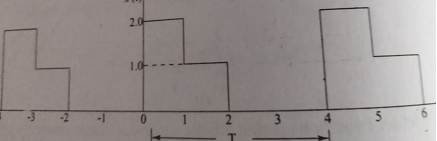
The time period of the signal x(t) is T=4.
Ω0 = 2π/T = 2 π/4= π/2
C0 = 1/T 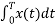 = ¼ [
= ¼ [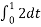 +
+ 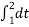
C0 = ¼ [ 2+1 ] = ¾
Cn = 1/T [ 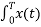 e-jnΩot dt = ¼[
e-jnΩot dt = ¼[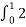 e-jnπ/2t dt +
e-jnπ/2t dt + 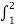 e-jn π/2t dt
e-jn π/2t dt
= ½ . 1/ -jn π/2 [e-jn π/2t ] 0 1 + ¼ 1/-jn π/2[ e-jn π/2t ] 1 2
= - 1/jn π[e-jn π/2 – 1] – 1/ 2jn π (e-jn π – e-jn π/2 )
= 1/jn π[ 1 - e-jn π/2 ] – 1/ 2 e-jn π + ½ e-jn π/2 )
= 1/jn π [ 1- ½ (-1) n -1/2 e-j n π/2 ]
Fourier Integral
The formula for the decomposition of a non- periodic function into harmonic components whose frequencies range over a continuous set of values.
If a function f(x) satisfies the Dirichlet condition on every finite interval and if the integral
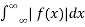 converges then
converges then
F(x) = 1/π 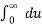
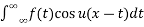 --------- (1)
--------- (1)
The formula was first introduced by J. Fourier in connection with the solution of certain heat conduction problems but was proved later by other mathematicians.
Formula (1) can also be given in the form
f(x) =  ------- (2)
------- (2)
Where
a(u) = 1/π 
b(u) = 1/π 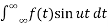
In particular for even functions
f(x) = 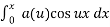 where
where
a(u) = 2/π 
By taking the limits of Fourier series for functions with period 2T as T -> ∞
Then a(u) and b(u) are analogues of the Fourier coefficients of f(x)
Using complex numbers, we can replace formula (1) with
f(x) = 1/2π 
 e ju(x-t) f(t)
e ju(x-t) f(t)
f(x)= lim 1/π 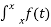 sin
sin  dt
dt
x-t
This is called Fourier Integral.
Problem:
1.Find the Fourier integral of
f(x) = |sin x| |x| ≤ π
= 0 |x| ≥ π
Deduce that  π +1/ 1 -
π +1/ 1 - 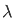 2 cos (
2 cos (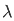 π/2) d
π/2) d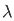 = π/2
= π/2
Solution:
f(x) = 2/π 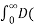
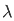

=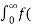 t
t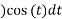 =
= 
=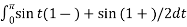
= - cost(1- ) ]0 π - cost(1+
) ]0 π - cost(1+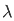 ) ]0 π
) ]0 π
2(1-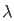 ) 2(1+
) 2(1+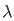 )
)
= 1/ 1- 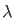 2 [cos π
2 [cos π + 1]
+ 1]
=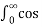 π +1/ 1 -
π +1/ 1 -  2 cos (
2 cos (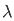 π/2) d
π/2) d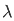 = π/2
= π/2
Find the Fourier Integral of
f(x) = 1 |x| ≤ 1
0 |x| ≥ 1
f(x) = 1/π 
 (t-x) dt d
(t-x) dt d
= 1/π 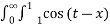 dt d
dt d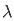
= 1/π /
/ 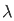 ] -1 1 d
] -1 1 d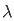
= 1/π  -
- 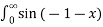 /
/  d
d 
= 1/π 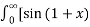 – sin
– sin 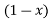 ]/
]/ 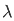 d
d 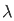
= 2/π 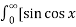 /
/  d
d = π/2 when |x| < 1 and 0 when |x| >1
= π/2 when |x| < 1 and 0 when |x| >1
By setting x=0
= 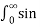 /
/ 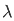 d
d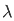 = π/2.
= π/2.
Fourier Transform
Consider a periodic signal f(t) with period T. The complex Fourier series representation of f(t) is given as
f(t) =  k ejkw0t
k ejkw0t
= 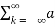 k ej2π/T0kt -------- (1)
k ej2π/T0kt -------- (1)
Let 1/T0 = 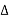 f then equation (1) becomes
f then equation (1) becomes
f(t) = 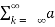 k ej2π
k ej2π kft --------------- (2)
kft --------------- (2)
But you know that
Ak = 1/ T0 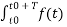 e-jkw0t dt
e-jkw0t dt
Substitute in eq(2)
f(t) = 
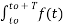 e-jkw0t dt ej2πk
e-jkw0t dt ej2πk 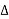 ft
ft
Let to = T/2 then
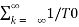
 e-j2πkt
e-j2πkt  dt ej2πkt
dt ej2πkt 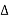 ft
ft 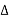 f
f
As lim T-> ∞ 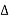 f approaches differential df, k
f approaches differential df, k 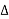 f becomes continuous variable hence summation becomes integration
f becomes continuous variable hence summation becomes integration
f(t) = lim T-> ∞ { 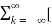
 e-j2πk
e-j2πk 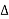 ft dt] ej2πk
ft dt] ej2πk 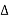 ft
ft  f
f
= 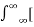
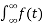 e-j2π ft dt] ej2π ft df
e-j2π ft dt] ej2π ft df
f(t)= 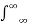
 ejwt dw
ejwt dw
Where F(w) =  e-j2π ft dt
e-j2π ft dt
Fourier transform of a signal is given by
f(t) = F(w) = 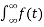 e-jwt dt
e-jwt dt
And Inverse Fourier transform is given by
f(t) = 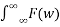 ejwt dw
ejwt dw
If x1(t) and x2(t) are both periodic with period T and the Fourier series co-efficient of x1(t) and x2(t) are cn and dn respectively then
FS[x1(t) x2(t) ] = 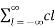 dn-l
dn-l
Proof:
FS[x1(t) x2(t) ] = 1/T 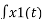 x2(t) e – jnΩot dt ------------------------(1)
x2(t) e – jnΩot dt ------------------------(1)
Using synthesis equation, we write
x 1 (t) =  l e jlΩot --------------------------------------(2)
l e jlΩot --------------------------------------(2)
x 2(t) =  k e jkΩot ---------------------------------------(3)
k e jkΩot ---------------------------------------(3)
Substituting (2) and (3) in (1) we get
FS[x1(t) x2(t) ] = 1/T  l e jlΩot
l e jlΩot 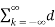 k e jkΩot e – jnΩot dt-----------------(4)
k e jkΩot e – jnΩot dt-----------------(4)
= 1/T = 1/T  l e jlΩot d k e jkΩot e – jnΩot dt --------------------(5)
l e jlΩot d k e jkΩot e – jnΩot dt --------------------(5)
=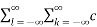 l d k ∂ (n –(k+l)) -------------------------------(6)
l d k ∂ (n –(k+l)) -------------------------------(6)
= 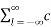 l d n-l ------------------------------------------(7)
l d n-l ------------------------------------------(7)
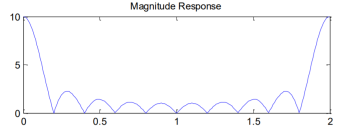
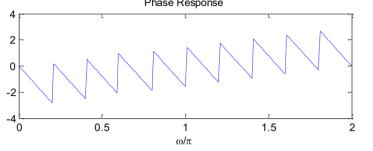
The magnitude and phase response of DTFT is given by
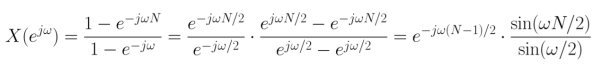
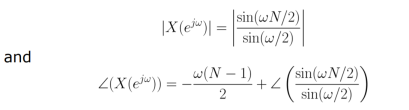
Discrete Fourier Transform
The discrete-time Fourier transform (DTFT) or the Fourier transform of a discrete–time sequence x[n] is a representation of the sequence in terms of the complex exponential sequence ejωn.
The DTFT sequence x[n] is given by
X(w) = 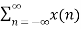 e-jwn ---------------(1)
e-jwn ---------------(1)
Here X(w) is a complex function of real frequency variable w and can be written as
X(w) = Xre (w) + j X img(w)
Where Xre (w) , j X img(w) are real and Imaginary parts of X(w)
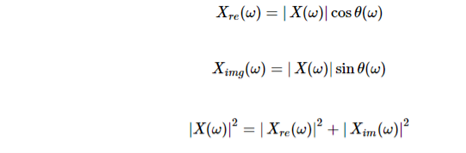
And | X(w)| can be represented as
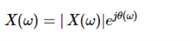 .
.
Inverse Discrete Fourier Transform is given by

Problems:
Find the four point DFT of the sequence
x(n) = {0,1,2,3}
Here N=4. W40 = e-j2πn/4 = e-j π/ 2 = cos 0 – j sin = 1 for n=0
W41 = e-j2 π/4 = cos π/2 – j sin π /2 = -j
W42 = e-j π = cos π – j sin π = -1
W43 = e-j2.3 π/4 = cos 3 π/2 – j sin 3 π/2 = j
For k=0
X(k) = 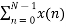 e-j2 π nk/N
e-j2 π nk/N
X(0) =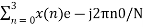
X(0) = x(0)+ x(1)+x(2) + x(3) = 0 +1+2+3 = 6
X(1) = 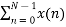 e-j2 π nk/N
e-j2 π nk/N
X(1) = 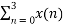 e-j2 π n/4
e-j2 π n/4
= x(0) e0 + x(1) e –j2 π /4+ + x(2) e-j4 π/4+ x(3) e- j 6 π/4
= 0 + 1 –j + 2( -1) + 3(j)
= -2+ 2j
X(2) = 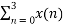 e-j2 π n2/4
e-j2 π n2/4
X(2) = 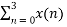 e-j π n
e-j π n
X(2) = x(0) 1+ x(1) e-j π + x(2) e-j2 π + x(3) e-j3 π
X(2) = -2
X(3) =  e-j2 π n3/4
e-j2 π n3/4
X(3) = x(0) e0 + x(1) e-j3 π/2 + x(2) e-j3 π + x(3) e-j9 π/2
X(3) = -2-2j.
DFT = { 6, -2+2j,-2,_2-2j}
Consider two periodic signals x1(t) and x2(t) with equal period T. If the Fourier series co-efficient of these two signals are cn and dn then
1/T 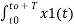 x2(t) = 1/T
x2(t) = 1/T 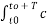 n e j n Ωot [
n e j n Ωot [  m e jmΩot ] dt---------------------(1)
m e jmΩot ] dt---------------------(1)
= 1/T 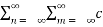 n d *m
n d *m  e j(n-m)Ωot dt ------------------------------(2)
e j(n-m)Ωot dt ------------------------------(2)
= 0 n≠ m
= 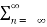 n d *n n=m --------------------------------(3)
n d *n n=m --------------------------------(3)
If x1(t) = x2(t) = x(t) then eq(3) becomes
1/T 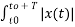 2 =
2 =  2 --------------------------------(4)
2 --------------------------------(4)
The above equation can be written as
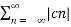 2 = c0 2 +
2 = c0 2 +  2
2
n≠0
= c0 2 + 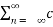 n c *n
n c *n
n≠0
a0 2 + 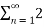 [Re(c 2 n ) + Im (cn ) 2]
[Re(c 2 n ) + Im (cn ) 2]
= a0 2 + 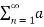 2 n /2 + b 2 n /2 ---------------------------(5)
2 n /2 + b 2 n /2 ---------------------------(5)
References :
Signals and Systems by Simon Haykin
Signals and Systems by Ganesh Rao
Signals and Systems by P. Ramesh Babu
Signals and Systems by Chitode