Unit 5
Z- transformation
The Z transform for discrete time system x(n ) is defined as
X(z) = 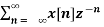 ------- (1) where z is a complex variable.
------- (1) where z is a complex variable.
In polar form z can be expressed as
z = r e jw ---------------(2) where r is the radius of a circle.
For n≥ 0
X(z ) = 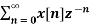 --------- (3)which is called one-sided z-transform.
--------- (3)which is called one-sided z-transform.
By substituting z = r e jw
X(r e jw) = 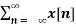 (r e jw) –n ------- (4)
(r e jw) –n ------- (4)
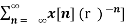 e- jwn ----- (5)
e- jwn ----- (5)
Equation(5) represents the Fourier transform of the signal x(n) r-n
Hence the inverse DTFT X(r ejw) must be x(n) r-n.
x(n) r-n = 1/2π 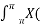 r e jw ) e jwn dw
r e jw ) e jwn dw
On multiplying both sides by rn we get
x(n) = 1/ 2 π 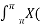 r ejw) (r ejw ) n dw [ z = r ejw
r ejw) (r ejw ) n dw [ z = r ejw
Let z= r e jw and dw= dz/jz
Dz = r ejw dw
Dw = dz/jre jw
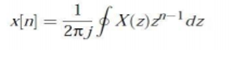
Example
Find the z-transform for the sequence
x[n] = 2  + 3
+ 3 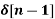 + 5
+ 5 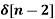 + 2
+ 2 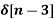
Solution:
X(z) = 2 + 3 z-1 + 5 z -2 + 2 z -3
Example
If X(z)= 4 – 5 z-2 + z-3 – 2z -4 then find x[n]
Solution:
x[n] = 4 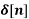 - 5
- 5 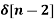 +
+ 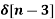 - 2
- 2 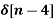
For discrete time LTI system with Impulse response h[n]
For input z n
The output response y[n] = H(z) z n
Where
H(z) = 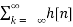 z -n
z -n
The Z-transform of general discrete time signal x[n] is defined as
X(z) = 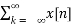 z -n
z -n
The z-transform can be used to convert a difference equation into an algebraic equation in the same manner that the Laplace converts a differential equation into an algebraic equation
The difference equation DE contains the unknown function x(n) and shifted versions of it such as x(n−1) or x(n+3). The solution of the equation is the determination of x(t). A linear DE has only simple linear combinations of x(n) and its shifts.
Z transform converts the difference into algebraic equation in z-domain.
Find the impulse response and step response for the following systems:
y(n) = - ¾ y(n-1) + 1/8 y(n-2) = x(n)
y(n) - ¾ y(n-1) + 1/8 y(n-2) = x(n)
Taking z-transform on both sides we get
Y(z) – ¾ [ z-1 Y(z) + y(-1) ] +1/8 [ z-2 Y(z) + z-1 y(-1)+y(-2)] = X(z)
Substituting y(-1)=y(-2)= 0
Y(z) -3/4 z-1 Y(z) + 1/8 z-2 Y(z) = X(z)
Y(z) = 1____________
1- ¾ z-1 + 1/8 z-2
Impulse response
x(n) = 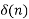 X(z) =1
X(z) =1
Y(z) = 1____________ = 1____________
1- ¾ z-1 + 1/8 z-2 1- ¾ z-1 + 1/8 z-2
Y(z) = z__________ = A___ + B__
X(z) (z-1/2)(z-1/4) (z-1/2) (z-1/4)
By solving A=2 and B=-1.
Y(z) = 2 z - z
z-1/2 (z-1/4)
y(n) = 2 (1/2)n u(n) – (1/4) n u(n).
Step Response
x(n) = u(n) X(z) = z/z-1
Y(z) = 1_______
X(z) 1-3/4 z-1 + 1/8 z-2
Y(z) = z + z2___________
z-1 z2 -3/4 z +1/8
Y(z) = z2___________
z z2 -3/4 z +1/8
Y(z) = z2___________
z (z-1)(z-1/2)(z-3/4)
= A + B + C
z-1 z-1/2 z- 1/4
By solving A=8/3 B= -2 C= 1/3
Therefore
Y(z) = 8 . z -2 z + 1/3 z
3 z-1 z-1/2 z-1/4
y(n) = 8/3 u(n) – 2(1/2)n u(n) +1/3 (1/4) n u(n)
Consider the following diagrams:
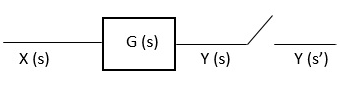
Y( s) = [Y(s)]*
Y(s) = [ X(s) G(s)]*
= [X G(s)]*
Taking z-transform on both sides we get
Y(z) = XG(z)

Y(s) = G1(s) G2(s) X*(s)
Y*(s) = [Y(s)]*
= X*(s) [G1(s)G2(s)]*
= X*(s) [G1G2(s)]*
Y(z) = X(z) G1G2(z)
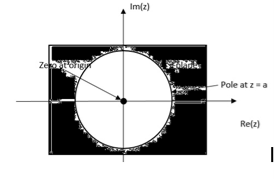
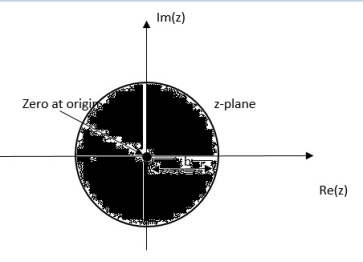
Properties of Region of Convergence
- The ROC is a ring or disk in z-plane centered at the origin.
- The ROC cannot contain any poles.
- If x(n) is finite duration casual sequence then the ROC is the entire z-plane except at z=0.
- If x(n) is a finite duration anti-casual sequence then the ROC is the entire z-plane except at z=∞.
- If x(n) is a finite duration two- sided sequence the ROC is entire z-plane except at z=0 and z=∞.
- If x(n) is infinite duration two- sided sequence ROC will consist of a ring in z-plane bounded on the interior and exterior by a pole not containing any poles.
- The ROC of an LTI stable system contains the unit circle
- ROC must be connected region.
Find the z-transform and ROC of the signal
x(n) = an u(n)
Solution:
X(z) = 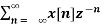
= 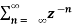 an u(n) -----(1) u(n) = 0 for n<0
an u(n) -----(1) u(n) = 0 for n<0
1 for n≥0
= 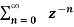 an ------- (2)
an ------- (2)
= 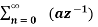 n ------- (3)
n ------- (3)
This is a geometric series of infinite length that is
a + ar + ar2 + ………….. ∞ = a /1-r if |r| <1
Then from equation (3) it converges when |az-1| < 1 or |z| >|a|
Therefore
X(z) = 1/ 1-az-1: ROC |z| > |a|
Find the z-transform of the signal x(n) =-b n u(-n-1). Find ROC
X(z) = 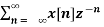
X(z) = 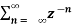 bn u(-n-1) u(-n-1) =0 for n ≥0
bn u(-n-1) u(-n-1) =0 for n ≥0
= 1 for n ≤ -1
= 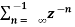 bn =
bn = 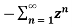 b-1 =
b-1 =
= b-1z/1- b-1z = z/ z-b = 1/ 1-bz-1 |z| < |b|
Find the z-transform of x(n) = an u(n) – bn u(-n-1)
X(z) = 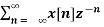
= 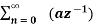 n +
n + 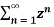 b-1
b-1
= z/z-a + z/z-b ROC |a| < |z| < |b|
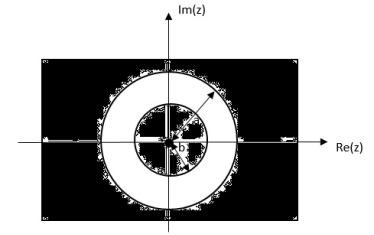
|b|< |a|
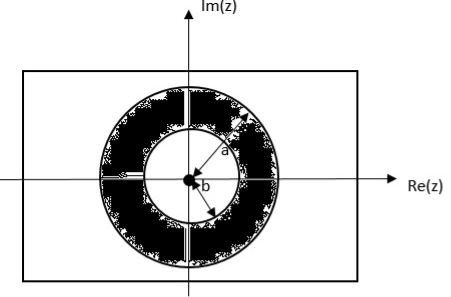
|b| >|a|
A block diagram consists of three elements, that is, the adder, the coefficient multiplier and the delayer. Figure shows these elements.
Example. Suppose that a causal linear time-invariant discrete-time system is characterized by
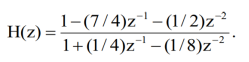
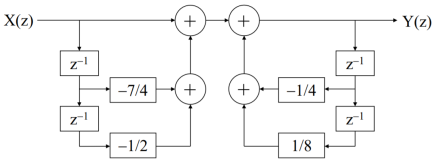
We obtain Y(z)=(1/4)z1Y(z)+(1/8)z2Y(z)+ X(z)(7/4)z1X(z)(1/2)z2X(z).
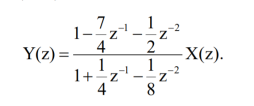
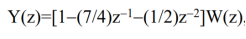

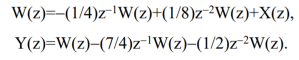

References:
Signals and Systems by Simon Haykin
Signals and Systems by Ganesh Rao
Signals and Systems by P. Ramesh Babu
Signals and Systems by Chitode