Unit - 5
Information Theoretic Approach to Communication System
The meaning of the word “information” in Information Theory is the message or intelligence. The message may be an electrical message such as voltage, current or power or speech message or picture message such as facsimile or television or music message.
A source which produces these messages is called Information source.
Basics of Information System
Information system can be defined as the message that is generated from the information source and transmitted towards the receiver through transmission medium.
The block diagram of an information system can be drawn as shown in the figure.
Information sources can be classified into
- Analog Information Source
- Digital Information Source
Analog Information source such as microphone actuated by speech or a TV camera scanning a scene, emit one or more continuous amplitude electrical signals with respect to time.
Discrete Information source such as teletype or numerical output of computer consists of a sequence of discrete symbols or letters.
An analog information source can be transformed into discrete information source through the process of sampling and quantizing.
Discrete Information source are characterized by
- Source Alphabet
- Symbol rate
- Source alphabet probabilities
- Probabilistic dependence of symbol in a sequence.
In the block diagram of the Information system as shown in the figure, let us assume that the information source is a discrete source emitting discrete message symbols S1, S2………………. Sq with probabilities of occurrence given by P1, P2…………. Pq respectively. The sum of all these probabilities must be equal to 1.
Therefore P1+ P2 + ………………. + Pq = 1----------------------(1)
Or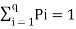 
--------------------(2)
Symbols from the source alphabet S = {s1, s2……………….sn} occurring at the rate of “rs” symbols/sec.
The source encoder converts the symbol sequence into a binary sequence of 0’s and 1s by assigning code-words to the symbols in the input sequence.
Transmitter
The transmitter couples the input message signal to the channel. Signal processing operations are performed by the transmitter include amplification, filtering and modulation.
Channel
A communication channel provides the electrical connection between the source and the destination.The cahnnel may be a pair of wires or a telephone cable or a free space over the information bearing symbol is radiated.
When the binary symbols are transmitted over the channel the effect of noise is to convert some of the 0’s into 1’s and some of the 1’s into 0’s. The signals are then said to be corrupted by noise.
Decoder and Receiver
The source decoder converts binary output of the channel decoder into a symbol sequence. Therefore the function of the decoder is to convert the corrupted sequence into a symbol sequence and the function of the receiver is to identify the symbol sequence and match it with the correct sequence.
Let us consider a zero memory space producing independent sequence of symbols with source alphabet
S = {S1,S2,S3………………Sq} with probabilities P = {P1,P2,P3……..Pq} respectively.
Let us consider a long independent sequence of length L symbols . This long sequence then contains
P1 L number of messages of type S1
P2L number of messages of type S2
……
……
PqL number of messages of type Sq.
We know that the self information of S1 = log 1/P1 bits.
Therefore
P1L number of messages of type S1 contain P1L log 1/P1 L bits of information.
P2L number of messages of type S2 contain P2L log 1/P2L bits of information.
Similarly PqL number of messages of type Sq contain PqL log 1/PqL bits of information.
The total self-information content of all these message symbols is given by
I total = P1L log 1/P1 + P2L log 1/P2 +……….+ PqL log 1/Pq bits.
I total = L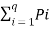 
log 1/Pi
Average self-information = I total /L
= 
log 1/Pi bits/msg symbol.
Average self-information is called ENTROPY of the source S denoted by H(s).
H(s)=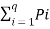 
log 1/Pi bits/message symbol.
Thus H(s) represents the average uncertainity or the average amount of surprise of the source.
Example 1:
Let us consider a binary source with source alphabet S={S1,S2} with probabilities
P= {1/256, 255/256}
Entorpy H(s) =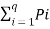 
log 1/Pi
= 1/256 log 256 + 255/256 log 256/255
H(s) = 0.037 bits / msg symbol.
Example 2:
Let S = {S3,S4} with P’ = {7/16,9/16}
Then Entropy H(s’) = 7/16 log 16/7 + 9/16 log 16/9
H(s) = 0.989 bits/msg symbol.
Example 3:
Let S” = {S5,S6} with P” = {1/2,1/2}
Then Entropy H(S”) = ½ log2 2 + ½ log 2 2
H(S”) = 1 bits/msg symbol.
In this case the uncertainity is maximum for a binary source and becomes impossible to guess which symbol is transmitted.
Zero memory space:
It represents a model of discrete information source emitting a sequence of symbols from S= {S1,S2………………….. Sq} successive symbols are selected according to some fixed probability law and are statistically independent of one another. This means that there is no connection between any two symbols and that the source has no memory.Such type of source are memoryless or zero memory sources.
Information rate
Let us suppose that the symbols are emitted by the source at a fixed time rate “rs” symbols/sec. The average source information rate “Rs” in bits/sec is defined as the product of the average information content per symbol and the message symbol rate “rs”
Rs = rs H(s) bits/sec
Consider a source S={S1,S2,S3} with P={1/2,1/4,1/4}
Find
a) Self information
b) Entropy of source S
a) Self information of S1 = I1 = log 21/P1 = Log 2 2 = 1 bit
Self information of S2 = I2 = log 2 1/P2 = Log 2 4 = 2 bits
Self information of S3 = I3 = log 2 1/P3 = Log 2 4 = 2 bits
b) Average Information content or Entropy =
H(s) =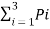 
Ii
= I1 P1 + I2 P2 + I3 P3
= ½(1) + ¼(2) + ¼ (2)
= 1.5 bits/msg symbol.
Q. The collector volatge of a certain circuit lie between -5V and -12V.The voltage can take only these values -5,-6,-7,-9,-11,-12 volts with the respective probabilities 1/6,1/3,1/12,1/12,1/6,1/6. This voltage is recorded with a pen recorder. Determine the average self information associated with the record in terms of bits/level.
Given Q = 6 levels. P= {1/6,1/3,1/12,1/12,1/6,1/6}
Average self-information H(s) =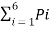 
log 2 1/Pi
= 1/6 log 26 + 1/3 Log 23 + 1/12 log 2 12 + 1/12 log 2 12 + 1/6 Log 26 + 1/6 Log 26
H(s) = 2.418 bits/level
Q. A binary source is emitting an independent sequence of 0s and 1s with probabilities p and 1-p respectively. Plot entopy of source versus p.
The entropy of the binary source is given by
H(s) =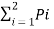 
log 1/Pi
= P1 log 1/P1 + P2 log 1/P2
= P log (1/P) + (1-P) log 1/(1- P)
P=0.1 = 0.1 log(1/0.1) + 0.9 log(1/0.9)
= 0.469 bits/symbol.
At p=0.2
0.2 log(1/0.2) + 0.8 log(1/0.8)
= 0.722 bits/symbol.
At p=0.3
0.3 log(0.3) + 0.7 log(1/0.7)
= 0.881 bits/symbol.
At p=0.4
0.4 log(0.4) + 0.6 log(1/0.6)
= 0.971 bits/symbol.
At p=0.5
0.5 log(0.5) + 0.5 log(1/0.5)
= 1 bits/symbol.
At p=0.6
H(s) = 0.6 log (1/0.6) + 0.4 log(1/0.4)
H(s) = 0.971 biys/symbol
At p=0.7
0.7 log(1/0.7) + 0.3 log(1/0.3)
= 0.881 bits/symbol.
At p=0.8
0.8 log (1/0.8) +0.2 log(1/0.2)
0.722 bits/symbol
At p=0.9
0.9 log(1/0.9) + 0.1 log(1/0.1)
=0.469 bits /symbol.
Q. Let X represent the outcome of a single roll of a fair die. What is the entropy of X?
Since a die has six faces , Probability of getting any number is 1/6.
Px = 1/6.
So entropy of X = H(X) = Px log 1/Px = 1/6 log 6 = 0.431 bits / msg symbol.
Q. Find the entopy of the source in bits/symbol of the source that emits one out of four symbols A,B,C and D in a statistically independent sequences with probabilities ½,1/4,1/8 and 1/8 .
The entropy of the source is given by
H(s) =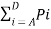 
log 1/Pi
= Pa log 1/Pa + Pb log 1/Pb + Pc log 1/Pc + Pd log 1/Pd
= ½ log 2 2 + ¼ log 2 4 + 1/8 log 2 8 + 1/8 log 2 8
H(s) = 1.75 bits/msg symbol.
1 nat = 1.443 bits
1bit = 1/1.443 = 0.693 nats.
Entropy of the souce H(s) = 1.75 X 0.693 =
H(s) = 1.213 nats/symbol.
Properties
- The entropy function for a source alphabet S = {S1,S2,S3 ……………….. Sq} with probability
P = { P1,P2,P3………………….Pq} where q = no of source symbols as
H(s) =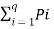 
log (1/Pi) = 
bits/symbol.
The properties can be observed as :
The entropy function is continuous for every independent variable Pk in the interval (0,1) that is if Pk varies continuously from 0 to 1 , so does the entropy function.
The entropy function vanishes at both Pk = 0 and pk =1 that is H(s) = 0.
- The entropy function is symmetrical function of its arguments
H[Pk,(1-Pk)]= H[(1-Pk),Pk]
The value of H(s) remains the same irrespective of the location of the probabilities.
If PA = { P1,P2,P3}
PB = { P2, P3,P1}
PC = { P3,P2,P1}
Then H(SA) = H(SB) = H(SC)
- Extremal Property
Let us consider the source with “q “ symbols S={S1,S2……… Sq} with probabilities P = {P1,P2,………Pq}.Then the entropy is given by
H(s) =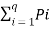 
log 1/Pi -------------------------(1)
And we know that
P1 +P2 + P3 ……………. Pq =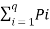 
= 1
Let us now prove that
Log q – H(s) =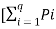 
] log q - 
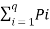log (1/Pi) ]-------------------------(2)
=
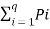[ log q - log (1/Pi)]---------------------------------(3)
=
[ log qPi]----------------------------------(4)
= 
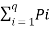[Log e q Pi] / [Log e 2 ]--------------------------(5)
Log q – H(s) = log 2 e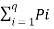 
ln qPi ------------------------------(6)
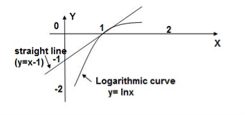
From the graph it is evident that the straight line y=x-1 always lies above the logarithmic curve y = ln x except at x=1. Thus the straight line forms the tangent to the curve at x=1.
Therefor ln x ≤ x-1
Multipling (-1) on both sides we get
-ln x ≥ 1-x or ln 1/x ≥ 1-x -------------------(7)
If X = 1/qp then ln qp ≥ 1 – 1/qp-----------------------(8)
Multipling equation 2 both sides by Pi and taking summation we get for all i=1 to q we get
ln q Pi ≥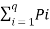 
[ 1 – 1/qPi] ---------------------------(9)
Multiplying eq(3) by log 2 e we get
Log 2 e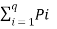 
ln q Pi ≥ Log 2 e [
- 
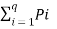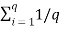-----------------------(10)
From equation (6 )
LHS of log q – H(s) and RHS of eq(6) is zero [ Since [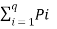
- 
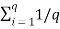=0]
Therefore log q – H(s) = 0
Or H(s) ≤ log 2 q ; Suppose Pi -1/q =0 ; Pi = 1/q for all i=1,2,3………… q which satisfies then
H(s) max = log 2 q bits/msg symbol.
Property of Additivity
Suppose that we split the symbol sq into n sub symbols such that sq = sq1,sq2……….sqn with probabilities Pq1,Pq2,Pq3………………………….. Pqn such that
Pqj = Pq1 + Pq2 + Pq3 +………………….. +Pqn = 
Then the splitted symbol entropy is
H(s’) = H(P1,P2,P3………Pq-1,Pq1,Pq2………Pqn)
= 
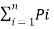log (1/Pi) + 
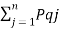log 1/Pqj
H’(s) =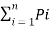 
log (1/Pi) – 
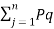log 1/Pq + 
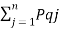log 1/Pqj
H’(s) =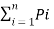 
log (1/Pi) + 
[log 1/Pqj- [log 1/Pq]
= 
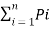log (1/Pi) + Pq 
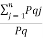[ log Pq/Pqj]
H(s) = H(s)
Therefore H’(s) ≥ H(s)
That is partitioning of symbols into sub symbols cannot decrease entropy
The source effeciency
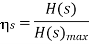
Source Redunancy
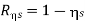
Verify that the rule of additivity for the following source S= {S1,S2,S3,S4} with P={1/2,1/3,1/12,1/12}
The entropy H(s) is given by
H(s) =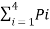 
log 1/Pi
= ½ log 2 2 + 1/3 log 2 3 + 2 x 1/12 log 2 12
H(s) = 1.6258 bits/msg symbol.
From additive property we have
H’(s) = P1 log (1/P1) + (1-P1) log 1/(1-P1)
= (1-P1){ P2/(1-P1) log (1-P1)/P2 + P3/(1-P1) log(1-P1)/P3 + P4/(1-P1) log (1-P1)/P4
= 1/2 log 2 + ½ Log 2 + ½ { (1/3)/(1/2) log(1/2)/(1/2) + (1/12)/1/2 log(1/12)/(1/2) + (1/12)/(1/2) log (1/2) /(1/12)
H’(s) = 1.6258 bits/symbol.
Q. A discreter message source S emits two independent symbols X and Y with probabilities 0.55 and 0.45 respectively. Calculate the effeciency of the source and its redundancy.
Given H(s) =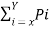 
log 1/Pi
Px log 1/Px + Py log 1/Py
= 0.55 log 1/0.55 + 0.45 log 1/0.45
= 0.9928 bits/msg symbol.
The maximum entropy is given by
H(s) max = log 2 q = log 2 2 = 1 bits/symbol.
The source effeciency is given by
= H(s) max/ H(s) = 0.9928/1 = 0.9928
= 99.28 %
The source redundacy is given by
Rs = 1-
= 0.0072
Rns = 0.72%
Source emcoding is a process in which the output of an information source is converted into a r-ary sequence where r is the number of different symbols used in this transformation process . The functional block that performs this task in a communication system is called source encoder.
The input to the encoder is the symbol sequence emitted by the information source and the output of the encoder is r-ary sequence.
If r=2 then it is called the binary sequence
r=3 then it is called ternary sequence
r=4 then it is called quarternary sequence..
Let the source alphabet S consist of “q” number of source symbols given by S = {S1,S2…….Sq} . Let another alphabet X called the code alphabet consists of “r” number of coding symbols given by
X = {X1,X2………………………Xr}
The term coding can now be defined as the transformation of the source symbols into some sequence of symbols from code alphabet X.
Shannon’s encoding algorithm
The following steps indicate the Shannon’s procedure for generating binary codes.
Step 1:
List the source symbols in the order of non-increasing probabilities
S = {S1,S2,S3……………………Sq} with P = {P1,P2,P3…………………..Pq}
P1 ≥P2 ≥P3 ≥………………….Pq
Step 2
Compute the sequences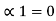 
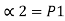= P1 + 
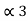= P2 + P1 = P2 + 
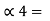P3+P2+P1 = P3 + 
….. ……..
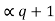= Pq + Pq-1 +…………+ P2 + P1 = Pq +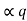 
Step 3:
Determine the smallest integer value of “li using the inequality
2 li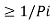 
for all i=1,2,……………………q.
Step 4:
Expand the decimal number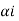 
in binary form upto li places neglecting expansion beyond li places.
Step 5:
Remove the binary point to get the desired code.
Example :
Apply Shannon’s encoding (binary algorithm) to the following set of messages and obtain code efficiency and redundancy.
m 1 | m 2 | m 3 | m 4 | m 5 |
1/8 | 1/16 | 3/16 | ¼ | 3/8 |
Step 1:
The symbols are arranged according to non-incraesing probabilities as below:
m 5 | m 4 | m 3 | m 2 | m 1 |
3/8 | ¼ | 3/16 | 1/16 | 1/8 |
P 1 | P 2 | P 3 | P 4 | P 5 |
The following sequences of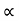 
are computed
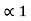= 0
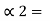P1 +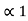 
= 3/8 + 0 = 0.375
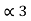= P2 + 
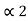= ¼ + 0.375 = 0.625
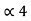= P3 + 
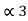= 3/16 + 0.625 = 0.8125
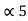= P4 + 
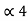= 1/16 + 0.8125 = 0.9375
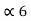= P5 + 
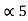= 1/8 + 0.9375 = 1
Step 3:
The smallest integer value of li is found by using
2 li ≥ 1/Pi
For i=1
2 l1 ≥ 1/P1
2 l1 ≥ 1/3/8 = 8/3 = 2.66
The samllest value ofl1 which satisfies the above inequality is 2 therefore l1 = 2.
For i=2 2 l2 ≥ 1/P2 Therefore 2 l2 ≥ 1/P2
2 l2 ≥ 4 therefore l2 = 2
For i =3 2 l3 ≥ 1/P3 Therefore 2 l3 ≥ 1/P3 2 l3 ≥ 1/ 3/16 = 16/3 l3 =3
For i=4 2 l4 ≥ 1/P4 Therefore 2 l4 ≥ 1/P4
2 l4 ≥ 8 Therefore l4 = 3
For i=5
2 l5 ≥ 1/P5 Therefore
2 l5 ≥ 16 Therefore l5=4
Step 4
The decimal numbers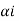 
are expanded in binary form upto li places as given below.
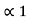= 0
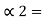0.375
0.375 x2 = 0.750 with carry 0
0.75 x 2 = 0.50 with carry 1
0.50 x 2 = 0.0 with carry 1
Therefore
(0.375) 10 = (0.11)2
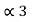= 0.625
0.625 X 2 = 0.25 with carry 1
0.25 X 2 = 0.5 with carry 0
0.5 x 2 = 0.0 with carry 1
(0.625) 10 = (0.101)2
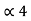= 0.8125
0.8125 x 2 = 0.625 with carry 1
0.625 x 2 = 0.25 with carry 1
0.25 x 2 = 0. 5 with carry 0
0.5 x 2 = 0.0 with carry 1
(0.8125) 10 = (0.1101)2
= 0.9375
0.9375 x 2 = 0.875 with carry 1
0.875 x 2 = 0.75 with carry 1
0.75 x 2 = 0.5 with carry 1
0.5 x 2 = 0.0 with carry 1
(0.9375) 10 = (0.1111)2
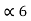= 1
Step 5:
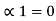and l1 = 2 code for S1 ----00
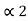=(0.011) 2 and l2 =2 code for S2 ---- 01
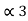= (.101)2 and l3 =3 code for S3 ------- 101
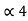= (.1101)2 and l4 =3 code for S ----- 110
= (0.1111)2 and l5 = 4 code for s5 --- 1111
The average length is computed by using
L =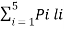 
= 3/8 x 2 + ¼ x 2 + 3/16 x 3 + 1/8 x 3 + 1/16 x 4
L= 2.4375 bits/msg symbol
The entropy is given by
H(s) = 3/8 log (8/3) + ¼ log 4 + 3/16 log 16/3 + 1/8 log 8 + 1/16 log 16
H(s) =2.1085 bits/msg symbol.
Code efficiency is given by
= H(s)/L = 2.1085/2.4375 = 0.865
Percentage code effeciency = 86.5%
Code redundancy
R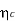
= 1 -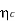 
= 0.135 or 13.5%.
First the source symbols are listed in the non-increasing order of probabilities
Consider the equation
q = r + (r-1 )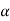 
Where q = number of source symbols
r = no of different symbols used in the code alphabet
The quantity 
is calculated and it should be an integer . If it is not then dummy symbols with zero probabilities are added to q to make the quantity ) 
an integer. To explain this procedure consider some examples.
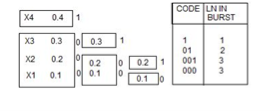
Given the messages X1,X2,X3,X4,X5 and X6 with respective probabilities of 0.4,0.2,0.2,0.1,0.07 and 0.03. Construct a binary code by applying Huffman encoding procedure . Determine the efficiency and redundancy of the code formed.
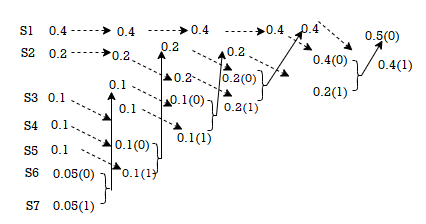
Now Huffmann code is listed below:
Source Symbols | Pi | Code | Length (li) |
X1 | 0.4 | 1 | 1 |
X2 | 0.2 | 01 | 2 |
X3 | 0.2 | 000 | 3 |
X4 | 0.1 | 0010 | 4 |
X5 | 0.07 | 00110 | 5 |
X6 | 0.03 | 00111 | 5 |
Now Average length (L) =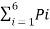 
li
L = 0.4 x 1 + 0.2 x 2 + 0.2 x 3 + 0.1 x 4 + 0.07x 5 + 0.03 x 5
L = 2.3 bits/msg symbol.
Entropy H(s) = =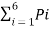 
log 1/Pi
0.4 log 1/0.4 + 0.2 log 1/0.2 + 0.1 log 1/0.1 + 0.07 log 1/0.07 + 0.03 log 1/0.03
H(s) = 2.209 bits /msg symbol.
Code effeciency = nc = H(s) /L = 2.209/2.3 = 96.04%.
Shanon-Fano Encoding procedure for getting a compact code with minimum redundancy is given below:
- The symbols are arranged according to non-increasing probabilities
- The symbols are divided into two groups so that the su of probabilities in each group is approximately equal.
- All the symbols in the first group are designated by “1” and the second group by “0.
- The first group is again subduivided into two subgrous such that rach subgroup probabilities are approximately same.
- All the symbols of the first subgroup are designated by 1 and second subgroup by 0
- The second subgroup is subdivided into two or more subgropus and step 5 is repeated.
- This process is continued till further sub-division is impossible.
Given are the messages X1,X2,X3,X4,X5,X6 with respective probabilities 0.4,0.2,0.2,0.1,0.07 and 0.03. Construct a binary code by applying Shannon-fano encoding procedure . Determine code effeciency and redundancy of the code.
Applying Shannon-fano encoding procedure
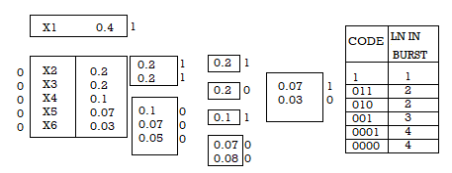
Average length L is given by
L = 
= 0.4 x 1 + 0.2 x 3 + 0.2 x 3 + 0.1 x 3 + 0.07 x4 + 0.03 X 4
L = 2.3 bits/msg symbol.
Entropy
H(s) = 
log 1/Pi
0.4 log 1/0.4 + 2x 0.2 log 1/0.2 + 0.1 log 1/0.1 + 0.07 log 1/0.07 + 0.03 log 1/0.03
H(s) = 2.209 bits/msg symbol.
Code Efficiency = ηc = H(s) / L = 2.209/2.03 = 96.04%
Code Redundancy = R ηc = 1- ηc = 3.96%
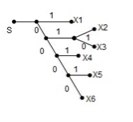
Q. You are given four messages X1 , X2 , X3 and X4 with respective probabilities 0.1,0.2,0.3,0.4
- Device a code with pre-fix property (Shannon fano code) for these messages and draw the code.
- Calculate the efficiency and redundancy of the code.
- Calculate the probabilities of 0’s and 1’s in the code.
Average length L =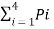 
li
= 0.4 x1 + 0.3 x 2 + 0.2 x 3 + 0.1 x3
L = 1.9 bits/symbol.
Entropy H(s) =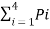 
log 1/Pi
= 0.4 log 1/0.4 + 0.3 log 1/0.3 + 0.2 log 1/0.2 + 0.1 log 1/0.1
H(s) = 1.846 bits/msg symbol.
Code efficiency ηc = H(s) / L = 1.846/1.9 = 97.15%
Code Redundancy = R ηc = 1- ηc = 2.85%
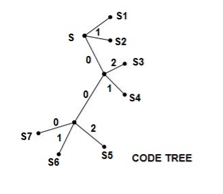
The code tree can be drawn
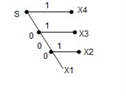
The probabilities of 0’s and 1’s in the code are found by using the
P(0)= 1/L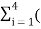 
no of 0’s in code xi) (Pi)
= 1/1.9 [ 3 x 0.1 + 2x 0.2 + 1x 0.3 + 0(0.4)]
P(0) = 0.5623
P(1) = 1/L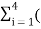 
no of 1’s in code xi) (Pi)
= 1/1.9 [ 0x0.1+1x0.2+1x0.+1x0.4]
P(1) = 0.4737
Shanon –Fano Ternary Code:
The seven steps observed for getting a binary code are slightly modified for ternary code as given below:
- The symbols are arranged according to non-increasing probabilities.
- The symbols are divided into three groups so that the sum of probbilities in each group is approximately equal.
- All the symbols in the first group designated by a “2” , second group by “1” and third group by “0”.
- The first group is again subdivdided into three more sub groups such that each subgroup probabilities are approximately same.
- All the symbols of first subgroup are designated by “2” , the second subgroup by 1 and third subgroup by 0.
- The 2nd and 3rd group are subdivided into three more subgroups each and step 5 is repeated.
- This process is continued till further sub division is impossible.
Q. Construct a Shannon-fano ternary code for the following ensenble and find the code efficiency and redundancy.Also draw the corresponding code tree.
S = { S1,S2,S3,S4,S5,S6,S7}
P={ 0.3,0.3,0.12,0.12,0.06,0.06,0.04} with
X= {0,1,2}
Solution
The average length of the ternary tree is given by
L =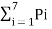 
li -----------------(1)
= 0.3 x 1 + 0.3 x 1 + 0.12 x 2 +0.12 x 2 + 0.06 x3 +0.06x 3 +0.04 x 3
L = 1.56 trinits/msg symbol.
Entropy in bits/msg symbolis given by
H(s) =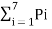 
log 1/Pi
= 0.3 log 1/0.3 x 2 + 0.12 log1/0.12 x2 + 0.06 log 1/0.06 x 2 +0.04 log 1/0.04
= 2.4491 bits/msg symbol.
Now entropy in r-ary units per message symbol is given by
H r (s) = H(s) / log 2 r
r=3
H3 (s) = H(s) / log 2 3 = 2.4419/ log 2 3 = 1.5452.
The terenary coding effeciency is given by
ηc = H3(s) / L = 1.5452/ 1.56 = 0.99 bits/msg symbol.
ηc = 99.05%
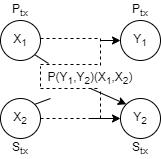
- Communication over a discrete memory less channel takes place in a discrete number of “channel uses,” indexed by the natural number n ∈ ℕ.
- The concepts use the simple two-transmitter, two-receiver channel shown in Figure.
- The primary (secondary) transmitter Ptx (Stx) wishes to communicate a message to a single primary (secondary) receiver Prx (Srx).
- The transmitters communicate their messages by transmitting codewords, which span n channel uses (one input symbol per channel use). The receivers independently decode the received signals, often corrupted by noise according to the statistical channel model, to obtain the desired message.
- One quantity of fundamental interest in such communication is the maximal rate, typically cited in bits/channel use at which communication can take place.
- Most information theoretic results of interest are asymptotic in the number of channel uses; that is, they hold in the limit as n → ∞.
Discrete memory less channel
Mutual information is a quantity that measures a relationship between two random variables that are sampled simultaneously.
It measures how much information is communicated, on average, in one random variable about another.
For example, suppose X represents the roll of a fair 6-sided die, and Y represents whether the roll is even (0 if even, 1 if odd). Clearly, the value of Y tells us something about the value of X and vice versa. That is, these variables share mutual information.
On the other hand, if X represents the roll of one fair die, and Z represents the roll of another fair die, then X and Z share no mutual information. The roll of one die does not contain any information about the outcome of the other die.
An important theorem from information theory says that the mutual information between two variables is 0 if and only if the two variables are statistically independent. The formal definition of the mutual information of two random variables X and Y, whose joint distribution is defined by
I (X; Y) =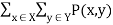 
log P (x.y)/ P(x) P(y)
A channel is said to be symmetric or uniform channel if the second and subsequent rows of the channel matrix contain the same elements as that of the first row but in different order.
For example
P(Y/X) =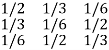 
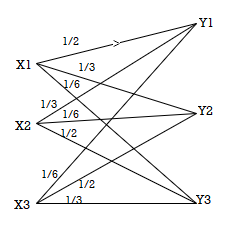
Channel matrix and diagram of symmetric/uniform channel
The equivocation H(B/A) is given by
H(B/A) = 
log 1/P(bi/ai)
But p (ai, bj) = P(ai) P(bj/ai)
H(B/A) =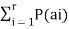 
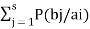log 1/P(bj/ai)
Since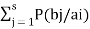 
log 1/P(bj/ai) = h
H(B/A) = 1.h
H=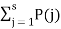 
log 1/P(j)
Therefore, the mutual information I (A, B) is given by
I (A, B) is given by H(B) –H(B/A)
I (A, B) = H(B) –h
Now the channel capacity is defined as
C = Max [I (A, B)]
= Max[H(B) – h]
C = Max[H(b) –h] -----------------------(X)
But H(B) the entropy of the output symbol becomes maximum if and only if when all the received symbols become equiprobable and since there are ‘S’ number of output symbols we have H(B) max = max[H(B) = log s----------------------(Y)
Substituting (Y) in (X) we get
C = log 2 s – h
For the channel matrix shown find the channel capacity
P(bj/ai) =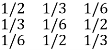 
The given matrix belongs to a symmetric or uniform channel
H(B/A) = h = 
log 1/Pj
= ½ log 2 + 1/3 Log 3 + 1/6 log 6
H(B/A) = 1.4591 bits/msg symbol.
The channel capacity is given by
C = (log S – h) rs rs = 1 msgsymbol/sec
C = log 3 – 1.4591
C = 0.1258 bits/sec
Q. Determine the capacity of the channel as shown in the figure.
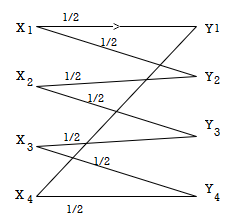
The channelmatrix can be written as
P(Y/X) = ½ ½ 0 0
0 ½ ½ 0
0 0 ½ ½
½ 0 0 ½
Now h = H(Y/X) = 
log 1/Pj
H = ½ log 2 + ½ log 2 +0+ 0 = 1 bits/Msg symbol.
Channelcapacity
C = log s – h
= log 4 – 1
= 1 bits/msg symbol.
Theorem 1 :
Consider a discrete memoryless channel capacity C . For all R<C there exists a sequence of block codes (Cn(M,n) n>0 of rate Rn together with a decoding algorithm such that
Lim n-> ∞ Rn =R and lim n ∞ sup x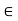 
Cn Pe (Cn,x) = 0
Theorem 2:
Consider a discrete memoryless channel capacity C . Any code C of rate R>C satisfies
1/M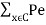 
(C,x) > K(C,R) where K(C,R) >0 depends on the channel and the rate but is independent of the code.
The differential entropy of a continuous random variable X with pdf f(x) is
h(x) = - 
= -E [log(f(x))] --------------------(1)
Definition: Consider a pair of continuous random variable (X,Y) distributed according to the joint pdf (x,y) . The joint entropy is given by
h(X,Y) = -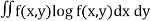 
------------------------------(2)
While the conditional entropy is
h(X|Y) = -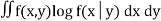 
-----------------------------------------(3)
Shannon-Hartley law states that the capacity of a band limited Gaussian channel with AWGN is given by
C = B log(1+B/N) bits/sec
Where B ----- channel bandwidth in Hz
S ----------------------- signal power in watts
N ------------------------- noise power in watts.
Proof: Consider the channel capacity ‘C’ given by
C = [H(Y) – H(N) ] max------------------------(1)
But
H(N) max = B log 2π e N bits/sec
H(Y) max = B log 2π e 
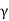2 bits/sec
But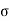 
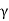2 = S + N
H(Y) max = B log 2π e (S+N) bits/sec
C = = B log 2π e (S+N) - = B log 2π e N
C = B log 2π e (S+N)/ 2π e N
C = B log (S+N)/N
C = B log (1+S/N) bits/sec
1. A voice grade channel of the telephone network has a bandwidth of 3.4KHz
- Calculate the channel capacity of the telephone channel for a signal to noise ratio of 30db
- Calculate the minimum signalto noise ratio required to support information through the telephone channel at the rate of 4800 bits/sec
Given :
Bandwidth = 3.4 KHz
10 log 10 S/N = 30 db
S/N = 10 3 = 1000
Channel capacity
C = B log 2 (1+S/N) = 3400 log (1 + 1000)
C = 33889 bits/sec
Given C = 4800 bits/sec
4800 = 3400 log 2(1+S?N)
S/N = 2 48/34 - 1
S/N = 1.66
S/N = 10 log 1.66 = 2.2 db
S/N = 2.2 db
2. An analog signal has a 4 Khz bandwidth . The signal is sampled at 2.5 times the Nyquist rate and each sample quantized into 256 equally likely levels. Assume that the successive samples are statistically independent.
- Find the information rate of the source
- Can the output of the source be transmitted without error over the Gaussian channel of bandwidth 50Hz and S/N ratio of 20db
- If the output of the source is to be transmitted without errors over an analog channel having S/N of 10 db , Compute bandwidth requirement of the channel.
Given B = 4000Hz Therefore Nyquist rate = 2B = 8000Hz
Sampling rate rs = 2.5 Nyquist rate
= 2.5 x 8000 = 20,000 samples/sec
Since all the quantization levels are equal likely the maximum information content
I = log e q = log 2 256 = 8 bits /sample.
Information rate Rs = rs .I = 20,000 X 8 = 1,60,000 bits/sec
From Shannon’s Hartley law
C = B log (1+ S/N)
C = 332.91 x 10 3 bits/sec
Iii)
C = B log (1+S/N) = Rs
B = Rs/log(1+S/N) = 46.25 KHz
B = 46.25 KHz.
References:
1. Bernard Sklar, Prabitra Kumar Ray, “Digital Communications Fundamentals and Applications”, Pearson Education, 2nd Edition
2. Wayne Tomasi, “Electronic Communications System”, Pearson Education, 5th Edition
3. A.B Carlson, P B Crully, J C Rutledge, “Communication Systems”, Tata McGraw Hill Publication, 5th Edition
4. Simon Haykin, “Communication Systems”, John Wiley & Sons, 4th Edition
5. Simon Haykin, “Digital Communication Systems”, John Wiley & Sons, 4th Edition.
