Unit - 2
Z transform
Due to its convolution property, the z-transform is a powerful tool to analyze LTI systems. From convolution property Y(z)=H(z)X(z).
Where:
Y(z)= z-transform of system output
H(z) = z-transform of impulse response
X(z)= z-transform of system input
A discrete time LTI system is causal if and only if the ROC of its system function is exterior of the circle including infinity. The ROC is the exterior of the outermost pole. H(z) is the ratio of polynomials in z, the order of numerator cannot be greater than the order of the denominator.
The LTI system is stable if and only if the ROC of the system function H(z) includes the unit circle |Z|=1. If it is a causal system, it will be stable if and only if all he poles of H(z) lie inside the unit circle. Section below deals with detailed explanation.
Key takeaway
It is possible for the system to be stable but not causal.
The laplace transform of a signal is given by
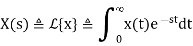
The fourier transform of a signal is given by
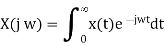
On comparing we get,
Z= esT
The Z transform for discrete time system x(n ) is defined as
X(z) = 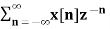 ------- (1) where z is a complex variable.
------- (1) where z is a complex variable.
In polar form z can be expressed as
z = r e jw ---------------(2) where r is the radius of a circle.
For n≥ 0
X(z ) = 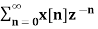 --------- (3)which is called one-sided z-transform.
--------- (3)which is called one-sided z-transform.
By substituting z = r e jw
X(r e jw) = 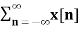 (r e jw) –n ------- (4)
(r e jw) –n ------- (4)
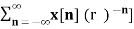 e- jwn ----- (5)
e- jwn ----- (5)
Equation(5) represents the Fourier transform of the signal x(n) r-n
Hence the inverse DTFT X(r ejw) must be x(n) r-n.
x(n) r-n = 1/2π 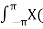 r e jw ) e jwn dw
r e jw ) e jwn dw
On multiplying both sides by rn we get
x(n) = 1/ 2 π 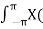 r ejw) (r ejw ) n dw [ z = r ejw
r ejw) (r ejw ) n dw [ z = r ejw
Let z= r e jw and dw= dz/jz
Dz = r ejw dw
Dw = dz/jre jw

- The ROC is a ring or disk in the z-plane centered at the origin.
- ROC cannot contain any poles.
- If x(n) is finite duration casual sequence then the ROC is the entire z-plane except at z=0.
- If x(n) is finite duration anti-casual sequence then ROC is the entire z-plane except at z=∞
- If x(n) is a finite duration two-sided sequence ROC is the entire z-plane except at z=0 and z=∞
- If x(n) is a finite duration two-sided sequence then ROC will consist of a ring in the z-plane bounded on the interior and exterior by a pole not containing any poles.
- The ROC of an LTI system contains unit circle.
- ROC must be a connected region.
Find the z-transform of the signal x(n) = sin w0n u(n) and find ROC.
X(z) = 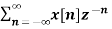
X(z) = 
= 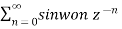 sin
sin  = ej
= ej - e-j
- e-j / 2j
/ 2j
= 1/2j 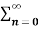 (ejw0n – e –jwon )z-n
(ejw0n – e –jwon )z-n
= 1/2j 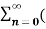 ejwon z-1) n -
ejwon z-1) n - 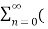 e-jw0z-1) n
e-jw0z-1) n
1/2j[ 1/1-ejw0z-1 – 1/1-e-jw0z-1]
= sin w0 z-1/ 1-2cos(wo)z-1 + z-2 ROC |z| >1
1. Find the z-transform for the sequence
x[n] = 2  + 3
+ 3 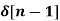 + 5
+ 5 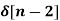 + 2
+ 2 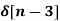
Solution:
X(z) = 2 + 3 z-1 + 5 z -2 + 2 z -3
2. If X(z)= 4 – 5 z-2 + z-3 – 2z -4 then find x[n]
Solution:
x[n] = 4 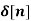 - 5
- 5 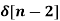 +
+ 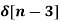 - 2
- 2 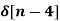
3. Find the z-transform and ROC of the signal
x(n) = an u(n)
Solution:
X(z) = 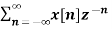
= 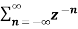 an u(n) -----(1) u(n) = 0 for n<0
an u(n) -----(1) u(n) = 0 for n<0
1 for n≥0
=  an ------- (2)
an ------- (2)
= 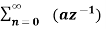 n ------- (3)
n ------- (3)
This is a geometric series of infinite length that is
a + ar + ar2 + ………….. ∞ = a /1-r if |r| <1
Then from equation (3) it converges when |az-1| < 1 or |z| >|a|
Therefore
X(z) = 1/ 1-az-1: ROC |z| > |a|
4. Find the z-transform of the signal x(n) =-b n u(-n-1). Find ROC
X(z) = 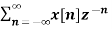
X(z) =  bn u(-n-1) u(-n-1) =0 for n ≥0
bn u(-n-1) u(-n-1) =0 for n ≥0
= 1 for n ≤ -1
= 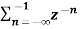 bn =
bn =  b-1 =
b-1 =
= b-1z/1- b-1z = z/ z-b = 1/ 1-bz-1 |z| < |b|
5. Find the z-transform of x(n) = an u(n) – bn u(-n-1)
X(z) = 
= 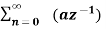 n +
n + 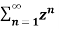 b-1
b-1
= z/z-a + z/z-b ROC |a| < |z| < |b|
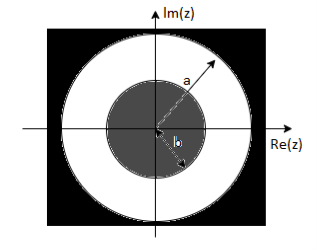
|b|< |a|
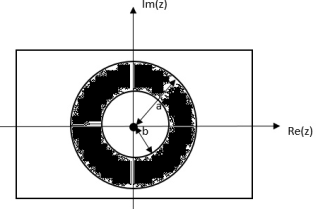
|b| >|a|
6. Find the z-transform of x(n) = {1,2,3,2}
Given x(0) = 1 x(1) =2 x(2) =3 x(3) = 2
X(z) = 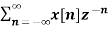
X(z) = 1+ 2z-1 + 3 z-2 +2 z-3
Linearity
If X1(z) = Z{x1(n)} and X2(z) = Z{x2(n)}
Then
Z{ax1(n) + bx2(n)} = a X1(z) + b X2(z)
Proof:
Z{ax1(n) + b x2(n) }= 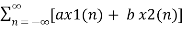 z-n
z-n
= a  z-n + b
z-n + b  z-n
z-n
= a X1(z) + b X2(z)
Time Shifting
If X(z) = Z{x(n)} and initial conditions for x(n) are zero then
Z{x(n-m) } = z-m X(z)
Where m is a positive integer.
Proof:
Z {x(n-m)} = 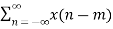 z-n
z-n
Let n-m = p then n= p+m
Z{x(n-m)} =  z –(m+p)
z –(m+p)
z-m 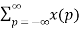 z-p = z-m X(z)
z-p = z-m X(z)
Multiplication by exponential sequence
If X(z ) = Z{x(n)} then
Z [ an x(n) ] = X(a-1 z)
Proof:
Z{ an x(n) } = 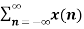 an z-n
an z-n
= 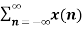 (az-1)n
(az-1)n
= X(az-1)
Convolution
We know that
Z{x(n) * h(n) } = X(z) H(z)
Proof:
Let y(n) = x(n) * h(n)
y(n)= 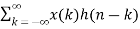
Taking z-transform on both sides we obtain
Y(z) =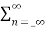
 z-n
z-n
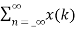 z-k
z-k 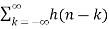 z –(n-k) Replacing n-k by l
z –(n-k) Replacing n-k by l
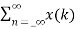 z-k
z-k 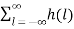 z-l
z-l
= X(k) Z(k)
Time Reversal
If X(z) = Z{x(n)} then
Z{x(-n)} = X(z-1}
Proof:
Z{x(-n)} = 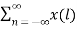 ( z-l) -1 l=-n
( z-l) -1 l=-n
= X(z-1)
Multiplication by n
If Z{x(n)} = X(z) then
Z{n x(n)} = -z d/dz X(z)
X(z) = 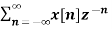
Z{n x(n)} = 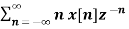
= z 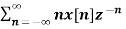 -1
-1
= z 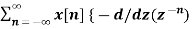
= -z 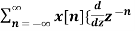 }
}
= -z d/dz { 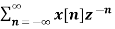
= -z d/dz X(z)
Problems:
- Find the z-transform of the sequence
x(n) = a n-1 u(n-1)
We know that x(n) = an u(n) is
X(z) = 1/1/az-1
By using time shifting property we have Z{ x(n-k)} = z-k X(z)
Therefore
Z{an-1 u(n-1)} = z-1/ 1-az-1 = 1/z-a. ROC |z| > |a|
2. Find the z-transform of the sequence
x(n) = an cos nπ/2
Z{ cos w0n} = 1- (cos w0) z-1/ 1 –(2 cos w0) z-1 + z-2
Since w0=π/2
Z{ cos π/2 n u(n)} = 1/1 + z-2
Using exponential sequence property
Z{ an x(n) } = X(a-1 z)
Z{ an cos nπ/2} = 1/1+(a-1z)-2 = 1/ 1 + a2/z2 = z2/ a2 + z2
3. Find the z transform of the sequence x(n) = n u(n)
The z-transform of unit step sequence is given by
Z{u(n)} = z/z-1
Z{ n u(n)} = -z d/dz (z/z-1)
= z/(z-1)2
4. If x(n) = x1(n) * x2(n) where x1(n) = (1/3)n u(n) and x2(n) = (1/5)n u(n). Find X(z) by using convolution property.
X1(z) = 1/ 1- (1/3)z-1 X2(z) = 1/1- (1/5) z-1
X(z) = 1/1-(1/3)z-1 . 1/1-(1/5) z-1
Using z-transform find the convolution of two sequences.
x1(n) = {1,2,-1,0,3} x2(n) = { 1,2,-1}
Z{ x1(n) * x2(n)} = X1(z) . X2(z)
X1(z) = 1 + 2z-1 – z-2 + 3 z-4
X2(z) = 1 + 2z-1 – z-2
(1 + 2z-1 – z-2 + 3 z-4 ) (1 + 2z-1 – z-2 )
= 1 + 4z-1 + 2z-2 – 4 z- 3 + 4 z-4 + 6 z- 5 – 3 z-6
5. Determine the z-transform of the signal
x(n ) = rn (sin w0n ) u(n)
Z{(sin w0n ) u(n)} = sin w0 z-1/ 1 -2 (cos w0) z-1 + z-2
Z{ an x(n)} = X(a-1 z)
Therefore
Z{ rn sin(w0n) u(n) } = (sin w0) (r-1 z)-1/ 1- 2 (cos w0)(r-1z)-1 + (r-1z)-2
= r(sinw0) z-1/ 1-2r(cos w0) z-1 + r2 z-2
6. Determine the signal x(n) whose z-transform is given by
X(z) = log(1- az-1).
X(z)= log(1-az-1)
Differentiating both sides we get
d/dz X(z) = 1/1-az-1 (a z-2) = az-2/1- az-1
-z d/dz { X(z)} = -az-1/1-az-1
= -az-1[ 1/1-az-1]
= -a Z[ a n-1 u(n-1)] -------- (1)
From differentiation property
Z{ n x(n)} = -z d/dz [ X(z)] ------- (2)
Comparing (1) and (2) we get
n x(n) = -a [ a n-1 u(n-1)]
Or x(n) = -a [a n-1 u(n-1)]/n
7. Determine the z-transform of the signal
x(n) =1/2 (n2 + n) (1/3) n-1 u(n-1)
=½ n2 (1/3) n-1 u(n-1) +1/2 n (1/3) n-1 u(n-1)
We know that
Z[(1/3) n u(n)] = z/ z-1/3
Using time-shifting property
Z{(1/3) n-1 u(n-1)] = 1/ z- 1/3
Z [ n (1/3) n-1 u(n-1)] = -z d/dz [1/z-(1/3)]
=-z d/dz( 1/z-1/3)= -z [-1/(z-1/3) 2]= z/ (z-1/3)2
Z [ n2 (1/3) u(n-1)] = -z d/dz [ z/(z-1/3)2]
= z(z+1/3)/(z-1/3)2
= -z [ (z-1/3)2 -2z(z-1/3)/(z-1/3)4
= z(z+1/3)/(z-1/3)3
X(z) = ½[z(z+1/3)/(z-1/3)3 + z/ (z-1/3)2]
= z2/(z-1/3)3
The roots of a polynomial with real coefficients are either real or complex conjugate pairs. Thus we focus on these cases.
Single Real Pole
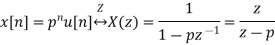
- Signal decays if pole is inside unit circle.
- Signal blows up if pole is outside unit circle.
- Signal alternates sign if pole is in left half plane, since
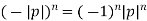
Double Real Pole

As noted previously: 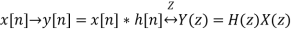
- Forward direction: transform h[n] and x[n] multiply then inverse transform
- Reverse engineering: Put in known signal x[n] with transform X(z); observe output y[n]; complete transform Y(z) .Divide the two to get the system function or transfer function H(z)=Y(z)/X(z)
If you choose any input x[n], what would it be? Probably x[n]= since X(z)=1, so output is directly the impulse response.
since X(z)=1, so output is directly the impulse response.
- The third rearrangement
 is also useful sometimes.
is also useful sometimes.
Now these ideas to the analysis of LTI systems that are described by general linear constant coefficient difference equations
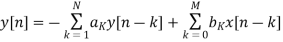
Goal: Find impulse response h[n] .Not simple with time domain techniques. Systematic approach uses z-transforms Applying linearity and shift properties taking z-transforms of both sides of the above:
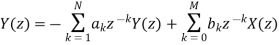
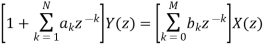
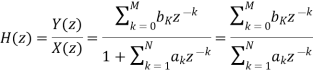
Due to its convolution property, the z-transform is a powerful tool to analyse LTI systems
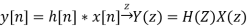
As discussed before, when the input is the eigen function of all LTI system, i.e.,
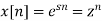
The operation on this input by the system can be found by multiplying the system's eigenvalue H(z) to the input:

Causal LTI systems
An LTI system is causal if its output y(n) depends only on the current and past input x(n) (but not the future). Assuming the system is initially at rest with zero output y(n) =0 for n<0, then its response y(n)=h(n) to an impulse x(n)= δ(n) at n=0 is at rest for n<0, i.e., h(n)= h(n)u(n). Its response to a general input x(t) is:
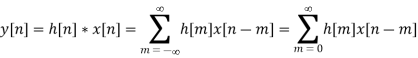
Due to the properties of the ROC, we know that
If an LTI system is causal then the ROC of its transfer function H(z) is the exterior of a circle including infinity. In particular, when H(z) is rational, then the system is causal if and only if its ROC is the exterior of a circle outside the out-most pole, and the order of numerator is no greater than the order of the denominator. Note the requirement for the orders of the numerator and denominator guarantees the existence of H(z) even when z=∞
Stable LTI systems
An LTI system is stable if its response to any bounded input is also bounded for all n
If 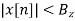 then
then 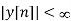
As the output and input of an LTI is related by convolution, we have:

And
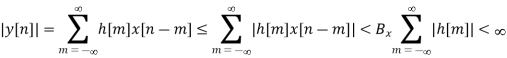
Which obviously requires:

In other words, if the impulse response function h(m) of an LTI system is absolutely integrable, then the system is stable. We can show that this condition is also necessary, i.e., all stable LTI systems' impulse response functions are absolutely integrable. Now we have:
An LTI system is stable if and only if its impulse response is absolutely summable, i.e., the frequency response function H(ejω) exits, i.e. the ROC of its transfer function H(z) includes the unit circle |z| = 1.

Causal and stable LTI systems
From the two properties above, we also see that
A causal LTI system with a rational transfer function H(z) is stable if and only if all poles of H(z) are inside the unit circle of the z-plane, i.e., the magnitudes of all poles are smaller than 1.
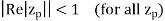
Example:
The transfer function of an LTI is
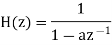
As shown before, without specifying the ROC, this H(z) could be the z-transform of one of the two possible time signals h(n).
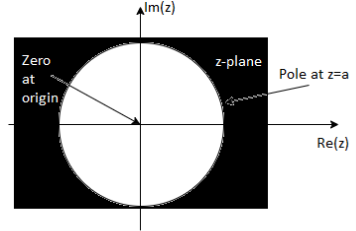
If ROC is |z|>a, the system h[n]=an u[n] is causal.
If |a|<1, i.e., unit circle can be included in ROC, the system is stable
If |a|>1, i.e., unit circle cannot be included in ROC, the system is unstable
If ROC is |z|<|a|, the system h[n]=-an u[-n-1] is anti-causal.
If |a|<1, i.e., unit circle cannot be included in ROC, the system is unstable
If |a|>1, i.e., unit circle can be included in ROC, the system is stable
Key takeaway
| |a|<1 | |a|>1 |
|z|>|a| | ejω inside ROC | ejω outside ROC, |
h[n]=ean u(n) | Causal, stable | Causal, unstable |
|z|<|a| | ejω outside ROC | ejω inside ROC, |
h[n]=-an u[-n-1] | Anti-causal, unstable | Anti-causal, stable |
Z transform converts the difference into algebraic equation in z-domain.
Find the impulse response and step response for the following systems:
y(n) = - ¾ y(n-1) + 1/8 y(n-2) = x(n)
y(n) - ¾ y(n-1) + 1/8 y(n-2) = x(n)
Taking z-transform on both sides we get
Y(z) – ¾ [ z-1 Y(z) + y(-1) ] +1/8 [ z-2 Y(z) + z-1 y(-1)+y(-2)] = X(z)
Substituting y(-1)=y(-2)= 0
Y(z) -3/4 z-1 Y(z) + 1/8 z-2 Y(z) = X(z)

Impulse response
x(n) = 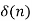 X(z) =1
X(z) =1
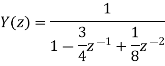
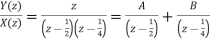
By solving A=2 and B=-1.
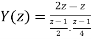
y(n) = 2 (1/2)n u(n) – (1/4) n u(n).
Step Response
x(n) = u(n) X(z) = z/z-1
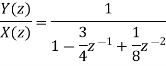
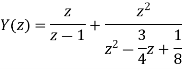
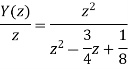
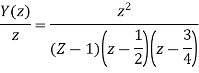
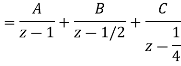
By solving A=8/3 B= -2 C= 1/3
Therefore
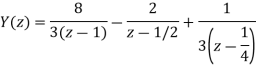
y(n) = 8/3 u(n) – 2(1/2)n u(n) +1/3 (1/4) n u(n)
Consider the following diagrams:
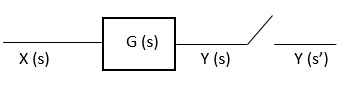
Y( s) = [Y(s)]*
Y(s) = [ X(s) G(s)]*
= [X G(s)]*
Taking z-transform on both sides we get
Y(z) = XG(z)

Y(s) = G1(s) G2(s) X*(s)
Y*(s) = [Y(s)]*
= X*(s) [G1(s)G2(s)]*
= X*(s) [G1G2(s)]*
Y(z) = X(z) G1G2(z)
References:
1. Ifeachor E.C, Jervis B. W, “Digital Signal Processing: Practical approach”, Pearson Publication, 2nd Edition.
2. Li Tan, “Digital Signal Processing: Fundamentals and Applications”, Academic Press, 3rd Edition.
3. Schaum's Outline of “Theory and Problems of Digital Signal Processing”, 2nd Edition.
4. Oppenheim, Schafer, “Discrete-time Signal Processing”, Pearson Education, 1st Edition.
5. K.A. Navas, R. Jayadevan, “Lab Primer through MATLAB”, PHI, Eastern Economy Edition.