Unit - 6
Introduction to 1D & 2D Signal Processing
Gram-schimdt orthogonalization procedure
In mathematics, particularly linear algebra and numerical analysis, the Gram-schmidt process is a method for orthogonlaizing a set of vectors in an inner product space.
We know that any signal vector can be represented interms of orthonormal basis function  . Gram-schimdt orthogonalization procedure is the too to obtain the orthonormal basis function
. Gram-schimdt orthogonalization procedure is the too to obtain the orthonormal basis function 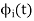
To derive an expression for 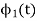
- Suppose we have set of ‘M’ energy signals denoted by
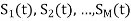 .
. - Starting with
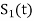 choosen from set arbitrarily the basis function is defined by
choosen from set arbitrarily the basis function is defined by
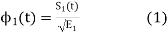 where
where 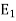 is the energy of the signal
is the energy of the signal  .
.
From equation (1) we can write
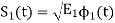 (2) we know that
(2) we know that 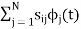 for N=1 eq(1) can be written as
for N=1 eq(1) can be written as  (3)
(3)
From the above equation (3) we obtain 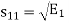 and
and  has unit energy.
has unit energy.
Next using the signal 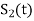 we define the co-efficient
we define the co-efficient  as
as
 (4)
(4)
Let  be a new intermediate function which is given as
be a new intermediate function which is given as
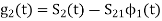 (5)
(5)
The function is orthogonal to 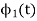 over the interval 0 to T.
over the interval 0 to T.
The second function which is given as
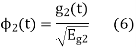

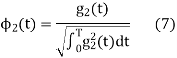
(A) To prove that 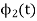 has unit energy
has unit energy
Energy of 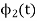 will be
will be 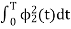
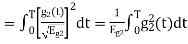
We know that
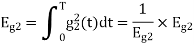
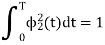
(B) To prove that 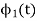 and
and 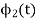 are orthogonal
are orthogonal
Consider 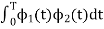
Substitute the values of 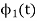 and
and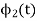 in the above equation is
in the above equation is
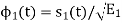 and
and 

Substitute 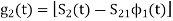
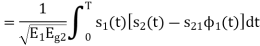
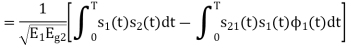
We know that
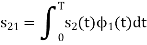
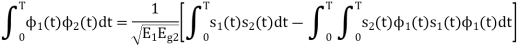
From the given equation there is a product of two terms 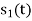 and
and 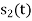 . But the two symbols are not present at a time. Hence the product of
. But the two symbols are not present at a time. Hence the product of 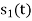 and
and 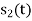 ie
ie  and hence the integration terems in RHS will be zero ie
and hence the integration terems in RHS will be zero ie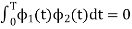
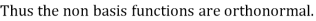
Generalised equation for orthonormal basis funciton
The generalized equation for orthonormal basis function can be written by considering the following equation ie
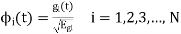
Where 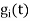 is given by the generalise equation
is given by the generalise equation
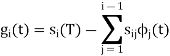
Note:
(i-1) 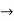
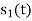 ready taken consideration
ready taken consideration
Where the co-efficients

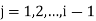
For i=1, the 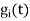 reduces to
reduces to 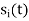
Given the 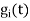 , we may define the set of basis function
, we may define the set of basis function
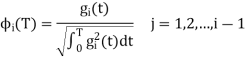
Which from an orthonormal set. The dimension ‘N’ is less that or equal to the number of given signals, M defending on one of two possibilities.
The signals 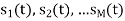 form a linearly indpendent set in which case N=M
form a linearly indpendent set in which case N=M
The signals 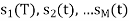 are not linearly indpendent.
are not linearly indpendent.
These are the signals which are function of only one independent variable. These are music, speech or heartbeat. One of the most common examples, of 1D signal is sound from car horn. The sound from horn can be explained as sample of amplitude of sound many times in one second. This approximates the value of sound as function of time. These are called as 1D sounds.
Speech is composed of a sequence of sounds Sounds/Phonemes serve as a symbolic representation of information to be shared between humans (or humans and machines) Arrangement of sounds is governed by rules of language (constraints on sound sequences, word sequences, etc) Linguistics is the study of the rules of language Phonetics is the study of the sounds of speech.

Fig 1 Vocal Tract
Vocal tract —dotted lines in figure; begins at the glottis (the vocal cords) and ends at the lips. Consists of the pharynx (the connection from the oesophagus to the mouth) and the mouth itself (the oral cavity). Average male vocal tract length is 17.5 cm. Cross sectional area, determined by positions of the tongue, lips, jaw and velum, varies from zero (complete closure) to 20 sq cm Nasal tract — begins at the velum and ends at the nostrils Velum —a trapdoor-like mechanism at the back of the mouth cavity; lowers to couple the nasal tract to the vocal tract to produce the nasal sounds like /m/ (mom), /n/ (night), /ng/ (sing).
1.When the vocal cords are tensed, the air flow causes them to vibrate, producing voiced sound.
2. When the vocal cords are relaxed, in order to produce a sound, the air flow either must pass through a constriction in the vocal tract and there by become turbulent, producing unvoiced sound or it can build up pressure behind a point of total closure within the vocal tract and when the closure is opened, the pressure is suddenly and abruptly released, causing a brief transient sound.
The shape of the vocal tract transforms raw sound from the vocal folds into recognizable sounds.
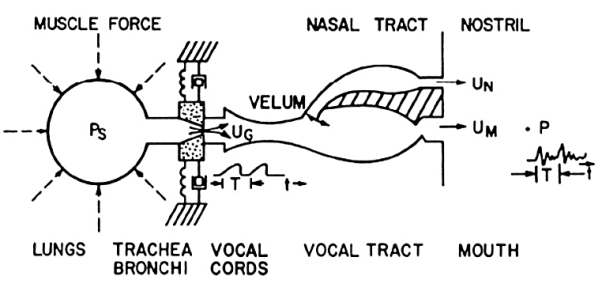
Fig 2 Abstraction of Physical Model
A schematic longitudinal cross-sectional drawing of the human vocal tract mechanism is given in Figure above. This diagram highlights the essential physical features of human anatomy that enter into the final stages of the speech production process. It shows the vocal tract as a tube of nonuniform cross-sectional area that is bounded at one end by the vocal cords and at the other by the mouth opening. This tube serves as an acoustic transmission system for sounds generated inside the vocal tract.
For creating nasal sounds like /M/, /N/, or /NG/, a side-branch tube, called the nasal tract, is connected to the main acoustic branch by the trapdoor action of the velum. This branch path radiates sound at the nostrils. The shape (variation of cross-section along the axis) of the vocal tract varies with time due to motions of the lips, jaw, tongue, and velum. Although the actual human vocal tract is not laid out along a straight line as in Figure above, this type of model is a reasonable approximation for wavelengths of the sounds in speech.
The sounds of speech are generated in the system of Figure above in several ways. Voiced sounds (vowels, liquids, glides, nasals) are produced when the vocal tract tube is excited by pulses of air pressure resulting from quasi-periodic opening and closing of the glottal orifice (opening between the vocal cords). Examples are the vowels /UH/, /IY/, and /EY/, and the liquid consonant /W/.
Unvoiced sounds are produced by creating a constriction somewhere in the vocal tract tube and forcing air through that constriction, thereby creating turbulent air flow, which acts as a random noise excitation of the vocal tract tube. Examples are the unvoiced fricative sounds such as /SH/ and /S/. A third sound production mechanism is when the vocal tract is partially closed off causing turbulent flow due to the constriction, at the same time allowing quasi-periodic flow due to vocal cord vibrations. Sounds produced in this manner include the voiced fricatives /V/, /DH/, /Z/, and /ZH/. Finally, plosive sounds such as /P/, /T/, and /K/ and affricates such as /CH/ are formed by momentarily closing off air flow, allowing pressure to build up behind the closure, and then abruptly releasing the pressure. All these excitation sources create a wide-band excitation signal to the vocal tract tube, which acts as an acoustic transmission line with certain vocal tract shape-dependent resonances that tend to emphasize some frequencies of the excitation relative to others.
The acoustics of male and female vowels differ reliably along two different dimensions:
1. Sound Source
2. Sound Filter
• Source--F0: Depends on length of vocal folds
Shorter in women higher average F0
Longer in men lower average F0
• Filter--Formants: Depend on length of vocal tract
Shorter in women higher formant frequencies
Longer in men lower formant frequencies
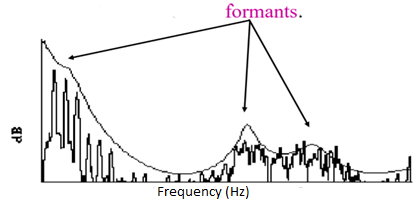
Fig 3 Formant
To identify dissimilar sounds i.e., vowels, the ears are more sensitive to peaks in the signal spectrum. These resonant peaks in the spectrum are called formants. Formants are the characteristics partial that identify vowels to the listeners. Formant with lowest frequency is called F1, the second F2 & the third F3. F1 & F2 are enough to disambiguate the vowel.
Key takeaway
For creating nasal sounds like /M/, /N/, or /NG/, a side-branch tube, called the nasal tract, is connected to the main acoustic branch by the trapdoor action of the velum. This branch path radiates sound at the nostrils. The shape (variation of cross-section along the axis) of the vocal tract varies with time due to motions of the lips, jaw, tongue, and velum.
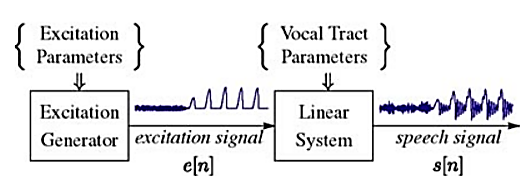
Fig 4 Speech Signal Representation
The discrete-time time-varying linear system on the right in Figure above simulates the frequency shaping of the vocal tract tube. The excitation generator on the left simulates the different modes of sound generation in the vocal tract. Samples of a speech signal are assumed to be the output of the time-varying linear system.
In general such a model is called a source/system model of speech production. The short-time frequency response of the linear system simulates the frequency shaping of the vocal tract system, and since the vocal tract changes shape relatively slowly, it is reasonable to assume that the linear system response does not vary over time intervals on the order of 10 ms or so. Thus, it is common to characterize the discrete-time linear system by a system function of the form:
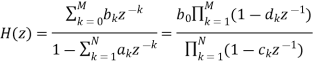
Where the filter coefficients ak and bk (labelled as vocal tract parameters in Figure above) change at a rate on the order of 50–100 times/s. Some of the poles (ck) of the system function lie close to the unit circle and create resonances to model the formant frequencies. In detailed modeling of speech production, it is sometimes useful to employ zeros (dk) of the system function to model nasal and fricative sounds.
The box labelled excitation generator in Figure above creates an appropriate excitation for the type of sound being produced. For voiced speech the excitation to the linear system is a quasi-periodic sequence of discrete (glottal) pulses that look very much like those shown in the righthand half of the excitation signal waveform in Figure above. The fundamental frequency of the glottal excitation determines the perceived pitch of the voice. The individual finite-duration glottal pulses have a lowpass spectrum that depends on a number of factors. Therefore, the periodic sequence of smooth glottal pulses has a harmonic line spectrum with components that decrease in amplitude with increasing frequency. Often it is convenient to absorb the glottal pulse spectrum contribution into the vocal tract system model.
This can be achieved by a small increase in the order of the denominator over what would be needed to represent the formant resonances. For unvoiced speech, the linear system is excited by a random number generator that produces a discrete-time noise signal with flat spectrum as shown in the left-hand half of the excitation signal. The excitation in Figure above switches from unvoiced to voiced leading to the speech signal output as shown in the figure. In either case, the linear system imposes its frequency response on the spectrum to create the speech sounds.
This model of speech as the output of a slowly time-varying digital filter with an excitation that captures the nature of the voiced/unvoiced distinction in speech production is the basis for thinking about the speech signal, and a wide variety of digital representations of the speech signal are based on it. That is, the speech signal is represented by the parameters of the model instead of the sampled waveform. By assuming that the properties of the speech signal (and the model) are constant over short time intervals, it is possible to compute/measure/estimate the parameters of the model by analysing short blocks of samples of the speech signal. It is through such models and analysis techniques that we are able to build properties of the speech production process into digital representations of the speech signal.
Key takeaway
The short-time frequency response of the linear system simulates the frequency shaping of the vocal tract system, and since the vocal tract changes shape relatively slowly, it is reasonable to assume that the linear system response does not vary over time intervals on the order of 10 ms or so.
The fundamental frequency of a speech signal, often denoted by F0 or F0, refers to the approximate frequency of the (quasi-)periodic structure of voiced speech signals. The oscillation originates from the vocal folds, which oscillate in the airflow when appropriately tensed. The fundamental frequency is defined as the average number of oscillations per second and expressed in Hertz. Typically, fundamental frequencies lie roughly in the range 80 to 450 Hz, where males have lower voices than females and children. The F0 of an individual speaker depends primarily on the length of the vocal folds, which is in turn correlated with overall body size.
If F0 is the fundamental frequency, then the length of a single period in seconds is
T=1/f0
The speech waveform thus repeats itself after every T seconds.
A simple way of modelling the fundamental frequency is to repeat the signal after a delay of T seconds. If a signal is sampled with a sampling rate of Fs, then the signal repeats after a delay of L samples where:
L=Fs T= Fs/F0
Key takeaway
If F0 is the fundamental frequency, then the length of a single period in seconds is
T=1/f0
The speech waveform thus repeats itself after every T seconds
Sound is variations in air pressure. The creation of sound is the process of setting the air in rapid vibration. Speech signal is an acoustic signal produced from a speech production system. The system characteristics depend on the design of the system. For the case of LTI system, this is completely characterized in terms its impulse response. However, the nature of output depends on the type of input excitation to the system. For instance, we have impulse response, sinusoidal response and so on for a given system. Each of these output responses are used to understand the behavior of the system under different conditions.
A similar phenomenon happens in the production of speech also. Based on the input excitation phenomenon, the speech production can be broadly classified into three activities. The first case where the input is nearly periodic in nature, the second case where the input excitation is random noise like in nature and third case where there is no excitation to the system. Accordingly, the speech signal can be broadly classified into three regions. The study of these regions is the aim of this paper. Considering speech signals in short ranges for plotting their waveforms and spectra. The lengths include 10-30 msec. Waveforms and their spectra for segments selected from the word speech recorded using 16 kHz fs (sampling frequency) and 16 bit resolution.
Voiced Speech
If the input excitation to is a system is nearly periodic impulse sequence, then the corresponding speech looks visually nearly periodic and is termed as voiced speech.
Fig 5 Block Diagram of voice speech production
The periodicity associated with the voiced speech can be measured by the autocorrelation analysis. This period is more commonly termed as pitch period. For male: T≈8ms⇒pitch≈125Hz; female: T≈4ms⇒pitch≈250Hz
Unvoiced Speech
If the excitation is random noise-like, then the resulting speech signal will also be random noise-like without any periodic nature and is termed as Unvoiced Speech. The typical nature of excitation and resulting unvoiced speech are shown in figure itself. As it can be seen, the unvoiced speech will be non- periodic in nature. This will be the main difference between voiced and unvoiced speech. The non- periodicity of unvoiced speech can also be observed by the autocorrelation analysis.
Fig 6 Block diagram representation of unvoiced speech production Silence Region
The speech production process consists of generation of voiced and unvoiced speech in succession, separated by silence region. During silence region, there is no excitation supplied to the vocal tract and hence no speech output. However, silence is a part of speech signal. Without the presence of silence region between voiced and unvoiced speech, the speech will not be complete. The duration of silence along with other voiced or unvoiced speech is an indicator of certain types of sounds. Even though from amplitude/energy point of view, silence region is unimportant, but its duration is very essential for intelligible speech.
If the speech signal waveform looks periodic in nature, then it may be marked as voiced speech, otherwise, as unvoiced/silence region based on the associated energy. If the signal amplitude is low or negligible, then it can be marked as silence, otherwise as unvoiced region.
Noise Cancellation
A Prior to processing, the analogue signal must be transformed into the digital form. The procedure of transforming the analogue speech signal into a digital one creates additional noise during sampling, called quantization noise. However, already at the sampling frequency of 8 kHz and 16-bit sample resolution, the intensity of quantization noise is neglectable in comparison to other noise sources (microphone amplifier noise, environmental noise). Once the analogue audio signal is transformed into a digital one, different techniques for noise cancellation and increasing speech signal quality are applied. The basic technique is linear filtering of the digital signal. Linear filtering encompasses signal processing in a time domain, reflected in a change of source signal spectrum content. The goal of filtering is to reduce unwanted noise components from the speech signal. Usually, linear digital filters consist of two types:
1. Finite Impulse Response filters – FIR filters
2. Infinite Impulse Response filters – IIR filters. In FIR filters, the output signal y[t] of a certain linear digital system is determined by convoluting input signal x[t] with impulse response h[t]
Y [ t ] = x [ t] * h [ t ]
Where, t is the time domain value. Along with the time domain, digital filtering can also be conducted in the frequency domain. Digital filters in the frequency domain are divided into four main categories: low-pass, band-pass, band-stop and high-pass.
Noise cancellation using Adaptive Filters
Adaptive Noise Canceller (ANC) removes or suppresses noise from a signal using adaptive filters that automatically adjust their parameters. The ANC uses a reference input derived from single or multiple sensors located at points in the noise field where the signal is weak or undetectable. Adaptive filters then determine the input signal and decrease the noise level in the system output. The parameters of the adaptive filter can be adjusted automatically and require almost neither prior signal information nor noise characteristics. However, the computational requirements of adaptive filters are very high due to long impulse responses, especially during implementation on digital signal processors. Convergence becomes very slow if the adaptive filter receives a signal with high spectral dynamic range such as in non-stationary environments and colored background noise. In the last few decades, numerous approaches have been proposed to overcome these issues.
For example, the Wiener filter, Recursive-Least-Square (RLS) algorithm, and the Kalman filter were proposed to achieve the best performance of adaptive filters. Apart from these algorithms, the Least Mean Square (LMS) algorithm is most commonly used because of its robustness and simplicity. However, the LMS suffers from significant performance degradation with colored interference signals. Other algorithms, such as the Affine Projection algorithm (APA), became alternative approaches to track changes in background noise; but its computational complexity increases with the projection order, limiting its use in acoustical environments.
An adaptive filtering system derived from the LMS algorithm, called Adaptive Line Enhancer (ALE), was proposed as a solution to the problems stated above. ALE is an adaptive self-tuning filter capable of, separating the periodic and stochastic components in a signal. The ALE detects extremely low-level sine waves in noise, and may be applied in speech with noisy environment. Furthermore, unlike ANCs, ALEs do not require direct access to the noise nor a way of isolating noise from the useful signal. In literature, several ALE methods have been proposed for acoustics applications. These methods mainly focus on improving the convergence rate of the adaptive algorithms using modified filter designs, realized as transversal Finite Impulse Response (FIR), recursive Infinite Impulse Response (IIR), lattice, and sub-band filters.
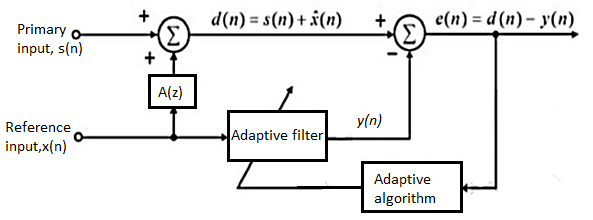
Fig 7 Block diagram of adaptive noise cancellation system
It is shown that for this application of adaptive noise cancellation, large filter lengths are required to account for a highly reverberant recording environment and that there is a direct relation between filter mis-adjustment and induced echo in the output speech. The second reference noise signal is adaptively filtered using the least mean squares, LMS, and the lattice gradient algorithms. These two approaches are compared in terms of degree of noise power reduction, algorithm convergence time, and degree of speech enhancement.
The effectiveness of noise suppression depends directly on the ability of the filter to estimate the transfer function relating the primary and reference noise channels. A study of the filter length required to achieve a desired noise reduction level in a hard-walled room is presented. Results demonstrating noise reduction in excess 10dB in an environment with 0dB signal noise ratio.
Smoothing Algorithm
In many experiments in physical science, the true signal amplitudes (y-axis values) change rather smoothly as a function of the x-axis values, whereas many kinds of noise are seen as rapid, random changes in amplitude from point to point within the signal. In the latter situation it may be useful in some cases to attempt to reduce the noise by a process called smoothing. In smoothing, the data points of a signal are modified so that individual points that are higher than the immediately adjacent points (presumably because of noise) are reduced, and points that are lower than the adjacent points are increased. This naturally leads to a smoother signal. As long as the true underlying signal is actually smooth, then the true signal will not be much distorted by smoothing, but the noise will be reduced.
Most smoothing algorithms are based on the "shift and multiply" technique, in which a group of adjacent points in the original data are multiplied point-by-point by a set of numbers (coefficients) that defines the smooth shape, the products are added up to become one point of smoothed data, then the set of coefficients is shifted one point down the original data and the process is repeated. The simplest smoothing algorithm is the rectangular or unweighted sliding-average smooth; it simply replaces each point in the signal with the average of m adjacent points, where m is a positive integer called the smooth width. For example, for a 3-point smooth (m=3).
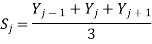
For j = 2 to n-1, where Sj the jth point in the smoothed signal, Yj the jth point in the original signal, and n is the total number of points in the signal. Similar smooth operations can be constructed for any desired smooth width, m.
Usually, m is an odd number. If the noise in the data is "white noise" (that is, evenly distributed over all frequencies) and its standard deviation is s, then the standard deviation of the noise remaining in the signal after the first pass of an unweighted sliding-average smooth will be approximately s over the square root of m (s/sqrt(m)), where m is the smooth width. The triangular smooth is like the rectangular smooth, above, except that it implements a weighted smoothing function. For a 5-point smooth (m = 5)
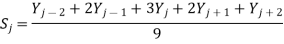
For j = 3 to n-2, and similarly for other smooth widths. It is often useful to apply a smoothing operation more than once, that is, to smooth an already smoothed signal, in order to build longer and more complicated smooths. For example, the 5-point triangular smooth above is equivalent to two passes of a 3-point rectangular smooth. Three passes of a 3-point rectangular smooth result in a 7-point "pseudo-Gaussian" or haystack smooth.
Noise reduction
Smoothing usually reduces the noise in a signal. If the noise is "white" (that is, evenly distributed over all frequencies) and its standard deviation is s, then the standard deviation of the noise remaining in the signal after one pass of a triangular smooth will be approximately s*0.8/sqrt(m), where m is the smooth width. Smoothing operations can be applied more than once: that is, a previously-smoothed signal can be smoothed again. In some cases, this can be useful if there is a great deal of high-frequency noise in the signal. However, the noise reduction for white noise is less in each successive smooth. For example, three passes of a rectangular smooth reduce white noise by a factor of approximately s*0.7/sqrt(m), only a slight improvement over two passes. The frequency distribution of noise, designated by noise color, substantially effects the ability of smoothing to reduce noise.
Key takeaway
Sound is variations in air pressure. The creation of sound is the process of setting the air in rapid vibration. Speech signal is an acoustic signal produced from a speech production system. The system characteristics depend on the design of the system. For the case of LTI system, this is completely characterized in terms its impulse response. However, the nature of output depends on the type of input excitation to the system.
The electrocardiogram (ECG) is used to monitor the proper functioning of heart. The electric signals from the muscle fibres are changed due to stimulation of muscle alters. Cardiac cells, unlike other cells, have a property known as automaticity, which is the capacity to spontaneously initiate impulses. These are then transmitted from cell to cell by gap junctions that connect cardiac cells to each other. The electrical impulses spread through the muscle cells because of changes in ions between intracellular and extracellular fluid. This is referred to as action potential. The primary ions involved are potassium, sodium and calcium. The action potential is the potential for action created by the balance between electrical charges (positive and negative) of ions on either side of the cell membrane. When the cells are in a resting state, the insides are negatively charged compared to the outsides.
Membrane pumps act to maintain this electrical polarity (negative charge) of the cardiac cells. Contraction of the heart muscle is triggered by depolarisation, which causes the internal negative charge to be lost transiently. These waves of depolarisation and repolarisation represent an electrical current and can be detected by placing electrodes on the surface of the body. After the current has spread from the heart through the body, the changes are picked up by the ECG machine and the activity is recorded on previously sensitised paper. The ECG is therefore a graphic representation of the electrical activity in the heart. The current is transmitted across the ECG machine at the selected points of contact of the electrode with the body.
Heart rate variability (HRV) is the physiological phenomenon of variation in heart beats. Even in resting states, spontaneous fluctuations of the intervals between two successive heart beats occur. Spectral analysis of HRV is a non-invasive and easy-to-perform tool for evaluating cardiac autonomic activity. Two critical frequency domain parameters obtained from spectral analysis are widely used: low frequency (LF) power (0.04–0.15 Hz) represents both sympathetic and vagal influences; high frequency (HF) power (0.15–0.40 Hz) reflects the modulation of vagal tone. In addition, LF/HF ratio indicates the balance between sympathetic and vagal tones. Before spectral analysis, we need to carefully inspect the ECG to identify potential artifacts, ectopic beats, and arrhythmic events. Since HRV analysis is based on the sinus rhythm, if left untreated, these artifacts and non-sinus events would introduce errors. For short-term HRV analysis, if possible, recordings that are free of artifacts, ectopic beats, and arrhythmia should be chosen. If the selected data include technical artifacts, such as missed beats (caused by failure to detect the R peak) and electrical noise, we can edit the data by a proper interpolation based on the neighboring RR intervals.
For fast Fourier transform, to satisfy the requirement of equal distance, interpolation is needed. Most commonly, power spectral analysis of HRV is analyzed through fast Fourier transform and autoregressive models, by commercial devices or non-commercial software. In most cases, both methods obtain comparable results, but we need to notice their differences.
The algorithm of fast Fourier transform is relatively simple and has low computational cost. However, fast Fourier transform based spectral analysis is subjected to the problem of non-equal distance of RR intervals and a requirement of stationary data segments. In addition, the length of data segments influences the basic oscillation and the frequency resolution of fast Fourier transform analysis. Therefore, fast Fourier transform based HRV analysis needs artificial interpolation to satisfy the demand on equal distance, but the interpolation would introduce biases. Typically, it works on a stable ECG segment of at least 5 min, this restriction on length sometimes limits its application.
These techniques can obtain instant power spectral profiles of HRV during highly dynamic processes. Spectral analysis of HRV using longer time windows (usually from 1–24 h) has been reported, mainly using fast Fourier transform or autoregressive method. Long-term spectral analysis of HRV has been used in determining the autonomic function, assessing its changes, and predicting prognosis. Shorter and longer time windows have their own advantages and disadvantages according to the particular application scenarios. In the following sections, we will discuss the characteristics of short-term and long-term HRV analysis. In addition, we will also introduce our newly developed long-term MTRS analysis.
Fast Fourier transform and autoregressive based HRV analyses conventionally work on ECG recordings of 2–5 min. As mentioned earlier, short-term MTRS analysis mainly works on 1–2 min. The short-term HRV analysis is often the basis for longer time windows. The most common strategy for long-term HRV analysis is to divide the target time window (e.g., 1 or 24 h) into consecutive 1–5 min epochs, and averaging the individual values of HRV parameters of all these epochs to obtain the mean value of the target time window. MTRS has been traditionally used in short-term HRV analysis, but recently we have developed a newer version of MTRS, which also used the averaging strategy. For a target ECG segment of 30 min to 24 h, this target ECG segment is firstly divided into consecutive 1–2 min global data segments.
Illustrates the strategy by showing how a given 30 min ECG recording is divided into 15 2-min global data segments. Each 2-min global segment was analysed as our traditional short-term MTRS analysis, and then the results of all these 2-min global data segments are averaged to obtain the mean value of the whole targeted 30-min segment. This strategy can be applied even in longer time windows including 24 h. Figure A shows the LF and HF values of the 30 2-min global segments within an hour in a patient with multiple sclerosis, these 2-min values will be averaged to obtain the targeted 1-h results. Figure B shows an application of this long-term MTRS analysis in a patient with multiple sclerosis, who had taken 0.5 mg fingolimod. This figure shows the mean 1 h LF and HF powers of the 6 h after fingolimod intake. This dividing and averaging process is a common strategy for long-term spectral analysis of HRV, and the underlying algorithm can be fast Fourier transform, autoregressive method, or MTRS, etc.
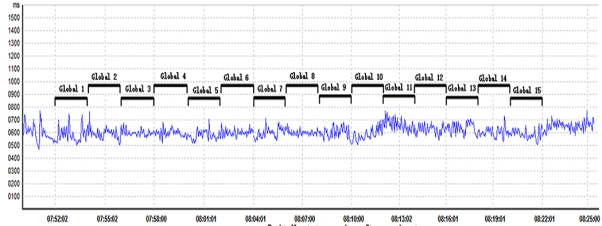
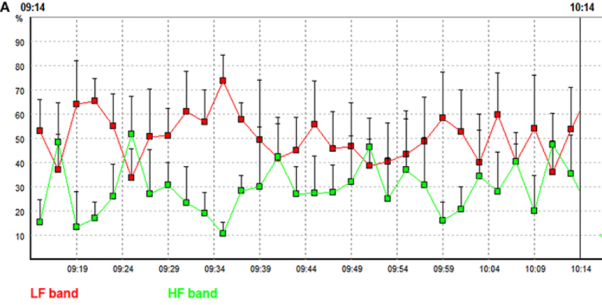

The cardiovascular system is a spatially and temporally complex system. It is built from a dynamic web of interconnected feedback loops. Heart rate, blood pressure, and HRV parameters keep fluctuating constantly, both in the resting state and under various internal and external stimulations. We can estimate HRV parameters in the resting state, during standing and daily activities, in different stages of sleep, and their responses to medications. Choosing the most appropriate time window for HRV analysis can optimize its application.
Key takeaway
For fast Fourier transform, to satisfy the requirement of equal distance, interpolation is needed. Most commonly, power spectral analysis of HRV is analysed through fast Fourier transform and autoregressive models, by commercial devices or non-commercial software. In most cases, both methods obtain comparable results, but we need to notice their differences
Artifacts (noise) are the unwanted signals that are merged with ECG signal and sometimes create obstacles for the physicians from making a true diagnosis. Hence, it is necessary to remove them from ECG signals using proper signal processing methods. There are mainly four types of artifacts encountered in ECG signals: baseline wander, powerline interference, EMG noise and electrode motion artifacts.
Baseline Wander
Baseline wander or baseline drift is the effect where the base axis (x-axis) of a signal appears to ‘wander’ or move up and down rather than be straight. This causes the entire signal to shift from its normal base. In ECG signal, the baseline wander is caused due to improper electrodes (electrode-skin impedance), patient’s movement and breathing (respiration). Figure shows a typical ECG signal affected by baseline wander. The frequency content of the baseline wander is in the range of 0.5 Hz. However, increased movement of the body during exercise or stress test increase the frequency content of baseline wander. Since the baseline signal is a low frequency signal therefore Finite Impulse Response (FIR) high-pass zero phase forward-backward filtering with a cut-off frequency of 0.5 Hz to estimate and remove the baseline in the ECG signal can be used.
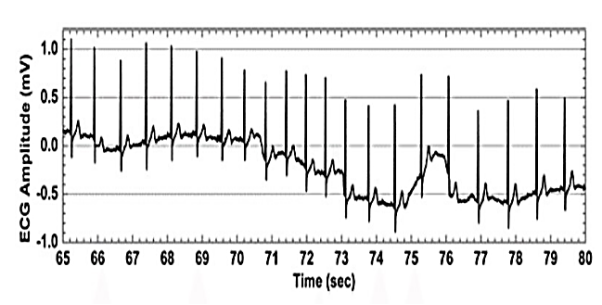
Fig 8 ECG Signal with baseline wander
Powerline Interference
Electromagnetic fields caused by a powerline represent a common noise source in the ECG, as well as to any other bioelectrical signal recorded from the body surface. Such noise is characterized by 50 or 60 Hz sinusoidal interference, possibly accompanied by a number of harmonics. Such narrowband noise renders the analysis and interpretation of the ECG more difficult, since the delineation of low-amplitude waveforms becomes unreliable and spurious waveforms may be introduced. It is necessary to remove powerline interference from ECG signals as it completely superimposes the low frequency ECG waves like P wave and T wave.
EMG Noise
The presence of muscle noise represents a major problem in many ECG applications, especially in recordings acquired during exercise, since low amplitude waveforms may become completely obscured. Muscle noise is, in contrast to baseline wander and 50/60 Hz interference, not removed by narrowband filtering, but presents a much more difficult filtering problem since the spectral content of muscle activity considerably overlaps that of the PQRST complex. Since the ECG is a repetitive signal, techniques can be used to reduce muscle noise in a way similar to the processing of evoked potentials. Successful noise reduction by ensemble averaging is, however, restricted to one particular QRS morphology at a time and requires that several beats be available. Hence, there is still a need to develop signal processing techniques which can reduce the influence of muscle noise [4]. Figure below shows an ECG signal interfered by an EMG noise.
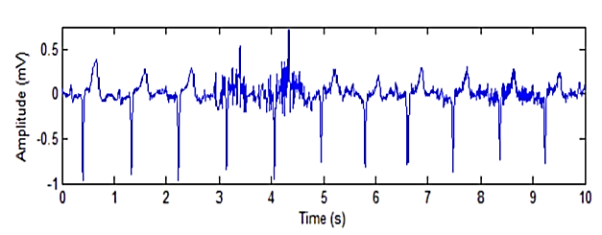
Fig 9 ECG signal with electromyographic (EMG) noise
Electrode Motion Artifacts
Electrode motion artifacts are mainly caused by skin stretching which alters the impedance of the skin around the electrode. Motion artifacts resemble the signal characteristics of baseline wander, but are more problematic to combat since their spectral content considerably overlaps that of the PQRST complex. They occur mainly in the range from 1 to 10 Hz. In the ECG, these artifacts are manifested as large-amplitude waveforms which are sometimes mistaken for QRS complexes. Electrode motion artifacts are particularly troublesome in the context of ambulatory ECG monitoring where they constitute the main source of falsely detected heartbeats.
Techniques for Removal of Baseline Wander
A straightforward approach to the design of a filter is to choose the ideal high-pass filter as a starting
Point. 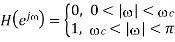
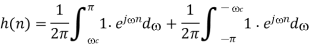
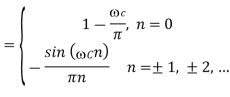
Since the corresponding impulse response has an infinite length, truncation can be done by multiplying h(n) by a rectangular window function, defined by or by another window function if more appropriate. Such an FIR filter should have an order 2L + 1.
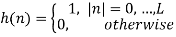
Wavelet transform can also be used to remove the baseline wander from ECG signal. The frequency of baseline wander is approximately 0.5 Hz. According to discrete wavelet transform (DWT), the original signal is to be decomposed using the subsequent low-pass filters (LPF) and high-pass filters (HPF). The cut-off frequency for LPF and HPF will be half of the sampling frequency.
Techniques for Removal of Powerline Interference
A very simple approach to the reduction of powerline interference is to consider a filter defined by a complex conjugated pair of zeros that lie on the unit circle at the interfering frequency.
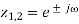
Such a second-order FIR filter has the transfer function
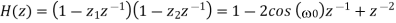
Since this filter has a notch with a relatively large bandwidth, it will attenuate not only the powerline frequency but also the ECG waveforms with frequencies close to ω0. It is, therefore, necessary to modify the filter so that the notch becomes more selective, for example, by introducing a pair of complex conjugated poles positioned at the same angle as the zeros, but at a radius r
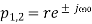
Where 0 <1< r. Thus, the transfer function of the resulting IIR filter is given by
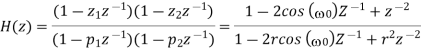
The notch bandwidth is determined by the pole radius r and is reduced as r approaches the unit circle. The impulse response and the magnitude function for two different values of the radius, r = 0.75 and 0.95. From Figure 8 it is obvious that the bandwidth decreases at the expense of increased transient response time of the filter. The practical implication of this observation is that a transient present in the signal causes a ringing artifact in the output signal. For causal filtering, such filter ringing will occur after the transient, thus mimicking the low-amplitude cardiac activity that sometimes occurs in the terminal part of the QRS complex, i.e., late potentials.
Techniques for Removal of Electromyographic (EMG) Noise
The EMG noise is a high-frequency noise; hence an n-point moving average (MA) filter may be used to remove, or at least suppress, the EMG noise from ECG signals. The general form of an MA filter is
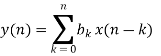
Where x and y are the input and output of the filter, respectively. The bk values are the filter coefficients or tap weights, k = 0, 1, 2, . . . , N, where N is the order of the filter. The effect of division by the number of samples used (N + 1) is included in the values of the filter coefficients.
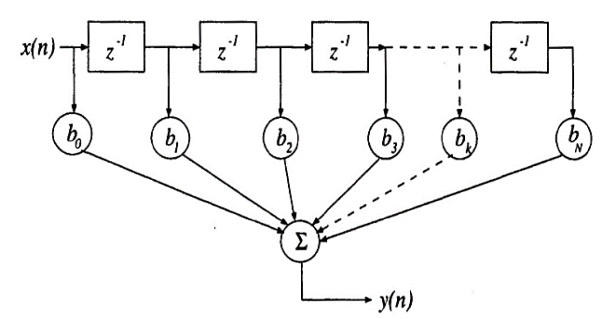
Fig 10 SFG of moving average filter of order N
Increased smoothing may be achieved by averaging signal samples over longer time windows, at the expense of increased filter delay. If the signal samples over a window of eight samples are averaged, we get the output as
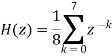
The transfer function of filter becomes
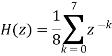
The 8-point MA filter can be written as
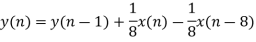
The recursive form as above clearly depicts the integration aspect of the filter. The transfer function of this expression is easily derived to be
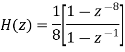
Techniques for Removal of Electrode Motion Artifacts
One of the widely used techniques for removing the electrode motion artifacts is based on adaptive filters. The general structure of an adaptive filter for noise cancelling utilized in this paper requires two inputs, called the primary and the reference signal. The former is the d(t) = s(t) + n1 (t) where s(t) is an ECG signal and n1(t) is an additive noise. The noise and the signal are assumed to be uncorrelated. The second input is a noise u(t) correlated in some way with n1 (t) but coming from another source. The adaptive filter coefficients wk are updated as new samples of the input signals are acquired. The learning rule for coefficients modification is based on minimization, in the mean square sense, of the error signal e(t) = d(t) − y(t) where y(t) is the output of the adaptive filter. A block diagram of the general structure of noise cancelling adaptive filtering is shown in figure. The two most widely used adaptive filtering algorithms are the Least Mean Square (LMS) and the Recursive Least Square (RLS).

Fig: 11 Block diagram of adaptive filtering scheme
Key takeaway
Artifacts (noise) are the unwanted signals that are merged with ECG signal and sometimes create obstacles for the physicians from making a true diagnosis. Hence, it is necessary to remove them from ECG signals using proper signal processing methods. There are mainly four types of artifacts encountered in ECG signals: baseline wander, powerline interference, EMG noise and electrode motion artifacts.
The most widely used R-peak detection method, proposed by Pan and Tompkins, is the Pan-Tomkins method. It is a threshold-based method with low complexity. Other algorithms of R-peak detection can be classified as pattern recognition, wavelet transform, mathematical morphology, and digital filter. In, a real-time R-peak detector using adaptive thresholding was proposed. This algorithm consisted of pre-processing to initialize R- peak threshold and thresholding to adaptively modify the threshold. It achieved sensitivity and positive predictivity higher than 99.3%. In, a different interference-based method was developed. This method could effectively distinguish R-peaks from high amplitude noises but failed to detect R-peaks when abrupt jump of baseline appeared. Many ambulatory ECG devices are generally limited in power supply and computation. The conventional feature extraction algorithms are, from a computational perspective, very intensive tasks, which are typically executed in mainframe-type computational facilities.
In this study, an adaptive and time-efficient ECG R-peak detection algorithm is proposed. The method takes advantage of wavelet-based multiresolution analysis (WMRA) and adaptive thresholding. WMRA is applied to strengthen ECG signal representation by extracting ECG frequency interval of interest from wide-range frequencies, which contain interference such as baseline drift and motion arti- facts. All the noises produce considerable influence on the following thresholding operation. The adaptive thresholding is designed to exclude false R-peaks in the reconstructed signal by WMRA. The proposed algorithm was tested by the MIT-BIH arrhythmia database (MITDB) and the QT database (QTDB). Both accuracy and time consumption of the algorithm were evaluated. By exploring the time-frequency property of ECG, this study aims to conduct preliminary and tentative research on adaptive and time.
R-Peak Detection Algorithm
The R-peak detection system is described in Figure. The purpose of this study is to develop an algorithm which can effectively identify R-peaks mixed in different noises.
Step 1: WMRA Enhancement.
WMRA enhances signals using wavelet transform to extract both time and frequency domain information. This method is very suitable for ECG processing since ECG is essentially nonstationary with small amplitude (0.01~5 mV) and low frequency (0.05~100 Hz). This method also provides low computational cost. By WMRA, signal below 0.05 Hz and above 100 Hz can be filtered from the raw signal. These intervals are not the ECG frequency bands and contain most types of noises. In addition, according to the Nyquist criterion, subfrequency band presented by each decomposition level is directly related to the sampling frequency fs. Consequently, the ECG signals, sampled at 360 Hz in MITDB and 250 Hz in QTDB, are all decompose up to 8 levels in this study.
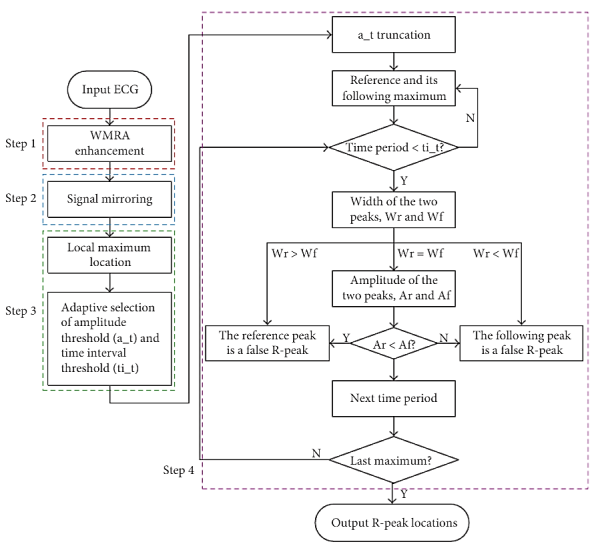
Fig 12 Block Diagram for R algorithm
The decomposition procedure of eight-level WMRA by using bior6.8 wavelet. For MITDB, cD2~cD8consist of frequency components in a range of 0.70–90 Hz, which is the ECG frequency band of interest. CD1with frequency band 90~180 Hz and cA8with frequency band 0~0.70 Hz are beyond the ECG frequency; they are not the considered coefficients containing baseline drift and other interference. Consequently, cD1and cA8are set to zeroes; cD2~cD8are kept for reconstruction. Similarly, for QTDB, cA8with frequency band 0~0.49 Hz is set to zero; cD1~cD8with frequency components in a range of 0.49 -125 Hz are kept. All the retained coefficients are then filtered by the wavelet shrinking threshold algorithm. In this study, soft thresholding is adopted due to its good continuity and no Gibbs phenomenon on step points.
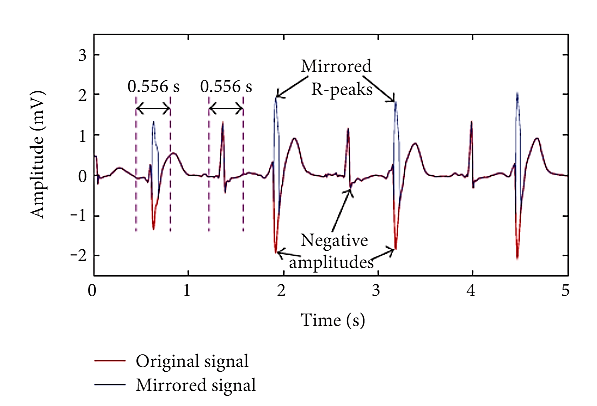

Fig 13 Decomposition process of the eight-level WMRA.
Step 2: Signal Mirroring. For some ECG patterns, such as
Step 2 Signal Mirroring
For some ECG patterns, such as premature ventricular contraction (PVC) beat, R-peaks are presented with amplitude below the baseline but other features are above the baseline. To avoid the potential missing detection, signal mirroring is designed. The mirroring procedure for a PVC segment is described in Figure. Large negative amplitudes are mirrored by taking the baseline as their symmetrical axis. However, not all the negative amplitudes are mirrored, they should be significantly distinctive from adjacent negative values. This assumption is based on the fact that R-peaks have steep slopes while other waves such as P wave and T wave have gentle ones. Steep slope means drastic increment and decrement on both sides of
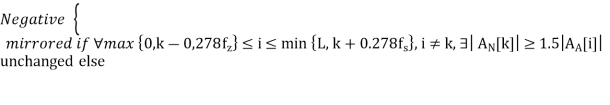
Where Lis the signal length, ANkis the amplitude of large negative point with position number kin signal, 0<k≤L, and AAiis the amplitude of point within 0.278 s before and after the large negative point.
Step 3: Local Maximum Location and Adaptive Threshold Selection.
Local maximums are located by implementing first-order forward differential in the mirrored signal. The Local maximums are located by implementing first-order forward differential in the mirrored signal. The procedure is illustrated as follows
1) First-order forward difference is implemented on ECG signal with ΔECG n= ECG n+1 −ECG n.
(2) For all the elements in ΔECG n, values less than, equal, and more than 0 are replaced by −1, 0, and 1, respectively
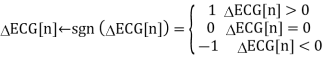
(3) First-order forward difference is implemented on the updated ΔECG n, and the value of ΔECG nis symbolized by −2, 0, and 2. Local maximums in original ECG signal are positions shifted by 1 sample to the right of −2
Step 4: Threshold Recognition. Actually, most of the local
Step 4: Threshold Recognition
Most of the local maximums are not true R-peaks, such as burst points caused by high-frequency interference. The difficulty of R-peak detection lies in the recognition of false R-peaks with amplitudes approximate to or even larger than true R-peaks. To this end, atis designed to filter the local maximums with small amplitudes. In general, there should be no extra R- peaks between two adjacent R-peaks; otherwise, the extra R-peaks are definitely false. Assisted by this knowledge, ti t is designed to further remove false R-peaks omitted by at.

The thresholding algorithm is plotted in Figure. The example ECG is from the Record 200 in MITDB with PVC beats. It comprises of large negative R-peaks, and consequently, the signal needs to be mirrored. The marks Min Figure signify the mirrored R-peaks, where they should originally be large negative amplitudes. After the amplitude filtration, the time interval threshold algorithm is summarized as follows:
(1) Step A. A local maximum and its following maximum are chosen as true reference (Tref) and comparative reference (Cref) respectively, turn to Step B. If there is no Cref,Tref is considered as a true R-peak and the algorithm ends.
(2) Step B. The time period (t_p) between Tref and Cref is calculated. If t_p<ti_t, it indicates that one of the two maximums is a false R-peak, then turn to Step C. Otherwise, Tref is considered as a true R-peak, Cref replaces Tref as true reference, then turn to Step A for next thresholding.
(3) Step C. Widths along the baseline of Tref (Wr) and Cref (Wf) are compared, if Wr<Wf,Tref is considered to be a true R-peak, if Wr>Wf,Cref is treated as a true R-peak. Then turn to Step E. If Wr=Wf, turn to Step D.
(4) Step D. Amplitude of Tref (Ar) and Cref (Af) is com- pared, if Ar>Af,Tref is considered to be a true R- peak, otherwise, Cref is treated as a true R-peak. Then turn to Step E.
(5) Step E. The false maximum is replaced by the third local maximum (Rref) just behind the two maximums, which is treated as a new Cref, and then return to Step B. If there is no Rref in the time period, turn to Step A.
Key takeaway
The most widely used R-peak detection method, proposed by Pan and Tompkins, is the Pan-Tomkins method. It is a threshold-based method with low complexity. Other algorithms of R-peak detection can be classified as pattern recognition, wavelet transform, mathematical morphology, and digital filter. In, a real-time R-peak detector using adaptive thresholding was proposed. This algorithm consisted of pre-processing to initialize R- peak threshold and thresholding to adaptively modify the threshold.
An image is denoted by a two dimensional function of the form f{x, y}. The value or amplitude of ‘f’ at spatial coordinates {x,y} is a positive scalar quantity whose physical meaning is determined by the source of the image. When an image is generated by a physical process, its values are proportional to energy radiated by a physical source. As a consequence, f(x,y) must be nonzero and finite; that is 0 <f(x,y) <∞
The function f(x,y) may be characterized by two components-
· The amount of the source illumination incident on the scene being viewed.
· The amount of the source illumination reflected back by the objects in the scene
These are called illumination and reflectance components and are denoted by i(x,y) and r(x,y) respectively. The functions combine as a product to form f(x,y)
We call the intensity of a monochrome image at any coordinate (x,y) the gray level of the image at that point l= f (x, y) , Lmin ≤ l ≤ Lmax
Lmin is to be positive and Lmax must be finite
Lmin = imin rmin
Lmax = imax rmax
The interval [Lmin, Lmax] is called gray scale. Common practice is to shift this interval numerically to the interval [0, L-l] where l=0 is considered black and l= L-1 is considered white on the gray scale. All intermediate values are shades of gray varying from black to white.
Image Digitization
To create a digital image, we need to convert the continuous sensed data into digital from.
This involves two processes – sampling and quantization. An image may be continuous
With respect to the x and y coordinates and also in amplitude. To convert it into digital form we have to sample the function in both coordinates and in amplitudes.
- Digitalizing the coordinate values is called sampling
- Digitalizing the amplitude values is called quantization
There is a continuous image along the line segment AB. To sample this function, we take equally spaced samples along line AB. The location of each sample is given by a vertical tick back (mark) in the bottom part. The samples are shown as block squares superimposed on function the set of these discrete locations gives the sampled function.
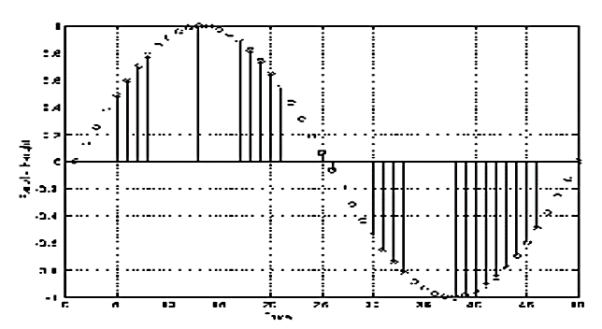
In order to form a digital image, the gray level values must also be converted (quantized) into discrete quantities. So we divide the gray level scale into eight discrete levels ranging from black to white. The vertical tick mark assign the specific value assigned to each of the eight level values.
The continuous gray levels are quantized simply by assigning one of the eight discrete gray levels to each sample. The assignment it made depending on the vertical proximity of a simple to a vertical tick mark.
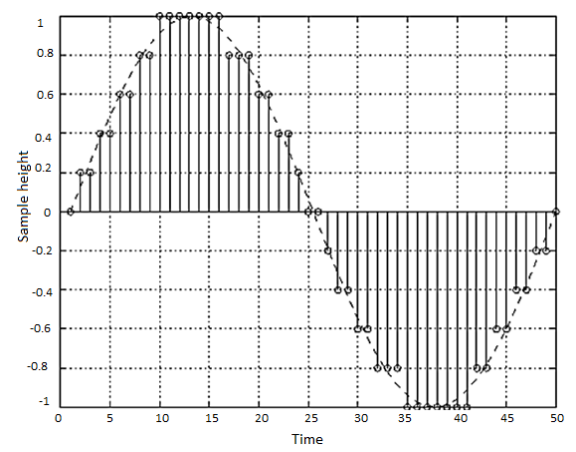
Starting at the top of the image and covering out this procedure line by line produces a two-dimensional digital image.
A digital image f[m,n] described in a 2D discrete space is derived from an analog image f(x,y) in a 2D continuous space through a sampling process that is frequently referred to as digitization. Some basic definitions associated with the digital image are described.
The 2D continuous image f(x,y) is divided into N rows and M columns. The intersection of a row and a column is termed a pixel. The value assigned to the integer coordinates [m,n] with {m=0,1,2,..., M-1}and{n=0,1,2,...,N-1}is f[m, n]. In fact, in most cases f(x,y) is actually a function of many variables including depth (d), color(μ) and time (t).

There are three types of computerized processes in the processing of image
1) Low level process- these involve primitive operations such as image processing to reduce noise, contrast enhancement and image sharpening. This kind of process are characterized by fact the both inputs and output are images.
2) Mid-level image processing - it involves tasks like segmentation, description of those objects to reduce them to a form suitable for computer processing, and classification of individual objects. The inputs to the process are generally images but outputs are attributes extracted from images.
3) High level processing – It involves “making sense” of an ensemble of recognized objects, as in image analysis, and performing the cognitive functions normally associated with vision.
Representing Digital Images
The result of sampling and quantization is matrix of real numbers. Assume that an image f(x,y) is sampled so that the resulting digital image has M rows and N Columns. The values of the coordinates (x,y) now become discrete quantities thus the value of the coordinates at origin become (x,y) =(0,0) The next Coordinates value along the first signify the image along the first row. It does not mean that these are the actual values of physical coordinates when the image was sampled. Thus, the right side of the matrix represents a digital element, pixel or pel. The matrix can be represented in the following form as well.
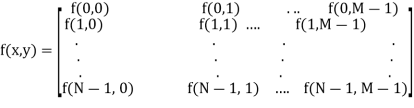
The sampling process may be viewed as partitioning the x-y plane into a grid with the coordinates of the center of each grid being a pair of elements from the Cartesian products Z2 which is the set of all ordered pair of elements (Zi, Zj) with Zi and Zj being integers from Z.
Hence f(x,y) is a digital image if gray level (that is, a real number from the set of real number R) to each distinct pair of coordinates (x,y). This functional assignment is the quantization process. If the gray levels are also integers, Z replaces R, and a digital image become a 2D function whose coordinates and the amplitude value are integers.
Due to processing storage and hardware consideration, the number of gray levels typically is an integer power of 2. L=2K
Then, the number b, of bits required to store a digital image is
B=M *N* K
When M=N The equation become b=N2*K
When an image can have 2k gray levels, it is referred to as “k- bit”. An image with 256 possible gray levels is called an “8-bit image (because 256=28).
Key takeaway
There are three types of computerized processes in the processing of image
1) Low level process- these involve primitive operations such as image processing to reduce noise, contrast enhancement and image sharpening. This kind of process are characterized by fact the both inputs and output are images.
2) Mid-level image processing - it involves tasks like segmentation, description of those objects to reduce them to a form suitable for computer processing, and classification of individual objects. The inputs to the process are generally images but outputs are attributes extracted from images.
3) High level processing – It involves “making sense” of an ensemble of recognized objects, as in image analysis, and performing the cognitive functions normally associated with vision.
Spatial Resolution
There are different definitions of spatial resolution but in a general and practical sense, it can be referred to as the size of each pixel. It is commonly measured in units of distance, i.e. cm or m. In other words, spatial resolution is a measure of the sensor’s ability to capture closely spaced objects on the ground and their discrimination as separate objects. Spatial resolution of a data depends on altitude of the platform used to record the data and sensor parameters. Relationship of spatial resolution with altitude can be understood with the following example. You can compare an astronaut on-board a space shuttle looking at the Earth to what he/she can see from an airplane. The astronaut might see a whole province or country at a single glance but will not Image Resolutions be able to distinguish individual houses. However, he/she will be able to see individual houses or vehicles while flying over a city or town. By comparing these two instances you will have better understanding of the concept of spatial resolution. This can be further elaborated by considering an example shown in Figure below.

Fig 15 Spatial variations of remote sensing data.
Suppose you are looking at a forested hillside from a certain distance. What you see is the presence of the continuous forest; however from a great distance you do not see individual trees. As you go closer, eventually the trees, which may differ in size, shape, and species, become distinct as individuals. As you draw much nearer, you start to see individual leaves (Fig. Below). You can carry this even further, through leaf macro-structure, then recognition of cells, and with further higher spatial resolutions individual constituent atoms and finally subatomic components can be done.

Fig 16 Understanding concept of spatial resolution
The details of features in an image are dependent on the spatial resolution of the sensor and refer to the size of the smallest possible feature that can be detected. Spatial resolution depends primarily on the Instantaneous Field of View (IFOV) (Fig.A) of the sensors which refers to the size of the smallest possible feature that can be detected by each sampling unit of the sensor. Usually, people think of resolution as spatial resolution, i.e. the fineness of the spatial detail visible in an image. The most commonly quoted quantity of the IFOV is the angle subtended by the geometrical projection of single detector element to the Earth’s surface.
Remote sensing instrument is located on a sub-orbital or satellite platform, where è of IFOV, is the angular field of view of the sensor (Fig. Below B). The segment of the ground surface measured within the IFOV is normally a circle of diameter D given by
D = è* H ………………...(1)
Where, D = diameter of the circular ground area viewed
H = flying height above the terrain, and
è = IFOV of the system (expressed in radians).
The ground segment sensed at any instant is called ground resolution element or resolution cell.
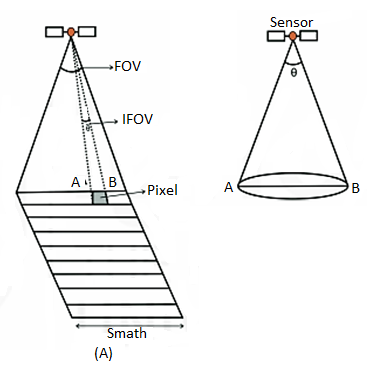
Fig: 17 Schematics showing (A) relationship of IFOV and FOV and (B) concept of IFOV
Spatial resolution of remote sensing system is influenced by the swath width. Spatial resolution and swath width determine the degree of detail that is revealed by the sensors and the area of coverage. Remote sensing sensors are generally categorised into coarse, intermediate and high spatial resolution sensors based on their spatial resolution. Sensors having coarse resolution provide much less detail than the high spatial resolution sensors. Because of the level of details, the sensors provide, they are used for mapping at different scales. High spatial resolution sensors are used for large scale mapping (small area mapping) whereas coarse spatial resolution data are used for regional, national and global scale mapping.
Temporal Resolution
In addition to spatial, spectral and radiometric resolution, it is also important to consider the concept of temporal resolution in a remote sensing system. One of the advantages of remote sensing is its ability to observe a part of the Earth (scene) at regular intervals. The interval at which a given scene can be imaged is called temporal resolution. Temporal resolution is usually expressed in days. For instance, IRS-1A has 22 days temporal resolution, meaning it can acquire image of a particular area in 22 days interval, respectively.
Low temporal resolution refers to infrequent repeat coverage whereas high temporal resolution refers to frequent repeat coverage. Temporal resolution is useful for agricultural application (Fig. Below) or natural disasters like flooding (Fig. Below) when you would like to re-visit the same location within every few days. The requirement of temporal resolution varies with different applications. For example, to monitor agricultural activity, image interval of 10 days would be required, but intervals of one year would be appropriate to monitor urban growth patterns.

Fig 18 Temporal variations of remote sensing data used to monitor changes in agriculture, showing crop conditions in different months

Fig 19 Showing the importance of temporal resolution.
Approximately 0945 h and 1030 h local sun time, respectively. However, this is subject to slight variation due to orbital perturbations. Both satellites pass overhead earlier in the day north of the equator and later to the south. The cross-track width of the imaging strip is an important parameter in deciding temporal resolution.
Key takeaway
Spatial Resolution
There are different definitions of spatial resolution but in a general and practical sense, it can be referred to as the size of each pixel. It is commonly measured in units of distance, i.e. cm or m. In other words, spatial resolution is a measure of the sensor’s ability to capture closely spaced objects on the ground and their discrimination as separate objects
When convolution between two signals which are spanning around mutually perpendicular dimensions is called as 2D convolution. The convolution is similar to 1D convolution where it is done by multiplying and accumulating the instantaneous values of oversampling samples which are corresponding to the two input signals, out of which one is flipped. This can be understood with help of one example.
Let the below matrix x be of the original image and h represent the kernel.
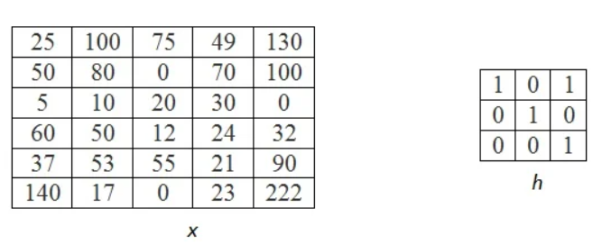
Step 1
In this firstly the rows are converted to columns, and then again rows are flipped along the columns. We can also say that (i,j)th element of original kernel become the (j,i)th element of new matrix.
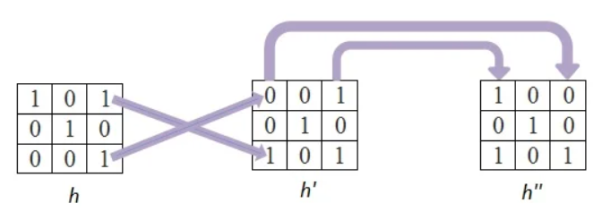
Step 2
Next the inverted kernels are overlapped over the image pixel by pixel. The product of mutually overlapping pixels is calculated and their sums are found. This becomes the value of output pixel for that particular location. Where there is no overlapping pixel, it is assumed to be 0.
The above process is now shown in detail. When pixel of kernel at bottom right falls on first pixel of the image matrix at the top left. The value 25x1 =25 becomes the first pixel value of the output image.
Now the two value of kernel matrix (0,1) in the same row overlap with two pixels of the image (25, 100). The output pixel will be (25x0+100x1) = 100.
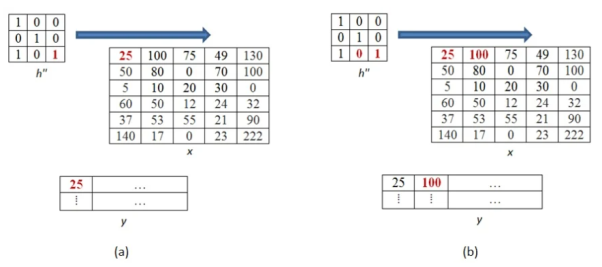
Further continuing same process, we get the values of the output pixels for each pixel. The fourth and seventh output pixel matrix are shown below.
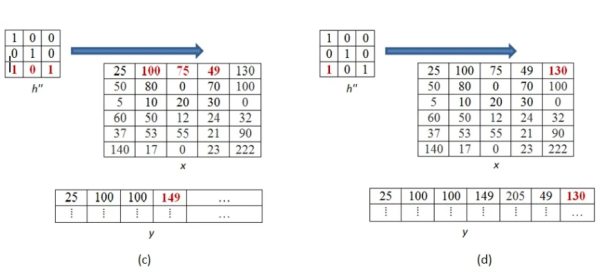
When we move vertically down by a single pixel then the first overlap is shown below. The value of output pixel is obtained by MAC [25x0+50x1] =50. Further we keep moving until we find overlap between all values of kernel and image matrices. For example, the sixth output pixel value will be [49x0 +130x1+70x1+100x0] =200 shown below.
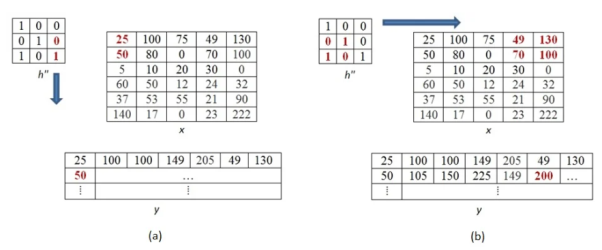
This process of moving one step down followed by horizontal scanning has to be continued until the last row of the image matrix. Three random examples concerned with the pixel outputs at the locations (4,3), (6,5) and (8,6) are shown in Figure below.
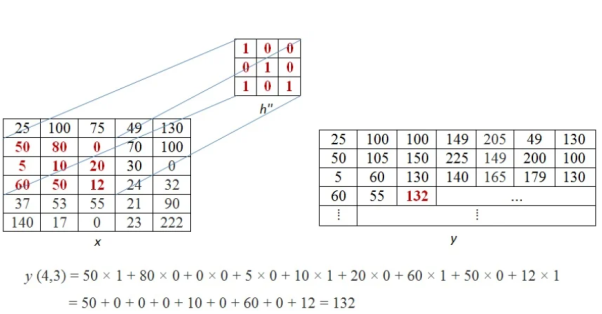
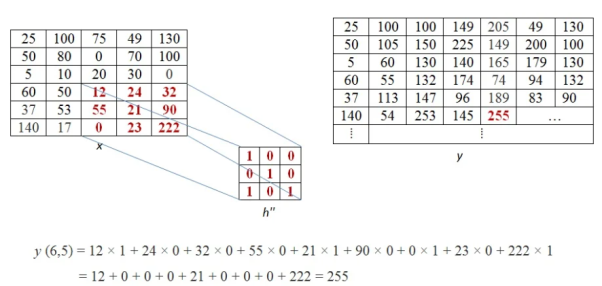
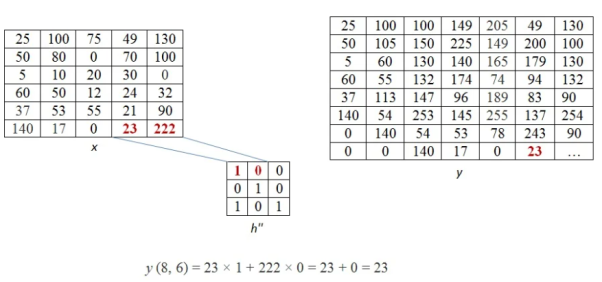
The value of the final output matrix will be
25 | 100 | 100 | 149 | 205 | 49 | 130 |
50 | 105 | 150 | 225 | 149 | 200 | 100 |
5 | 60 | 130 | 140 | 165 | 179 | 130 |
60 | 55 | 132 | 174 | 74 | 94 | 132 |
37 | 113 | 147 | 96 | 189 | 83 | 90 |
140 | 54 | 253 | 145 | 255 | 137 | 254 |
0 | 140 | 54 | 53 | 78 | 243 | 90 |
0 | 0 | 140 | 17 | 0 | 23 | 255 |
Padding Zero
The convolution for 2D is given by
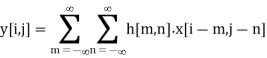
X: input image matrix
H: kernel matrix
Y: Output image
i,j: indices of image matrix
Let us suppose 3x3 kernel convolve then m and n range from -1 to 1. The expansion will now be
y[i,j]= 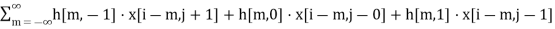
y[i,j]=h[−1,−1]⋅x[i+1,j+1]+h[−1,0]⋅x[i+1,j]+h[−1,1]⋅x[i+1,j−1]+h[0,−1]⋅x[i,j+1]+h[0,0]⋅x[i,j]+h[0,1]⋅x[i,j−1]+h[1,−1]⋅x[i−1,j+1]+h[1,0]⋅x[i−1,j]+h[1,1]⋅x[i−1,j−1]
From above equation we see that in order to find every output pixel nine multiplications are required. The result obtained by the summation of nine product terms can be equal to the product of a single term if the collective effect of the other eight product terms equalizes to zero. One such way is the case in which each product of the other eight terms evaluates, themselves to be zero. In the context of our example, this means, all the product terms corresponding to the non-overlapping (between image and the kernel) pixels must become zero in order to make the results of formula-computation equal to that of graphical-computation.
If at least one of the factors involved in multiplication is zero, then the resulting product is also zero. By this analogy, we can state that, in our example, we need to have a zero-valued image-pixel corresponding to each non-overlapping pixels of the kernel matrix.
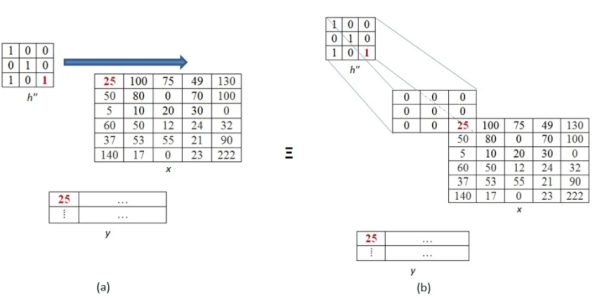
The process of adding zeros is called zero padding. It is done in all the places where the image pixel and kernel pixel do not overlap.
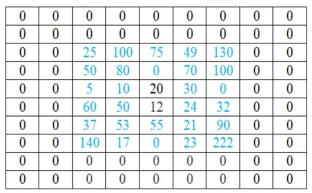
The number of rows or column to be padded with 0 are calculated as number of rows or column in kernel-1.
Key takeaway
The padding of zero is one of the ways to deal with edge effect by convolution. There are many more techniques like replicate padding, mirroring etc.
References:
1. Ifeachor E.C, Jervis B. W, “Digital Signal Processing: Practical approach”, Pearson Publication, 2nd Edition.
2. Li Tan, “Digital Signal Processing: Fundamentals and Applications”, Academic Press, 3rd Edition.
3. Schaum's Outline of “Theory and Problems of Digital Signal Processing”, 2nd Edition.
4. Oppenheim, Schafer, “Discrete-time Signal Processing”, Pearson Education, 1st Edition.
5. K.A. Navas, R. Jayadevan, “Lab Primer through MATLAB”, PHI, Eastern Economy Edition.