Unit-3
Galvanometer
Figure 1. D'Arsonal Galvanometer
The construction of galvanometer consists of
- Moving coil:
It is the current carrying element. It is either rectangular or circular in shape and consists of several turns of fine wire. This coil is suspended so that it is free to tum about its vertical axis of symmetry. It is arranged in uniform, radial, horizontal magnetic field in the air gap between pole pieces and armature (iron core) of a permanent magnet. The armature (iron core) is spherical in shape if the coil is circular but is cylindrical if the coil is rectangular.
2. Damping
There is a damping torque present owing to production of eddy currents in the metal former on which the coil is mounted. Damping is also obtained by connecting a low resistance across the galvanometer terminals.
3. Suspension
The coil is supported by a fiat ribbon suspension which also carries current to the coil. The other current connection in a sensitive galvanometer is a coiled wire. This is called the lower suspension and has a negligible torque effect. This type of galvanometer must be levelled carefully so that the coil hangs straight and centrally without rubbing the poles or the soft iron cylinder.
4. Indication.
The suspension carries a small mirror upon which a beam of light is cast. The beam of light is reflected on to a scale upon which the deflection is measured. This scale is usually about 1 metre away from the instrument, although 1 /2 metre may be used for greater compactness.
3.1.2 Theory and Principle of Operation of Galvanometer
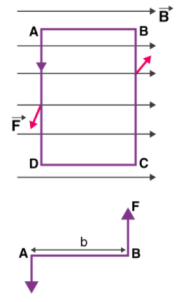
Initially consider a single turn ABCD of the rectangular coil having a length l and breadth b. This is suspended in a magnetic field of strength B such that the plane of the coil is parallel to the magnetic field.
Since the sides AB and DC are parallel to the direction of the magnetic field, they do not experience any effective force due to the magnetic field. The sides AD and BC being perpendicular to the direction of field experience an effective force F given by F=BI.l
|
Figure 2. Current carrying loop in magnetic field.
We know that torque τ = force x perpendicular distance between the forces
τ = F × b
Substituting the value of F, we already know,
Torque τ acting on single-loop ABCD of the coil = BI l × b
Where lx b is the area A of the coil,
Hence the torque acting on n turns of the coil is given by
τ = n IAB
The magnetic torque thus produced causes the coil to rotate, and the phosphor bronze strip twists. In turn, the spring S attached to the coil produces a counter torque or restoring torque k θ which results in a steady angular deflection.
Under equilibrium condition:
K θ = n IAB
Here k is called the torsional constant of the spring (restoring couple per unit twist). The deflection or twist θ is measured as the value indicated on a scale by a pointer which is connected to the suspension wire.
θ= (nAB / k) I
Therefore θ ∝ I
Key Takeaways:
It is one of the common measuring instruments. The galvanometer is used for detecting the presence of small voltages or currents to indicate zero current in applications like bridge circuit.
|
Figure 3. Vibration Galvanometer
The figure shows the construction of Duddell’s Moving coil galvanometer. The moving coil consists of fine bronze or platinum silver wire. This wire passes over small pulley at top and is pulled tight by a spring attached to the pulley, the tension of the spring can be adjusted by turning a milled head attached to the spring.
The loop of wire is stretched over two ivory bridge pieces the distance between these pieces is adjustable. When the moving coil vibrates due to passage of a.c the reflected beam from the mirror throws a band of light upon a scale provided for this purpose.
Tuning: Tuning means adjustment of the natural frequency of the moving system so that it is equal to the frequency of the current passing through the coil.
Tuning is done by varying the distance between the bridge pieces. This varies the length of the loop which is free to vibrate and thus varies the natural frequency of the moving system. Fine adjustment is done by varying the tension of the spring.
When the galvanometer is tuned the amplitude of vibrations is very large and consequently a very wide band of light is observed on the scale.
Let the value of current passing through the moving coil at an instant t be
i = Im sin wt
Deflecting torque Ta = Gi = G Im sin wt
Equation of motion is Ti + TD + Tc = Td
J . d 2  / dt 2 + D d
/ dt 2 + D d / dt + K
/ dt + K  = G Im sin wt
= G Im sin wt
A = l × b When current flows across the coil, then the torque is developed. The magnitude of the torque is given by τ = Ni B A Assume that the flow of current across the coil for each minimal time is dt and so the change in current is represented as τ dt = Ni BA dt When there is current flow across the coil for a time of ‘t’ seconds, then the value is represented as ʃ0t τ dt = NBA ʃ0t idt = N B Aq where ‘q’ is the total amount of charge that flows across the coil. The inertial moment that exists for the coil is shown as ‘I’ and the coil’s angular velocity is shown as ‘ω’. The below expression provides the angular momentum of the coil and it is lω. It is like the pressure that is applied to the coil. By multiplying the above two equations, we get lw = NB Aq Also, the kinetic energy across the coil will have deflection at ‘ϴ’ angle and the deflection will be restored using the spring. It is represented by Restoring torque value = (1/2)cϴ2 Kinetic energy value = (1/2)lw2 As the coil’s restoring torque is similar to the deflection then (1/2)cϴ2 = (1/2)lw2 cϴ2 = lw2 Also, the periodic oscillations of the coil is shown as below T = 2π√(l/c) T2 = (4π2l/c) (T2/4π2) = (l/c) (cT2/4π2) = l Finally, (ctϴ/2π) =lw = NBAq q = (ctϴ)/NBA2π q = [(ct)/NBA2π] * ϴ) Assume that k = [(ct)/NBA2π Then q = k ϴ So, ‘k’ is the constant term of the ballistic galvanometer. |
Key Takeaway:
The galvanometer which is used for estimating the quantity of charge flow through it is called the ballistic galvanometer
References
- Elements of Electronic Instrumentation and Measurement – by Carr
- Basic Electrical, Electronics and Measurement Engineering Paperback – 1 January 2019 by U.A Bakshi and A.P Godse.
- Electrical and Electronic Measurement and Instrument Paperback R.K Rajput
- Electrical & Electronic Measurements B. P. Patil, Pooja Mogre (Bisen)
- Electronic Measurements and Instrumentation by A.K. Sawhney