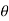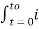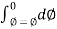Unit-6
Magnetic Measurements
6.1.1 Measurement of magnetic flux by ballistic galvanometer
|
Figure 1. Ballistic Galvanometer
To measure the magnetic flux of a bar magnet, the bar magnet is surrounded by a coil connected in series with a variable resistor and galvanometer. The series resistor provides critical damping and used to control the sensitivity of the magnetic flux. This sensitivity is controlled by adjusting the number of turns in a coil.
When the magnet is suddenly withdrawn from the coil, an impulse is produced in a coil for few seconds and the deflection of the galvanometer is taken as measure of the flux. The induced voltage in the coil are:
e = N dɸ/dt volts ------------------------------------------------------(1)
where flux is measured in Weber’s and N is the number of turns in a coil. If R is the total resistance of the circuit including series resistor and a galvanometer then the current flowing to the circuit is:
i= e/R = N/R x d
or |
|
The quantity of charge passed through the galvanometer is:
Q = N ɸ/R coulombs ---------------------------------------------------------(3)
Deflection of the galvanometer is:
Or
ɸ= K2 R
Where K2 is the sensitivity factor. |
6.1.2 Measurement of magnetic flux by fluxmeter
A Fluxmeter is an electronic integrating, digital display instrument. The Fluxmeter can be used not only for the measurement of the magnetic flux of permanent magnets, but also for quality control and sorting of magnetic products.
Most Fluxmeters have the functions such as maximum value hold and automatic pole indication and different measuring ranges. They can be used also for measurement of impulse magnetic field.
Key Takeaways:
Ballistic galvanometers are the measuring instruments which are used for measuring the quantity of electric charges obtained from magnetic flux.
|
Figure 2. Measurement of magnetic flux B-H curve
A ring- shaped specimen with known dimensions are used for this purpose.
After demagnetizing the test is started by setting the magnetising current to its lowest test value. With galvanometer key K closed, the iron specimen is brought into a ‘reproducible cyclic magnetic state’ by throwing the reversing switch S backward and forward about twenty times.
Key K is now opened and the value of flux corresponding to this value of H which is measured by reversing the switch S and noting the throw of galvanometer .The value of flux density corresponding to H can be calculated by dividing the flux by the area of the specimen.
The above procedure is repeated for various values of H up to the maximum testing point. The B-H curve may be plotted from the measured values of B corresponding to the various values of H.
Determination of Hysteresis Loop
Method of reversals
This test is done by means of number of steps, but the change in flux density measured at each step is the change from the maximum value + Bm down to some lower value.
But before the next step is commenced the iron specimen is passed through the remainder of the cycle of magnetization back to the flux density + Bm. Thus, the cyclic state of magnetization is preserved.
The connections for the method of reversals are shown in Fig.
|
Figure 3. Magnetic flux by hysteresis loop
Key Takeaways:
A hysteresis loop shows the relationship between the induced magnetic flux density (B) and the magnetizing force (H). It is often referred to as the B-H loop.
When a transformer is operated at no load the power drawn from the supply is equal to the no load losses which are equal to the sum of constant losses and copper losses in primary winding. The no load current of the transformer is quite small, and the resistance of the primary winding is also low such as copper losses in primary winding. Hence, the power drawn from the supply under no load condition can be approximately taken as total iron losses.
Iron losses = Hysteresis loss + Eddy current loss
Hysteresis loss α B n f α f with flux density being kept constant = K1f
Eddy current loss α B2 f2 α f2 with flux density being kept constant = K2 f2
Where K1 and K2 are constants for transformer.
Key Takeaway:
In order to estimate the iron loss generated by distorted fluxes accurately, the hysteresis and eddy current loss curves are needed.
Lloyd Fisher square is the most used magnetic square. The strips are usually 0.25m long and 50 to 60mm wide. Each stack is made up of two types of strips one in the direction of rolling and the other cut perpendicular to the direction of rolling. The individual strips are insulated from each other. These strips are built up into four stacks and assembled to form complete magnetic circuit with the help of bent corner pieces and clamps. These corner pieces should be of the same material as the strips or at least material having similar magnetic properties. The bundle of strips are placed inside four similar magnetizing coils of heavy wire connected in series to form primary winding. Each of these coils has underneath it two single layer coils of thin wire having equal no of turns . These secondary coils are connected in series in groups of four-one each core to form two separate and similar secondary windings.
The supply frequency is adjusted to the correct value and the magnetizing current is adjusted to give the required value of Bmax and readings of wattmeter and voltmeter are noted.
The electrostatic voltmeter connected across S2 measures the rms value of induced voltage. The value of the induced voltage is
E = 4KfB’maxAfN2 volts
Where Kf-form factor
Bmax max flux density
A -> cross sectional area of specimen
f-> supply frequency in Hz
N2-> no of turns of secondary winding S2
The cross section of the coil Ac is larger than As. Thus, S2 encloses flux in the air space between specimen and coil addition to the flux in the specimen. Correction needs to be applied for the value of Bmax. Thus, the actual value of flux density in the specimen is
Bm = B’max – μoHmax(Ac/As -1) where Hm-> maximum magnetizing force.
Key Takeaways:
Iron loss measurement methods are presented, where the losses are determined by magnetic material investigations and electrical power measurements.
References:
- Elements of Electronic Instrumentation and Measurement – by Carr
- Basic Electrical, Electronics and Measurement Engineering Paperback – 1 January 2019 by U.A Bakshi and A.P Godse.
- Electrical and Electronic Measurement and Instrument Paperback R.K Rajput
- Electrical & Electronic Measurements B. P. Patil, Pooja Mogre (Bisen)
- Electronic Measurements and Instrumentation by A.K. Sawhney