Unit 3

Content:

3.1 Joint Distributions

A joint distribution is a probability distribution having two or more independent random variables. In joint distribution, each random variable has its own probability distribution, expected value, variance, and standard deviation. Also probabilities exist for ordered pair values of the random variables.

Most often, a joint distribution having two discrete random variables is given in table form. In this situation, the body of the table contains the probabilities for the different ordered pairs of the random variables, while the margins contain the probabilities for the individual random variables.

Suppose a joint distribution of the random variables X and Y are given in table form, so that   PXY(X=x,Y=y) typically abbreviated as   PXY(x,y) is given for each pair   (x,y),   of random variables.

3.2 Function of one or two variables

As with all discrete distributions, two requirements must hold for each pair  (x,y)

0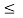PXY(x,y) 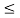1

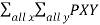(x,y) =1

Then the marginal probabilities PX(X=x) and PY(Y=y), the expected values E(X) and E(Y), and the variances Var(X) and Var(Y) can be found by the following formulas

PX(X=x) = 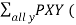x,y)

PY(Y=x) = 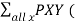x,y)

E(X) =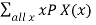

E(Y) =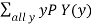

Var(X) = 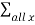x 2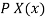 – (E(X)) 2

Var(Y) = y 2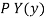 – (E(Y)) 2

To measure any relationship between two random variables, we use the covariance, defined by the following formula.

Cov (X,Y) = 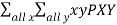(x,y) – E(X) E(Y)

The covariance will have the same units as the variance and is therefore affected by the unit chosen to measure the data.

Therefore, we also define the correlation, which is unitless.

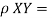cov (X,Y)

Example:

An apartment manager decides to see if timely payment of rent is related to unpaid credit card balances. Using XX as the number of unpaid credit card balances, and YY as the number of timely rent payments in the last four months, he examines his records and the credit reports of his renters and obtains the following results.

By inspection of the table, we can answer some basic probability questions.

• The percentage of renters with exactly 3 timely payments and 1 unpaid credit card balance is   PXY(X=1,Y=3)=0.11PXY(X=1,Y=3)=0.11.
• The percentage of renters with exactly 3 timely payments is   PY(Y=3)=0.26PY(Y=3)=0.26.
• The percentage of renters with exactly 1 unpaid credit card balance is PX(X=1)=0.29PX(X=1)=0.29.

The expected value (or mean) of each random variable can be found by use of the formulas.

E(X)E(Y)=∑all xPX(x)=0(0.24)+1(0.29)+2(0.33)+3(0.14)=1.37

=∑all yPY(y)=0(0.11)+1(0.17)+2(0.24)+3(0.26)+4(0.22)=2.31

E(X)=∑all xPX(x)=0(0.24)+1(0.29)+2(0.33)+3(0.14)=1.37

E(Y)=∑all yPY(y)=0(0.11)+1(0.17)+2(0.24)+3(0.26)+4(0.22)=2.31

The renters at this apartment complex have a mean of 1.37 unpaid credit card balances, and a mean of 2.31 timely rent payments in the last four months. In other words, if one renter was randomly selected, we could expect to find a renter with 1.37 unpaid credit card balances and 2.31 timely rent payments.

We can also use the formulas to compute the variance and standard deviation of each random variable.

Var(X)= 2 Px(x) – E(X) 2

= 0 2   (0.24) + 1 2 (0.29) + 2 2 (0.33) + 3 2(0.14) -1.37 2 = 0.9931 (0.24)+12(0.29)+22(0.33)+32(0.14)−1.372=0.9931

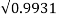= = 0.9965

Var(Y)=∑all y2PY(y)−(E(Y))2=02(0.11)+12(0.17)+22(0.24)+32(0.26)+42(0.22)−2.312=1.6539

σY=1.6539=1.2860

Interpreting these results, we find variances of 0.9931 squared balances and 1.6539 squared rent payments. But since the squared units of variance are somewhat unclear, we generally favour the standard deviations of 0.9965 balances and 1.2860 rent payments.

To obtain the strength of any relationship between these variables, we can compute the covariance.

Cov(X,Y)=∑all x∑all yxyPXY(x,y)−E(X)E(Y)=0(0)(0.01)+0(1)(0.02)+0(2)(0.03)+0(3)(0.05)+0(4)(0.13)

+1(0)(0.01)+1(1)(0.04)+1(2)(0.08)+1(3)(0.11)+1(4)(0.05)

+2(0)(0.06)+2(1)(0.07)+2(2)(0.09)+2(3)(0.08)+2(4)(0.03)

+3(0)(0.03)+3(1)(0.04)+3(2)(0.04)+3(3)(0.02)+3(4)(0.01)−(1.37)(2.31)

=−0.5547

Since the covariance is nonzero, the variables are not independent, but do have some sort of relationship. Since the covariance is negative, the relationship is an inverse relationship, where the increase in credit card balances generally decreases the timeliness of rent payments. But to determine the strength of the relationship, we need to evaluate the correlation.

With   ρXY=−0.4329ρXY=−0.4329, we find that there is a moderate negative relationship between the number of credit card balances and the timeliness of rent payments.

3.3Moments of random variable

The “moments” of a random variable (or of its distribution) are expected values of powers or related functions of the random variable.

The r th moment of X is E(Xr ). In particular, the first moment is the mean, µX = E(X). The mean is a measure of the “center” or “location” of a distribution. Another measure of the “center” or “location” is a median, defined as a value m such that P(X < m) ≤ 1/2 and P(X ≤ m) ≥ 1/2.

If there is only one such value, then it is called the median.

The r th central moment of X is E[(X −µX) r ]. In particular, the second central moment is the variance, σ2 X = V ar(X) = E[(X −µX) 2 ].

The standard deviation of a random variable is the (nonnegative) square root of the variance: σX = Sd(X) = q σ2X .

The variance and standard deviation are measures of the spread or dispersion of a distribution. The standard deviation is measured in the same units as X, while the variance is in X-units squared.

Another measure of spread is the mean (absolute) deviation:

M.A.D. = E(|X − m|) where m is the median of the distribution of X. This is a  natural measure of spread than the standard deviation or the variance.

3.4 Conditional Distribution

A Safety Officer for an auto insurance company in Connecticut was interested in learning how the extent of an individual's injury in an automobile accident relates to the type of safety restraint the individual was wearing at the time of the accident. As a result, the Safety Officer used state-wide ambulance and police records to compile the following two-way table of joint probabilities:

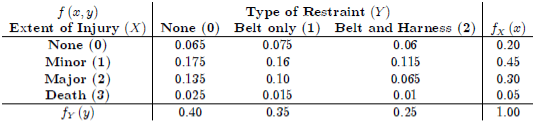
For the sake of understanding the Safety Officer's terminology, let's assume that "Belt only" means that the person was only using the lap belt, whereas "Belt and Harness" should be taken to mean that the person was using a lap belt and shoulder strap. Also, note that the Safety Officer created the random variable X, the extent of injury, by arbitrarily assigning values 0, 1, 2, and 3 to each of the possible outcomes None, Minor, Major, and Death. Similarly, the Safety Officer created the random variable Y, the type of restraint, by arbitrarily assigning values 0, 1, and 2 to each of the possible outcomes None, Belt Only, and Belt and Harness.

Among other things, the Safety Officer was interested in answering the following questions:

• What is the probability that a randomly selected person in an automobile accident was wearing a seat belt and had only a minor injury?
• If a randomly selected person wears no restraint, what is the probability of death?
• If a randomly selected person sustains no injury, what is the probability the person was wearing a belt and harness?

What is the probability a randomly selected person in an accident was wearing a seat belt and had only a minor injury?

Solution

Let A = the event that a randomly selected person in a car accident has a minor injury. Let B = the event that the randomly selected person was wearing only a seat belt. Then, just reading the value right off of the Safety Officer's table, we get:

P(A and B)=P(X=1,Y=1)=f(1,1)=0.16

That is, there is a 16% chance that a randomly selected person in an accident is wearing a seat belt and has only a minor injury.

In order to define the joint probability distribution of X and Y fully, we'd need to find the probability that X=x and Y=y for each element in the joint support SS, not just for one element X=1 and Y=1.

Conditional Probability Distribution

A conditional probability distribution is a probability distribution for a sub-population. That is, a conditional probability distribution describes the probability that a randomly selected person from a sub-population has the one characteristic of interest.

Example (continued)

If a randomly selected person wears no restraint, what is the probability of death?

Solution

We see the Safety Officer is wanting to know a conditional probability. So, we need to use the definition of conditional probability to calculate the desired probability.

But, let's first dissect the Safety Officer's question into two parts by identifying the subpopulation and the characteristic of interest. Well, the subpopulation is the population of people wearing no restraints ( NR ), and the characteristic of interest is death (DD). Then, using the definition of conditional probability, we determine that the desired probability is:

P(D|NR)=P(D∩NR)/P(NR)=P(X=3,Y=0)/P(Y=0)=f(3,0)/fY(0)=0.025/0.40=0.0625

That is, there is a 6.25% chance of death of a randomly selected person in an automobile accident, if the person wears no restraint.

3.5 Densities and Moments

Probability densities are like other densities; they're derivatives. The probability density function f is the derivative of the cumulative distribution function F of the random variable X. Thus,

f(x)=limh→0F(x+h)−F(x)h
=limh→0P(X∈[x,x+h])h

So f(x) is about equal to the probability that X lies in the interval I = [x,x+h] divided by the length h of the interval I.

Moments

Moments are a set of statistical parameters to measure a distribution. Four moments are commonly used:

• 1st, Mean: the average
• 2d, Variance:
  • Standard deviation is the square root of the variance: an indication of how closely the values are spread about the mean.
• 3d, Skewness: measure the asymmetry of a distribution about its peak; it is a number that describes the shape of the distribution.
  • It is often approximated by Skew = (Mean - Median) / (Std dev).
  • If skewness is positive, the mean is bigger than the median and the distribution has a large tail of high values.
  • If skewness is negative, the mean is smaller than the median and the distribution has a large tail of small values.
• 4th: Kurtosis: measures the peakness or flatness of a distribution.
  • Positive kurtosis indicates a thin pointed distribution.
  • Negative kurtosis indicates a broad flat distribution.

3.6 Characteristic functions of random variable

There are random variables for which the moment generating function does not exist on any real interval with positive length. For example, consider the random variable X that has a Cauchy distribution

FX(x)=1π/1+x2,for all x∈R.

For any nonzero real number s

MX(s)=∫∞−∞esx1/π/1+x2dx = ∞

Therefore, the moment generating function does not exist for this random variable on any real interval with positive length. If a random variable does not have a well-defined MGF, we can use the characteristic function defined as

ΦX(ω)=E[ejωX],

Where j= √−1 and ωis a real number.

It is worth noting that ejω is a complex-valued random variable. The complex random variable can be written as X=Y+jZ, where Y and Z are ordinary real-valued random variables. Thus, working with a complex random variable is like working with two real-valued random variables. The advantage of the characteristic function is that it is defined for all real-valued random variables. Specifically, if X is a real-valued random variable, we can write

|ejωX|=1.

Therefore, we conclude

|ϕX(ω)|=|E[ejωX]|≤E[|ejωX|]≤1

The characteristic function has similar properties to the MGF.

For example, if X and Y are independent

ϕX+Y(ω)=E[ejω(X+Y)]

=E[ejωXejωY]=E[ejωX]E[ejωY](since X and Y are independent

=ϕX(ω)ϕY(ω).

More generally, if X1, X2, ..., Xn are n independent random variables, then

ϕX1+X2+⋯+Xn(ω)=ϕX1(ω)ϕX2(ω)⋯ϕXn(ω).

3.7 Markov

Consider an object that moves in random manner. This object could be a football, a chess player making his/her next move, exchange rates, stock price, car movement, the position of a customer in a queue, a person moving on the road, players on a football field, etc.

If an object moves in a random fashion its movements are memoryless then that object has a Markov property.

For instance let’s consider that our target object is a football being kicked around by a group of football players. The football can be in any state next. We stated that Markov property is memoryless. It implies that the future movement of the object depends only on its present state.

What is Markov chain?

Let’s consider that an object moves in a random manner. Therefore, the state of the object (or system) can change. This change is known as the transition and each transition has a probability associated with other transitions.

Consequently, the mathematical system which makes transition from one state to another is based on a probability.

This system is an example random process. Let’s assume that it can be in state A or B. Let’s also consider that when the object is in state A then there is a 40% chance that it will remain in the state A and 60% chance that it will be transitioned into state B as demonstrated below:

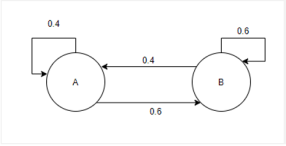
Example state machine

The key to note is that the process has a Markov property, which implies that it is memoryless. As a result, the probability of future transitions is not dependent on the past states. They only depend on the current state. This is the reason why we consider it to be memoryless.

Components Of Markov Chain

The two main components of a Markov chain:

State Space

The state space is the set of all possible states (places) that a random system can be in.

It is denoted as S. As an instance, S can be {up, down} or {top, bottom} or {1.1,2.2,…} or {positive, negative, neutral} or {AAA,AA,A, B, D, E..} etc.

Transition Probabilities

The second component is the transition probabilities. The transition probabilities are a table of probabilities. Each entry i, j in the table informs us about the probability of an object transitioning from state i to state j.

3.8 Chebyshev and Chernoff Bounds

If X is a random variable, then for any a∈R, we can write

P(X≥a)=P(esX≥esa), for s>0

P(X≤a)=P(esX≥esa), for s<0.

esX is always a positive random variable for all s∈R.

Thus, we can apply Markov's inequality.

So, for s>0, we can write

P(X≥a)=P(esX≥esa)≤E[esX]/esa, by Markov's inequality.

Similarly, for s<0, we can write

P(X≤a)=P(esX≥esa)≤E[esX]/esa.

Note that E[esX] is in fact the moment generating function, MX(s). Thus, we conclude

Chernoff Bounds:

P(X≥a)≤e−saMX(s), for all s>0,

P(X≤a)≤e−saMX(s), for all s<0

Since Chernoff bounds are valid for all values of s>0 and s<0, we can choose s in a way to obtain the best bound, that is we can write

P(X≥a)P(X≤a)≤mins>0e−saMX(s),≤mins<0e−saMX(s).

Chebyshev bounds:

If X is a random variable with E[X] = µ and Var(X) = σ2 :

P(|X −µ| ≥ k) ≤σ2/ k 2 for all k > 0

Let Y = (X −µ) 2 . Then E[Y] = Var(X) = σ2 . Applying Markov’s inequality to Y with a = k 2 gives us

P(Y ≥ k 2 ) ≤ E[Y] k 2

P((X −µ) 2≥ k 2 ) ≤ Var(X) / k 2

P(|X −µ| ≥ k) ≤σ2/k 2

The intuition is also similar: if we know the expectation and the probability that X is at least k away from the expectation (in either direction), then minimizing the variance means pushing the probability mass inside the interval (µ− k, µ+ k) all inward to µ, and pushing the probability mass outside that interval inward to µ± k. So, the smallest variance possible is

σ2 = E[(X −µ) 2 ] ≥ 0 2 . P(|X −µ| = 0) + k 2· P(|X −µ| = k) = k 2· P(|X −µ| ≥ k)

There’s also a pair of “one-sided” inequalities named after Chebyshev, which say that

P(X ≥ µ + a) ≤ σ2/ σ2 + a 2

P(X ≤µ− a) ≤σ2/ σ2 + a 2

An example has a mean score of 82.2 out of 120 and a standard deviation of 18.5 (variance σ 2 = 342.25). What’s highest possible fraction of students that scored at least 100?

Solution:

Assuming scores are nonnegative,

Markov’s inequality tells us that P(X ≥ 100) ≤ E[X] 100 = 0.822

The one-sided Chebyshev’s inequality tells us P(X ≥ 100 = 82.2 + 17.8) ≤ σ 2 σ2 + 17.8 2 = 342.25 342.25 + 17.8 2 ≈ 0.519

We can see that Chebyshev’s inequality gives us a tighter bound. This is because we know the variance in addition to the mean.

Still, both are very loose bounds; the actual fraction who got greater than 100 on this exam was 0.109.

References