UNIT 5
Ground Wave Propagation

Figure 5.1. Plane Earth Reflection
Key takeaways:

Figure 5.2. Space Wave Propagation
Space wave propagation depends on three components:
Dm = (2RHt)-½ + (2RHr)-½
Where,
Dm: the distance between the two antennas
R: radius of the earth
Ht: height of transmission antenna
Hr: height of receiver antenna
5.2.1. Applications
It is used in various communication systems like
5.2.2. Limitations
Key takeaways:
5.3.1. Rayleigh waves
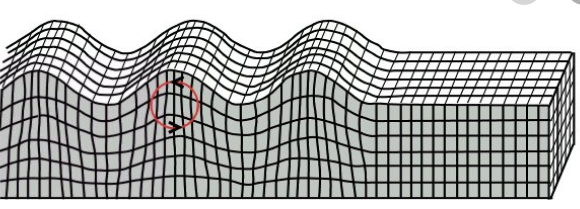
Figure 5.3.1. Rayleigh waves

Key takeaways:
5.4.1. Introduction
5.4.2. Principle used in space wave propagation

Figure 5.4.2. The principle used in space wave propagation
5.4.3. Field strength
dd = 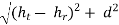
 d
d 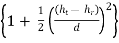
dr = 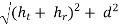
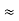 d
d 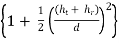
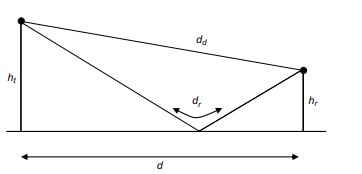
Figure 5.4.3. The geometry of space wave propagation
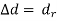 -
-  =
= 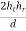
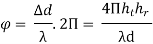
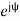
5.4.4. Effect of curvature of the earth
5.4.5. Effect of Imperfection of earth
5.4.6. Limitations of space wave Propagation
Key takeaways:
References
Unit - 4
Turing machines
An information processing system (TM) may be a mathematical model that consists of
Associate infinite length tape divided into cells on which input is given. It consists of a head that reads the input tape.
A state register stores the state of the information processing system. Once reading an associated input image, it’s replaced with another image, its internal state is modified, and it moves from one cell to the proper or left. If the metal reaches the ultimate state, the input string is accepted, otherwise rejected.
A metal will be formally delineate as a 7-tuple (Q, X, ∑, δ, q0, B, F)
Where −
• Q may be a finite set of states
• X is that the tape alphabet
• ∑ is that the input alphabet
• δ may be a transition function; δ : alphabetic character × X → alphabetic character × X ×
• q0 is that the initial state
• B is that the blank image
• F is that the set of ultimate states
Basic model of turing machine
With the help of the following representation, the turning machine can be modelled.
- The input tape contains an infinite number of cells, each cell containing one input symbol, so it is possible to position the input string on the tape. Blank characters fill up the empty tape.

Fig 1: Input tape
2. The finite control and the head of tape that is responsible for reading the current symbol of input. The head of the tape will switch from left to right,
3. A finite set of states through which the system has to go through.
4. Finite set of symbols that are used in the construction of the turing machine logic, called external symbols.
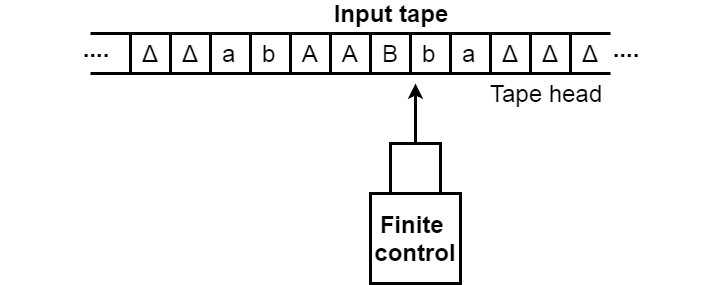
Fig 2: Basic model of TM
Various features of the Turing machine exist:
● It has an external memory that recalls an arbitrary, long input list.
● It has infinite capability for memory.
● The model has a method in which it is easy to read the input on the tape on the left or right.
● Depending on its input, the computer may generate a certain output. It will often be appropriate for the same input to be used to produce the output. So, the distinction between input and output has been abolished in this machine. It is therefore possible to use a standard set of alphabets for the Turing machine.
Key takeaway:
- TM may be a mathematical model that consists of associate infinite length tape divided into cells on which input is given.
- It consists of a head that reads the input tape.
- A state register stores the state of the information processing system.
A language is termed Decidable or algorithmic if there’s a data processor that
Accepts and halts on each input string w. Each decidable language is Turing-
Acceptable.
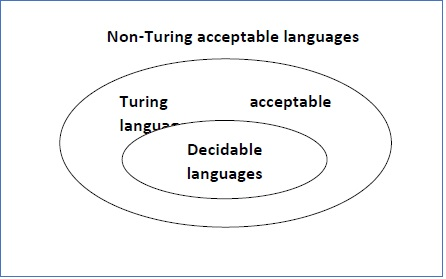
Fig 3: Decidable language
A decision downside P is decidable if the language L of all affirmative instances to P
Is decidable.
For a decidable language, for every input string, the thulium halts either at the settle
For or the reject state as pictured within the following diagram -
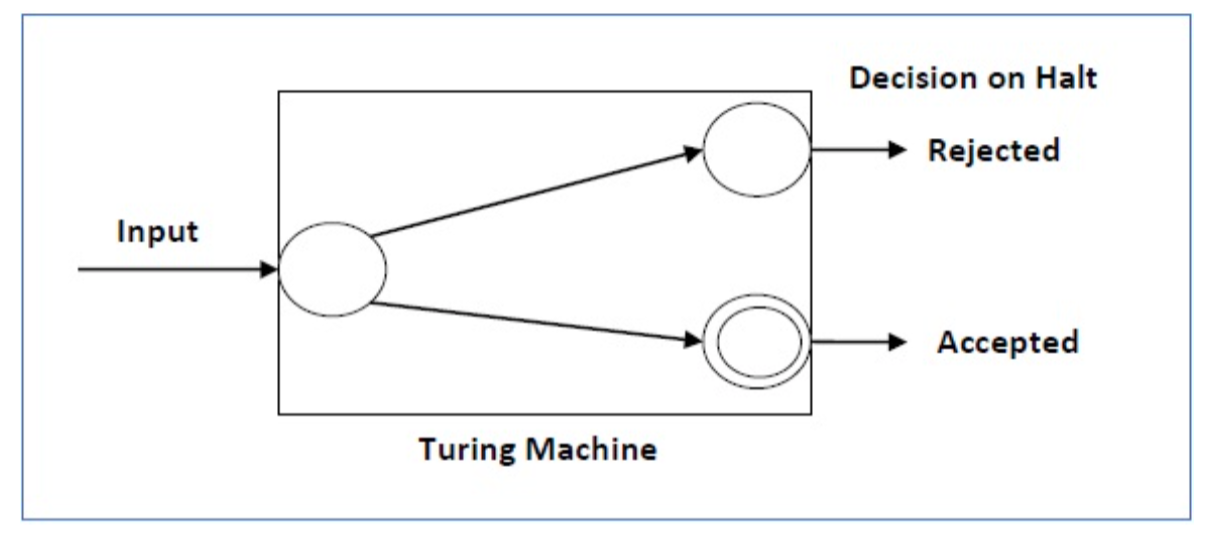
Fig 4: shows different state
Example 1
Find out whether or not the subsequent downside is decidable or not − Is a range ‘m’ prime?
Solution
Prime numbers =
Divide the amount ‘m’ by all the numbers between ‘2’ and ‘√m’ ranging from ‘2’.
If any of those numbers turn out a remainder zero, then it goes to the “Rejected
State”, otherwise it goes to the “Accepted state”. So, here the solution may well be
Created by ‘Yes’ or ‘No’.
Hence, it’s a decidable downside.
Example 2
Given an everyday language L and string w, however will we have a tendency to
Check if w ∈ L?
Solution
Take the DFA that accepts L and check if w is accepted
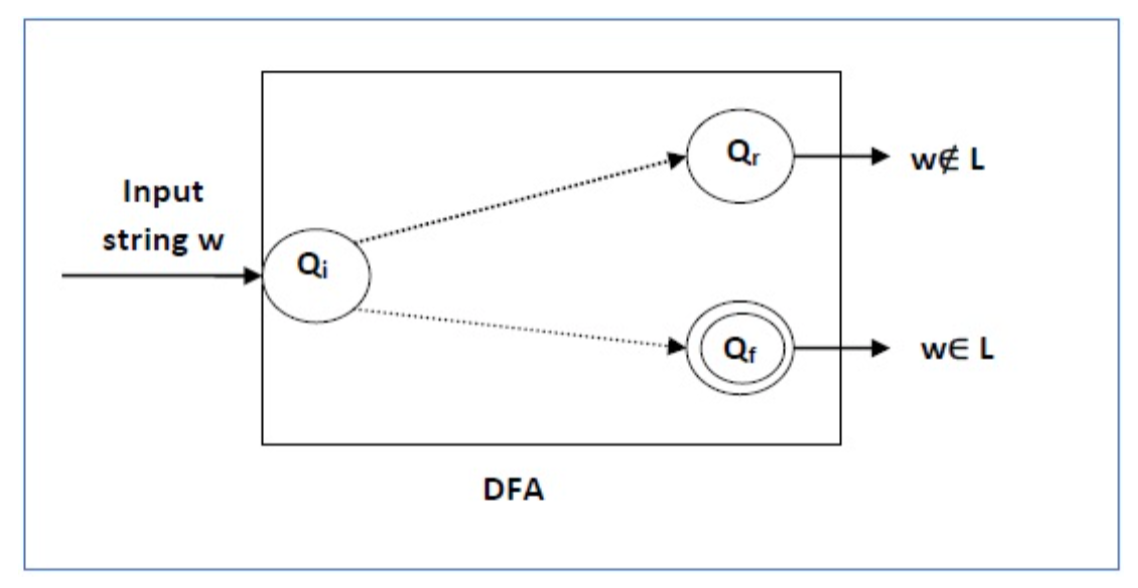
Fig 5: DFA diagram
Some additional decidable issues are -
• Does DFA settle for the empty language?
• Is L1 ∩ L2 = ∅ for normal sets?
Key takeaway:
- If a language L is decidable, then its complement L’ is additionally decidable
- If a language is decidable, then there’s AN functionary for it.
4.2.1 Closure properties
- Union and Intersection
Recursive
L1 x L2 and L1 x L2 are both recursive if L1 is recursive and L2 is recursive.
Using a multitape TM:
● Copy to Tape 2 and Tape 3 inputs
● Run M1 to tape 2 and M2 to tape 3 (neither will run forever; i.e.we get a result)
● They will determine whether x is in L1 and/or L2
● Test if approved by both M1 and M2 (intersection)
● Test if one is approved by M1 and M2 (union)
If L1 and L2 are recursive, the difference between L1 - L2=L1 and L2 is recursive.
Recursively Enumerable
If L1 and L2 are enumerated recursively, then L1 ∪ L2 and L1 ∩ L2 are recursively enumerated .
● Similar to the recursive case, but the case where M1 and M2 will run constantly
● Simulate simultaneously running M1 and M2-alternate one move from each machine.
A union, for reference,
● If any computer ever accepts it, accept it.
● If any machine ever refuses or fails, then the other machine continues to run.
If L is enumerated recursively and L is enumerated recursively, L is enumerated recursively.
● Let M and M be TMs, respectively, that accept L and L.
● Simultaneously, Run M and M'
● It must be agreed for any term x by any one of M or M'
● Therefore, either M or M 'will stop and agree
● If M stops and agrees, then stop and embrace.
● If M' stops and embraces, then stop and deny.
The TM that runs M and M at the same time always stops and accepts or refuses so that L and L are recursive.
If L is enumerable recursively, and L is not recursive, then L is not enumerable recursively.
- Concatenation
If L1 and L2 are two recursive languages, the L1.L2 concatenation would also be recursive. For instance:
L1 = {anbncn|n>=0}
L2 = {dmemfm|m>=0}
L3 = L1.L2
= {anbncndn emfm|m>=0 and n>=0} is also recursive.
L1 states that n no. Of a's is followed by n no. Of b's, and n no. Of c's. L2 says that m no. Of d's is followed by m no. Of e's, m no. Of f's. First, their concatenation matches no. Of a's, b's, and c's, then no. Of d's, e's, and f's. It can therefore be determined by TM.
- Kleene Closure
If L1 is recursive, its L1* smaller closure would also be recursive. For instance:
L1 = {anbncn|n>=0}
L1*= { anbncn||n>=0}* is also recursive.
1. Multiple tracks Alan Turing Machine:
● A k-tack Alan Turing machine (for some k>0) has k-tracks and one R/W head
That reads and writes all of them one by one.
● A k-track information processing system may be simulated by one track information processing system.
2. Two-way infinite Tape Alan Turing Machine:
● Infinite tape of two-way infinite tape information processing system is
Boundless in each direction left and right.
● Two-way infinite tape information processing system may be simulated by
Unidirectional infinite {turing|Turing|Alan Alan Turing|Alan Mathison
Turing|mathematician} machine (standard Turing machine).
3. Multi-tape Alan Turing Machine:
● It has multiple tapes and is controlled by one head.
● The Multi-tape information processing system is completely different from the k-track information processing system however communicative power is the same.
● Multi-tape information processing system may be simulated by a single-tap information processing system.
4. Multi-tape Multi-head Alan Turing Machine:
● The multi-tape information processing system has multiple tapes and multiple Heads.
● Each tape is controlled by a separate head.
● Multi-Tape Multi-head information processing systems may be simulated by normal information processing systems.
5. Multi-dimensional Tape Alan Turing Machine:
● It has multi-dimensional tape wherever the head will move any direction that’s left, right, up or down.
● Multi-dimensional tape information processing system may be simulated by a one-dimensional information processing system.
6. Multi-head Alan Turing Machine:
● A multi-head information processing system contains 2 or additional heads to scan the symbols on constant tape.
● In one step all the heads sense the scanned symbols and move or write severally.
● Multi-head information processing system may be simulated by single head information processing system.
7. Non-deterministic Alan Turing Machine:
● A non-deterministic information processing system encompasses a single, a method infinite tape.
● For a given state and input image has at least one option to move (finite range of decisions for consecutive move), every selection has many decisions of path that it’d follow for a given input string.
● A non-deterministic information processing system is an adored settled information processing system.
In a Non-Deterministic computing device, for each state and image, there area unit a
Bunch of actions the thulium will have. So, here the transitions don’t seem to be
Settled. The computation of a non-deterministic computing device could be a tree of
Configurations which will be reached from the beginning configuration.
An input is settled fored if there’s a minimum of one node of the tree that is associate degree accept configuration, otherwise it’s not accepted. If all branches of the machine tree halt on all inputs, the non-deterministic computing device is named a Decider and if for a few inputs, all branches area unit rejected, the input is additionally rejected.
A non-deterministic computing device are often formally outlined as a 6-tuple
(Q, X,∑, δ, q0, B, F) where −
● Q could be a finite set of states
● X is that the tape alphabet
● ∑ is that the input alphabet
● δ could be a transition function;
δ: letter × X → P (Q × X ×).
● q0 is that the initial state
● B is that the blank image
● F is that the set of ultimate states
Key takeaway:
- In a Non-Deterministic Turing Machine, there is a group of acts the TM can have for every state and symbol. So, the transformations aren't deterministic here.
- A non-deterministic Turing Machine calculation is a tree of configurations that can be accessed from the configuration at the start.
Unrestricted Grammars
Recall, a descriptive linguistics is Associate in Nursing abstract entity that makes an
Attempt to explain the “strings” [aka sentences] of a language. As a proper extension
Of a context-free grammar:
Definition: Associate in Nursing unrestricted descriptive linguistics could be a 4-tuple (T,N,P,S), consisting of :
1. T = set of terminals (the legal “tokens” of the language)
2. N = set of nonterminals (aka variables)
3. P = as set of productions, every of the form:
v -> w (what will this mean?)
Where v and w area unit strings consisting of nonterminals and terminals.
4. S = a special nonterminal referred to as the beginning image.
This type of descriptive linguistics is additionally referred to as a sort zero descriptive linguistics. It’s such a computing device. [What will this mean? Given a sort zero descriptive linguistics, there exists a metallic element which will “recognize” identical language as that descriptive linguistics. And, conversely, a sort zero descriptive linguistics will continuously be found for the language recognized or generated by any metallic element.]
It is conjointly such as a recursively calculable language. [What will this mean?]
E.g.: G with set of productions:
P =
L(G) (language generated or recognized by G) =
w = ai {and i = 2k, k > 0}
Note: traditional methodology of specifying repetition of strings.
Definition: context-sensitive descriptive linguistics [aka kind one grammar]
All productions area unit of kind
v -> w wherever |v| < |w|
Note: one special traditional kind [what will this mean?] of this sort of descriptive
Linguistics needs productions of form:
UAv -> uwv with w != letter of the alphabet,
I.e., A -> w however solely within the context of u nine v.
A context-sensitive descriptive linguistics is such as a linear finite automaton (LBA)
And to a context-sensitive language.
Almost all languages area unit context-sensitive. [What will this mean exactly? -
They’ll really be less complicated than context-sensitive.]
Definition: context-free descriptive linguistics [aka kind a pair of grammar]
All productions area unit of the form:
A -> x — wherever A is nonterminal, x could be a string of nonterminals and Terminals.
A context-free descriptive linguistics is such as a pushdown automaton (PDA) and to
Context-free languages.
Definition: Regular descriptive linguistics [aka kind three descriptive linguistics, aka
Linear grammar]
All productions area unit of the form:
A -> wB
A -> w wherever A, B area unit nonterminals,
w could be a string of terminals
Regular grammars area unit such as regular sets [what will such as mean here?]
And they are such as finite automata.
Key takeaway:
- Once this constraint is removed, it is interesting to explore the possibilities.
- In fact, such grammars are called unrestricted grammars, where any combination of variables and terminals will appear on the left side.
Fig 5: Enumerator
Enumerator
(Q , Σ ,「,δ , qstart , qhalt )
δ : Q x「 → Q x「 {L , R}
x (Σ x{R} ) ∪ {(ε , S)}
Description
Use Enumeration attribute if you have got fields or properties of enumerated sorts
And you wish to save lots of them within the info. Victimization functionary you outline
However the enumerated values are saved and loaded from the info. The functionary
Attribute should be declared right higher than the enumerated sort.
Creator
Constructor Create(MappedType: TEnumMappingType); overload;
Constructor Create(MappedType: TEnumMappingType; MappedValues: string);
Overload;
Parameters
MappedType Indicated the kind of the enumerated worth within the info. Valid values square measure (prefixed by TEnumMappingType):
EmChar Enumerated values are saved as single-chars within the info
EmInteger Enumerated values are saved as number values. {the worth|the worth}
Used is that the ordinal value of the enumerated sort, i.e, the primary worth within the functionary are saved as zero, the second as one, etc..
EmString Enumerated values are saved as strings within the info
MappedValues If MappedType is char or string, then you need to use this
Parameter to specify the char/string worths reminiscent of every enumerated value.
The values should be comma-separated and should be within the same order
Because the values within the enumerated sort.
References:
- John E. Hopcroft, Rajeev Motwani and Jeffrey D. Ullman, Introduction to
Automata Theory, Languages, and Computation, Pearson Education Asia.
2. John Martin, Introduction to Languages and the Theory of Computation, Tata McGraw Hill.
3. Harry R. Lewis and Christos H. Papadimitriou, Elements of the Theory of Computation, Pearson EducationAsia.