Unit - 2
Statistical Decision Theory
One of the most significant developments in the probability field has been the development of Bayesian decision theory which has proved to be of immense help in making decisions under uncertain conditions. The Bayes Theorem was developed by a British Mathematician Rev. Thomas Bayes. The probability given under Bayes theorem is also known by the name of inverse probability, posterior probability or revised probability. This theorem finds the probability of an event by considering the given sample information; hence the name posterior probability. The bayes theorem is based on the formula of conditional probability.
Conditional probability of event A1 given event B
P(A1/B)=P(A1 and B)P(B)
Similarly probability of event A1 given event B
P(A2/B)=P(A2 and B)P(B)
Where
P(B)=P(A1 and B)+P(A2 and B)P(B)=P(A1)×P(B/A1)+P(A2)×P(BA2)
P(A1/B)P(A1/B) can be rewritten as
One of the most significant developments in the probability field has been the development of Bayesian decision theory which has proved to be of immense help in making decisions under uncertain conditions. The Bayes Theorem was developed by a British Mathematician Rev. Thomas Bayes. The probability given under Bayes theorem is also known by the name of inverse probability, posterior probability or revised probability. This theorem finds the probability of an event by considering the given sample information; hence the name posterior probability. The bayes theorem is based on the formula of conditional probability.
Conditional probability of event A1 given event B is
P(A1/B)=P(A1 and B)/P(B)
Similarly probability of event A1 given event B is
P(A2/B)=P(A2 and B)/P(B)
Where
P(B)=P(A1 and B)+P(A2 and B)P(B)=P(A1)×P(B/A1)+P(A2)×P(BA2)
P(A1/B) can be rewritten as
P(A1/B)=P(A1)×P(B/A1)/P(A1)×P(B/A1)+P(A2)×P(BA2)
Hence the general form of Bayes Theorem is
P(Ai/B)=P(Ai)×P(B/Ai)/ ∑ki=1P(Ai)×P(B/Ai)
Where A1, A2...Ai...An are set of n mutually exclusive and exhaustive events. Hence the general form of Bayes Theorem is
P(Ai/B)=P(Ai)×P(B/Ai)∑i=1kP(Ai)×P(B/Ai)
Where A1A1, A2A2...AiAi...AnAn are set of n mutually exclusive and exhaustive events.
Bayesian Learning
Imagine a situation where your friend gives you a new coin and asks you the fairness of the coin (or the probability of observing heads) without even flipping the coin once. In fact, you are also aware that your friend has not made the coin biased. In general, you have seen that coins are fair, thus you expect the probability of observing heads is 0.5. In the absence of any such observations, you assert the fairness of the coin only using your past experiences or observations with coins.
Suppose that you are allowed to flip the coin 10 times in order to determine the fairness of the coin. Your observations from the experiment will fall under one of the following cases:
Case 1: observing 5 heads and 5 tails.
Case 2: observing h heads and 10-h tails, where h ≠ 10−h.
If case 1 is observed, you are now more certain that the coin is a fair coin, and you will decide that the probability of observing heads is 0.5 with more confidence. If case 2 is observed, you can either:
Neglect your prior beliefs since now you have new data and decide the probability of observing heads is h/10 by solely depending on recent observations.
Adjust your belief accordingly to the value of h that you have just observed, and decide the probability of observing heads using your recent observations.
The first method suggests that we use the frequentist method, where we omit our beliefs when making decisions. However, the second method seems to be more convenient because 10 coins are insufficient to determine the fairness of a coin. Therefore, we can make better decisions by combining our recent observations and beliefs that we have gained through our past experiences. It is this thinking model that uses our most recent observations together with our beliefs or inclination for critical thinking that is known as Bayesian thinking.
Moreover, assume that your friend allows you to conduct another 10 coin flips. Then, we can use these new observations to further update our beliefs. As we gain more data, we can incrementally update our beliefs increasing the certainty of our conclusions. This is known as incremental learning, where you update your knowledge incrementally with new evidence.
Bayesian learning comes into play on such occasions, where we are unable to use frequentist statistics due to the drawbacks that we have discussed above. We can use Bayesian learning to address all these drawbacks and even with additional capabilities (such as incremental updates of the posterior) when testing a hypothesis to estimate unknown parameters of a machine learning models. Bayesian learning uses Bayes' theorem to determine the conditional probability of a hypotheses given some evidence or observations.
KEY TAKEAWAYS
- Bayesian networks are probabilistic, because these networks are built from a probability distribution, and also use probability theory for prediction and anomaly detection.
Real world applications are probabilistic in nature, and to represent the relationship between multiple events, we need a Bayesian network. It can also be used in various tasks including prediction, anomaly detection, diagnostics, automated insight, reasoning, time series prediction, and decision making under uncertainty.
- The Bayesian network has mainly two components:
- Causal Component
- Actual numbers
Each node in the Bayesian network has condition probability distribution P(Xi |Parent(Xi) ), which determines the effect of the parent on that node.
Bayesian network is based on Joint probability distribution and conditional probability.
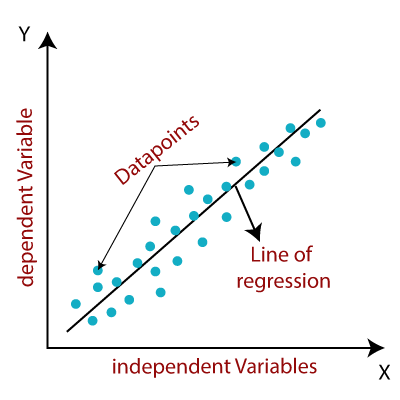
Linear regression is one of the easiest and most popular Machine Learning algorithms. It is a statistical method that is used for predictive analysis. Linear regression makes predictions for continuous/real or numeric variables such as sales, salary, age, product price, etc.
Linear regression algorithm shows a linear relationship between a dependent (y) and one or more independent (y) variables, hence called as linear regression. Since linear regression shows the linear relationship, which means it finds how the value of the dependent variable is changing according to the value of the independent variable.
The linear regression model provides a sloped straight line representing the relationship between the variables.
Mathematically, we can represent a linear regression as:
y= a0+a1x+ ε
Here,
Y= Dependent Variable (Target Variable)
X= Independent Variable (predictor Variable)
a0= intercept of the line (Gives an additional degree of freedom)
a1 = Linear regression coefficient (scale factor to each input value).
ε = random error
 |
Ridge regression
Ridge Regression is a technique for analyzing multiple regression data that suffer from multicollinearity. When multicollinearity occurs, least squares estimates are unbiased, but their variances are large so they may be far from the true value. By adding a degree of bias to the regression estimates, ridge regression reduces the standard errors. It is hoped that the net effect will be to give estimates that are more reliable. Another biased regression technique, principal components regression, is also available in NCSS.
Ridge regression is the more popular of the two methods.
Multicollinearity
Multicollinearity, or collinearity, is the existence of near-linear relationships among the independent variables. For example, suppose that the three ingredients of a mixture are studied by including their percentages of the total. These variables will have the (perfect) linear relationship: P1 + P2 + P3 = 100. During regression calculations, this relationship causes a division by zero which in turn causes the calculations to be aborted. When the relationship is not exact, the division by zero does not occur and the calculations are not aborted.
However, the division by a very small quantity still distorts the results. Hence, one of the first steps in a regression analysis is to determine if multicollinearity is a problem.
Effects of Multicollinearity
Multicollinearity can create inaccurate estimates of the regression coefficients, inflate the standard errors of the regression coefficients, deflate the partial t-tests for the regression coefficients, give false, nonsignificant, pvalues, and degrade the predictability of the model (and that’s just for starters).
Sources of Multicollinearity
To deal with multicollinearity, you must be able to identify its source. The source of the multicollinearity impacts the analysis, the corrections, and the interpretation of the linear model. There are five sources:
1. Data collection. In this case, the data have been collected from a narrow subspace of the independent variables. The multicollinearity has been created by the sampling methodology—it does not exist in the population. Obtaining more data on an expanded range would cure this multicollinearity problem. The extreme example of this is when you try to fit a line to a single point.
2. Physical constraints of the linear model or population. This source of multicollinearity will exist no matter what sampling technique is used. Many manufacturing or service processes have constraints on independent variables (as to their range), either physically, politically, or legally, which will create multicollinearity.
3. Over-defined model. Here, there are more variables than observations. This situation should be avoided.
4. Model choice or specification. This source of multicollinearity comes from using independent variables that are powers or interactions of an original set of variables. It should be noted that if the sampling subspace of independent variables is narrow, then any combination of those variables will increase the multicollinearity problem even further.
5. Outliers. Extreme values or outliers in the X-space can cause multicollinearity as well as hide it. We call this outlier-induced multicollinearity. This should be corrected by removing the outliers before ridge regression is applied.
Detection of Multicollinearity
There are several methods of detecting multicollinearity.
1. Begin by studying pairwise scatter plots of pairs of independent variables, looking for near-perfect relationships. Also glance at the correlation matrix for high correlations. Unfortunately, multicollinearity does not always show up when considering the variables two at a time.
2. Consider the variance inflation factors (VIF). VIFs over 10 indicate collinear variables.
3. Eigenvalues of the correlation matrix of the independent variables near zero indicate multicollinearity. Instead of looking at the numerical size of the eigenvalue, use the condition number. Large condition numbers indicate multicollinearity.
4. Investigate the signs of the regression coefficients. Variables whose regression coefficients are opposite in sign from what you would expect may indicate multicollinearity.
Correction for Multicollinearity
Depending on what the source of multicollinearity is, the solutions will vary. If the multicollinearity has been created by the data collection, collect additional data over a wider X-subspace. If the choice of the linear model has increased the multicollinearity, simplify the model by using variable selection techniques. If an observation or two has induced the multicollinearity, remove those observations. Above all, use care in selecting the variables at the outset. When these steps are not possible, you might try ridge regression.
Lasso regression
Lasso regression is a type of linear regression that uses shrinkage. Shrinkage is where data values are shrunk towards a central point, like the mean. The lasso procedure encourages simple, sparse models (i.e. models with fewer parameters). This particular type of regression is well-suited for models showing high levels of muti-collinearity or when you want to automate certain parts of model selection, like variable selection/parameter elimination.
The acronym “LASSO” stands for Least Absolute Shrinkage and Selection Operator.
Principal component regression
The principal component regression (PCR) first applies Principal Component Analysis on the data set to summarize the original predictor variables into few new variables also known as principal components (PCs), which are a linear combination of the original data.
These PCs are then used to build the linear regression model. The number of principal components, to incorporate in the model, is chosen by cross-validation (cv). Note that, PCR is suitable when the data set contains highly correlated predictors.
Partial least squares regression
A possible drawback of PCR is that we have no guarantee that the selected principal components are associated with the outcome. Here, the selection of the principal components to incorporate in the model is not supervised by the outcome variable.
An alternative to PCR is the Partial Least Squares (PLS) regression, which identifies new principal components that not only summarizes the original predictors, but also that are related to the outcome. These components are then used to fit the regression model. So, compared to PCR, PLS uses a dimension reduction strategy that is supervised by the outcome.
Like PCR, PLS is convenient for data with highly-correlated predictors. The number of PCs used in PLS is generally chosen by cross-validation. Predictors and the outcome variables should be generally standardized, to make the variables comparable.
KEY TAKEAWAYS
- The principal component regression (PCR) first applies Principal Component Analysis on the data set to summarize the original predictor variables into few new variables also known as principal components
- Partial Least Squares (PLS) regression, which identifies new principal components that not only summarizes the original predictors, but also that are related to the outcome.
- The probability given under Bayes theorem is also known by the name of inverse probability, posterior probability or revised probability. This theorem finds the probability of an event by considering the given sample information
- Multicollinearity, or collinearity, is the existence of near-linear relationships among the independent variables
- Linear regression algorithm shows a linear relationship between a dependent (y) and one or more independent (y) variables, hence called as linear regression.
References:
1. J. Shavlik and T. Dietterich (Ed), Readings in Machine Learning, Morgan Kaufmann, 1990.
2. P. Langley, Elements of Machine Learning, Morgan Kaufmann, 1995.
3. Understanding Machine Learning. Shai Shalev-Shwartz and Shai Ben-David. Cambridge University Press. 2017. [SS-2017]
4. The Elements of Statistical Learning. Trevor Hastie, Robert Tibshirani and Jerome Friedman. Second Edition. 2009. [TH-2009]