Unit - 4
Hypothesis testing
A statistical hypothesis is an assumption about a population which may or may not be true. Hypothesis testing is a set of formal procedures used by statisticians to either accept or reject statistical hypotheses. Statistical hypotheses are of two types:
- Null hypothesis- represents a hypothesis of chance basis.
- Alternative hypothesis- represents a hypothesis of observations which are influenced by some non-random cause.
Example: suppose we wanted to check whether a coin was fair and balanced. A null hypothesis might say, that half flips will be of head and half will of tails whereas alternative hypothesis might say that flips of head and tail may be very different.
H0:P=0.5Ha:P≠0.5H0:P=0.5Ha:P≠0.5
For example if we flipped the coin 50 times, in which 40 Heads and 10 Tails results. Using result, we need to reject the null hypothesis and would conclude, based on the evidence, that the coin was probably not fair and balanced.
Hypothesis Tests
Following formal process is used by statistician to determine whether to reject a null hypothesis, based on sample data. This process is called hypothesis testing and is consists of following four steps:
- State the hypotheses - This step involves stating both null and alternative hypotheses. The hypotheses should be stated in such a way that they are mutually exclusive. If one is true then other must be false.
- Formulate an analysis plan - The analysis plan is to describe how to use the sample data to evaluate the null hypothesis. The evaluation process focuses around a single test statistic.
- Analyze sample data - Find the value of the test statistic (using properties like mean score, proportion, t statistic, z-score, etc.) stated in the analysis plan.
- Interpret results - Apply the decisions stated in the analysis plan. If the value of the test statistic is very unlikely based on the null hypothesis, then reject the null hypothesis.
4.1.1Ensemble Methods
Ensembles can give us boost in the machine learning result by combining several models. Basically, ensemble models consist of several individually trained supervised learning models and their results are merged in various ways to achieve better predictive performance compared to a single model. Ensemble methods can be divided into following two groups −
Sequential ensemble methods
As the name implies, in these kind of ensemble methods, the base learners are generated sequentially. The motivation of such methods is to exploit the dependency among base learners.
Parallel ensemble methods
As the name implies, in these kind of ensemble methods, the base learners are generated in parallel. The motivation of such methods is to exploit the independence among base learners.
Ensemble Learning Methods
The following are the most popular ensemble learning methods i.e. the methods for combining the predictions from different models −
Bagging
The term bagging is also known as bootstrap aggregation. In bagging methods, ensemble model tries to improve prediction accuracy and decrease model variance by combining predictions of individual models trained over randomly generated training samples. The final prediction of ensemble model will be given by calculating the average of all predictions from the individual estimators. One of the best examples of bagging methods are random forests.
Boosting
In boosting method, the main principle of building ensemble model is to build it incrementally by training each base model estimator sequentially. As the name suggests, it basically combine several week base learners, trained sequentially over multiple iterations of training data, to build powerful ensemble. During the training of week base learners, higher weights are assigned to those learners which were misclassified earlier. The example of boosting method is AdaBoost.
Voting
In this ensemble learning model, multiple models of different types are built and some simple statistics, like calculating mean or median etc., are used to combine the predictions. This prediction will serve as the additional input for training to make the final prediction.
Bagging Ensemble Algorithms
The following are three bagging ensemble algorithms −
- Bagged Decision Tree
- Random Forest
- Extra Trees
Boosting Ensemble Algorithms
The followings are the two most common boosting ensemble algorithms −
- AdaBoost
- Stochastic Gradient Boosting
4.1.2 Bagging Adaboost Gradient Boosting
The term gradient boosting consists of two sub-terms, gradient and boosting. We already know that gradient boosting is a boosting technique.Let us see how the term ‘gradient’ is related here.
Gradient boosting re-defines boosting as a numerical optimisation problem where the objective is to minimise the loss function of the model by adding weak learners using gradient descent. Gradient descent is a first-order iterative optimisation algorithm for finding a local minimum of a differentiable function. As gradient boosting is based on minimising a loss function, different types of loss functions can be used resulting in a flexible technique that can be applied to regression, multi-class classification, etc.
Intuitively, gradient boosting is a stage-wise additive model that generates learners during the learning process (i.e., trees are added one at a time, and existing trees in the model are not changed). The contribution of the weak learner to the ensemble is based on the gradient descent optimisation process. The calculated contribution of each tree is based on minimising the overall error of the strong learner.
Gradient boosting does not modify the sample distribution as weak learners train on the remaining residual errors of a strong learner (i.e, pseudo-residuals). By training on the residuals of the model, this is an alternative means to give more importance to misclassified observations. Intuitively, new weak learners are being added to concentrate on the areas where the existing learners are performing poorly. The contribution of each weak learner to the final prediction is based on a gradient optimisation process to minimise the overall error of the strong learner.
Difference between Gradient Boosting and Adaptive Boosting(AdaBoost)
Gradient boosting | Adaptive Boosting |
This approach trains learners based upon minimising the loss function of a learner (i.e., training on the residuals of the model) | This method focuses on training upon misclassified observations. Alters the distribution of the training dataset to increase weights on sample observations that are difficult to classify. |
Weak learners are decision trees constructed in a greedy manner with split points based on purity scores (i.e., Gini, minimise loss). Thus, larger trees can be used with around 4 to 8 levels. Learners should still remain weak and so they should be constrained (i.e., the maximum number of layers, nodes, splits, leaf nodes) | The weak learners in case of adaptive boosting are a very basic form of decision tree known as stumps. |
All the learners have equal weights in the case of gradient boosting. The weight is usually set as the learning rate which is small in magnitude. | The final prediction is based on a majority vote of the weak learners’ predictions weighted by their individual accuracy. |
Clustering is somewhere similar to the classification algorithm, but the difference is the type of dataset that we are using. In classification, we work with the labeled data set, whereas in clustering, we work with the unlabelled dataset.
k-Nearest Neighbor Learning algorithm assumes all instances correspond to points in the n-dimensional space Rn
• The nearest neighbors of an instance are defined in terms of Euclidean distance. • Euclidean distance between the instances xi = and xj = are:
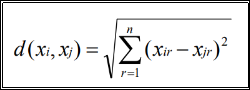
• For a given query instance xq, f(xq) is calculated the function values of k-nearest neighbor of xq
The KNN Algorithm assumes that similar things exist in close proximity. In other words, similar things stays near to each other.
- Load the data
- Initialize K to your chosen number of neighbours
3. For each example in the data
3.1 Calculate the distance between the query example and the current example from the data.
3.2 Add the distance and the index of the example to an ordered collection
4. Sort the ordered collection of distances and indices from smallest to largest (in ascending order) by the distances
5. Pick the first K entries from the sorted collection
6. Get the labels of the selected K entries
7. If regression, return the mean of the K labels
8. If classification, return the mode of the K labels
When to apply KNN
- Instances map to points in Rn
- Less than 20 attributes per instance
- Lots of training data
Advantages
- Training is very fast
- Learn complex target functions
- Can handle noisy data
- Does not loose any information
Disadvantages
- Slow at query time
- Easily fooled by irrelevant attributes
Clustering analysis or simply Clustering is basically an Unsupervised learning method that divides the data points into a number of specific batches or groups, such that the data points in the same groups have similar properties and data points in different groups have different properties in some sense. It comprises of many different methods based on different evolution.
E.g. K-Means (distance between points), Affinity propagation (graph distance), Mean-shift (distance between points), DBSCAN (distance between nearest points), Gaussian mixtures (Mahalanobis distance to centers), Spectral clustering (graph distance) etc.Fundamentally, all clustering methods use the same approach i.e. first we calculate similarities and then we use it to cluster the data points into groups or batches. Here we will focus on Density-based spatial clustering of applications with noise (DBSCAN) clustering method.
Clusters are dense regions in the data space, separated by regions of the lower density of points. The DBSCAN algorithm is based on this intuitive notion of “clusters” and “noise”. The key idea is that for each point of a cluster, the neighborhood of a given radius has to contain at least a minimum number of points.
DBSCAN
Partitioning methods (K-means, PAM clustering) and hierarchical clustering work for finding spherical-shaped clusters or convex clusters. In other words, they are suitable only for compact and well-separated clusters. Moreover, they are also severely affected by the presence of noise and outliers in the data.
Real life data may contain irregularities, like –
i) Clusters can be of arbitrary shape such as those shown in the figure below.
ii) Data may contain noise.
DBSCAN algorithm requires two parameters –
- Eps : It defines the neighborhood around a data point i.e. if the distance between two points is lower or equal to ‘eps’ then they are considered as neighbors. If the eps value is chosen too small then large part of the data will be considered as outliers. If it is chosen very large then the clusters will merge and majority of the data points will be in the same clusters. One way to find the eps value is based on the k-distance graph.
- MinPts: Minimum number of neighbors (data points) within eps radius. Larger the dataset, the larger value of MinPts must be chosen. As a general rule, the minimum MinPts can be derived from the number of dimensions D in the dataset as, MinPts >= D+1. The minimum value of MinPts must be chosen at least 3.
In this algorithm, we have 3 types of data points.
Core Point: A point is a core point if it has more than MinPts points within eps.
Border Point: A point which has fewer than MinPts within eps but it is in the neighbourhood of a core point.
Noise or outlier: A point which is not a core point or border point.
DBSCAN algorithm can be abstracted in the following steps –
- Find all the neighbor points within eps and identify the core points or visited with more than MinPts neighbors.
- For each core point if it is not already assigned to a cluster, create a new cluster.
- Find recursively all its density connected points and assign them to the same cluster as the core point.
A point a and b are said to be density connected if there exist a point c which has a sufficient number of points in its neighbors and both the points a and b are within the eps distance. This is a chaining process. So, if b is neighbor of c, c is neighbor of d, d is neighbor of e, which in turn is neighbor of a implies that b is neighbor of a. - Iterate through the remaining unvisited points in the dataset. Those points that do not belong to any cluster are noise.

References:
1. J. Shavlik and T. Dietterich (Ed), Readings in Machine Learning, Morgan Kaufmann, 1990.
2. P. Langley, Elements of Machine Learning, Morgan Kaufmann, 1995.
3. Understanding Machine Learning. Shai Shalev-Shwartz and Shai Ben-David. Cambridge University Press. 2017. [SS-2017]
4. The Elements of Statistical Learning. Trevor Hastie, Robert Tibshirani and Jerome Friedman. Second Edition. 2009. [TH-2009]