Unit - 5

Genetic Algorithms

5.1 Genetic Algorithms (GA)

GA’s are adaptive heuristic search algorithms inspired by evolutionary algorithms. Genetic algorithms are based on the ideas of natural selection and genetics. It uses intelligent exploitation of random search provided with historical data to direct the search into the region of better performance in solution space. 

GA is commonly used to generate high-quality solutions for optimization problems and search problems.

GA stimulates the natural selection process which means only species who can adapt to changes in their environment can survive and reproduce and pass on to the next generation.

In simple words, they follow the principle of “survival of the fittest” among individuals of consecutive generations for solving a problem.

Each generation consist of a population of individuals and each individual represents a point in search space and possible solution. Each individual is represented as a string of bits (character/integer/float). This string is analogous to the Chromosome.

Principle of Genetic Algorithm

Genetic algorithms are based on an analogy with the genetic structure and behavior of chromosomes of the population. Following is the foundation of GAs based on this analogy –

1. The individual in the population compete for resources and mate
2. Those individuals who are successful (fittest) then mate to create more offspring than others
3. Genes from “fittest” parent propagate throughout the generation, that is sometimes parents create offspring which is better than either parent.
4. Thus each successive generation is more suited for their environment.

Illustrative example

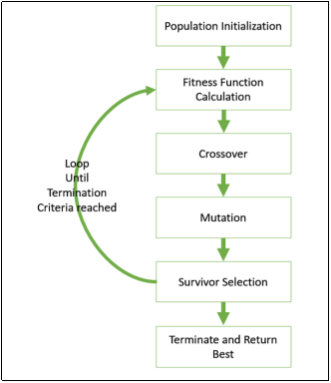
Figure. GA basic execution flow

GA(Fitness, Fitness_threshold,p,r,m)

Fitness: fitness function, Fitness_threshold: termination criterion,

p: number of hypotheses in the population, r: fraction to be replaced by crossover,

m: mutation rate

⇒ Initialize population: P ← Generate 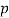hypotheses at random

⇒ Evaluate: For each 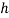in 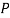, compute

⇒ While 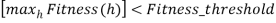, Do

1. Select: Probabilistically select 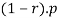members of 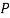to add to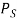
2. Crossover: Probabilistically select  pairs of hypotheses from 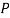. For each pair 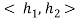produce two offspring and add to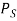
3. Mutate: Choose 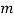percent of the members of with uniform probability. For each, invert one randomly selected bit
4. Update:
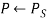
5. Evaluate: for each , compute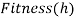

⇒ Return the hypothesis from 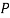that has the highest fitness.

5.1.1 Hypothesis space search

 The hypothesis method is not the same as other methods presented till far. It is neither general-to-specific nor simple-to-complex. Search is performed genetic algorithms takes place in a quick and undetermined way, replacing a parent hypothesis by an offspring which is radically different so this method is less likely to fall into some local minimum

Practical difficulty: crowding

 Some individuals that fit better than others reproduce quickly so that copies and very similar offspring take over a large fraction of the population ⇒ reduced diversity of population ⇒ slower progress of the genetic algorithms

Hypotheses are often represented as bit strings so that they can easily be modified by genetic operators. The represented hypotheses can be quite complex as each attribute can be represented as a substring with a no. Of positions. And as there are possible values to obtain a fixed-length bit string, each attribute has to be considered, even in the most general case.

Ex:

(Outlook = Overcast ∨ Rain ) ∧ (Wind = Strong ) is represented as: Outlook 011, Wind 10 ⇒ 01110

5.1.2Genetic Programming

Genetic programming (GP) is an evolutionary approach that exploits genetic algorithms to allow the exploration of the space of computer programs. GP works by defining a goal in the form of a quality criterion also known as fitness) and then using this criterion to evolve a set (or population) of candidate solutions by using the basic principles of Darwinian evolution. GP reproduces the solutions to problems using an iterative process involving the probabilistic selection of the fittest solutions and their variation through a set of genetic operators, usually crossover and mutation. GP has been successfully applied to some challenging real-world problem domains.

Its operations and behaviour are now reasonably well-understood thanks to a variety of powerful theoretical results

Advantages of GAs

GAs have various advantages that have made them immensely popular. These include −

• Does not require any derivative information (which may not be available for many real-world problems).
• Is faster and more efficient as compared to the traditional methods.
• Has very good parallel capabilities.
• Optimizes both continuous and discrete functions and also multi-objective problems.
• Provides a list of “good” solutions and not just a single solution.
• Always gets an answer to the problem, which gets better over time.
• Useful when the search space is very large and there are a large number of parameters involved.

Limitations of GAs

• Not suited for problems that are simple and for which derivative information is available.
• The fitness value is calculated repeatedly which might be computationally expensive for some problems.
• Being stochastic, there are no guarantees on the optimality or the quality of the solution.
• If not implemented properly, the GA may not converge to the optimal solution.

KEY TAKEAWAYS

• GA’s are adaptive heuristic search algorithms inspired by evolutionary algorithms. Genetic algorithms are based on the ideas of natural selection and genetics.
• Following is the foundation of GAs based on this analogy –

1. Individual in population compete for resources and mate

2. Those individuals who are successful (fittest) then mate to create more offspring than others

3. Genes from “fittest” parent propagate throughout the generation, that is sometimes parents create offspring which is better than either parent.

4. Thus each successive generation is more suited for their environment.

5.2 Models of Evolution and Learning

During an individual’s lifetime,  biological and social processes allow a species to adapt over a time frame of many generations, Individual organisms learn to adapt significantly.

5.2.1 Learning first-order rules-sequential covering algorithms

Propositional logic allows the expression of individual propositions and their truth-functional combination.

Ex: Ram is a man or All men are mortal can  be represented by single proposition letters P or Q– Truth functional combinations are built up using connectives, such as ∧, ∨, ¬, → – e.g. P∧Q

First-Order Logic:

All expressions in first-order logic are composed of the following attributes:  

1. Constants — e.g. Tyler, 23, a
2. Variables — e.g. A, B, C
3. Predicate symbols — e.g. Male, father (True or False values only)
4. Function symbols — e.g. Age (can take on any constant as a value)
5. Connectives — e.g. ∧, ∨, ¬, →, ←
6. Quantifiers — e.g. ∀, ∃

Term: It can be defined as any constant, variable, or function applied to any term. e.g. height(ram)

Literal: It can be defined as any predicate or negated predicate applied to any terms. e.g. Girl(sita), father(I, J)

It has 3 types:

• Ground Literal — a literal that contains no variables. e.g. Girl(sita)
• Positive Literal — a literal that does not contain a negated predicate. e.g. ) girl(sita) Negative Literal — a literal that contains a negated predicate. e.g. Father(X,Y)

First-order logic is much more expressive than propositional logic – i.e. it allows a finer-grain of specification and reasoning when representing knowledge

While in  machine learning, consider learning a relational concept daughter(x, y) defined over pairs of person x, y, where – persons are represented by attributes: (Name, Mother, Father, Male, Female)

5.2.2General to specific beam search-FOIL

FOIL learns first-order rules which are similar to Horn clauses with two exceptions:

• Literals may not contain function symbols (reduces the complexity of hypothesis space)
• Literals in body of clause may be negated (hence, more expressive than Horn clauses)

Like SEQUENTIAL-COVERING, FOIL learns one rule at a time and removes positive examples covered by the learned rule before attempting to learn a further rule.

Unlike SEQUENTIAL-COVERING and LEARN-ONE-RULE, FOIL

• Only tries to learn rules that predict when the target literal is true – propositional version
• Sought rules that predicted both true and false values of the target attribute
• Performs a simple hill-climbing search (beam search of width one)

FOIL searches its hypothesis space via two nested loops:

• The outer loop at each iteration adds a new rule to an overall disjunctive hypothesis (i.e. rule1 ∨ rule2 ∨...)

This loop may be viewed as a specific-to-general search

• Starting with the empty disjunctive hypothesis which covers no positive instances
• Stopping when the hypothesis is general enough to cover all positive examples

The inner loop works out the detail of each specific rule, adding conjunctive constraints to the rule precondition on each iteration.

This loop may be viewed as a general-to-specific search

• Starting with the most general precondition (empty)
• Stopping when the hypothesis is specific enough to exclude all negative examples

FOIL ALGORITHM

FOIL (Target_predicate, Predicates, Examples)

• Pos ← positive Examples
• Neg ← negative Examples
• Learned_rules ← {}
• While Pos, do

Learn a NewRule

-          NewRule ← most general rule possible (no preconditions)

-          NewRuleNeg ← Neg

-          while NewRuleNeg, do

Add a new literal to specialize NewRule

1. Candidate_literals ← generate candidates based on Predicates
2. Best_literal ←
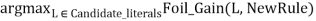
3. Add Best_literal to NewRule preconditions
4. NewRuleNeg ← subset of NewRuleNeg that satisfies NewRule preconditions

-          Learned_rules ← Learned_rules + NewRule

-          Pos ← Pos – {members of Pos covered by NewRule}

• Return Learned_rules

5.2.3REINFORCEMENT LEARNING - The Learning Task, Q Learning.

Reinforcement learning (RL) solves a particular kind of problem where decision making is sequential, and the goal is long-term, such as game playing, robotics, resource management, or logistics.

RL is an area of Machine Learning which is related to taking suitable action to maximize reward in a particular situation. It is employed by various software and machines to find the best possible behaviour or path. RL differs from supervised learning in a way that the training data has the answer key with it so the model is trained with the correct answer itself whereas in reinforcement learning, there is no answer but the reinforcement agent decides what to do to perform the given task. In the absence of a training dataset, it is bound to learn from its experience.

Example:

For a robot, an environment is a place where it has been put to use. Remember this robot is itself the agent. For example, a textile factory where a robot is used to move materials from one place to another.

These tasks have a property in common:

-  these tasks involve an environment and expect the agents to learn from that environment. This is where traditional machine learning fails and hence the need for reinforcement learning.

q-learning

Q-learning is another type of reinforcement learning algorithm that seeks to find the best action to take given the current state. It’s considered as the off-policy because the q-learning function learns from actions that are outside the current policy, such as taking random actions, and therefore a policy isn’t needed.

More specifically, q-learning seeks to learn a policy that maximizes the total reward.

Role of ‘Q’

The ‘q’ in q-learning stands for quality. Quality in this case represents how useful a given action is in gaining some future reward.

Create a q-table

When q-learning is performed we create what’s called a q-table or matrix that follows the shape of [state, action] and we initialize our values to zero. We then update and store our q-values after an episode. This q-table becomes a reference table for our agent to select the best action based on the q-value.

Updating the q-table

The updates occur after each step or action and end when an episode is done. Done in this case means reaching some terminal point by the agent. A terminal state for example can be anything like landing on a checkout page, reaching the end of some game, completing some desired objective, etc. The agent will not learn much after a single episode, but eventually, with enough exploring (steps and episodes) it will converge and learn the optimal q-values or q-star (Q∗).

Here are the 3 basic steps:

1. The agent starts in a state (s1) takes an action (a1) and receives a reward (r1)
2. The agent selects action by referencing Q-table with the highest value (max) OR by random (epsilon, ε)
3. Update q-values

Resources and links used

Great RL and q-learning example using the OpenAI Gym taxi environment

Reinforcement Learning: An Introduction (free book by Sutton)

Quora Q-learning

Wikipedia Q-learning

David Silver’s lectures on RL

R. S. Sutton, A. G. Barto: Reinforcement Learning: An Introduction. MIT Press, 1998

KEY TAKEAWAYS

• Lamarckian Evolution: proposition that evolution over many generations was directly influenced by the experiences of individual organisms.
• Baldwin Effect: a species in a changing environment underlies evolutionary pressure that favors individuals with the ability to learn.
• FOIL learns one rule at time and removes positive examples covered by the learned rule before attempting to learn a further rule.
• Reinforcement learning (RL) solves a particular kind of problem where decision making is sequential, and the goal is long-term, such as game playing, robotics, resource management, or logistics.

References:

1. Tom M. Mitchell, ―Machine Learning, McGraw-Hill Education (India) Private Limited, 2013.

2. Ethem Alpaydin, ―Introduction to Machine Learning (Adaptive Computation And Machine Learning), The MIT Press 2004.

3. Stephen Marsland, ―Machine Learning: An Algorithmic Perspective, CRC Press, 2009.

4. Bishop, C., Pattern Recognition, and Machine Learning. Berlin: Springer-Verlag.