UNIT 2

Plane Stress and Plane Strain Problems

2.1 Airy’s Stress Function

Airy stress function is a polynomial function which on differentiation gives stresses such that they always follow the two-dimensional equilibrium equation.

Plane stress problems-

Stress equilibrium equations for the plane-

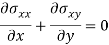
These equilibrium equations should be always followed by any 2D problem let us consider Q is a polynomial such that-

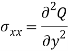
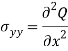
The above stresses also follow the equilibrium equation such a function Q is called Airy Stress Function.

We know the compatibility equation –

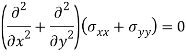
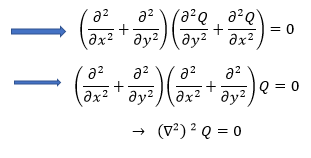
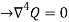
Because 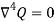, hence Q is a Bi- Harmonic Equation.

NOTE= Q is also called a polynomial solution.

2.2 Bi-Harmonic Equation

If a function (F) satisfy the following condition then that function will be called Bi-Harmonic Equation-

2.3 2D Problem on Airy space function

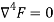
In this approach, we find a polynomial Q that satisfies the airy space function condition. After finding the Q we can get all 2D stresses using the following formula-

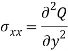
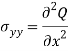
Example-A cantilevered beam subjected to a parabolic distribution of shear traction(τxy=λ[1-(y/d)^2]) as shown in the figure. The Airy stress function is given-

Q=C1xy+C2xy3+C3x2y2

Fig. 1 Cantilever  beam

Solution: we know    -

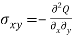
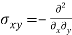                                     (C1xy+C2xy3+C3x2y2)

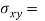C1+3C2y2+4C3xy

Comparing with given shear stress-

C1=-λ

C2=3λ/d2

C3=0

Putting the values of all C we will get Airy stress Function Q.

NOTE- To solve the problem using the Airy Stress function we follow the following steps-

1. Assume a general polynomial solution for Q.
2. The Q must be satisfy .
3. Satisfy the boundary conditions get the exact function Q.
4. By the definition, Q finds all the 2D desired Stresses.

Key Takeaway

1. Airy stress function-

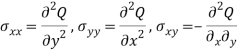
2.     Biharmonic equation-

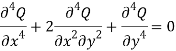
REFERENCES-

1. Book- Mechanics by Fridtjov  Irignes Chapter-7
2. Sadd 9.3, Timoshenko Chapter-11
3. Module 9 version 2 ME, IIT Kharagpur
4. Book- solid mechanics- 2nd by Kelly