UNIT 3
Polar coordinates
The equation of equilibrium in a plane can be written also in a polar coordinate system. Which will be very helpful to solve the circular problems are semi-infinite plate problem. We derived the equations by considering a differential element having stresses σrr, σƟƟ, σrƟ as shown in the following figure. The elemental radial size is Δr and rΔƟ and (r+ Δr) ΔƟ-
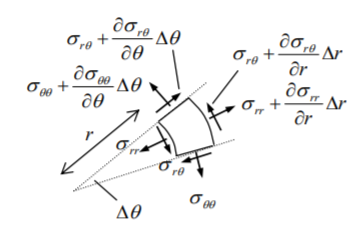
Figure 1 An element of material
On adding the radial forces-
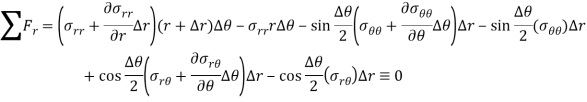
We know for a small element 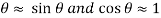 and dividing the whole equation by Δr, ΔƟ-
and dividing the whole equation by Δr, ΔƟ-
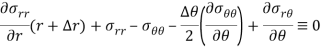
Similarly, on putting summation tangential direction forces equal to zero we will get the following two equilibrium equation in polar coordinates-
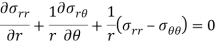
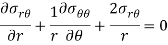
2D strain-displacement s relation equation in polar coordinate is given below-
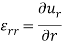
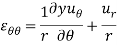
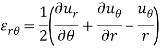
Stress-strain relation or Hook’s law in polar coordinate are given below-
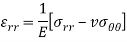
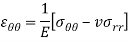
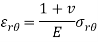
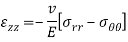

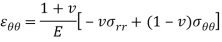
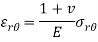
Airy stress function in polar coordinate can be driven from a general Cauchy equation of motion in polar coordinate by making acceleration and body forces zero. We get the equation of equilibrium the airy stress function in polar coordinate will be-
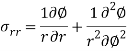
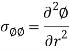
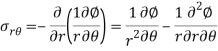
Biharmonic operator for polar coordinate equation-
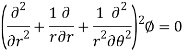
If a body is in a plane state of stress which is symmetrical with the z-axis, in such cases we can assume there will be only radial directional airy stress function exist. The general solution for such stresses the airy function will be-
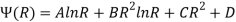
Where A, B, C, and D are constant for integration. For such cases, the coordinate stresses will be-

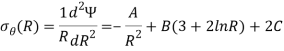
In axial symmetry cases, the shear stresses will be zero.
Figure 3.2 shows a curved beam with a rectangular cross-section with an inner radius a and outer radius b width t and thickness h(height)-
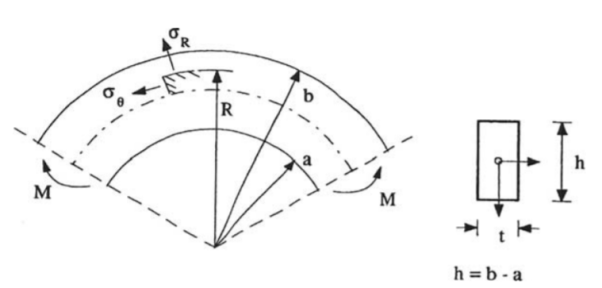
Figure 2- Curved Beam
The beam is subjected with a moment M then the boundary condition will be-
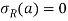
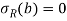
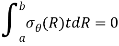
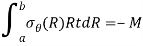
On substituting the above boundary condition in the general solution of axial symmetry function we will get three equation with the unknown constant A, B, C-

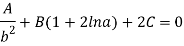
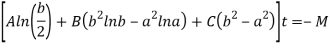
On solving the above three equation we will get the value of constants-
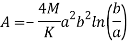
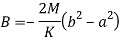
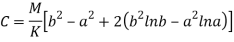
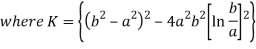
On putting the value of constant A, B, C we will get the stresses-
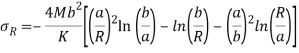
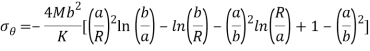
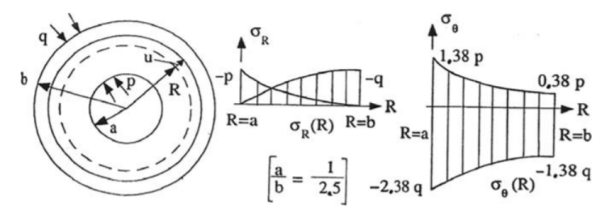
Figure 3- Circular disk with a hole
The axial symmetric general solution as discussed in 3.5 contains three unknown constants A, B, C. To get the value of these constants we have only two boundary condition in this problem-
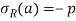
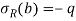
Hence here we conclude hook’s law and stress expression also –
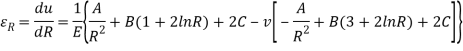
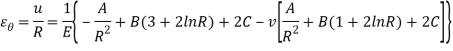
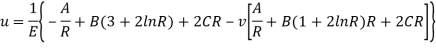
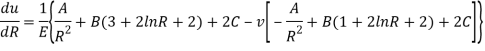
On comparing the above equation for du/dR we see that the value of B should be zero. Hence general expression for radial displacement and stresses for the above problem-
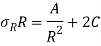
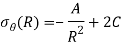
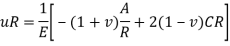
Now the general expression has only two unknown constant and two boundary condition also hence we can get the value of Constant A and C easily the final solution will be-
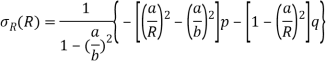
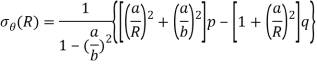
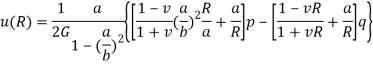
Stresses in solid rotating disk-
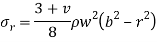
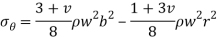
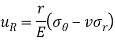
Where b is the outer radius of the disk and 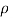 is the density of the material.
is the density of the material.
NOTE- their maximum stresses will be at the center r= 0
When the disk has a hole of radius a then the stresses will be-
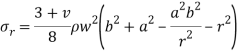
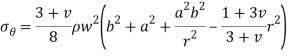
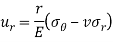
Where a is the radius of the hole and 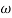 is angular velocity.
is angular velocity.
NOTE- 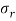 will be maximum at r=
will be maximum at r=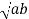 and
and 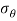 will be maximum at r=a.
will be maximum at r=a.
Edge load on a semi-infinite Elastic plate
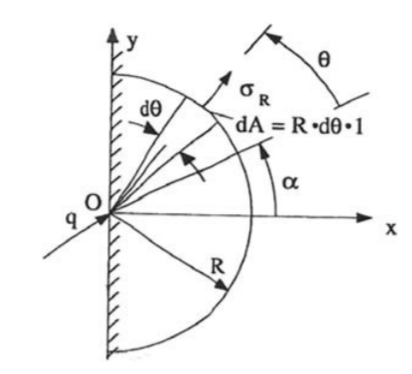
Figure 4- Semi-infinite Plate
The semi-infinite plate is defined as the region x>0 and having a load q per unit length in the z-direction. The polar stress function will be-
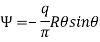
Ɵ is measured from the line of action on a load which is α wrt to positive x after applying biharmonic operator in above airy stress function we will see compatibility equation is satisfied. Now the coordinate stresses-
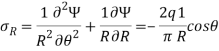
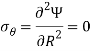
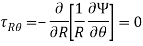
The boundary condition- t=0 on the surface x=0, in this case, we applied the equilibrium equation as a semi-cylinder having radius R and equating the forces we will get the value of q. Using this method this problem solve by Boussinesq in 1885.
Rectangular plate with a hole-
The rectangular plate is width height h, width v, and hole radius a << h,v, which is under the normal stress on x= b/2. And the sides y=
b/2. And the sides y= h/2 are free we find the stresses near the hole. As we know the points for away from the hole stresses will be like the plate without the hole.
h/2 are free we find the stresses near the hole. As we know the points for away from the hole stresses will be like the plate without the hole.
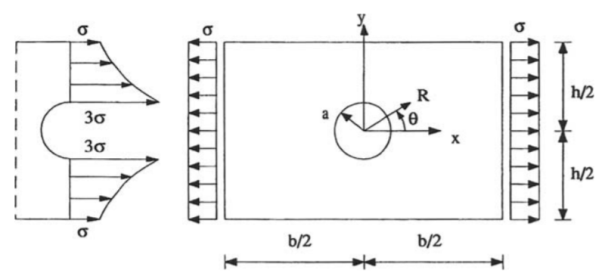
Figure 5- Plate with a small hole
The stress function which provides correct stresses near the hole is –
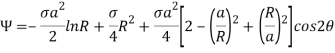
The above airy equation satisfied the compatibility hence the state of stress will be-
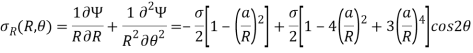
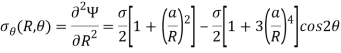
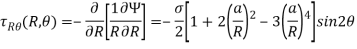
In this case, stresses at the hole – edge, R=a will be-
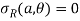
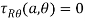
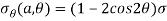
Key Takeaway
- Equilibrium equation in polar coordinates
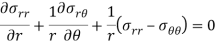
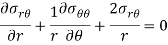
2. Airy Stress Function in the polar coordinate
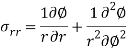
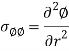
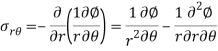
3. Biharmonic operator for polar coordinate equation
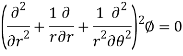
4. Stresses in the solid rotating disk
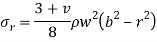
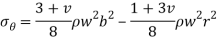
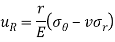
REFERENCES-
- Book- Mechanics by Fridtjov Irignes Chapter-7
- Sadd 9.3, Timoshenko Chapter-11
- Module 9 version 2 ME, IIT Kharagpur
- Book- solid mechanics- 2nd by Kelly