UNIT 4

TORSION

4.1 Navier’s Theory of Torsion

The equation of motion also called the Navier equation for plane stress are given below-

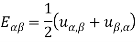
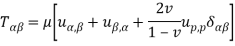
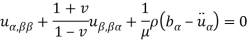
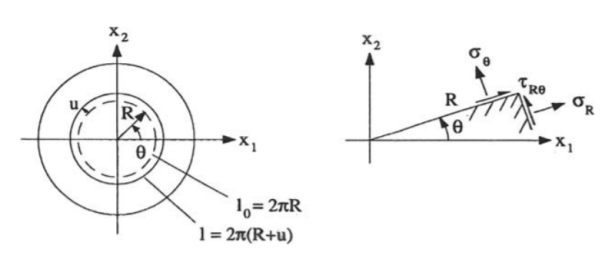
Figure 1 Circular plate with axis symmetrical displacement

Fig. 4.1 shows a circular slab having polar coordinate (R, Ɵ) it is axis symmetrical hence radial displacement will be a function of R only- u=u(R).

The area strain will be –

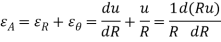
The Navier equation when xα is replaced by R-

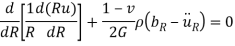
The stresses in polar coordinate are σR,τRƟ and σƟ  but here shear stress will be zero because of axis symmetry and by Hooke’s Law the remaining stresses will be-

4.2 St. Venant’s Theory of Torsion/Semi- inverse method

Figure.2 Torsion of Prismatic bar

Assumptions –

1. Each x3 =constant, rotation of the plane section like a rigid body about the center axis.
2. The rotation angle is a linear function of x3.

To derive a St. Venant principle of torsion we apply a semi-inverse method according to this- (for axis symmetrical circular lab)

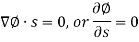
It shows stress function gradient is perpendicular to the tangent and parallel with the normal boundary of the cross-section. It means Ø is constant over the cross-section boundary. For boundary value problem-

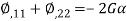
Ø=0

At the bar end (x3 =0, L), the internal stresses are used to balance the external forces.

Ignoring the details of how the external torque is applied-

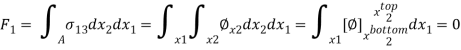
Similarly for F2(A is cross-sectional area)-

Here the Torque T should be –

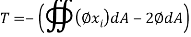
Where

First-term will be removed because Ø=0 at the boundary hence we get –

4.3 Application of St. Venant Theory/Semi-inverse method

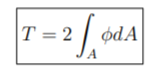
We use the following step to solve any bar having circular, elliptical, triangular, or rectangular cross-section-

1. By solving the Poisson equation with boundary conditions we get a stress function.
2. Obtain rate of twist from the equation

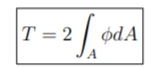
3.     Compute strain and stresses.

4.     Compute raping function

Example: Elliptical bar – A bar as shown in figure applied with a torque T at its end and the boundary condition is given below

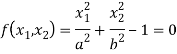
Find a stress function Ø

Solution: let us consider Ø= K f(x1,x2) where K is constant and function is associated with boundary function. Then-

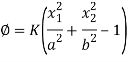
By governing equation –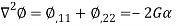

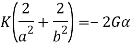
K= -G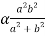

Now the torque-

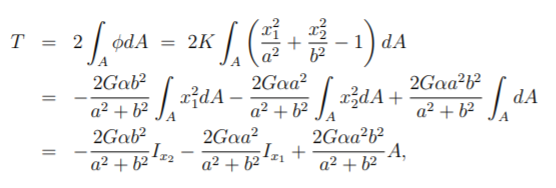
Where moment of inertia-

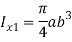
A= πab (area 0f cross section)

Replacing it we get-

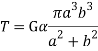
The new Ø will be-

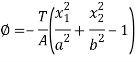
Now by using stress eqn.-

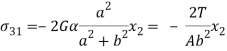
Above eqn. Are the solution to the problem.

4.4 Prandtl’s Theory on Torsion

We can use an alternative way to solve the torsion problem using Prandtl’s stress function-(Ω(x,y))-

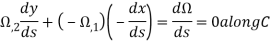
Where C is contour. Using Gauss theorem in the plane-

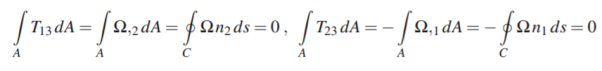
Using boundary condition-

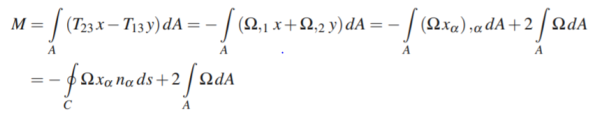
First-term is zero hence –

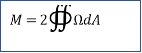
Using boundary condition, the Prandtl function should satisfy the following condition also –

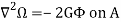
Note- The previous elliptical cross-sectional problem can be solved using this theorem also. The result will be the same

4.5 Membrane Analogy

There are many cross-sections for which to find an analytical solution is very tough hance for these type of problem in 1903 Prandtl include an analogy which called membrane analogy in this analogy we take a thin membrane from the cross-section which have uniform pressure load as shown in figure-

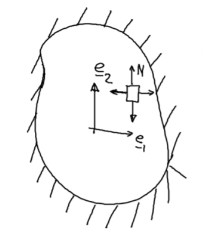
Figure 3 shows the membrane subjected to a uniform pressure

If N is membrane force per unit length and P is uniform pressure then normal deflection will be –

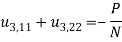
Here the boundary condition will be u3(x1, x2 )=0, On comparing here we can get an analogy between membrane and torsion problem –

Membrane	Torsion
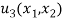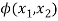p/N	2Gα
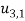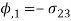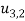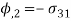V=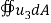

Using the above analogy we can convert a complex membrane problem into a simple problem.

Key Takeaway:

1. Navier’s Theory of Torsion

2.     Venant’s Theory of Torsion

3.     Prandtl’s Theory on Torsion

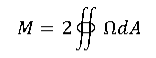
4.     Membrane Analogy

Membrane	Torsion
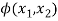p/N	2Gα
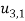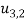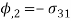V=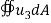

REFERENCES-

1. Book- Mechanics by Fridtjov  Irignes Chapter-7
2. Sadd 9.3, Timoshenko Chapter-11
3. Module 9 version 2 ME, IIT Kharagpur
4. Book- solid mechanics- 2nd by Kelly