UNIT 5

Introduction to Theory of Plates and Shells

5.1 Classical Plate theory (KCPT)

Assumptions-

●       Thickness is smaller than the other dimension.

●       Displacements are much smaller than plate thickness.

●       Governing equations are based on undeformed geometry.

●       Materials follow Hook’s Law.

●       The middle surface is always unstrained during bending.

●       The Plane normal to the middle surface remains normal.

●       Rotatory inertia is negligible. Transverse shear strains also negligible.

Let us consider a thin plate in xy plane as given in the figure-

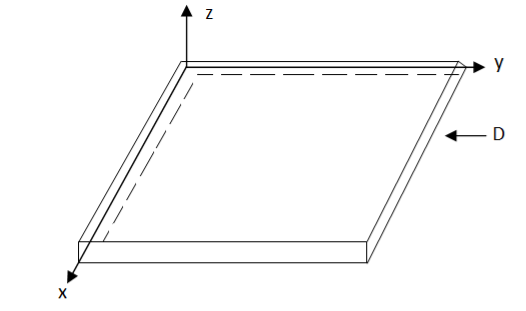
Figure 1 A thin plate

Moments-

Moment wrt to y-axis- let us consider a cubical small element as shown in figure we will get

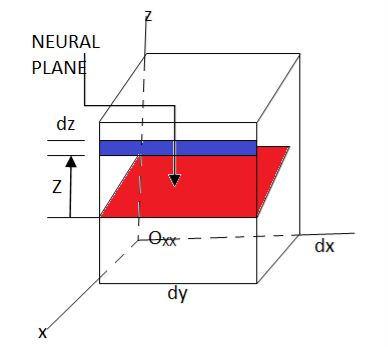
Figure 2 Small differential element

DFxx  =σxx dz

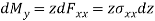
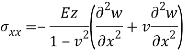
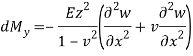
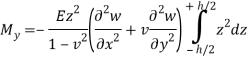
Moment wrt to x-axis- (similarly)-

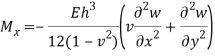
Twisting moment of shear stress

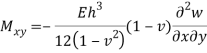
Using the section module formula of the beam –

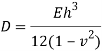
Shear  forces

Vertical equilibrium of plate-

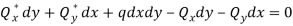
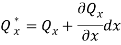
Substituting the above equation we get-

Shear force according to thickness-

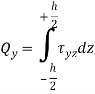
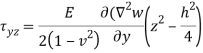
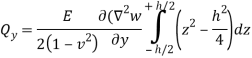
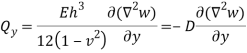
Governing Equation

For Qx –

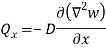
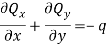
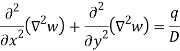
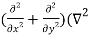w) =

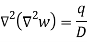
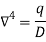
Bi-harmonic governing equation

5.2 Boundary Conditions

There are three possibilities of boundary condition-

1. Simply supported-

Figure 3- Middle plane

For x constant –

w( x , y ) = 0

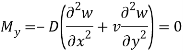
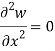
For edge y constant-

W=0

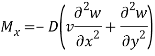
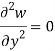
2.     Clamped-

For x constant –

W=0

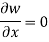
For y constant-

W=0

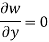
3.     Free edge-

For x constant-

Bending moment-

Moment xy and shear –

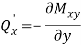
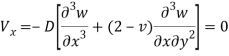
For y constant-

Bending moment-

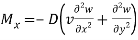=0

Shear force-

5.3 Navier’s method for a simply supported rectangular plate

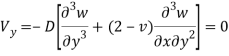
Navier solution for lateral deflection of a simply supported rectangular plate having dimension a and b with distributed q as shown in the figure-

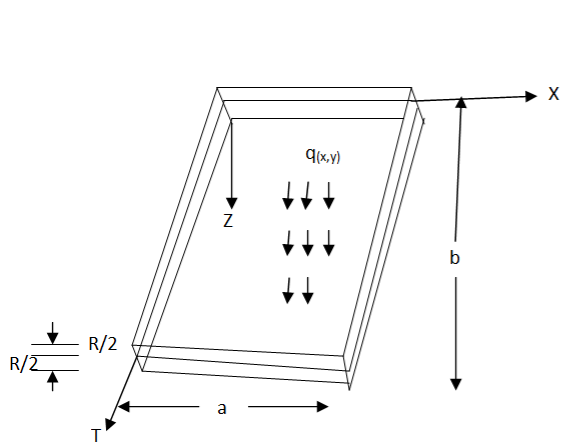
Figure 4- Simply supported plate

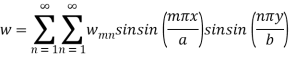
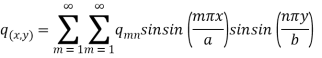
Where m, n=1,3,5……

Multiply both side by sin(jπx/a) sin(kπy/b) and integrate wrt x and y from 0 to a

And 0 to b-

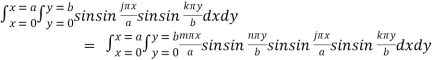……(1)

Integrating wrt x-

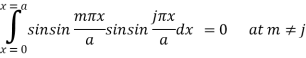
Integrating wrt y-

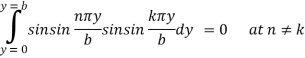
At m = j

=

Similarly at n=k –

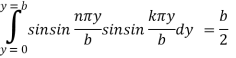
Now the equation(1) will be –

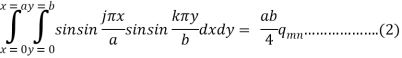
Substituting w and q(x,y) in the fourth-order governing differential equation-

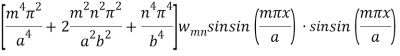
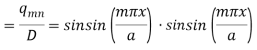
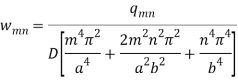
Now the W-

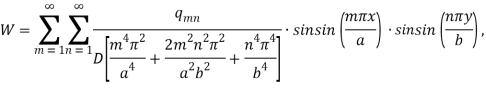
Integrating equation (2) wrt x and y-

And

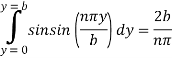
Substituting the above two values in the equation number (2) we will get-

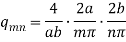
Now the equation (1) will be –

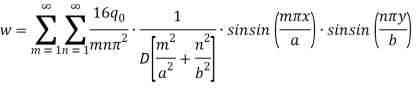
This is the equation of deflection for UDL using the Navier method for method.

5.4 Levy’s Method of Solution for Rectangular Plates

Let us consider a thin plate in xy plane in which at y=0 and y=b are simply supported and at x=0 and x=a can have any support like(clapped, free or simply supported) as shown in the figure –

Figure 5- Neutral plane of thin plate

A suitable governing equation for this case will be-

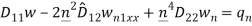
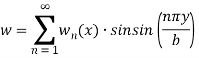
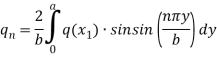
For an isotropic plate-

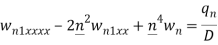
Let us consider this is a square plate a=b=1m, n=1 made of steel and n=1 then-

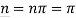
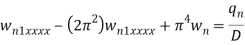
Because it is a differential equation of fourth-order. Hence it will give two solution-

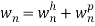
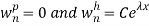
Where λ is the roots of the equation.

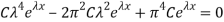
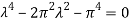
If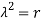

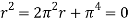
For isotropic plate  r12 = π2, now the roots will be-

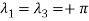
And

The solution-

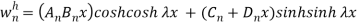
And

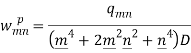
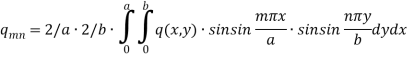
The final solution will be-

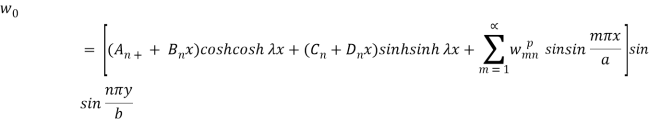
The above equation is the solution for the plate using the Levy theorem.

Key Takeaway:

1. KCPT
2. 
3. 
4. 
5. 

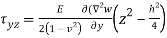
6.     Navier Method For plate (deflection)

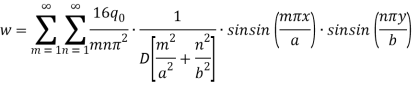
7.     Levy theorem For plate

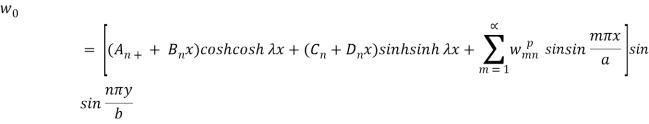
REFERENCES-

1. Book- Mechanics by Fridtjov  Irignes Chapter-7
2. Sadd 9.3, Timoshenko Chapter-11
3. Module 9 version 2 ME, IIT Kharagpur
4. Book- solid mechanics- 2nd by Kelly