UNIT 2
Equilibrium
To apply the equation of equilibrium, we have to consider all types of forces (ΣF) which are acting on the particle. A drawing in which all the forces are depicted is called free body diagram (FBD).
Process to Draw a Free-Body Diagram
To construct a free body diagram, the following three steps are necessary.
Imagine that the particle is to be isolated from its environments by drawing its outlined shape.
b. Show All the forces.
Then on this sketch, show all the types of forces. Identify Each Force that are known and unknown and display them.
c. Identify each force
Known forces are displayed with magnitude and direction. Letters are used to represent the magnitudes and directions of forces that are unknown.
For understanding the free-body diagram, we will consider the following example:
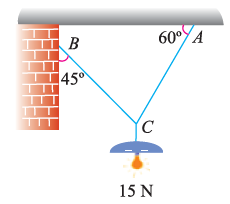
Suppose, in this example there are two strings (AC and BC) attached to an object at point C. Thus, the first step involves drawing a simple diagram representing the outline of all components.
Then, we need to show all the forces that are contributing in the given diagram. Here, there is 15 N force acting at point C, and there is tension in strings BC and AC due to 15 N force acting at C. Thus, identifying and displaying these forces onto the outline diagram is the second step.
The third step is finding the magnitude and direction of the forces and displaying them on the outline diagram. Using these steps, we can draw the free-body diagram as shown below.
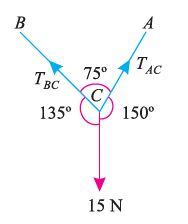
1. If the body moves in any direction, it means that there is a resultant force acting on it. In other words, the horizontal component of all the forces (Σ H) and vertical component of all the forces (ΣV) must be zero. Mathematically,
Σ H = 0 and Σ V = 0
2. If there is rotation of body, without moving, that means there is couple acting. In other words, the resultant moment of all the forces (Σ M) must be zero. Mathematically,
Σ M = 0
3. If the body moves in any direction and at the same time it rotates about itself, if means that there is a resultant force and also a resultant couple acting on it. In other words, horizontal component of all the forces (Σ H), vertical component of all the forces (Σ V) and resultant moment of all the forces (Σ M) must be zero. Mathematically,
Σ H = 0 Σ V = 0 and Σ M = 0
4. If the body is completely at rest it means there is no force nor any couple acting on it. A little consideration will show, that in this case the following conditions are already satisfied:
Σ H = 0 Σ V = 0 and Σ M = 0
The above-mentioned equations are known as the conditions/equations of equilibrium.
Thus, the equations of equilibrium for two-dimensional coplanar force system are given by considering that the particle is present in x-y plane as shown in fig. below, then the force can be resolved into i and j components.

For equilibrium, the forces must add on to produce a zero-force output, i.e.,
Σ F = 0
Σ Fx i + Σ Fy j = 0
Thus, for satisfying this vector equation, the x and y component must be zero as mentioned in earlier points. Hence,
Σ Fx = 0
Σ Fy = 0
Thus, for solving two-dimensional coplanar force problems using conditions of equilibrium, we can follow the below-mentioned procedure.
Free-Body Diagram.
• In any orientation, establish x and y axes.
• Then mark all the known and unknown forces in figure.
• Unknown forces are also assumed and plotted.
Equilibrium equation.
• Apply the equations of equilibrium, Σ Fx = 0 and Σ Fy = 0.
• The forces are directed as positive for those along positive axis and vice-versa.
• If the resultant comes out to be negative value, it means that the direction needs to be reversed for that is already considered.
As we know, the sufficient case for stating equilibrium for a body under combination of forces is Σ F = 0.
For any three-dimensional force system, as shown in Fig. below, we can resolve the forces into their respective i, j, k components, so that
Σ Fx i + Σ Fy j + Σ Fz k = 0
To satisfy this equation we require,
Σ Fx = 0
Σ Fy = 0
Σ Fz = 0
These three equations state that the algebraic sum of the components of all the forces acting on the particle along each of the coordinate axes must be zero. Using these equations mentioned we can solve for maximum three of the unknowns, shown by coordinate direction angles or magnitudes of forces shown on the particle’s free-body diagram.
For solving three-dimensional problem, we can use the following procedure.
Free Body Diagram:
• In any orientation, establish x and y axes.
• Then mark all the known and unknown forces in figure.
• Unknown forces are also assumed and plotted.
Equations of Equilibrium.
• Apply the equations of equilibrium, Σ Fx = 0, Σ Fy = 0 and Σ Fz = 0.
• Initially we can display as a Cartesian vector if it becomes to solve the problem regularly, substitute these vectors into Σ F = 0 and then set the i, j, k components equal to zero.
• If the resultant comes out to be negative value, it means that the direction needs to be reversed for that is already considered.
The above-mentioned procedure (2.2) is used for finding solutions to two- and three-dimensional problems. This procedure can be better understood through some of the examples mentioned below.
e.g. 1: Determine the tension that will be there in cables BA and BC necessary to support the 60-kg cylinder in Fig. below.
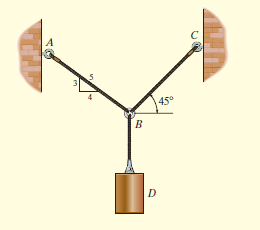
Solution:
The first step involves drawing the free-body diagram of the given example. As this is two-dimensional structure, we will follow the method mentioned for two-dimensional coplanar structure.
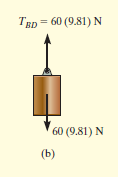

2. Equations of Equilibrium: Applying the equations of equilibrium along the x and y axes, we have
Σ Fx = 0 i.e. TC cos 45° - (4/5)TA = 0
Σ Fy = 0 i.e. TC sin 45° + (3/5)TA - 60(9.81) N = 0
Solving the above equations, we get, TC = 475.66 N = 476 N
Then, substituting this value in above equation,
TA = 420 N
In this way, using the equilibrium equations, we can solve for the unknown force in the given problem.
e.g. 2: The 200-kg crate in Fig. below is suspended using the ropes AB and AC . Each rope can withstand a maximum force of 10 kN before it breaks. If AB always remains horizontal, determine the smallest angle to which the crate can be suspended before one of the ropes breaks.
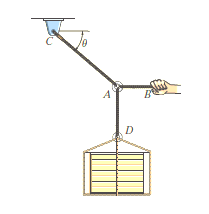
Solution:
Free-Body Diagram: We will initially understand the equilibrium of ring. There are three forces acting on it, as shown in fig. (b). The magnitude of is equal to the weight of the crate, i.e.,
FD = 200 (9.81) N = 1962 N < 10 kN

Equations of Equilibrium: Applying the equations of equilibrium along the x and y axes,
i.e. - FC cos θ + FB = 0
Therefore FC = ( FB / cos θ )
Σ Fy = 0
i.e. FC sin θ - 1962 N = 0
As seen from the above equations, FC is always greater than FB as cos θ is less than or equal to 1. So, rope AC will reach the max value of tensile force of 10 kN before that of rope AB. Thus, substituting FC = 10 kN in the above equations, we get
[10(103) N] sin θ - 1962 N = 0
Thus, θ = 11.30
The force developed in rope AB can be obtained by substituting the values for θ and FC into Equations mentioned above.
We get, FB = 9.81 kN.
In this way, using equations of equilibrium and free-body diagrams, we can calculate unknown quantities of the given problem.
Problems in Three-dimensions:
e.g. 3: The 10-kg lamp in Fig. below is suspended from the three equal-length cords. Find the smallest vertical distance s from the ceiling if force built in cord is not to go beyond 50 kN.
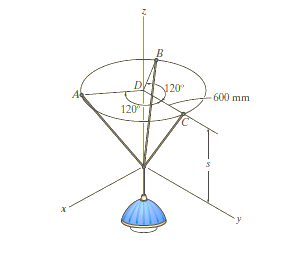
Solution:
For solving these three-dimensional numerical, we will follow the same procedure mentioned above.
Free-Body Diagram: Because of symmetry, the distances are as  mm. It follows that from Σ Fx = 0 and Σ Fy = 0, the tension T in each cord will be the same. Also, the angle between z axis and every cord is
mm. It follows that from Σ Fx = 0 and Σ Fy = 0, the tension T in each cord will be the same. Also, the angle between z axis and every cord is 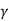 .
.
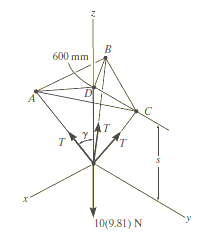
Equation of Equilibrium: Applying the equilibrium equation along the z-axis, with T = 50 N, we have
Σ Fz = 0;
3[(50 N) cos  ] - 10(9.81) N = 0
] - 10(9.81) N = 0
 = cos-1 (98.1 / 150)
= cos-1 (98.1 / 150)
= 49.160
Now,
By geometry shown in free-body diagram,
tan 49.160 = (600 / s)
s = 519 mm
In this way, three-dimensional problems are solved using equations of equilibrium.
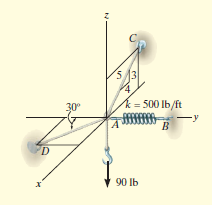
e.g. 4: A 90-lb load is being suspended from a hook as shown in Fig. below. If the load is being supported by two cables and a spring having a stiffness of k = 500 lb/ft, find the force in the cables and the stretch of the spring for equilibrium. Cable AD lies in the x–y plane and cable AC lies in the x–z plane.
Solution:
Initially, force in spring is determined to determine stretching of spring.
Free-Body Diagram. A point is chosen for all analysis as all the points are concurrent here. The free-body diagram for the problem is shown in Fig. below.
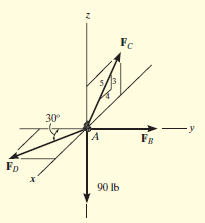
Equations of Equilibrium. We can resolve each force in x, y and z components, and so we can use three scalar equations of equilibrium. Considering components directed along each positive axis as “positive,” we have
Σ Fx = 0
FD sin 30° - (4/5) FC = 0
Σ Fy = 0
-FD cos 30° + FB = 0
Σ Fz = 0
(3/5) FC – 90 lb = 0
Thus, solving the above-mentioned equations, we get,
FC = 150 lb
FD = 240 lb
FB = 207.8 lb
The stretch of the spring is therefore
FB = ksAB
207.8 lb = (500 lb/ft) (sAB)
sAB = 0.416 ft
Thus, the method discussed earlier can be followed as shown in the examples for finding out the unknown quantities in two- and three-dimensional problems using equations of equilibrium.
Truss:
A truss is a structure which is made of slender members those are joined together at the end points. Planar trusses lie in one single plane and these are frequently used to support some of the bridges and roofs. Fig. (a) is a typical roof-supporting truss used for construction. Since this loading turns in the similar plane as the truss, Fig. (b), the analysis of the forces developed in the truss members will be two-dimensional.


Simple truss problems can be solved using two methods:
For solving simple truss example using method of joints we will follow the below procedure.
Draw the free body diagram which minimum one known and 2 unknown force.
Use one of the two methods described above for establishing the sense of an unknown force.
Draw x and y axed such that we can easily solve for x and y components and then apply the two force equilibrium equations and Solve for the two unknown member forces and verify their correct sense.
For solving simple truss example using method of sections we will follow the below procedure.
Make a cut in section where forces are to be determined.
Initially determine support reactions.
Draw the free-body diagram of that segment of this type of truss which is sectioned with minimum forces.
Unknown member forces can be found by above mentioned methods.
Moments should be summed about a point that lies at the intersection of the lines of action of two unknown forces, so that the third unknown force can be determined directly from the moment equation.
If two of the unknown forces are parallel, forces may be summed perpendicular to the direction of these unknowns to determine directly the third unknown force.
Plane Frame:
Frames are the type of structures which are often composed of pin-connected multiforce members, i.e., members that are subjected to more than two forces. Frames are used to support loads.
The process for solving problems of plane frames is as discussed below.
Draw the free-body diagram of the entire frame or machine, a portion of it, or each of its members. The choice should be made so that it leads to the most direct solution of the problem.
When the free-body diagram of a group of members of a frame or machine is drawn, the forces between the connected parts of this group are internal forces and are not shown on the free-body diagram of the group.
Forces common to two members which are in contact act with equal magnitude but opposite sense on the respective free-body diagrams of the members.
Two-force members, regardless of their shape, have equal but opposite collinear forces acting at the ends of the member.
In many cases it is possible to tell by inspection the proper sense of the unknown forces acting on a member; however, if this seems difficult, the sense can be assumed.
Remember that a couple moment is a free vector and can act at any point on the free-body diagram. Also, a force is a sliding vector and can act at any point along its line of action.
Count the number of unknowns and compare it to the total number of equilibrium equations that are available. In two dimensions, there are three equilibrium equations that can be written for each member.
Sum moments about a point that lies at the intersection of the lines of action of as many of the unknown forces as possible.
If the solution of a force or couple moment magnitude is found to be negative, it means the sense of the force is the reverse of that shown on the free-body diagram.