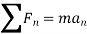UNIT 4
Dynamics
Kinematics is the branch of mechanics or simply a part of dynamic analysis which deals with the study or analysis of the motion of the body without considering the forces that causes this motion.
Hence Kinematics only analyses the geometry of the particle or rigid body.
2. Kinetics
Kinetics is the branch of mechanics or simply a part of dynamic analysis which deals with the study of motion of the body by considering the forces that causes this motion.
In other words, kinematics relates with the forces acting on the moving body.
Dynamics can be also classified on the basis of the body under study.
Particle is nothing but a point body or a body who does not have any size and shape. Analysis of a particle in motion is referred to as particle dynamics
2. Rigid body dynamics
Rigid body is a body who does not change its shape and size when subjected to various forces and couples. Analysis of rigid body is referred to as rigid body dynamics
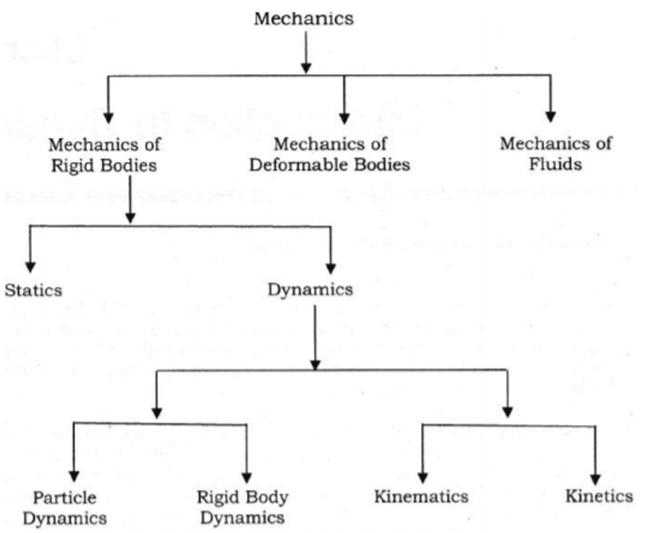
Consider a particle in a motion along the path ‘s’ shown in the figure below;

The motion of the particle can be best expressed in terms of x, y and z coordinates.
Consider the particle is at the point P (x, y, z) on the curve s as shown in fig above. The position of the particle is defined by the position vector r.
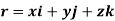
Where, x, y and z are the instantaneous coordinates of the position of particle in motion.
As the particle is in motion, the x, y, z components of r are the function of time.
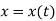
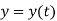

Hence,
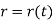
The instantaneous magnitude of the position vector is given by

And the direction of position vector is given by the unit vector
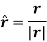
The instantaneous velocity of the particle can be defined by the first derivative of the position vector w.r.t time t

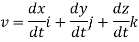
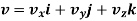
This is the velocity vector
Where, 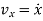 ,
, 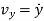 and
and 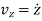 .
.
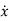 ,
,  and
and  represents the first derivative of
represents the first derivative of  ,
,  and
and  respectively.
respectively.
The instantaneous magnitude of the velocity can be given as

And the direction of velocity vector is given by the unit vector

Note: The velocity vector is always directed tangent to the path
The acceleration of the particle can be found by first derivative of the velocity vector or second derivative of position vector.
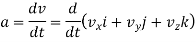
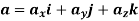
This is the acceleration vector
Where,
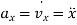

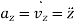
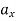 ,
,  and
and  represents the first time derivative of
represents the first time derivative of  ,
, 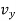 and
and  (i.e.
(i.e.  ,
, 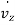 and
and  ) respectively. Also,
) respectively. Also, 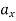 ,
,  and
and  represents the second time derivative of x, y and z (i.e.
represents the second time derivative of x, y and z (i.e. 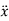 ,
,  and
and 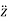 ) respectively.
) respectively.
The instantaneous magnitude of the acceleration can be given as
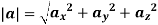
And the direction of velocity vector is given by the unit vector

Note: Curvilinear motion can cause changes in both the magnitude and direction of the position, velocity and acceleration vectors.
If the motion of the particle is constrained to a plane then the polar coordinate system is used for the kinematic study. And if the study is 3D, then cylindrical coordinate system is used.
In polar coordinate system, the position of the particle is defined by r and 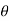
Where r is radial coordinate that represents the radial distance and 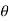 is the transverse coordinate that represents angle. The directions of the r and
is the transverse coordinate that represents angle. The directions of the r and 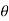 coordinates are defined by unit vectors
coordinates are defined by unit vectors 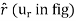 and
and 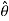
 respectively.
respectively.
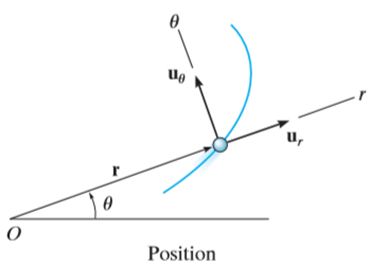
The location of particle at any instant is given by the position vector.
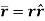
Velocity is given by velocity vector found by first derivative of position vector,

But,

Hence,


Where,
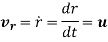
Where, u is the linear instantaneous velocity
And

Where, 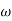 is the angular velocity
is the angular velocity
 is the radial velocity which is due to the change in the displacement or position of the particle.
is the radial velocity which is due to the change in the displacement or position of the particle.
And 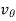 is the transverse velocity which is due to the change in direction of the particle.
is the transverse velocity which is due to the change in direction of the particle.
Hence, resultant velocity is given by,

The magnitude of the resultant velocity is given by
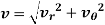

Acceleration of the particle can be found by first derivative of velocity vector

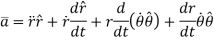
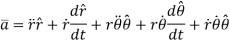
But,
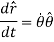
And

Hence,
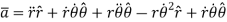


Where,
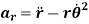
And
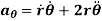
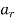 is the radial acceleration which is due to the change in the magnitude of velocity of the particle.
is the radial acceleration which is due to the change in the magnitude of velocity of the particle.
And  is the transverse acceleration which is due to the change in direction of velocity of the particle.
is the transverse acceleration which is due to the change in direction of velocity of the particle.
The magnitude of resultant acceleration is given by,
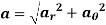

If the particle moves in a 3D space as shown in the figure below, then the location and motion of particle requires three cylindrical coordinates out of which two coordinates are same as of polar coordinate (viz. 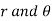 ). Additional third coordinate ‘
). Additional third coordinate ‘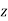 ’ is required which is identical to coordinate used in rectangular coordinates.
’ is required which is identical to coordinate used in rectangular coordinates.

The directions of the r, 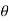 and
and  coordinates are defined by unit vectors
coordinates are defined by unit vectors  ,
, 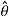
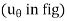 and
and 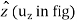 respectively.
respectively.
The position vector in cylindrical system is given by,
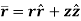
The velocity vector in cylindrical system is given by,

The velocity vector in cylindrical system is given by,
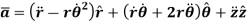
When the path of a particle motion is known, then the motion is best described by n and t coordinate axes that acts normal and tangent to the path of motion of the particle respectively. The origin is considered at the location of particle.
Consider the particle as shown in Figure below.
The particle moves in a plane along a fixed curve.
In n-t coordinate system origin is always at the location of the particle.
The t-axis is tangent to the path at the instant in positive direction of the particle’s motion.
The n-axis is perpendicular to the t-axis with the positive direction toward the center of curvature of the curve which is always on the concave side of the curve or path.
The directions of normal and tangent are defined by the unit vectors 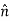
 and
and 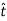
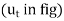
The position of particle is defined by the distance ‘s’ of the particle from the point O which is fixed on the curve. Generally, it is the start point of the path of particle motion.
S is a function of time and called as path function.
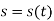
The velocity vector is always tangent to the curve and is given by
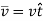
The magnitude of velocity is given by
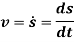

The acceleration of the particle is the time rate of change of the velocity. Thus,
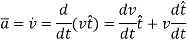
And

Hence,
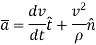

Where,
 is the tangential component of acceleration while
is the tangential component of acceleration while 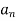 is normal component of acceleration? And both are given by,
is normal component of acceleration? And both are given by,

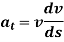
And

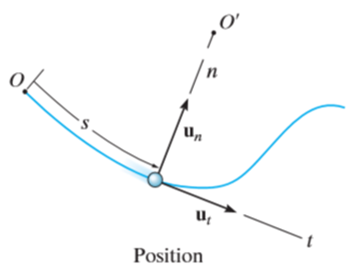
Where, 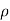 is the radius of curvature.
is the radius of curvature.
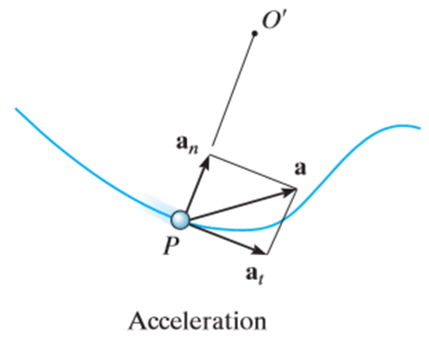
These two mutually perpendicular components of acceleration are shown in Figure above. Therefore, the magnitude of acceleration is given by,
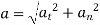
A particle moving along the curved path as shown in Figure below will have accelerations as directed in the figure.

Newton’s second law is the basis for kinetics. It states that when an unbalanced force acts on a particle, the particle will accelerate in the direction of the force with a magnitude that is proportional to the force.
If the mass of the particle is m, Newton’s second law of motion can be given in mathematical form as

When more than one force acts on a particle, the resultant force is defined by a vector summation of all the forces.
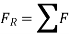
In general equation of motion is written as,
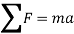
Consider the particle shown in Figure below.
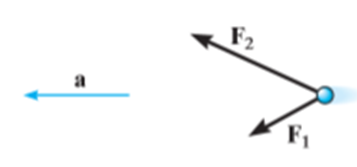
The particle has a mass m. It is subjected to two forces  and
and 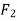 .
.
We can graphically give for the magnitude and direction of every force acting on the particle by the free-body diagram of the particle. As the resultant of these forces gives the vector ‘ma’, its magnitude and direction may be shown graphically on the kinetic diagram as shown below.

Inertial Reference Frame: When applying the equation of motion, it is important that the acceleration of the particle be measured with respect to a reference frame that is either fixed or translates with a constant velocity. In this way, the observer will not accelerate and measurements of the particle’s acceleration will be the same from any reference of this type. Such a frame of reference is commonly known as a Newtonian or inertial reference frame.
Equation of motion for a system of particles:
At the instant, consider the arbitrary ith particle which have a mass of 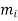 . Let it is subjected to a system of internal forces and a resultant external force.
. Let it is subjected to a system of internal forces and a resultant external force.
Internal forces are represented by 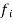 and these are the resultant of all the forces the other particles exert on the ith particle
and these are the resultant of all the forces the other particles exert on the ith particle
External forces are represented by 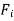 and these are the gravitational, electrical, magnetic or contact forces between the ith particle and adjacent bodies or particles that are not included within the system.
and these are the gravitational, electrical, magnetic or contact forces between the ith particle and adjacent bodies or particles that are not included within the system.
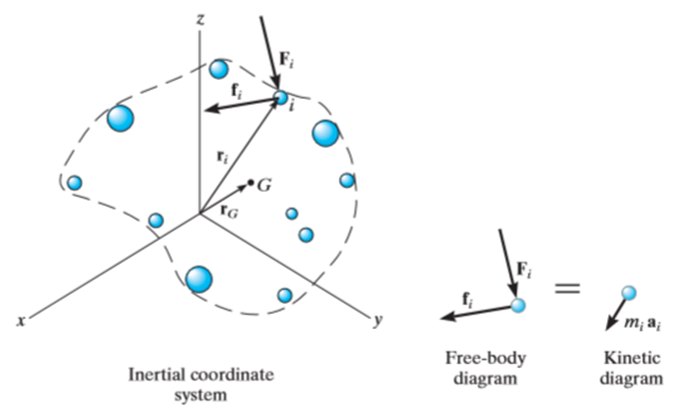
The equation of motion will be given by
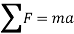
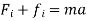
When the equation of motion is applied to each of the other particles of the system and all these equations are added together, we get
When a particle is in motion and the inertial frame of reference is an x, y, z coordinate system, the forces acting on the particle and its acceleration is given in terms of their i, j, k components
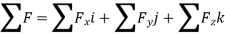
And

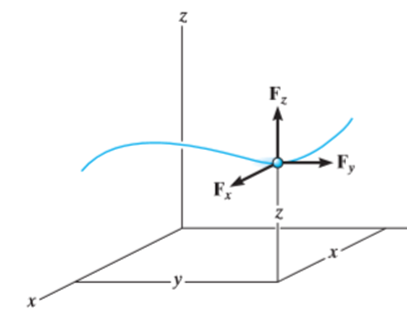
Applying equation of motion
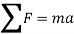

In scalar form,


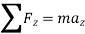
When all the forces acting and accelerations of a particle are resolved into cylindrical components, the unit vectors in the r, 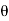 , z inertial frame of reference along r,
, z inertial frame of reference along r,  and z coordinates are given by,
and z coordinates are given by, 
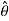
 and
and 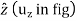 respectively.
respectively.
The forces acting on the particle and its acceleration is given by
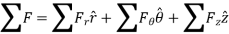
And

Applying equation of motion

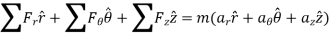
In Scalar form,


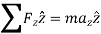
When a particle is in motion along a curved path which is known, then equation of motion for the particle is written in the tangential (t), normal (n), and binormal (b) directions. The direction of t, n and b coordinates is given by the unit vectors 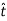 (
(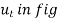 ),
), 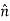 (
(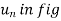 ) and
) and 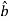 (
(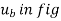 ). In this case, the inertial frame of reference may be taken t, n, b coordinate system.
). In this case, the inertial frame of reference may be taken t, n, b coordinate system.
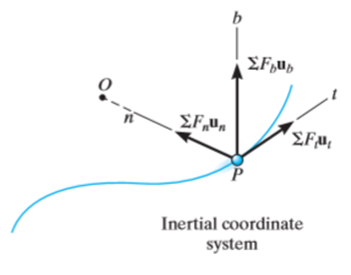
Here, there will be no motion in binormal direction as the particle moves along the fixed known path, but force may act in binormal direction.
The force and acceleration can be given as,
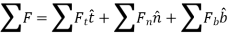
And,

Hence, applying equation of motion,
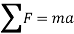

In scalar form,
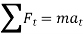
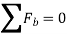
As we know, 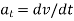 , it represents the time rate of change of magnitude of velocity. So if
, it represents the time rate of change of magnitude of velocity. So if 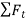 is in the direction of motion, the particle will accelerate or the speed will increase.
is in the direction of motion, the particle will accelerate or the speed will increase.
And  , it shows the time rate of change of the direction of the velocity. Hence,
, it shows the time rate of change of the direction of the velocity. Hence,  is in the positive n direction always, i.e. towards the center of curvature.
is in the positive n direction always, i.e. towards the center of curvature.
This is the reason why, 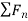 is referred as the centripetal force.
is referred as the centripetal force.